XGBoost算法在多光谱遥感浅海水深反演中的应用

胡 鹏, 赵露露, 高 磊, 朱金山, 2, 3

XGBoost算法在多光谱遥感浅海水深反演中的应用

胡 鹏1, 赵露露1, 高 磊1, 朱金山1, 2, 3

(1. 山东科技大学测绘科学与工程学院, 山东 青岛 266590; 2. 地理信息工程国家重点实验室, 陕西 西安 710054; 3. 自然资源部海洋测绘技术重点实验室, 山东 青岛 266590)

在多光谱遥感浅海水深反演过程中, 考虑到水体和底质影响, 水深值和海水表面辐射亮度之间的线性关系不成立。本文以甘泉岛南部0~25 m范围的沙质区域为研究区域, 利用GeoEye-1多光谱遥感影像和多波束实测水深数据构建XGBoost非线性水深反演模型, 研究了XGBoost算法用于水深反演的性能。以决定系数(2), 均方误差(MSE)和平均绝对误差(MAE)作为评价指标, 并与3种传统线性回归模型进行了对比分析。结果表明, XGBoost非线性水深反演模型的2、MSE和MAE分别为0.991、0.33 m和0.44 m, 拟合程度最好, 精度优于线性回归模型。为进一步探究各模型在不同水深的反演精度, 将水深范围分成3段(0~8 m, 8~15 m, 15~25 m)分别进行精度验证和误差分析。结果表明, XGBoost模型在各分段的精度均优于线性回归模型, MSE依次为0.56 m, 0.14 m和0.43 m。可见, 在单一底质区域下XGBoost模型的水深反演精度更高, 且反演效果更稳定。

光学浅海水深反演; XGBoost算法; 非线性回归模型; 底质类型

我国海岸线漫长、海域辽阔, 拥有丰富的优势海洋资源, 水深信息探测对海上交通运输、海洋科学研究及海岸带规划管理等具有重要意义[1-2]。浅海水深信息作为海岛礁、海岸带重要的地形数据, 时常受海上天气变化、海底地形复杂多样、时空限制、经费不足以及权益争端海域难以进入等影响, 水深信息现场探测工作难以开展[3]。

20世纪60年代多光谱遥感卫星升空, 为水深反演模型提供了多光谱遥感数据, 光学水深遥感技术得到了迅速发展, 迄今为止常用的浅海水深反演模型主要有理论解析模型、半理论半经验模型和统计模型三类[4]。

Figueiredo等对Lyzenga利用双层流近似假设建立的理论解析模型进行了改进[5-8]。理论解析模型精度高, 但实际应用受到众多水体光学参数难以获取的限制。Su等[9]在Paredes等[10]和Stumpf等[11]建立的对数线性模型基础上, 结合克里金插值建立了克里金反演水深模型。半理论半经验模型在保证了反演精度的前提下, 减少了模型参数的输入量和计算量。

王艳姣等利用Landsat7 ETM+影像和实测水深数据, 建立了动量BP人工神经网络模型反演水深信息[12]。邱耀炜等结合随机森林算法构建了甘泉岛海域的非线性水深反演模型[13]。朱金山等针对海底底质不均一情况, 提出了一种结合底质分类与SVR算法的水深反演模型[14]。考虑到实际海底底质并不均一, 不同海底底质类型建立不同水深反演模型十分必要。

有学者以海水波为切入点研究水深遥感, Adrien等提出了一种利用小波和互相关技术及线性色散关系进行SPOT-5立体像对水深反演的方法[15]。Li等利用QuickBird高分辨率遥感影像提出了海浪谱测深反演方法[16]。目前XGBoost算法针对于光学浅海水深反演的应用较少。

本文以南海甘泉岛南部海域为研究区域, 利用GeoEye-1多光谱遥感数据和多波束实测水深数据对沙质底质区域构建XGBoost水深反演模型。以决定系数(2), 均方误差(MSE)和平均绝对误差(MAE)作为评价指标, 用实测水深样点验证XGBoost模型精度, 并同单因子、双因子和多因子回归模型进行对比分析。进一步探究在不同水深范围, XGBoost算法在沙质底质区域反演水深的性能。

1 XGBoost原理

极限梯度提升算法, 即XGBoost(eXtreme Gradient Boosting)算法, 可用于解决非线性回归问题。它由陈天奇提出设计, 致力于让提升树突破自身的计算极限, 以实现运算快速, 性能优秀的工程目标[17]。与传统的梯度提升算法相比, XGBoost进行了许多改进, 它能够比其他使用梯度提升的集成算法更加快速, 并被广大学者认为是在分类和回归上都拥有超高性能的先进评估器。

XGBoost与决策树、SVM等算法不同, 其核心是基于梯度提升树实现的集成算法, 整体来说可以有三个核心部分: 集成算法本身, 用于集成的弱评估器, 以及应用中的其他过程。XGBoost建模过程大致如下: 首先使用训练集建立一棵树, 然后用这棵树预测训练集, 每次迭代过程中都会增加一棵树来拟合上次预测的残差, 逐渐形成由众多树模型集成的强评估器, 各个叶子权重之和便是该样本的预测值。XGBoost在传统损失函数的基础上引入了模型复杂度来衡量算法的运算效率, 其目标函数为:

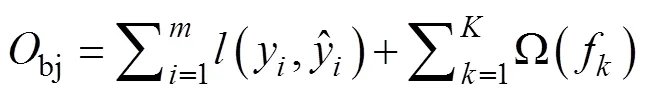
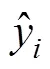
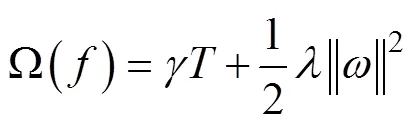
2 水深反演模型建立

2.1 研究区域与数据处理

本文选取西沙群岛中的甘泉岛南部海域作为研究区域, 如图1a中红色框所示, 其经纬度范围为16°29′55″N~16°30′17″N, 111°34′21″E~111°35′26″E。遥感影像为2013年2月18日获取的GeoEye-1多光谱影像, 具有蓝、绿、红和近红外四个标准波段, 空间分辨率为2 m, WGS-84坐标系。

为了进行水深信息定量提取, 采用ENVI软件对GeoEye-1影像进行辐射定标、FLAASH大气校正和NDWI水陆分离等预处理。实测水深数据信息由DL-V3惯导接收机和R2Sonic 2024多波束测深仪采集, 其水平精度为0.2 m, 量程分辨率为1.25 cm, 采用CGCS2000国家大地坐标系。由于遥感影像成像和水深数据采集存在时间差, 本文采用中国海事服务网(https://www. cnss.com.cn/tide/)提供的潮位信息进行潮汐校正。

为挑选单一底质作为研究区域, 本实验中采用支持向量机(SVM)进行底质分类。SVM基于统计学习理论, 具有自动找出区分地物类别较强支持向量的能力, 并具有较高的分类准确率[18]。通过遥感影像目视解译和水下视频辨析选取沙质底质的像元作为SVM分类训练样本, 并将分类后结果进行矢量化输出, 结果如图1b所示。为了实现遥感影像与水深数据精确配准, 需要将遥感影像坐标系转换为水深数据坐标系(CGCS2000), 配准后结果如图1c所示。

2.2 线性回归模型

根据配准后水深点数据的经纬度坐标, 将遥感影像对应位置的4个波段像元值分别提取到水深范围在0~25 m的921个水深数据点上。将水深数据点按8︰2比例随机划分, 其中训练样本点736个, 测试样本点185个。为了挑选合适的模型反演参数, 统计736个水深点值与GeoEye-1影像4个波段及6个波段组合的相关性如表1所示。根据表1, 选取1/2、4/2和4/3三个相关性强的反演因子, 分别组建单因子、双因子和多因子线性回归模型, 见表2。

2.3 XGBoost模型

太阳耀斑、水体类型、水体悬浮物质和海底底质等都会导致水深值和海水表面辐射亮度之间的线性关系并不成立, 从而影响模型反演精度。XGBoost采用多颗CART树进行预测, 泛化性能好, 非常适合解决复杂的非线性回归问题。采用与线性模型相同的训练样本, 构建XGBoost水深反演模型。根据表1中各因子相关系数, 选取4个波段(1、2、3、4)和6个波段组合信息(1/2、3/1、4/1、3/2、4/2、4/3)作为输入特征, 实测水深信息作为输入标签。

图1 研究区域及样本点分布情况

表1 水深值与GeoEye-1影像各波段及波段组合的决定系数

因子B3/B1B4/B1B3/B2B4/B2B4/B3 决定系数R20.3670.6680.1380.8050.702

表2 线性回归模型

计算模型中各个特征的重要性, 图2反映了10个特征对模型的贡献, 重要性值越大说明该特征与标签信息最密切。在10个特征中1/2重要性分数最高, 说明该特征对模型的影响最大。

构建XGBoost模型过程中, 训练集和测试集的划分会干扰模型的结果。使用K折交叉验证(K-Fold Cross Validation)能够观察模型的稳定性, 有效避免信息泄露对模型超参数的影响。交叉验证是将数据划分为K份, 依次使用其中一份作为测试集, 其他K– 1份作为训练集, 多次计算模型的精度来评估模型的平均精度。将网格搜索与学习曲线结合, 通过多次试验对模型进行优化调参, 参数取值如表3所示, 其他参数缺省。

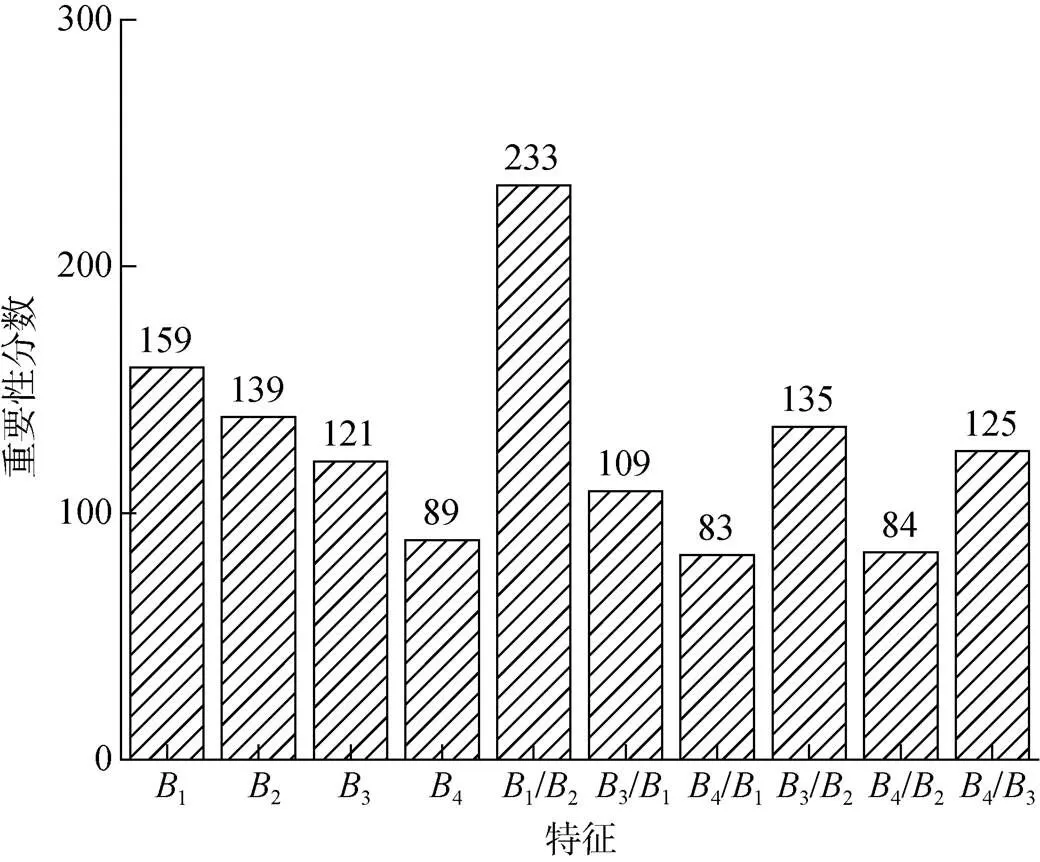
图2 特征重要性分数

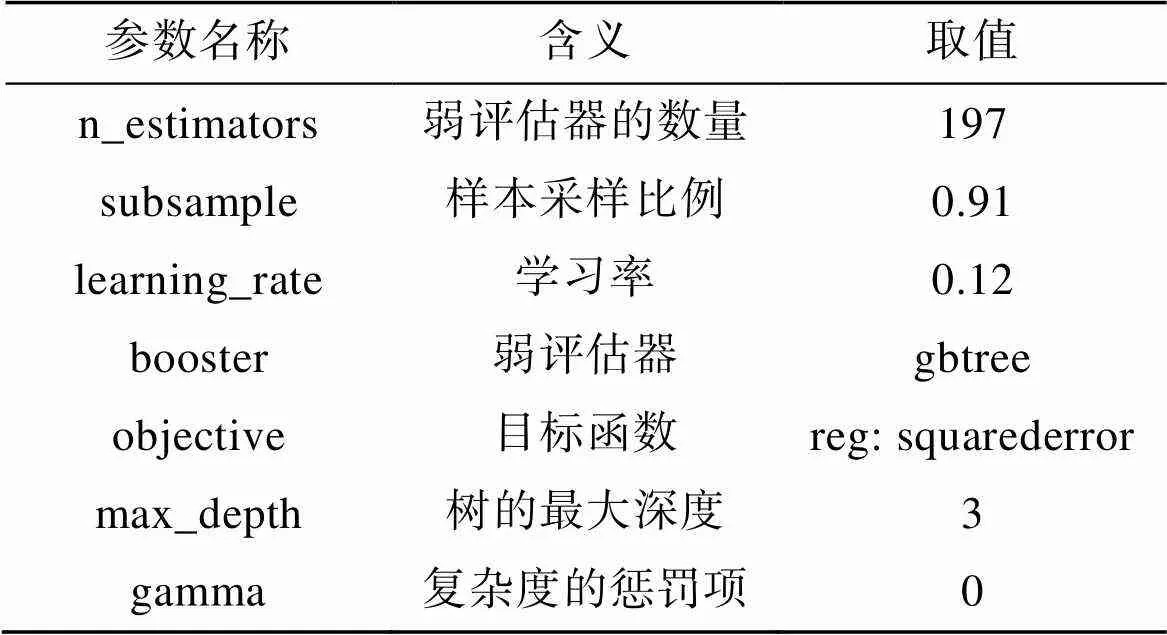
表3 模型重要参数取值

采用5折交叉验证绘制模型调参后在不同训练样本上的学习曲线, 来衡量模型反演水深的性能, 结果如图3所示。图3中随着训练样本数量增加, XGBoost模型的过拟合逐渐减轻, 泛化能力逐渐提高, 训练集和测试集的结果逐渐接近。

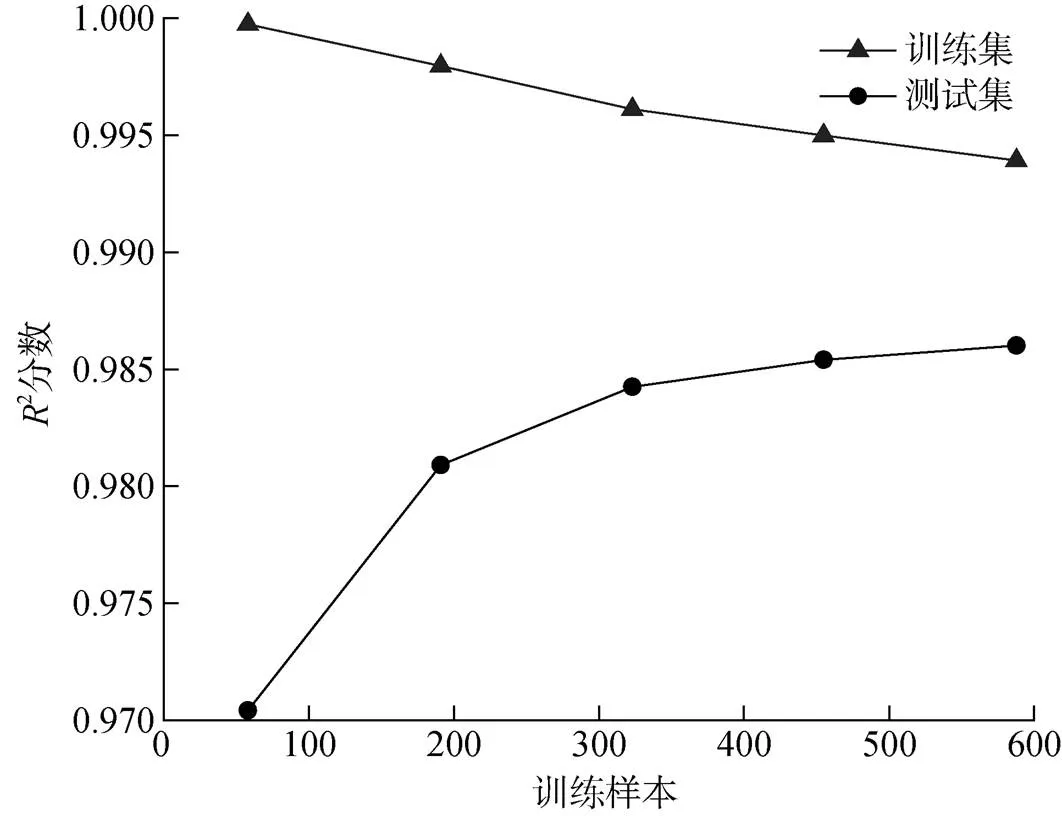
图3 XGBoost学习曲线

3 结果与分析

为了检验XGBoost模型水深反演能力, 以未参与建模的185个实测水深点作为验证样本, 并同线性回归模型反演的水深值与水深实测值之间的误差进行对比分析。采用决定系数(2)、均方误差(MSE)和平均绝对误差(MAE)作为精度评价指标, 并绘制了各模型得到的水深反演值与实测值分布散点图, 结果如图4所示。图4直观反映了各模型反演水深值和实测水深值的偏离程度, 各验证样本点离图中1︰1直线越接近说明离散程度越小, 反演结果越可靠, 模型具有较高精度。

在3种线性模型中, 单因子模型(图4a)总体偏移量较大, 精度最低, 均方误差(MSE)和平均绝对误差(MAE)为1.52 m和0.91 m, 多因子模型(图4c)精度最高, MSE和MAE分别为0.58 m和0.59 m, 说明多因子线性模型结合多个波段信息后反演精度得到提高。XGBoost模型偏差明显较小,2、MSE和MAE精度均优于线性回归模型, 分别为0.991 m、0.33 m和0.44 m。

从总体上看, 4个水深反演模型的决定系数(2)均在0.95以上, 说明各模型的自变量与因变量均表现为强相关性。其中XGBoost模型性能最优, 说明XGBoost模型综合利用10个特征信息后, 在其非线性回归预测能力支撑下, 取得了较好的反演精度。

为进一步分析各模型水深反演能力, 将水深范围分成3段(0~8 m, 8~15 m, 15~25 m), 分段比较分析XGBoost模型与其他三种线性回归模型的精度, 结果如表4所示。从表4和图4可以看出, 在8~15 m段XGBoost模型和线性模型的水深反演值与实测值偏离程度最小, 拟合程度最好, 各模型精度也优于其他水深范围。其中XGBoost模型的精度最高, MSE为0.14 m。在15~25 m段, 单因子模型(图4a)离散程度较大, MSE高达2.59 m, 反演值整体偏低, 可能是此模型只包含了蓝绿波段, 而没有考虑到其他波段信息, 从而限制了其水深反演能力。在0~8 m段, 各模型拟合效果较差, 可能是该段的底质较复杂混合像元较多, 导致SVM分类结果较差, 水深反演时受其他底质类型影响。特别是2 m左右浅水区处于波浪破碎带, 易受白色浪花干扰, 在一定程度上影响了反演结果。但是对于任意分段, 综合利用多个波段特征信息的XGBoost模型的反演精度均优于线性回归模型。

总体来说, XGBoost模型获得的水深反演值与实测值之间的2最高、MSE和MAE最低, 结果表明采用XGBoost非线性模型进行水深反演可取得较好的结果。

4 结束语

本文基于水深实测数据和GeoEye-1多光谱遥感影像, 构建XGBoost非线性回归预测模型对甘泉岛南部0~25 m水深范围内沙质区域进行水深定量反演, 并同3种线性回归模型进行精度对比分析。结果分析表明: 模型中包含波段特征信息的个数在一定程度上影响反演精度, 对于任意分段, 综合多个波段信息构建的XGBoost模型的反演精度均优于线性回归模型。由此可见, XGBoost非线性模型更适合反演甘泉岛南部沙质海域。

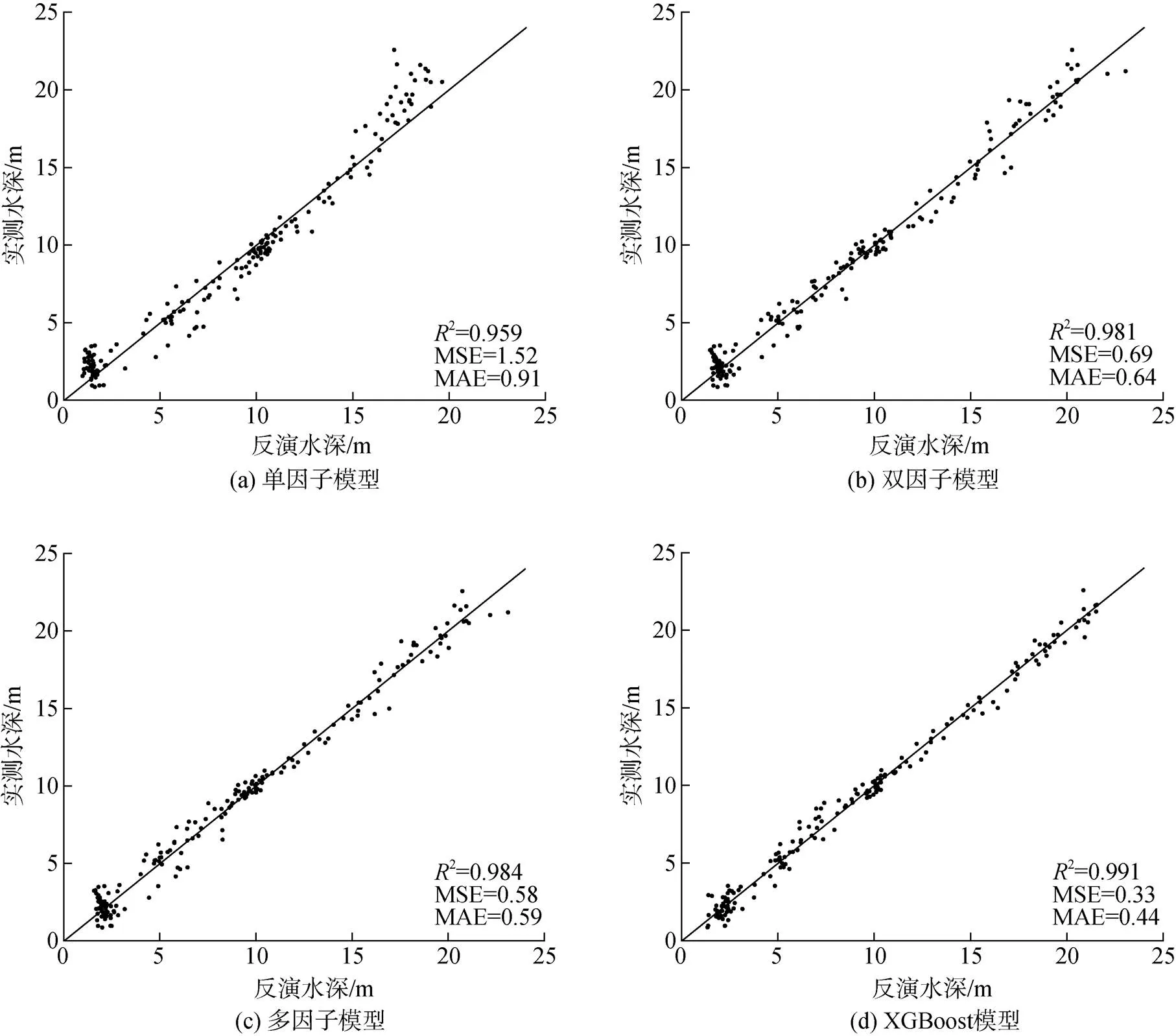
图4 水深反演值与实测值散点图

表4 各模型水深反演结果分段比较

本文的研究工作仍存在不足之处, 在构建各模型时, 研究范围只针对海底底质类型为沙子的区域, 未对其他底质类型区域展开研究。在前期使用SVM分类器进行单一底质分类时, 0~8 m段沙子和其他底质类型混合较为严重, 导致该分段范围受混合像元影响较大, 误将其他底质类型分入沙子类型, 从而影响反演精度。选取空间分辨率较高和光谱波段范围较宽的遥感影像在一定程度上能提高SVM分类精度和水深反演精度。

[1] 王晶晶, 田庆久. 海岸带浅海水深高光谱遥感反演方法研究[J]. 地理科学, 2007(6): 109-114.WANG Jingjing, TIAN Qingjiu. Study on inversion method of deep hyperspectral remote sensing for coastal shallow water[J]. Geographic Science, 2007(6): 109-114.

[2] 张鹰, 张芸, 张东, 等. 南黄海辐射沙脊群海域的水深遥感[J]. 海洋学报, 2009, 31(3): 39-45. ZHANG Ying, ZHANG Yun, ZHANG Dong, et al. Remote sensing of water depth in the radial sand ridges of the South Yellow Sea[J]. Acta Oceanographica Sinica, 2009, 31(3): 39-45.

[3] 王艳姣, 董文杰, 张培群, 等. 水深可见光遥感方法研究进展[J]. 海洋通报, 2007(5): 93-102. WANG Yanjiao, DONG Wenjie, ZHANG Peiqun, et al. Research progress of water depth visible light remote sensing method[J]. Ocean bulletin, 2007(5): 93-102.

[4] 马毅, 张杰, 张靖宇, 等. 浅海水深光学遥感研究进展[J]. 海洋科学进展, 2018, 36(3): 5-25. MA Yi, ZHANG Jie, ZHANG Jingyu, et al. Progress in optical remote sensing of shallow water depth[J]. Progress in Marine Science, 2018, 36(3): 5-25.

[5] LYZENGA D R. Passive remote-sensing techniques for mapping water depth and bottom features[J]. Applied Optics, 1978, 17(3): 379-383.

[6] FIGUEIREDO I N, PINTO L, GONÇALVES G. A modified Lyzenga’s model for multispectral bathymetry using Tikhonov regularization[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 13(1): 53-57.

[7] LYZENGA D R. Shallow-water bathymetry using combined lidar and passive multispectral scanner data[J]. International Journal of Remote Sensing, 1985, 6(1): 115- 125.

[8] LYZENGA D R, MALINAS N P, TANIS F J. Multispectral bathymetry using a simple physically based algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(8): 2251-2259.

[9] SU H, LIU H, WU Q. Prediction of water depth from multispectral satellite imagery—The regression kriging alternative[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(12): 2511-2515.

[10] PAREDES J M, SPERO R E. Water depth mapping from passive remote sensing data under a generalized ratio assumption[J]. Applied Optics, 1983, 22(8): 1134- 1135.

[11] STUMPF R P, Holderied K, Sinclair M. Determination of water depth with high-resolution satellite imagery over variable bottom types[J]. Limnology and Oceanography, 2003, 48(1): 547-556.

[12] 王艳姣, 张鹰. 基于BP人工神经网络的水体遥感测深方法研究[J]. 海洋工程, 2005, 23(4): 33-38.WANG Yanjiao, ZHANG Ying. Research on water remo­te sensing sounding method based on BP artificial neural network[J]. Ocean Engineering, 2005, 23(4): 33-38.

[13] 邱耀炜, 沈蔚, 惠笑, 等. 基于WorldView-2数据和随机森林算法的遥感水深反演[J]. 遥感信息, 2019, 34(2): 78-82.QIU Yaowei, SHEN Wei, HUI Xiao, et al. Remote sensing water depth retrieval based on worldview-2 data and random forest algorithm[J]. Remote Sensing Information, 2019, 34 (2): 78-82.

[14] 朱金山, 宋珍珍, 赵露露. 结合底质分类与SVR算法的多光谱影像测深[J]. 地理空间信息, 2019, 11: 44-46.ZHU Jinshan, SONG Zhenzhen, ZHAO Lulu. Multispectral image bathymetry combined with sediment clas­sification and SVR algorithm[J]. Geospatial Information, 2019, 11: 44-46.

[15] POUPARDIN A, IDIER D, DE MICHELE M, et al. Water depth inversion from a single SPOT-5 dataset[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 54(4): 2329-2342.

[16] LI J, ZHANG H, HOU P, et al. Mapping the bathymetry of shallow coastal water using single-frame fine-resolution optical remote sensing imagery[J]. Acta Oceanologica Sinica, 2016, 35(1): 60-66.

[17] CHEN T, GUESTRIN C. Xgboost: A scalable tree boosting system[C]//ACM SIGKDD International Con­ference on Knowledge Discovery and Data Mining ACM. San Francisico: CA, 2016: 785-794.

[18] 闫琰, 董秀兰, 李燕. 基于ENVI的遥感图像监督分类方法比较研究[J]. 北京测绘, 2011(3): 14-16. YAN Yan, DONG Xiulan, LI Yan. Comparative study on supervised classification methods of remote sensing image based on envi[J]. Beijing Surveying and Mapping, 2011(3): 14-16.

Application of XGBoost algorithm on multispectral shallow water bathymetry retrieval

HU Peng1, ZHAO Lu-lu1, GAO Lei1, ZHU Jin-shan1, 2, 3

(1. Geomatics College, Shandong University of Science and Technology, Qingdao 266590, China; 2. State Key Laboratory of Geographic Information Engineering, Xi’an 710054, China; 3. Key Laboratory of Marine Mapping Technology, Ministry of Natural Resources, Qingdao 266590, China)

In optical shallow water bathymetry retrieval, due to the influence of the water and sediment types, the relationship between the water depth and sea surface reflectance is nonlinear. In this study, we built a nonlinear depth inversion model that uses the XGBoost algorithm. The research area was a 0–25 m sandy area around Ganquan Island in the South China Sea. GeoEye-1 multispectral data and in-situ multibeam data were used to investigate the depth inversion performance of the XGBoost algorithm. To evaluate the retrieved bathymetry results, we calculated the correlation coefficient (2), mean square error (MSE), and mean absolute error (MAE) values. We then compared the XGBoost bathymetry results with those of three linear regression models, and found the XGBoost nonlinear depth inversion model to have the best fitting performance and better precision, with2, MSE and MAE values of 0.991, 0.33, and 0.44 m, respectively. To further explore the performance of each model at different depths, we divided the water depth into three ranges (0–8 m, 8–15 m, 15–25 m). The results show that, in each depth range, the XGBoost model’s accuracy was better than those of the linear regression models. The MSE values in each depth range are 0.56, 0.14, and 0.43 m, respectively. Based on these results, we can conclude that, compared to other models, the depth inversion accuracy of the XGBoost model is higher, and its inversion effect is more stable in a single sediment region.

optical shallow water depth inversion; XGBoost algorithm; nonlinear regression model; sediment type

Dec. 26, 2019

P237

A

1000-3096(2021)04-0083-07

10.11759/hykx20191226002

2019-12-26;

2020-01-09

地理信息工程国家重点实验室开放研究基金资助项目(SKLGIE2017-Z-3-3); 国家重点研发计划课题(协作)-极区海域水声环境观测与声场特性研究(2018YFC1405903); 测绘地理信息公益性行业科研专项(201512034)

[Project Supported by Open Research Foundation of National Key Laboratory of Geographic Information Engineering, No. SKLGIE2017-Z-3-3; National Key Research and Development Project (Cooperation) - Underwater Acoustic Environment Observation and Sound Field Characteristics in Polar Waters, No. 2018YFC1405903; Special Scientific Research Project of Surveying and Mapping Geographic Information Public Welfare Industry, No. 201512034]

胡鹏(1996—), 男, 湖南湘潭人, 硕士研究生, 研究方向为海洋遥感, E-mail: hupeng_1996@163.com; 朱金山(1974—),通信作者, E-mail: zhujinshan@sdust.edu.cn, 电话: 0532-86057276

(本文编辑: 杨 悦)