基于DDPG的光储微电网系统能量决策优化
2021-05-27李华,于潇
李 华,于 潇
(1.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津300132;2.河北省电磁场与电器可靠性重点实验室(河北工业大学),天津300132)
0 引言
近年来,国家对分布式发电的扶持力度不断加大,屋顶分布式光伏发电成为了许多家庭的有效选择。而光电本身的不确定性会造成一定程度的弃光现象,给公共电网的稳定运行带来很大的挑战[1]。为此,在新能源消纳困难的地区要提高光电的就近消纳能力,充分挖掘现有系统的调峰能力[2]。储能技术的引入不仅能够提升分布式光伏的就地消纳能力,还可以提升系统稳定性,改善电能质量,将系统由“刚性”变为“柔性”[3],[4]。
针对微电网中的能量管理和优化控制问题,文献[5]利用粒子群优化算法寻求储能电站调度任务的最优分配方案,最大限度地降低了调度成本。文献[6]提出了一种集成混合整数线性规划、多尺度规划和基于优先级的模糊随机规划算法,这些算法能够解决微电网中的许多问题。文献[7]构造了包含蓄电池和储氢装置的微电网复合储能模型,采用DQN(Deep Q Network)算法对微电网系统的能量调度进行决策优化。文献[8]采用Q学习算法研究了以风储合作系统长期收益最大化为目标的风储合作系统参与电力交易的能量调度优化问题,并考虑了申购的备用容量成本。文献[9]采用强化学习算法,使电源、分布式存储系统和用户在互相没有先验信息的情况下能够达到纳什均衡。
针对微电网中储能设备的管理问题,本文以家庭光储系统的累计经济收益和蓄电池调节能力为目标,设计了一种基于深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)的光储微电网系统能量调度方法。首先阐述了理论基础和数学模型,然后通过历史数据和探索性策略进行网络参数的训练,最后对比和分析了不同奖励函数下系统的年收益,验证了以长期收益最大为目标的小型家庭式光储系统能量调度策略的有效性和可行性。
1 深度确定性策略梯度
1.1 算法基础
强化学习作为机器学习的一个分支,其原理为智能体在通过与环境的不断交互的过程中得到环境的反馈奖励,然后根据反馈奖励对动作进行评估和改进,以使评估越来越准、采取的动作越来越好。强化学习的理论基础是马尔科夫决策过程(Markov Decision Process,MDP),MDP可以用一个五元组(S,A,P,R,γ)来表示,其中,S为状态集,A为动作集,P为转移概率,R为奖励函数,γ为折扣因子。t时刻,在策略π下,智能体根据当前状态st采取动作at,并依据转移概率p(st+1|st,at)进入到下一个状态st+1,同时得到来自环境的反馈rt。为降低未来反馈对当前的影响,须将γ与回报函数r相乘来计算累计回报Rt。

强化学习的目标是找到最佳策略π,得到累计回报期望的最大值。为了便于求解,须对某一时刻的状态动作进行评估,为此引入了状态动作值函数的概念,表达式如下:

利用基于蒙特卡罗的强化学习方法、基于时间差分的强化学习方法和基于值函数逼近的强化学习方法,对状态动作值函数进行求解。其中,前两个方法难以解决状态空间和动作空间较大的问题,在基于值函数的强化学习方法中,DDPG算法在处理高维连续动作空间问题时有良好的表现。
1.2 算法原理
DDPG是强化学习算法的一个重要里程碑,其中深度神经网络的应用增强了模型的特征提取能力,为强化学习在高维连续状态空间的应用提供了可能。同时,DDPG算法继承了DQN算法中的经验回放和独立目标网络,旨在打破数据之间的关联性,降低模型的训练难度。与DQN算法相比,DDPG算法使用了演员-评论家(Actor-Critic Algorithm,AC)网络,使动作空间也升级为连续。DDPG算法更新网络参数如式(3)~(7)所示。


DDPG算法避开了传统启发式算法在解决微电网能量管理和调度上的局限,它不需要研究者制定具体的决策流程和目标函数,代之以动作空间、状态空间、奖励函数和一定的变量约束就可以将初始网络训练成想要的网络。系统的预测和能量调度在该算法下可实时进行,电能交易规则根据奖励函数值实时更新,具有自发滚动协调不同时间尺度的功能。与随机策略相比,确定性策略对采样数量要求低,在处理高维动作空间的问题时计算速度更快。
2 数学模型
2.1 源-网-储-荷场景构建
如图1所示,家庭光储一体化模型为源-网-储-荷的家庭微电网系统,包括交直流母线、光伏组件、公共电网、蓄电池、变流器以及由直流负载和交流负载组成的家庭用电负荷,箭头代表功率流向。其中光伏组件将太阳能转换为电能,供给交流负荷或经过变流器将电能转换成直流电供给直流负载或蓄电池。用户是光储一体化系统的直接收益者,当光伏发电量和蓄电池存储电能不足以供给本地负荷使用时,用户从公共电网购电;当光伏发电量或蓄电池存储电能盈余时,用户可以选择出售给电网获取收益或存储备用。

图1 光储系统合作机制Fig.1 Hybrid system cooperationmechanism
2.2 光伏组件出力模型
光伏发电系统的出力模型为
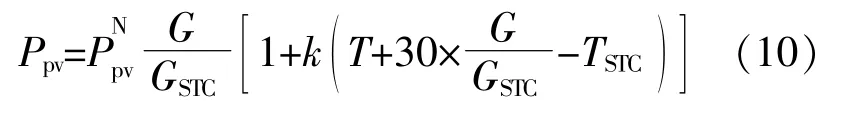

2.3 蓄电池充放电模型
蓄电池的充、放电模型分别为

2.4 合作机制及约束


2.5 空间及奖励函数
2.5.1 状态空间和动作空间
家庭式光储系统的状态空间s:{m,sbat,Ppv-Pl},其中:m包含24个状态,代表了从开始到之后24 h每个时段的电价,分别为m(t),m(t+1),…,m(t+23);sbat为蓄电池的剩余电量;Ppv-Pl为光伏发电系统供给家庭用电负荷后的剩余电量。动作空间A:{pbat},其中:pbat>0蓄电池放电;pbat<0蓄电池充电;pbat=0蓄电池闲置,既不充电也不放电。
2.5.2 奖励函数
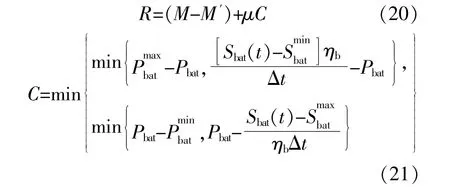
式中:R为累计收益;M-M'为光储一体化系统比采用“自发自用,余电上网”模型的系统多出的盈利额,它保证了系统的累计收益和功率平衡;μ为蓄电池调节能力的奖励系数;C为蓄电池的调节能力。
μ反映了蓄电池调节能力的重要程度,是系统自身盈利与系统功率波动平衡之间的平衡度量。μ的取值越小,经训练后的模型盈利能力越强;μ的取值越大,经训练后的模型平抑功率波动能力越强。经多次实验分析对比,得到较为理想的μ值,在该μ值下,系统的自身盈利与系统功率波动平衡之间达到博弈均衡。
3 学习步骤
本实验中所用的AC网络架构如图2所示。为了使模型响应不同时间的电价,在Actor网络中,s1先经过两个卷积池化块,每个卷积池化块包含一个卷积核尺寸为15的卷积层和一个尺寸为2的最大池化层,连接层将其与s2连接为一个变量;之后经过4个全连接层,其中,前3个全连接层的激活函数为relu,最后一个全连接层通过
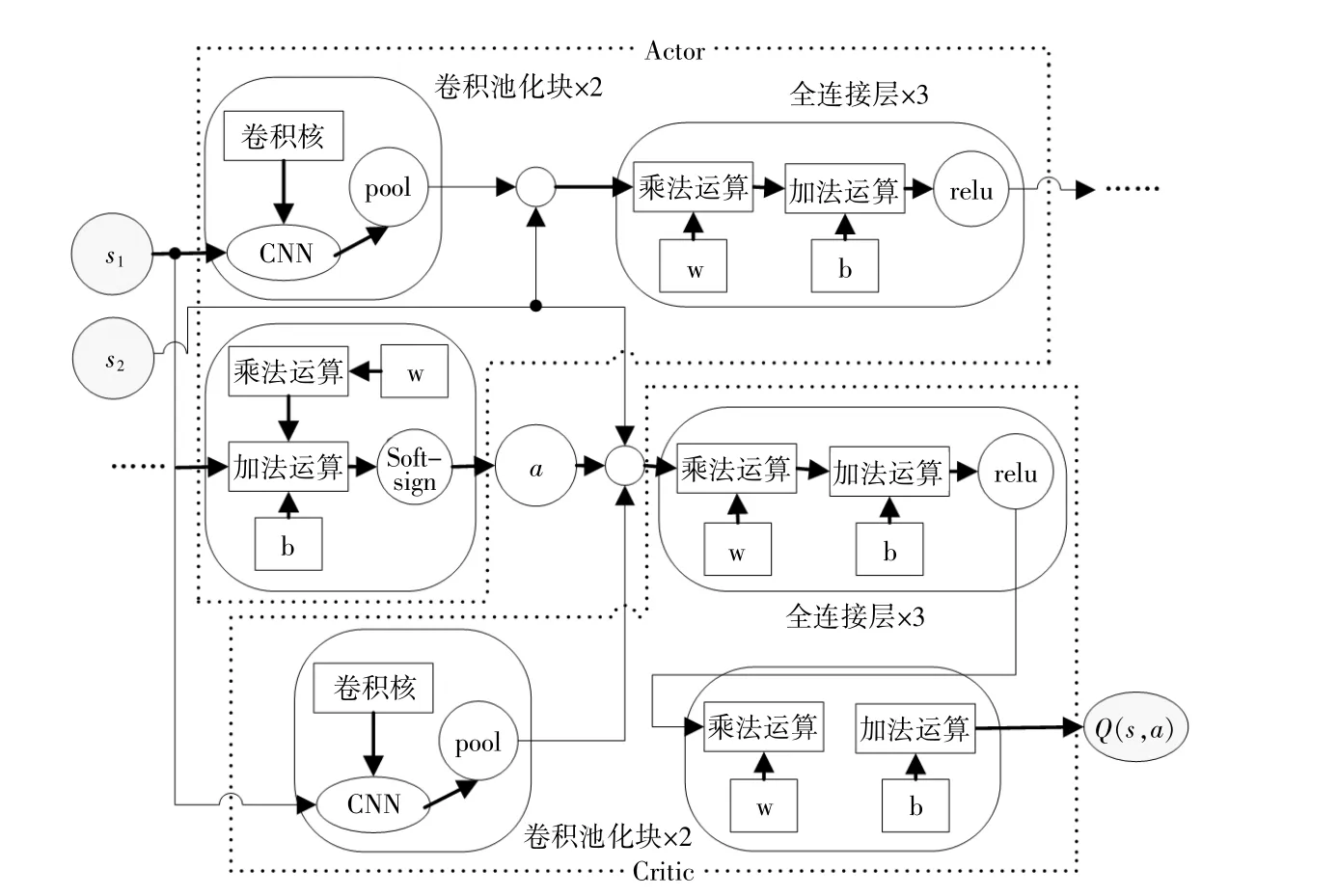
图2 网络架构图Fig.2 Network architecture diagram
softsign激活函数得到动作a。在Critic网络中,s1先经过两个卷积池化块,连接层将其与动作a和s2连接成一个变量输入到一个激活函数为relu的全连接层中,之后再经过一个无激活函数的全连接层得到Q(s,a)。该网络的具体训练步骤如图3所示。
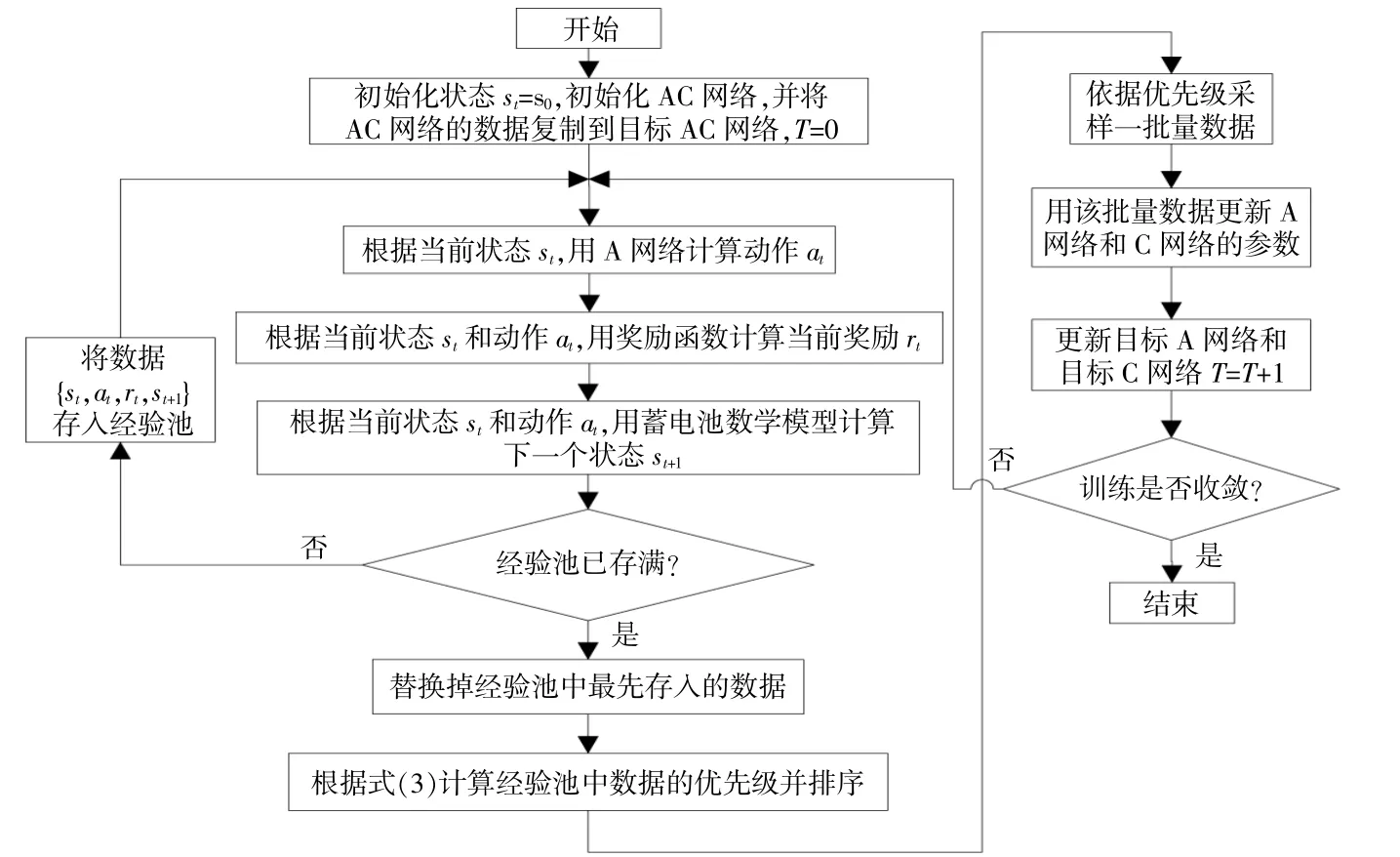
图3 DDPG训练流程图Fig.3 DDPG training flowchart
4 算例分析
4.1 基础数据


表1 日分时电价Table 1 Time-of-use power price
在本文所建立的家庭光储微电网模型中,采用时间跨度为1 a的实验数据进行了多次实验,将光伏发电所需的气象数据、负荷数据与分时电价信息作为输入数据,蓄电池动作作为输出数据。为使结果更加清晰直观,下文将用蓄电池剩余电量、微电网-公共电网联络线上的功率波动和系统年收益加以表示。
4.2 实验结果对比
图4为损失值变化趋势曲线,其中,loss1为C网络的损失值,loss2为A网络的损失值。从图中可以看出,随着训练次数的增加,损失值逐渐接近0,说明训练效果趋于稳定,模型趋于收敛。
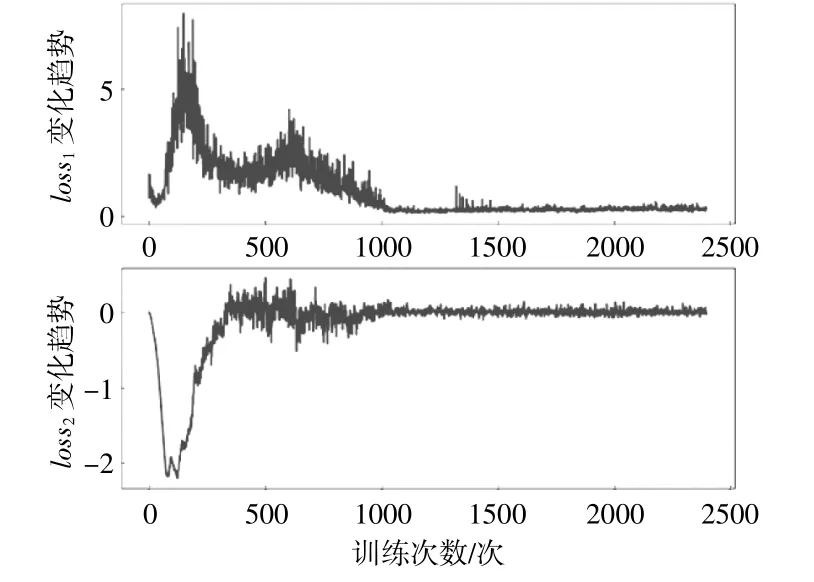
图4 损失值变化趋势曲线Fig.4 Trend curve of loss value
图5为截取了时长为1 d的蓄电池剩余电量变化趋势曲线。从图中可以看出:当μ=0.1时,经训练后的模型以系统最大年收益为主要目标,高电价时蓄电池迅速放电至容量下限,低电价时蓄电池迅速充电至容量上限,且蓄电池剩余电量达到容量上限和容量下限的状态持续了很长时间,在此期间,蓄电池始终没有调节能力;当μ=0.2时,蓄电池剩余电量停留在容量上限和容量下限的时间变短;当μ=0.3时,蓄电池剩余电量停留在容量上限和容量下限的时间为0,说明在第8小时以外的时段蓄电池均保留了调节能力,在第13小时,蓄电池的工况由放电转为充电,说明其具备感知平时段和峰时段之间微小电价差的能力,在后面的峰时段电价到来之际,蓄电池开始放电以套取更多收益;当μ=0.4时,蓄电池剩余电量曲线接近于一条水平直线,说明此时经训练后的模型以蓄电池调节能力为主要目标,盈利意愿不明显。
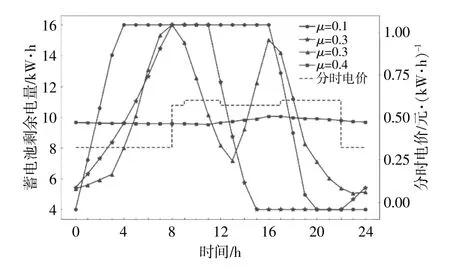
图5 蓄电池剩余电量曲线图Fig.5 Curve of battery remaining power
在实际运行过程中,由于光伏发电的波动性,光伏系统出力的实际值与预测值存在一定的偏差,这会导致源-储-荷系统与公共电网间的联络线上的功率波动较大,而有调节能力的蓄电池可以在一定程度上平抑联络线上的功率波动,其平抑功率波动能力的强弱取决于奖励函数中μ值的大小。图6为截取了800 h内,μ分别取0.1,0.2,0.3和0.4时联络线上的功率波动情况。从图中可以看出,μ的取值越大,联络线上的功率波动越小,说明蓄电池平抑功率波动的能力越强,系统向电网申购备用容量的成本越低。
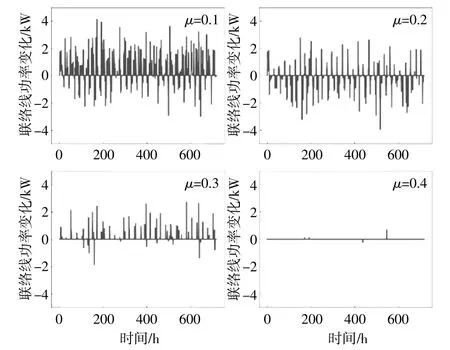
图6 联络线上的功率波动曲线Fig.6 Curve of power fluctuations on the Power tie line
表2给出了不同模型下家庭光储微网系统的年支出与年收益对比,年支出为系统用电成本,年收益为系统利用电价差进行低电价买入电能、高电价卖出电能挣得的额外收益。其中“自发自用”模型即采用“自发自用,余电上网”政策的模型。从表中可以看出,在家庭光储微电网模型中,当μ=0.2和μ=0.3时,系统的年收益较多,且这两种情况下的系统年收益差别不大。
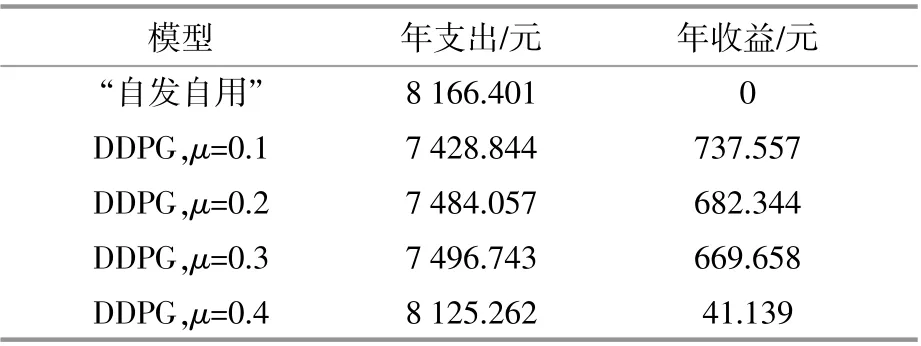
表2 不同模型下的年支出与年收益Table 2 Annual expenditure and annual income under differentmodels
综上所述,当μ=0.3时,家庭光储微电网系统中的蓄电池调节能力较强,同时也可以很好地响应电价激励。说明此时,该模型并没有以牺牲很多年收益为代价来提高蓄电池对联络线上功率波动的平抑能力,反而维持在较高的年收益水平,同时对电网负荷侧也起到了削峰填谷的作用。
5 结论
本文将深度强化学习理论引入源-网-储-荷的家庭光储一体化微电网系统中,计算系统中蓄电池的充放电功率,其结果具有很强的自洽性。将DDPG算法应用于家庭光储微电网系统的能量决策优化问题中,有效地改善了系统的灵活性、实时性和经济性,提升了系统平抑功率偏差的能力。
