双臂机器人的轨迹规划研究与仿真1
2021-05-26刘子贵
刘子贵
(江门职业技术学院 广东省江门市 529090)
0 引言
工业机器人能够代替人工完成枯燥、重复性较高的工作,大幅提高生产效率,甚至可以完成一些人工无法完成的危险性任务。虽然单臂机器人已经得到了广泛应用,但随着生产作业越来越复杂,单臂机器人在某些场合下已经无法胜任,例如较为复杂的搬运、柔性装配等应用,而双臂机器人则能完成这些工作任务。因此,研究双臂机器人的运动轨迹规划,可以提高机器人的双臂协作、协调能力,扩展其应用领域[1]。
1 轨迹规划方法
关节变量空间轨迹规划的常见方法有三次多项式插值和五阶多项式插值等方法。在关节变量空间中研究双臂机器人的轨迹规划,需要先根据机器人的逆运动学方程,算出机器人末端在运动轨迹上各个点的关节变量值,再利用这些关节变量值拟合出每个关节的运动轨迹。最后必须要保证运动轨迹、速度曲线、加速度曲线的连续性,以达到机器人运动平稳的目标[2]。
1.1 三次多项式插值法
设已知机器人的起点和终点位姿,根据机器人逆运动学方程,求出每个关节在初始时刻t0的关节值为θ0,终止时刻tf的关节值为θf。为了保证关节运动速度的平稳性,设定起点和终点的关节角速度为0,即:。根据这4个约束条件,可以确定该关节变量的三次多项式表达式,即:

对公式1求一阶和二阶导数,可以获取关节角速度和加速度:
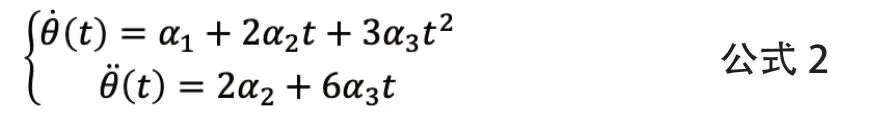
设初始时刻t0=0,并将4个约束条件代入公式1和公式2可得:
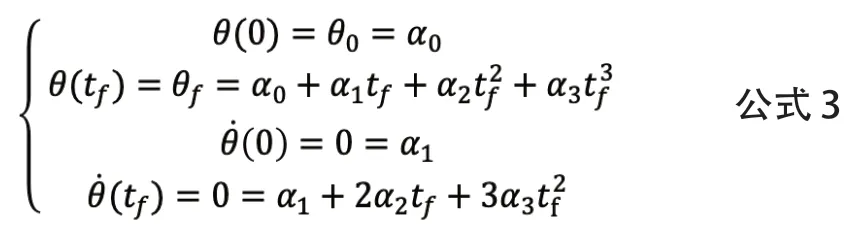
求解以上方程组可得:

将公式4代入公式1得公式5,可求得该关节的轨迹函数。根据公式5可以获取从θ0到θf任意时刻的关节位置。求导后获得该关节的角速度和加速度函数,如公式6所示,速度曲线为抛物线轨迹,加速度曲线为直线轨迹。

1.2 五次多项式插值法
采用三次多项式插值法,机器人关节变量的轨迹曲线和速度曲线能够平滑过渡,但加速度曲线为直线,运动并不平稳。对于运动轨迹的平稳性要求较高的应用场合,可采用五次多项式来规划运动轨迹[3],约束条件增至6个:初始时刻t0和终止时刻tf的关节角度值、角速度值和角加速度值。即:

根据以上6个约束条件可以求得五次多项式表达式,如公式7所示:

对公式7求一阶二阶导数,可得关节角速度和角加速度,如公式8所示:

设t0=0,并将6个约束条件代入公式7、公式8可得公式9:
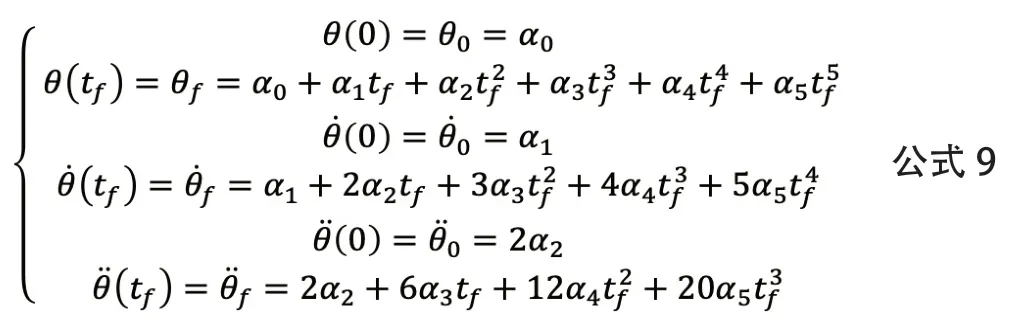
求解以上方程组可得:


将公式11带入公式7可得:

公式12就是该关节的轨迹函数,它确定了从θ_0到θ_f任意时刻的关节位置。该关节的角速度和角加速度如公式13所示,角速度、角加速度曲线均为抛物线轨迹。

2 双臂机器人的运动学模型
Baxter双臂机器人是美国Rethink公司研发一款仿人双臂机器人,如图1所示,由头部、脸部、双臂、可移动底座等部件构成。每条机臂具有7个自由度,而且每个关节都是串联弹性关节,其刚度能够随着工作任务的不同而改变,这种弹性关节让机器人可以更加灵活地完成工作任务,而且能在一定程度上保证人、机交互时更加地安全、可靠。
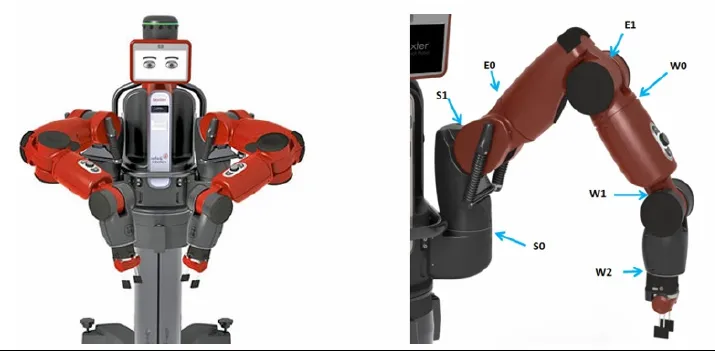
图1 Baxter 双臂机器人

图2 Baxter左臂连杆坐标系
Baxter机器人属于典型的开链串联关节机械臂,前4个关节可以控制机械臂末端位置的状态,后3个关节能够控制机械臂端的姿态。
如图2所示,以Baxter机器人左臂为研究对象,采用D-H法建立机器人的连杆坐标系,相关参数如表1所示。
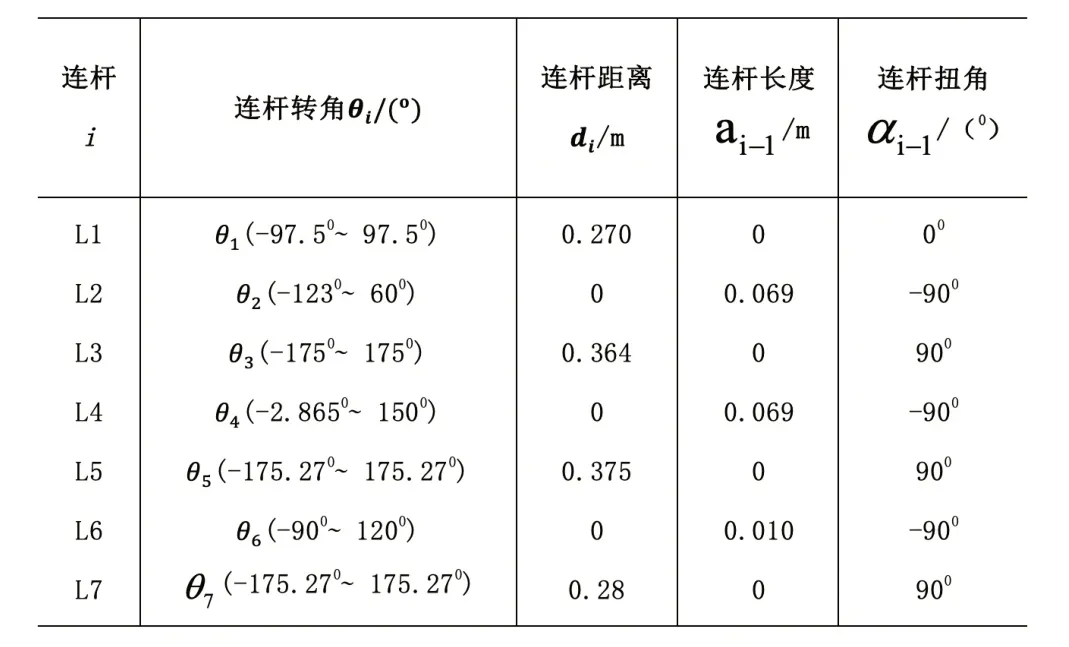
表1 Baxter左臂D-H参数表
运用Robotics Toolbox 编制如下程序,建立双臂机器人运动学模型[4],如图3所示。
L1=Link('d',270,'a',0,'alpha',0);%定义机器人左臂连杆1
L2=Link('d',0,'a',69,'alpha',-pi/2);%定义左臂连杆2
L3=Link('d',364,'a',0,'alpha',pi/2);%定义左臂连杆3
L4=Link('d',0,'a',69,'alpha',-pi/2);%定义左臂连杆4
L5=Link('d',375,'a',0,'alpha',pi/2);%定义左臂连杆5
L6=Link('d',0,'a',10,'alpha',-pi/2);%定义左臂连杆6
L7=Link('d',280,'a',0,'alpha',pi/2);%定义左臂连杆7
robotL=SerialLink([L1 L2 L3 L4 L5 L6 L7]);%建立机器人左臂模型
robotL.display();%显示机器人左臂DH参数
robotL.name='左臂'
thetaL=[0 0 0 0 0 0 0];%设定机器人左臂7个关节的初始关节角
robotL.plot(thetaL);%显示机器人左臂模型
plot(robotL, thetaL);
hold on;
L8=Link('d',270,'a',0,'alpha',0);%定义机器人右臂连杆1
L9=Link('d',0,'a',69,'alpha',-pi/2);%定义机器人右臂连杆2
L10=Link('d',-364,'a',0,'alpha',pi/2);%定义机器人右臂连杆3
L11=Link('d',0,'a',69,'alpha',-pi/2);%定义机器人右臂连杆4
L12=Link('d',-375,'a',0,'alpha',pi/2);%定义机器人右臂连杆5
L13=Link('d',0,'a',10,'alpha',-pi/2);%定义机器人右臂连杆6
L14=Link('d',-280,'a',0,'alpha',pi/2);%定义机器人右臂连杆7
robotR=SerialLink([L8 L9 L10 L11 L12 L13 L14]);%建立机器人右臂模型
robotR.display();%显示机器人右臂DH参数
robotR.name='右臂'
thetaR=[0 0 0 0 0 0 0];%设定机器人右臂7个关节的初始关节角
robotR.plot(thetaR); %显示机器人右臂模型
plot(robotR, thetaR);
hold on;

图3 双臂机器人模型
3 双臂机器人的运动轨迹仿真
利用Robotics Toolbox工具箱中的关节变量空间轨迹规划函数jtraj ,对Baxter机器人的左臂进行仿真研究。设定7个关节角初始值qz=[0 0 0 0 0 0 0],终点关节角值qr=[pi/4 -pi/3 -pi/4 pi/5 pi/3 pi/6 pi/10],执行下列程序代码,可获得各个关节的角度、角速度和角加速度曲线[5],如图4、图5和图6所示。

图4 Baxter机器人的左臂关节空间轨迹曲线
t=[0:0.1:5];%设定仿真时间为5秒
qz=[0 0 0 0 0 0 0];%设定7个关节角的初始值
qr=[pi/4 -pi/3 -pi/4 pi/5 pi/3 pi/6 pi/10];%设定7个关节角的终点值
[q,qd,qdd]=jtraj(qz,qr,t);%利用轨迹规划函数求出各个关节角度、速度和加速度
figure(1)
plot(t,q(:,1),'x');%用“十字”符号绘制关节1的角度曲线
hold on;
plot(t,q(:,2),'p');%用“五角星”符号绘制关节2的角度曲线
hold on;
plot(t,q(:,3),'*');%用“星号”符号绘制关节3的角度曲线
hold on;
plot(t,q(:,4),'-');%用“实线”绘制关节4的角度曲线
hold on;
plot(t,q(:,5),'--');%用“虚线”绘制关节5的角度曲线
hold on;
plot(t,q(:,6),'-.');%用“点划线”绘制关节6的角度曲线
hold on;
plot(t,q(:,7),'^');%用“三角形”绘制关节7的角度曲线
xlabel('时间(s)');ylabel('关节角度(rad)');
title('关节空间轨迹规划');
figure(2)
plot(t,qd(:,1),'x');%用“十字”符号绘制关节1的角速度曲线
hold on;
plot(t,qd(:,2),'p');%用“五角星”符号绘制关节2的角速度曲线
hold on;
plot(t,qd(:,3),'*');%用“星号”符号绘制关节3的角速度曲线
hold on;

图5 Baxter机器人的左臂关节角速度曲线
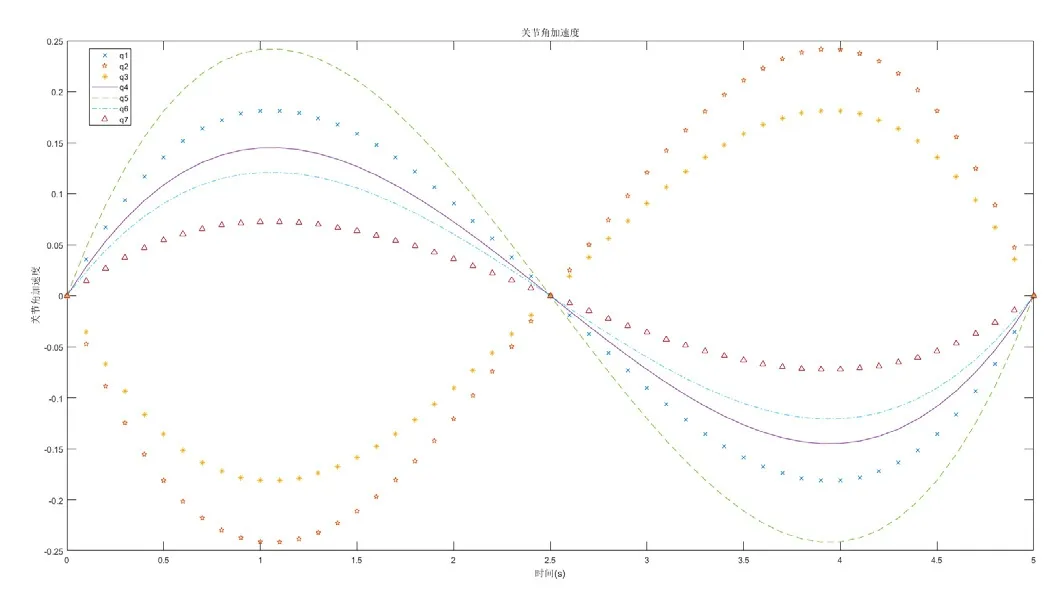
图6 Baxter机器人的左臂关节角加速度曲线
plot(t,qd(:,4),'-');%用“实线”绘制关节4的角速度曲线
hold on;
plot(t,qd(:,5),'--');%用“虚线”绘制关节5的角速度曲线
hold on;
plot(t,qd(:,6),'-.');%用“点划线”绘制关节6的角速度曲线
hold on;
plot(t,qd(:,7),'^');%用“三角形”绘制关节7的角速度曲线
xlabel('时间(s)');ylabel('关节角速度');
title('关节角速度');
figure(3)
plot(t,qdd(:,1),'x');%用“十字”符号绘制关节1的角加速度曲线
hold on;
plot(t,qdd(:,2),'p');%用“五角星”符号绘制关节2的角加速度曲线
hold on;
plot(t,qdd(:,3),'*');%用“星号”符号绘制关节3的角加速度曲线
hold on;
plot(t,qdd(:,4),'-');%用“实线”绘制关节4的角加速度曲线
hold on;
plot(t,qdd(:,5),'--');%用“虚 线”绘 制 关 节5的 角加速度曲线
hold on;
plot(t,qdd(:,6),'-.');%用“点 划 线”绘 制 关 节6的角加速度曲线
hold on;
plot(t,qdd(:,7),'^');%用“三角形”绘制关节7的角加速度曲线
xlabel('时间(s)');ylabel('关节角加速度');
title('关节角加速度');
4 结束语
Robotics Toolbox工具箱中的函数jtraj采用了五次多项式插值方法,利用它仿真双臂机器人的角度轨迹曲线、速度曲线和加速度曲线,这些曲线均为抛物线。三次多项式插值方法的约束条件只有4个:起点和终点的角位移、角速度,而五次多项式插值的约束条件有6个,包括了起点和终点的角加速度,生成的加速度曲线不存在跳变,双臂机器人7个关节角的加速度变化平缓,各关节运动轨迹平稳、连续。
(文责自负)
