高速列车速度跟踪神经网络PID控制器的设计

梁新荣，肖 龙，王雪奇，杨世武，董海荣

1.五邑大学 交通工程系，广东 江门529020

2.北京交通大学 电子信息工程学院，北京100044

近年来，我国经济持续增长，轨道交通建设日新月异，高速铁路研发取得了世界瞩目的成就，高速铁路线路里程和客运量都居全球首位。与此同时，列车驾驶也日益受到人们的关注。人工驾驶受司机个人因素影响大，存在其固有的缺陷，因此学者们非常重视列车自动驾驶（Automatic Train Operation，ATO）的研究，将人工智能和智能控制等先进技术应用到ATO中。列车速度与位置控制是ATO 的研究重点之一，采用的策略是建立合适的列车运行模型，在此基础上，再选择恰当的控制技术使列车按预定的轨迹行驶。

对高速列车进行受力分析并对其进行建模是研究的首要环节，根据牛顿的力学原理可得到列车加速度与其受力之间的动态方程，然而由于列车车厢之间存在非线性耦合关系，在实际建模过程中存在变量多、约束多等问题，列车精确建模具有一定的难度。近年来，研究人员尝试多种建模方法并对列车模型进行简化。从现有的文献来看，列车动态模型主要包括传递函数模型[1-5]、单质点模型[6-14]和多质点模型[15-16]。其中单质点模型把列车看作一个刚体，建模过程相对简单，应用也比较多。多质点模型考虑了车厢之间的耦合和相互作用力，建模过程复杂，目前这方面的研究很少。多质点模型受力作用过于复杂，因此研究的重点在于如何简化多质点模型。另一方面，研究人员探讨了多种ATO算法，其中智能控制算法和先进的优化算法是ATO研究的重点。董海荣等[1]建立了列车二阶传递函数数学模型，并分别用PID控制、模糊控制和模糊PID切换控制对列车二阶传递函数模型进行了仿真研究。马泳娟等[2]对列车进行了受力分析，然后采用模糊预测控制对列车二阶传递函数模型进行了仿真分析。陈小强等[3]研究了高速列车速度控制问题，采用列车二阶传递函数数学模型，并用预测模糊PID 控制对列车传递函数模型进行了仿真实验。米根锁等[4]针对建立的列车传递函数模型，探讨了状态空间描述和极点配置问题，并设计了扰动观测器对列车速度跟踪问题进行了研究。张佩等[5]研究了高速列车具有延时的传递函数模型，采用数据挖掘算法设计控制器对列车数学模型进行控制。上述方法都是基于传递函数模型对列车进行控制仿真，但是一般来说，仅用一个传递函数难以准确描述列车运行过程。蔡鹏翔等[6]建立了高速列车单质点模型，然后用极大似然法和闭环辨识法对列车模型参数进行辨识，最后用PID控制进行了仿真实验。李中奇等[7]研究了高速列车单质点模型，并设计了非线性控制器对列车速度进行跟踪控制。李德仓等[8]研究了高速列车单质点速度微分方程模型，设计了滑模控制器在强风环境下实现了列车速度跟踪控制。郭亮等[9]基于牛顿定律建立了列车单质点微分方程模型，采用扩张状态观测器对期望的速度-距离曲线进行跟踪。杨罡等[10]将高速列车看作为单一质点，根据牛顿定律建立了列车速度微分方程和距离微分方程，采用模型预测控制实现了高速列车的速度跟踪控制。朱雅楠等[11]研究了高速列车单质点微分方程模型，采用广义预测控制实现了列车速度跟踪和位移跟踪。杨辉等[12]建立了高速列车速度微分方程模型，它是一个单质点模型，然后基于Elman网络设计了广义预测控制器对列车速度实施跟踪控制。李中奇等[13]研究了高速列车单质点模型，设计了广义预测控制器对列车期望速度和期望位移进行了跟踪控制。路小娟等[14]研究了高速列车单质点微分方程模型，设计了滑模预测控制器对目标曲线进行跟踪控制。上述文献都是基于单质点模型对列车速度进行控制，单质点模型的缺陷是没有考虑车厢与车厢之间弹性连接器的作用力，也没有考虑各个车厢之间的速度差和加速度差以及车厢之间相对加速度引起的作用力，因而单质点建模准确性不高。Chou等[15]研究了普通低速列车的多质点模型，并对模型进行了校验。董海荣等[16]建立了一种简化的高速列车多质点模型，针对该模型，设计了模糊逻辑控制器对列车速度进行跟踪控制。从以上分析可以看出，绝大多数研究都是采用传递函数模型和单质点模型，对高速列车多质点模型的研究很少，目前还很缺乏。在具体的控制方法上已有研究包括PID控制、模糊控制、神经控制、学习控制、滑模控制、预测控制等。目前的研究重点是智能控制等自适应控制方法，下面阐述的神经网络PID控制属于智能控制范畴。

本文研究了一种多质点模型，称为单位移多质点模型，在此基础上设计了一种实用的BP 神经网络PID 控制器，对高速列车速度进行跟踪控制，并根据数值仿真证明了该方法的有效性。

1 高速列车多质点模型

图1示出一辆高速列车，相邻车厢之间由弹性元件连接起来，其中车厢1为首节车厢，车厢n 为尾节车厢。

图1 一辆高速列车

根据牛顿定律可得到加速度与受力之间的关系式为[16]：

式（1）中，m1,m2,…,mn分别为第1 节，第2 节，…，第n节车厢的质量；ẍ1,ẍ2,…,ẍn分别为下标数字对应车厢的加速度；u1,u2,…,un分别为下标数字对应车厢的牵引力和制动力；fc1,fc2,…,fcn分别为各节车厢的内力，该内力由弹性元件连接器产生；fr1,fr2,…,frn分别为各节车厢的阻力，其中第1节车厢还含有空气阻力。

式（1）为多质点模型，每节车厢都看成一个质点，由于车厢之间存在强耦合关系，式（1）计算工作量相当大，必须对式（1）简化处理。

车厢的内力可表示为：

式（2）中，右边第一个向量的每一项都表示所有前面车厢施加的作用力，右边第二个向量的每一项都表示所有后面车厢施加的作用力。显然，第一个向量的最上面一项和第二个向量的最下面一项都是0。

相邻车厢之间的距离表示为：

式（3）中，xi和xi-1分别为第i 节车厢和第i-1 节车厢的位移，Δxi-1和K 分别表示第i-1 节车厢和第i 节车厢之间距离的弹性可变部分和固定部分。其中弹性可变部分由车钩等弹性元件引起，固定部分与车厢长度有关，易知K 为常数。

对式（3）求导得：

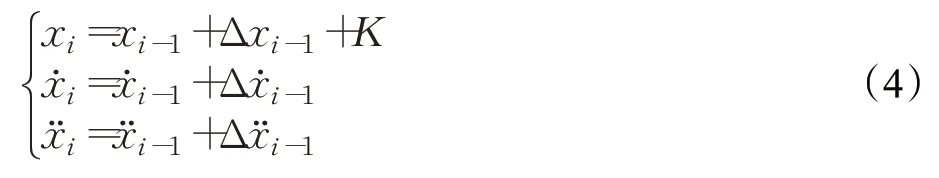
选取第1 节车厢为基准，则由式（4）根据递推关系可得到第i 节车厢的位移、速度和加速度为：

式（5）中，Km为与车厢长度和车厢节数有关的常数。

由式（1）和式（2）得：

由式（5）的第三个等式和式（6）得：

对式（7）两边求和，可得到以首节车厢位移表示的列车动态模型，称为单位移多质点模型，即：

式（8）的模型考虑了车厢间弹性元件连接器的作用，相邻车厢之间存在相对位移，更能反映车厢连接的实际情况，因而该模型比单质点模型更为准确。

关于式（7）两边求和，右边所有的γ(⋅)项抵消问题，还可以换一个角度来解释。

考虑相邻车厢之间的作用力，由式（6）得：

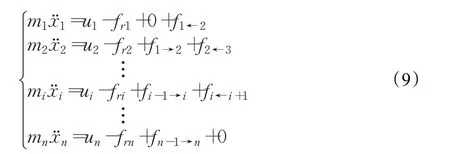
由式（5）的第三个等式和式（9）得：

对式（10）两边求和，并根据作用力与反作用力关系fi-1←i=-fi-1→i，也可得到式（8）的列车多质点模型。

2 列车速度跟踪BP神经网络PID控制

2.1 BP神经网络PID控制

PID控制算法如下[17]：

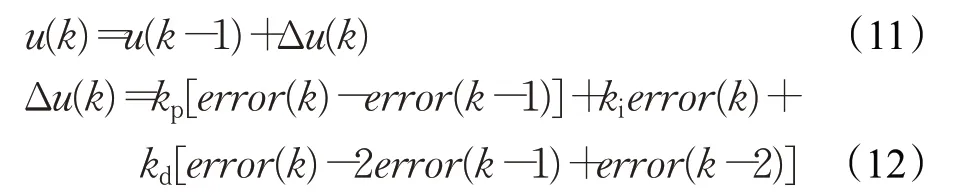
式（11）和式（12）中，u(k)为控制信号，Δu(k)为控制增量；kp、ki和kd分别为比例系数、积分系数和微分系数，error(k)为误差信号。

选取包含输入层、隐含层和输出层的三层BP 神经网络，输入层的输入为：

式（13）中，上角标（1）表示第1 层，即输入层；x(j)表示神经网络的输入；M 为输入层神经元个数。

隐含层的输入和输出为：

输出层的输入和输出为：

图2 示出了BP 神经网络PID 控制对被控对象的控制框图。

图2 BP神经网络PID控制

BP神经网络调整kp、ki和kd的性能指标为：

输出层权值调整公式为：

式（19）中，η 和α 分别表示学习率和惯性常数。等式右边第一项前面的负号表示采用负梯度，即梯度下降调整权值，等式右边第二项为惯性项，惯性项可以加快搜索收敛速度。

性能指标对输出层权值的偏导数为：

根据式（16），式（20）右边最后一项为：

由式（12）和式（16）得：

由式（18）、式（19）、式（20）和式（21）可推导出输出层权值的调整公式为：

式（26）中，g'[⋅]表示函数g(x)的导数。

类似地，可推导出隐含层权值的调整公式为：

式（28）中，f'[⋅]表示函数f(x)的导数。

2.2 列车速度跟踪控制器

对于一辆在具体线路上运行的高速列车，分析行车历史数据，可得到列车期望的速度-时间曲线，与该曲线相对应，还有列车期望的距离-时间曲线。为了实现列车的安全运行，高速列车运行的实际速度曲线和距离曲线应该跟踪期望的曲线，且跟踪误差要尽量小。设计的高速列车速度跟踪神经网络PID控制器如图3所示。

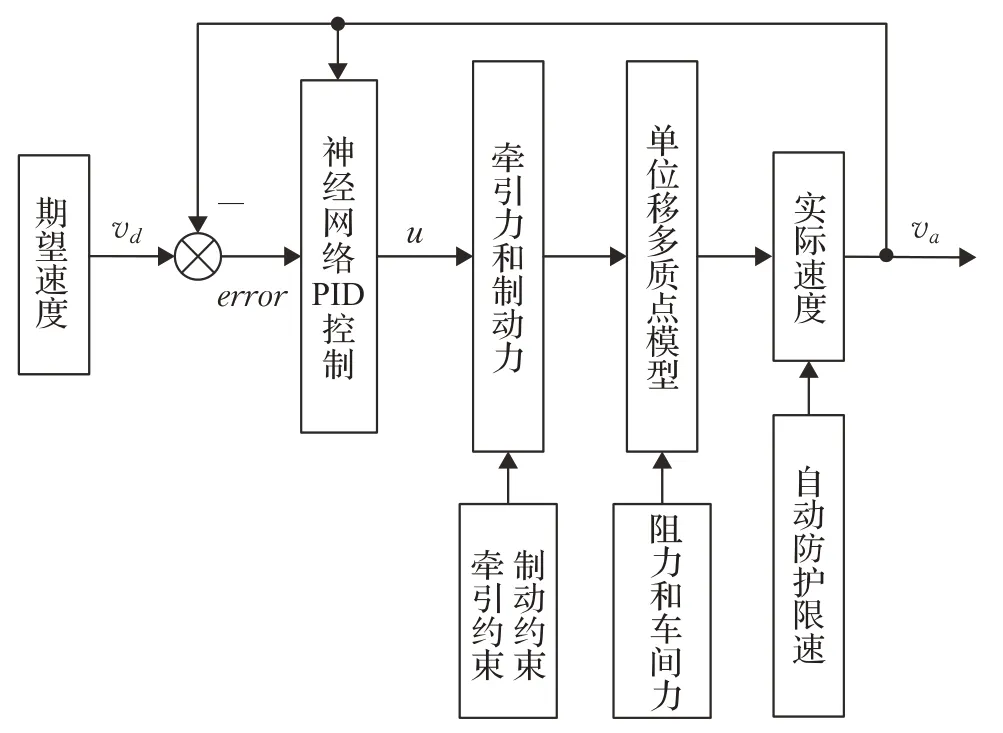
图3 高速列车速度跟踪神经网络PID控制器

图3的期望速度vd与图2的rin相对应，即rin=vd；图3的实际速度va与图2的yout相对应，即yout=va；图3的单位移多质点模型与图2的被控对象相对应，该单位移多质点模型采用式（8）的列车动态模型。根据期望速度vd与实际速度va之间的误差信号，用神经网络PID控制确定单位牵引力和制动力u,u 也是系统的控制量，该控制量决定列车的实际牵引力和制动力。

对于给定的样本数据rin，也即给定列车的期望速度样本数据，下面结合图2 和图3 阐述神经网络PID 控制算法。

（1）确定BP神经网络输入层、隐含层和输出层的节点数，并给出神经网络的初始权值。在本文后面的仿真中，神经网络的输入层节点数M 为4，隐含层节点数Q为5，输出层节点数为3，该输出层节点输出PID参数kp、ki和kd。

（2）根据系统输入和输出，计算误差信号，计算公式为error(k)=rin(k)-yout(k)=vd(k)-va(k)。

（3）根据2.1 节相关公式计算神经网络各层的输入和输出。

（4）根据式（11）和式（12）计算控制量u(k)。

3 仿真结果

对图3所示的高速列车速度跟踪神经网络PID控制器进行数值仿真，仿真对象为一辆8 节车厢的高速列车，采用本文的高速列车多质点模型。式（8）中车厢的阻力包括了滚动阻力、空气阻力、坡道阻力和弯道阻力，在仿真时把滚动阻力和空气阻力合并为基本阻力(a+bv+cv2)，并把坡道阻力和弯道阻力计入附加阻力中。式（8）的多质点模型还存在车厢之间的相互作用力，该作用力与车厢之间的相对加速度有关。期望速度样本数据和列车参数数据来源于北京交通大学，共有500个期望速度样本点，列车重量为840 t（t为吨），基本阻力公式中a=0.53,b=0.003 9,c=0.000 114 ；ATP 限速为405 km/h，利用ΜATLAB 软件根据2.1 节和2.2 节的算法编写仿真程序。在一台普通的Intel Core i3、内存为4 GB的计算机上运行程序，神经网络对500个样本数据的训练时间仅为0.1 s，这么短的训练时间说明该神经网络PID控制器完全可以在线工作。

图4、图5 和图6 分别示出了速度跟踪曲线、距离跟踪曲线和速度跟踪误差曲线。可以看出，实际速度曲线与期望速度曲线几乎完全重合（个别点除外），实际距离曲线与期望距离曲线完全重合，说明本文设计的神经网络PID 控制具有优越的跟踪性能。从图6 还可以看出，在跟踪过程中，多数跟踪点的速度跟踪误差都在0附近上下波动，少数跟踪点存在较小的速度跟踪误差，最大点的速度跟踪误差维持在±4 km/h的范围内。

为了比较，在期望速度样本数据和列车参数数据完全相同的情况下，还采用模糊控制和常规PID控制进行了仿真实验。实验表明模糊控制和常规PID 控制也能实现速度跟踪和距离跟踪，但跟踪性能不同。表1示出了三种方法的性能比较。从表1可以看出，神经网络PID控制的速度跟踪误差范围、速度跟踪平均误差和距离跟踪平均误差在三种方法中都是最小的。

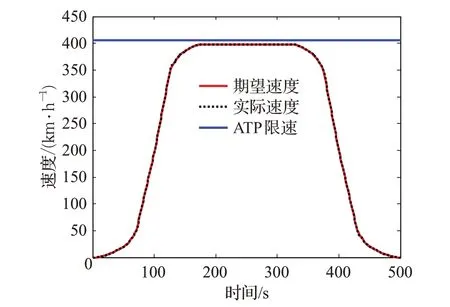
图4 速度跟踪

图5 距离跟踪

图6 速度跟踪误差

表1 三种方法性能比较

为了进一步说明基于多质点模型的神经网络PID控制的建模及控制效果，本文还对存在外界扰动和参数变化这两种情况分别进行仿真验证。

图7 是系统有随机噪声扰动时的速度跟踪曲线，图8 是系统有随机噪声扰动时的速度跟踪误差曲线。从图7 和图8 可以看出，尽管系统存在较大的随机噪声扰动，速度跟踪性能还是比较好的。速度跟踪误差范围仍在±4 km/h 内，与图6 的速度跟踪误差范围相同。而且图8中大多数时间点的速度跟踪误差都在0附近上下波动，波动幅度维持在0.35 km/h范围内，速度跟踪平均误差为0.348 6 km/h。

图7 有噪声时的速度跟踪

图8 有噪声时的速度跟踪误差

高速列车遇到阵风等不确定性因素时，模型参数会出现变化。图9是在基本阻力参数发生突变（增大2倍）时的速度跟踪曲线，图10 是参数突变时的速度跟踪误差曲线。图9的速度跟踪曲线与正常情况下图4的速度跟踪曲线没有明显的差异，图10 的速度跟踪误差曲线与正常情况下图6的速度跟踪误差曲线也很接近。图10的速度跟踪误差范围依然维持在±4 km/h 内，速度跟踪平均误差为0.204 4 km/h，说明本文方法能很好地克服参数变化对控制性能的影响。当系统存在某种不确定性因素导致模型参数变化时，实际速度仍然能够高精度地跟踪期望速度。

图9 参数突变时的速度跟踪

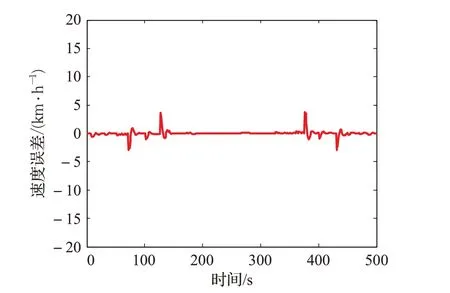
图10 参数突变时的速度跟踪误差

为了更进一步验证神经网络PID 控制器的跟踪性能，下面再增加一个不同环境下的仿真。该仿真的期望速度曲线来源于文献[8]，列车运行方式经历了启动—恒速350 km/h—减速—恒速180 km/h—提速—恒速320 km/h—制动等阶段。ATP 限速为360 km/h，仿真对象仍为一辆8 节车厢的高速列车，采用多质点模型，列车受到的阻力公式和列车重量与第一个仿真相同，所使用的计算机配置也保持不变。

图11、图12 和图13 分别给出了第二种期望速度下的速度跟踪、距离跟踪和速度跟踪误差。从图11 和图12可以看出，神经网络PID 控制具有很好的跟踪性能，速度跟踪平均误差为0.047 8 km/h，距离跟踪平均误差为0.874 7 m。从图13还可以看出，除少数几个点外，绝大多数点的速度跟踪误差都在0附近轻微变化，最大点的速度跟踪误差维持在±1.8 km/h的范围内。

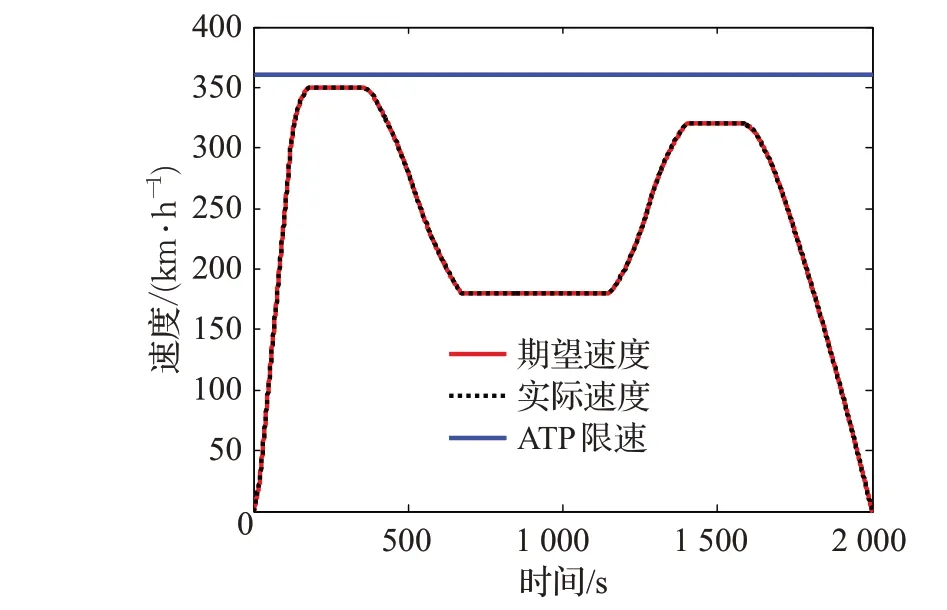
图11 第二种期望速度下的速度跟踪

图12 第二种期望速度下的距离跟踪

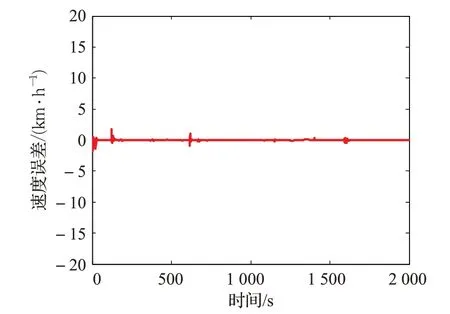
图13 第二种期望速度下的速度跟踪误差

在第一个仿真中已经比较了神经网络PID控制、模糊控制和常规PID 控制的跟踪性能（见表1），这里再对这三种方法的时间性能进行比较。在一台普通的Intel Core i3、内存为4 GB的计算机上，神经网络PID控制对2 000个样本数据的训练时间为0.16 s。同样是2 000个样本数据，模糊控制的训练时间为32.25 s，常规PID 控制的训练时间为0.09 s。从时间性能上来看，神经网络PID 控制也是很有优势的，略大于常规PID 控制的训练时间，但远小于模糊控制的训练时间。

4 结论

针对高速列车运行过程的复杂非线性关系以及多质点模型耦合变量多等特点，建立了一种简化的只考虑首节车厢位移的多质点模型，即单位移多质点模型，设计了一种实用的神经网络PID控制器，对高速列车期望速度进行跟踪控制，并与模糊控制以及PID控制进行了仿真对比。仿真实验表明，本文提出的神经网络PID控制极大地提高了跟踪控制精度，满足了列车正点运行的需求。