QPSO算法的改进及其在DBN参数优化中应用
2021-05-26于国龙崔忠伟
于国龙,赵 勇,吴 恋,崔忠伟
1.贵州师范学院 数学与大数据学院,贵阳550018
2.北京大学深圳研究生院 信息工程学院,广东 深圳518000
量子粒子群算法(Quantum Particle Swarm Optimization,QPSO)是智能计算中性能最好的寻优算法之一。它是一种改进的PSO 算法,首先由孙俊等人提出。QPSO算法不同于传统的PSO算法,它定义粒子运动在量子空间中,粒子的运动没有轨迹,而是依概率出现在解空间中的任意一个位置,粒子可以依概率覆盖整个解空间,从而QPSO算法可以依概率1收敛于最优解,这是传统PSO算法做不到的,因此QPSO算法有着较强的全局搜索能力[1-3]。QPSO 算法被广泛地用于解决资源调度、路径寻优、方案优化等问题,受到产业界和研究人员的广泛关注,但QPSO 算法也存在许多不足之处,如在有限次迭代下也会陷入局部最优,收敛速度有待提高,收敛精度不高等问题。针对存在的问题研究人员对QPSO 算法的优化做了大量的工作。Wang 等人提出了一种基于动态惯性的分类进化QPSO算法,使算法具有较强的适应性,提升了QPSO算法的搜索效率[4]。Xue等人提出了一种基于自然选择的QPSO算法,该算法将粒子进化过程中的单个粒子进化率和群体分散性与自然选择方法相结合[5]。Taherzadeh等人提出了一种SP-UCI与QPSO 算法结合的QPSO 算法(SP-QPSO),SP-QPSO使用基于复合构建和维数监测的SP-UCI策略,然后基于QPSO算法逐步演化[6]。这些工作大多从粒子群的结构和算法融合出发来进行优化,考虑到在QPSO 算法中,粒子势阱长度对算法的收敛性能影响最大,于是本文提出了一种基于粒子势阱长度变化率比重,决策粒子平均最优位置计算中各个粒子所占权重的方法来调节势阱长度,从而调节粒子的寻优能力。
本文将改进后的QPSO 算法应用于DBN 网络参数优化中,来寻优最优DBN网络参数,并建立了一个基于蛋黄形状检测的LQ_DBN 模型,用于以大量蛋类为原料的食品生产企业中,来进行无损伤地检测所采购的蛋类是否变质。企业的传统做法是采用人工经验辨别、暗室强光观察蛋内部、称重法等,这些方法人工成本高,工人工作量大,识别准确率低。随着技术的发展,国内外研究人员采用了近红外、声学、机器视觉等技术来实现鲜蛋无损检测[7-8]。这些方法较之传统人工方法有了较高的检测效率和准确率,但这些方法需要的硬件设备成本高,系统建设复杂,模型建立难度高。随着人工智能技术的兴起,DBN网络有着较高的图像识别率,且模型训练简单,不需要复杂的硬件设备支持。在实际生产中,变质蛋的蛋黄会与蛋清融合,强光下观察蛋黄与蛋清边界模糊且不平滑,不规则;而没有变质的蛋黄与蛋清边界清晰,边界边缘平滑且规则,由此特征可以判别鲜蛋是否变质[9-11]。因此本文基于蛋黄的形状来构建检测蛋类是否变质的DBN 网络模型,并通过QPSO 算法对DBN网络参数选择进行了优化。最后通过实验测试表明,本文方法建立的LQ_DBN 模型较之典型的CCPSO-DBN、PSO_ΜDBN和标准DBN模型有着更高的检测识别准确率,而且本文模型的检测准确率也较其他三种模型更稳定。
1 QPSO算法分析及改进
1.1 QPSO算法收敛性能分析
QPSO算法是一种具有量子行为的PSO算法,不同于PSO算法的是,PSO算法粒子处于牛顿空间中做轨迹运动,而QPSO 算法中的粒子是处于量子空间中,粒子依概率出现在空间中的任何点,而且QPSO算法可以以概率1在解空间收敛。若粒子寻优空间中有N 个代表寻优解的粒子,第i 个粒子在D 维搜索空间的位置为Xi=(xi1,xi2,…,xiD),粒子i 每次迭代局部最优位置为pbi=(pbi1,pbi2,…,pbiD),整个粒子群的全局最优位置为gbi=(gbi1,gbi2,…,gbiD)。在量子空间中用波函数ψ(x)来确定粒子的状态,粒子在空间中某一位置r 出现的概率Q(r)可以用 ||ψ(r)2表示,以三维空间为例,Q(r)满足归一化条件,则存在式(1)[12-14]:
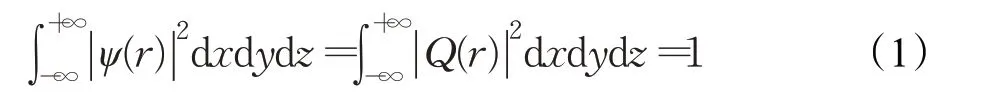
在量子系统中,粒子在δ 势阱中的定态薛定谔方程如式(2):

其中,E 为粒子的能量,h为普朗克常量,m 为粒子的质量。则解式(2)可得到波函数,如式(3)所示:

假设粒子i 第t 次迭代时,在d 维的势阱为pbid(t),则粒子i 第t+1 次迭代的波函数ψ(x)为[15]:

采用蒙特卡罗方法对粒子位置进行随机采样,可得到粒子在第t+1 次迭代时,第i 个粒子第d 维的位置分量xid(t+1)。势阱特征长度Lid(t)的值由式(5)计算:
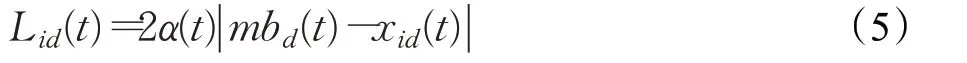
其中,α 为收缩-扩张系数,mb 称为平均最优位置,它是所有粒子自身最优位置的中心点,是粒子在所有维度上的个体最优值的平均值,mb 的计算如式(6)所示:

QPSO 算法与经典PSO 算法的最大区别在于粒子位置更新方法的不同。它在更新粒子位置时,除了综合考虑了当前粒子的局部最优位置和全局最优位置,还引入了粒子平均最优位置mb,增加了粒子之间的相互作用,加强了粒子群的全局搜索能力。
由平均最优位置mb 计算公式(6)可以看出它是每个粒子位置局部最优值的平均值,它决定了粒子位置的更新。在mb 的计算过程中,每个粒子局部最优值pbi(t)所占的权重相同,每个粒子的位置在mb 的计算中所占的比重都是1,即每个粒子对最终的平均最优位置mb决策影响力是相同的,这不符合群体智能决策策略。为了考虑到每个粒子的收敛特性,对粒子势阱长度对收敛的影响进行分析。QPSO 算法中粒子的势阱长度决定了粒子的搜索范围,它决定了粒子收敛性能。
如式(3)中ψ(r)描述了粒子迭代时以多大概率出现在位置r ,若以r=0 为势阱中心,通过分析可以知,当r →0 时有:
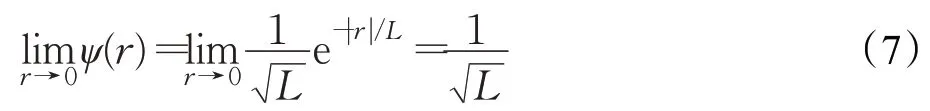
由式(7)可以得知,当r →0 时,粒子迭代位置出现在势阱中心的位置与粒子势阱长度成反比关系,即粒子势阱长度越小,粒子出现在势阱中心的概率就越大,反之越小。同时,粒子越靠近势阱中心,迭代越稳定,势阱长度变化就越小。可以利用粒子平均最优位置mb 来调节粒子的势阱长度L。基于以上分析本文考虑由粒子势阱长度变化率来确定粒子平均最优位置计算中,每个粒子局部最优值的权重。使得势阱长度变化较小的粒子,即搜索能力较弱的粒子,在迭代中获得较大的势阱长度,提升粒子的搜索能力,防止QPSO 算法因粒子早熟而陷入局部最优。
1.2 平均最优位置权重计算方法改进
针对上文的分析,为防止粒子早熟而使算法陷入局部最优。本文引入一个平均最优位置计算权重系数η,ηi(t)表示粒子在第t 次迭代中,第i 个粒子的局部最优值pbi(t),在粒子平均最优位置mb(t)计算中所占的权重。考虑势阱长度对粒子收敛于势阱中心概率的影响,权重值用粒子迭代中最近两代的势阱长度变化率的比重来表示,针对种群规模为N 的粒子群,ηi(t)的具体计算公式如式(8)所示:

ΔLi(t)为第t 次迭代时,粒子势阱长度在第t-1 和t-2 两代的变化率,具体如式(9)所示。它用来衡量粒子相邻两代的粒子势阱长度变化情况,为了满足计算条件,变化率从粒子第三代开始计算,即t=3 时开始计算。

ΔLsum(t)为第t 次迭代时,所有粒子在第t-1 和t-2 两代的势阱长度变化率之和。其中,变化率之和也是从粒子第三代开始计算,即t=3 时开始计算,且有ηi(1)=1/N ,ηi(2)=1/N 。

由式(8)~(10)可知权重ηi(t)的大小取决于粒子势阱变化率ΔLi(t),ΔLi(t)越小,权重ηi(t)也越小,反之,ΔLi(t)越大,权重ηi(t)也越大。ΔLi(t)越小说明粒子上两代迭代中势阱长度变化较小,粒子趋于收敛于势阱中心,这时以较小的ηi(t)作为粒子平均最优位置计算的权重,可使粒子平均最优位置远离势阱中心,增加粒子的势阱长度,提升粒子的全局搜索能力,避免粒子陷入早熟。
引入权重系数η 后,粒子个体平均最优位置mb(t)的计算公式(6),可表示成式(11),N 为粒子规模。

1.3 改进后QPSO算法性能分析
为了验证优化后的QPSO算法的收敛性能,本文将优化后的QPSO算法与标准QPSO算法和文献[16]中的IEQPSO 算法进行了对比,对比过程中采用与文献[16]中表1 提供的8 个标准测试函数f1~f8作为本文的测试函数集,来检测三种算法在测试函数上的全局和局部寻优能力,这8个测试函数均具有最小值。实验中所采用的算法参数与文献[16]中的参数完全相同,同样进行50次实验,测得平均最优值和标准差如表1所示。
通过表1的测试结果可以发现,本文算法在标准测试函数f1~f8上的寻优结果均优于标准QPSO算法和文献[16]的IEQPSO算法,特别在f4和f5最优值比较复杂且易于陷入局部最优的测试函数上,本文算法仍然比其他两种算法有着较好的寻优能力。说明本文改进后的QPSO算法的全局寻优能力上要优于另外两种算法,其能快速地搜索到最接近测试函数最小值的最优解,寻优过程中能更好地避免QPSO 算法陷入局部最优。通过实验结果分析可知,本文通过引入平均最优位置计算权重系数η,使得改进后的QPSO算法有着更强的全局搜索能力。

表1 测试函数运行的均值与标准方差
在改进后的QPSO算法中,由式(8)和式(10)可知,粒子i 的平均最优位置计算权重系数ηi(t)的计算过程中,由粒子种群中所有粒子的势阱长度参与计算,这增加了粒子间的信息交互,增强了种群的多样性。现就不同阶段整个粒子群及最优粒子的寻优能力,通过f1~f8测试函数进行寻优对比分析,如图1所示。
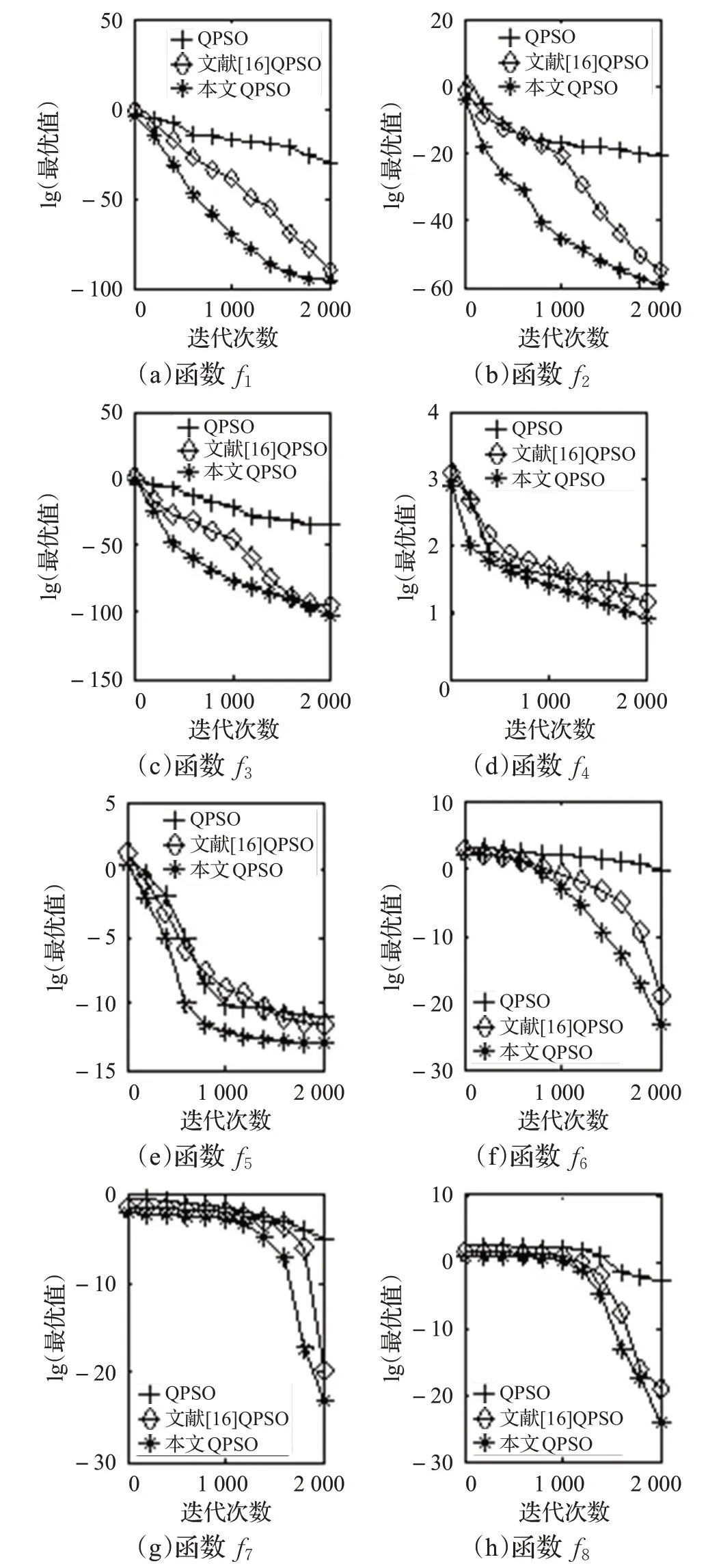
图1 测试函数寻优结果对比
从图1 的仿真对比结果可以看出,本文改进后的QPSO算法在8个标准测试函数上的寻优效果要优于原始QPSO算法和文献[16]的优化QPSO算法。随着迭代次数的增加,整个粒子群寻优的精度和速度都有明显改善,特别在f1、f2、f5和f6函数上的寻优结果要远远好于另外两种算法。粒子在迭代的初期对解空间的探索能力较强,在吸引子的作用下会迅速向最优解靠拢,这时粒子的势阱长度总体的变化率会较大,在后期粒子总体都聚集在最优解附近,相应的势阱长度变化也就较小,这是粒子群迭代过程中势阱长度变化的趋势。在粒子群寻优过程中,最优粒子就是离最优解最近的粒子,但这个最优解也有可能是局部最优解,而不是全局最优解,这时在平均最优位置的计算中,可以让该粒子的位置计算权重相对较小,使平均最优位置远离这个最优解,增大粒子的势阱长度,以增强粒子的搜索能力,从而避免粒子陷入局部最优解,增强粒子的全局寻优能力。
针对本文优化后的QPSO 算法的复杂度进行如下分析。现假设粒子群的规模为N ,维数为D,为了方便对比优化后的QPSO 算法与标准QPSO 算法的复杂度,这里设迭代次数为T 。在QPSO算法迭代过程中,相关的计算如粒子适应度的计算、粒子历史和全局最优位置的更新、粒子位置更新等操作均为常数级复杂度,其中粒子平均最优位置的计算复杂度为O(mb)=O(D×N),那么标准的QPSO算法的复杂度就为O(D×N×T)。相对于标准QPSO算法的计算复杂度,本文算法主要增加了粒子的平均最优位置计算权重系数η 的计算量,由式(8)~(10)可知O(η)=D×N ,因此优化后的QPSO 算法的复杂度仍为O(D×N×T)。
2 DBN网络模型优化
2.1 DBN网络模型和训练方法
假设有一个二部图,每一层的节点之间没有链接,一层是可视层,即输入数据层(v),一层是隐藏层(h),如果假设所有的节点都是随机二值变量节点(只能取0或者1 值),同时假设全概率分布p(v,h)满足Boltzmann分布,称这个模型是受限玻尔兹曼机(Restricted Boltzmann Μachine,RBΜ),模型如图2所示[15-16]。

图2 受限玻尔兹曼机模型
RBΜ 可以通过对比散度(Contrastive Divergence,CD)算法,用重构数据代替原始模型来实现无监督训练,提高训练的效率。深度置信网络一般由多层受限玻尔兹曼机组成,常用的DBN网络模型如图3所示。

图3 DBN网络模型
从图3 可以看出,每相邻两层构成一个RBΜ,每一层的隐藏层同时也是它的下一层的可视层,最底层可视层接受样本数据输入。网络的同层节点之间是没有连接的,如果一个DBN网络具有m 层隐含层,那么可视层v 和隐藏层h 的关系可用联合概率分布表示如下[17-19]:

DBN 网络在训练过程中,网络所要学习的就是联合概率分布P(v,h1,h2,…,hm),而P(v,h1,h2,…,hm)就是对象的生成模型。
RΜB 又可视为基于能量的模型,其能量函数定义如公式(13)所示:

其中,wij表示可见单元vi与隐单元之间的连接权重,ai表示可见单元vi的偏置,bj表示隐单元hj的偏置,wij,ai,bj∈R。
DBN网络的训练一般通过分层训练和调参数两步完成,每次训练一层RBΜ,然后训练结果作为下一层的输入,待训练完成后,展开网络对整个网络进行优化调整,网络结构参数多以经验值来设定,这些经验值往往是通过多次实验测得,这些实验值往往不能达到网络最优化,导致网络精度不高,且训练效率也较低,QPSO算法具有较强的寻优能力,利用QPSO算法可以解决上述问题。
2.2 基于改进后QPSO算法的DBN参数优化
对于上述深度信念网络(DBN)模型,最主要的任务是求出参数的值,来拟合给定的训练数据。Hinton提出了对比散度(Contrastive Divergence,CD)算法。通过CD算法,可以获取一次梯度上升迭代中,显层和隐层之间的连接权重矩阵w 、可视层的偏置向量a 、隐藏层的偏置向量b 的偏导数Δwij、Δai、Δbj。则参数更新如式(14)~(16)所示:

其中,ηw、ηa、ηb为学习率,t 为迭代次数。QPSO算法以网络的输出值与标签期望值的误差作为适应度函数,误差越小那么粒子的寻优能力就越强,当误差值达到要求时,即粒子收敛于最优解,表示找到网络的最优参数。
DBN网络参数的选择优劣最终决定了所生成模型的识别精度和效率,如学习率和迭代次数的选择。因此本文采用量子粒子群优化算法QPSO 对DBN 网络参数进行优化。QPSO 算法中粒子的运动状态用波函数来表示,取代粒子牛顿空间运动,用波函数的概率密度函数来确定某一次迭代,粒子在解空间中的位置,这个位置是随机的,只要粒子不停地迭代,就会以某一概率经过解空间任意一个位置。粒子根据量子行为不断地更新自己的位置,逐渐向全局最优解迭代。粒子搜索过程中的量子行为使得QPSO算法的全局收敛能力大幅提升。
QPSO 算法粒子的适应度值计算,考虑从模型的检测误差大小来定义适应度函数F ,具体表示如式(17)所示:

其中,si为样本i 的重构值;li为样本i 的标签值。误差值越小DBN网络模型检测效果越好,准确率越高,模型的参数求解越趋于最优。整个QPSO算法优化DBN模型参数的算法框架如图4所示。将通过本文改进后QPSO算法优化的DBN模型称之为LQ_DBN模型。
当需要构建另一个DBN网络来解决不同的检测任务时,因为检测的对象变化了,这时需要重新训练DBN网络模型,但只需要给定新的任务训练样本,设定好期望的检测误差值,作为QPSO算法迭代的结束条件,就可以通过QPSO算法对新构建DBN网络参数进行寻优。
DBN网络模型的收敛性主要涉及到模型的训练时间和训练精度。首先针对于训练时间,传统的DBN 网络模型训练需要靠人工以经验值来进行ηw、ηa、ηb学习率参数的调整,通过训练得到要构建的模型显层和隐层之间的连接权重矩阵w、可视层的偏置向量a、隐藏层的偏置向量b,再由式(13)构建RΜB模型,从而得到符合要求的DBN 网络。人工参数确定的过程中,由于涉及的参数较多,组合可能性庞大,将会大大增加模型的训练时间。而采用QPSO 算法来代替人工训练DBN 模型,可视为QPSO 算法在三维空间中寻优,整个寻优过程只需要在式(17)的监督下自动完成,不需要人为干预,可以高效快速地完成DBN网络的训练,大大缩短网络训练的时间。然后在模型的训练精度上,无论是哪种训练方法,都需要式(17)所计算的检测误差大小来确定最终的DBN 网络参数,即基于这样一个检测精度来反向寻找网络参数。最终DBN网络模型的收敛性取决于QPSO算法的收敛性和对网络的预期检测误差要求。

图4 QPSO算法优化DBN模型参数算法框架
3 基于LQ_DBN的蛋黄形状检测应用
3.1 蛋黄形状检测流程
在研究过程中,变质蛋较难收集,因此负样本量相对正样本数量要少,为了提高检测的效率和准确性,在输入DBN网络前对图像经行了预处理,如图5所示。图像的预处理分为图像灰度化、图像二值化、图像锐化等过程实现。
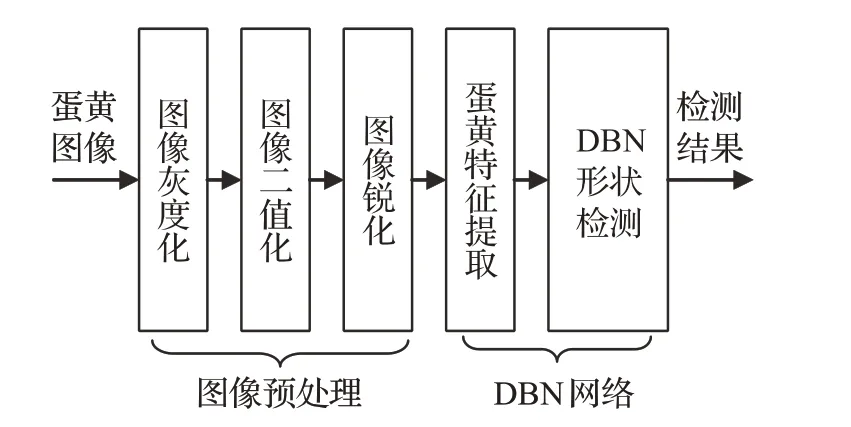
图5 蛋黄形状检测流程
预处理完的图像经过DBN网络来提取蛋黄形状的特征,并根据训练模型进行分类检测,最终通过DBN网络得到相应的检测结果。
3.2 DBN分类器的结构设计
考虑均衡DBN 网络的训练时间和模型精度,经实验验证本文设计了含有三个隐含层的DBN 网络,具体的网络结构如图6所示[17]。

图6 DBN分类器结构
图6中,h1~h3分别为网络中的三个隐含层,x 为输入层,y 为输出层,在x 层输入待检图像特征向量,经由三个隐含层,得到分类结果y。k1~k3分别为隐含层包含的单元个数。由于输入端输入的是二值向量,所以这里选用二值单元,其激活函数采用sigmoid激活函数,如式(18)所示[18-19]:

4 实验及结果分析
4.1 实验条件及参数
实验中将本文建立的LQ_DBN 网络模型与文献文献[20]中的PSO_ΜDBN、文献[21]中的CC-PSO-DBN网络模型及标准DBN 网络模型,进行蛋黄检测对比。QPSO算法优化DBN网络参数的设定时,选择初始粒子种群规模为30,维数为3,QPSO 算法收缩-扩张系数为α,它的取值会直接影响算法的收敛性能,本文α(t)的取值如式(19)所示[22-24]。其他的DBN 网络模型建立中涉及到的参数,均采用原文的参数。

4.2 蛋黄采样图像预处理
实验利用图7中项目组开发的鸡蛋质量检测系统,来对蛋黄进行样本采集和检测,其中图7(a)是蛋黄图片样本采集装置示意图,图7(b)是蛋黄检测相关软件系统。实验前期采集了10 000 张正常蛋在强光下的蛋黄图片作为正样本图片,2 000 张变质蛋在强光下的蛋黄图片作为负样本图片,如图8(a)和(b)所示。将采集的蛋黄样本按照上文中的预处理过程处理后得到的预处理图片如图9(a)和(b)所示。
4.3 蛋黄形状检测结果分析
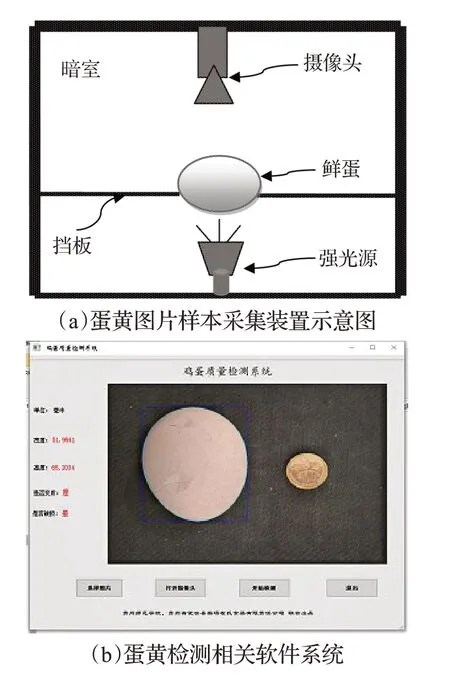
图7 鸡蛋质量检测系统
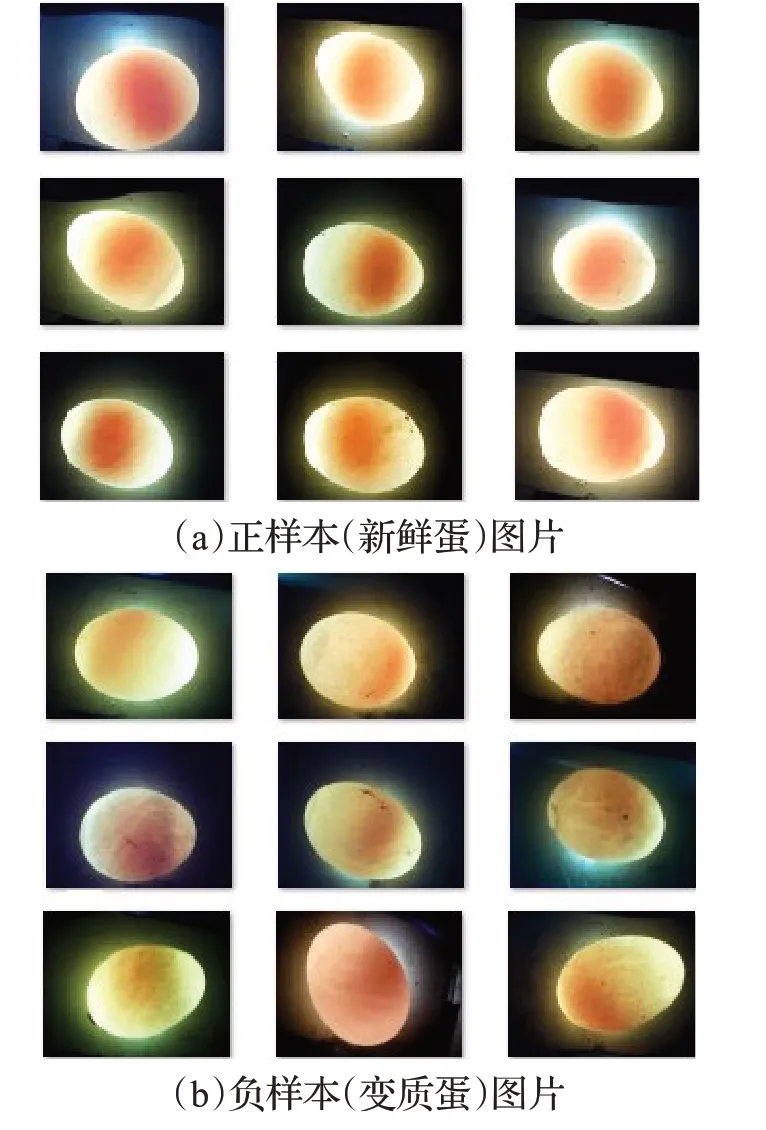
图8 采集的蛋黄正负样本图片
利用上文中构建的LQ_DBN网络模型,通过图7的检测系统,来对实时采集的蛋黄样本进行检测实验,并与CC-PSO-DBN、PSO_ΜDBN和标准DBN模型检测方法进行了对比。因为训练模型时正负样本存在差异,为了更好地说明实验效果,所以本文对四种算法在正常蛋、变质蛋和随机选蛋三种情况下分别做了检测实验,来验证模型的检测准确率,并对检测准确率进行了统计分析。具体实验中选择了正常蛋做了200次检测测试,变质蛋做了200次检测测试和随机选择蛋做了500次检测测试,最终的识别准确率结果分别如图10~图12所示。

图9 蛋黄样本预处理图片

图10 正常蛋检测准确率
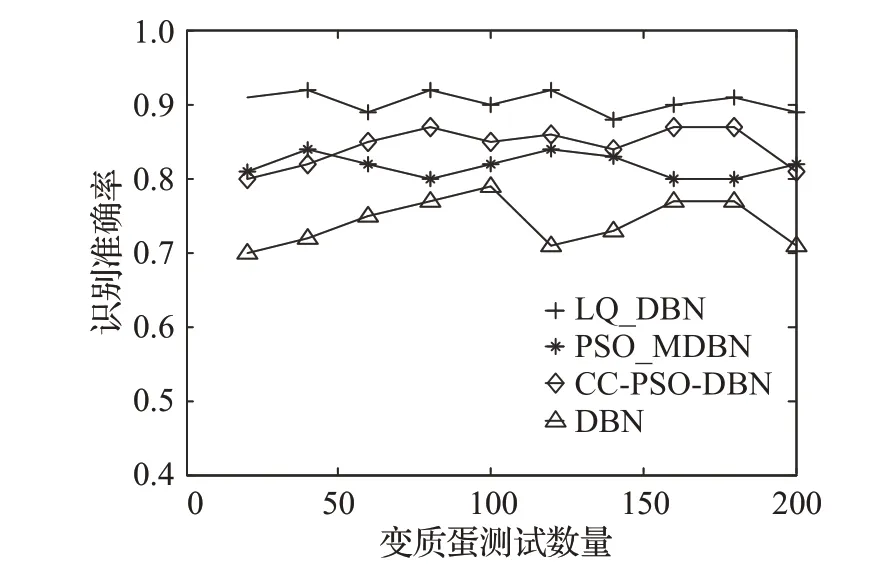
图11 变质蛋检测准确率
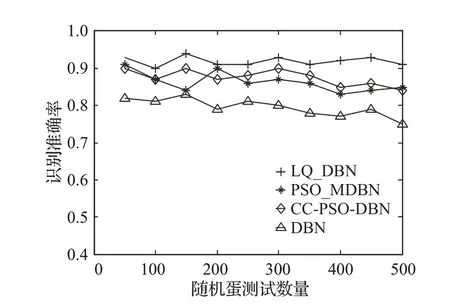
图12 随机蛋检测准确率
从图10 正常蛋的检测准确率结果对比可以得出,四种模型的检测识别准确率都超过了80%,尤其本文LQ_DBN 网络模型的识别准确率最高,达到了90%以上,标准DBN 的识别准确率在四种模型中最低。PSO_ΜDBN和CC-PSO-DBN模型的识别准确率相差不大,但均好于标准DBN 的识别准确率。图11 曲线则反映了四种模型对变质蛋检测的准确率,通过对比可以看出,本文LQ_DBN 网络模型的识别准确率仍然最高,PSO_ΜDBN和CC-PSO-DBN模型次之,但CC-PSO-DBN模型要比PSO_ΜDBN 模型更好,这三个模型检测识别准确率都在80%以上,而标准DBN 的识别准确率相对其他三种模型最低,仅仅在70%~79%之间。最后通过随机选取正常蛋和变质蛋再进行检测对比,如图12,本文LQ_DBN 网络模型的识别准确率依然最高,达到了90%以上,而PSO_ΜDBN 和CC-PSO-DBN 模型则相差不大,CC-PSO-DBN模型略好于PSO_ΜDBN模型,标准DBN模型的识别准确率仍然是四个对比模型里面最低的。从以上实验中还可以发现,四种模型的正常蛋样本的检测率普遍要高于变质蛋样本的检测率,这是因为变质蛋样本在DBN 模型训练时样本量要少于正常蛋样本,且变质蛋的样本采集受光线环境和蛋壳厚度等条件制约,导致了部分负样本被错误地识别成了正样本。通过以上三组实验对照分析,LQ_DBN、CC-PSO-DBN、PSO_ΜDBN 和原始DBN 四个模型对蛋黄形状的检测识别率中LQ_DBN最高,说明本文通过改进的QPSO算法对DBN模型的优化达到了预期效果。
为进一步比较四种检测模型的检测稳定性,分别计算了它们的识别准确率标准差,如表2~表4所示。检测模型的稳定性跟模型的本身参数、样本的质量,样本数量等都有一定的关系。这里只对本次实验结果做一个统计比较。

表2 正常蛋测试准确率方差统计表
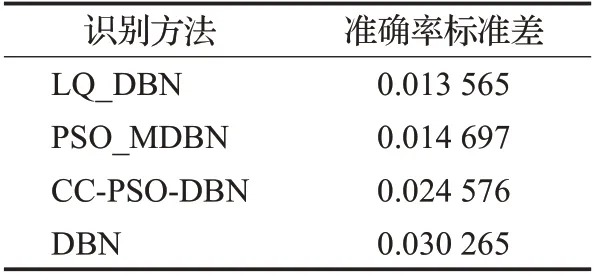
表3 变质蛋测试准确率方差统计表

表4 随机蛋测试准确率方差统计表
从三个统计表可以发现,在正常蛋、变质蛋和随机蛋检测中,本文的LQ_DBN 模型的识别准确率变化较其他三种模型要稳定,其中,在正常蛋检测中,本文LQ_DBN 模型与PSO_ΜDBN 模型的稳定性较为接近。三组测试中,标准DBN 模型的稳定性相对其他三种模型是最差的。而PSO_ΜDBN 模型和CC-PSO-DBN 模型的稳定性,在正常蛋和变质蛋的检测中各有优劣,而在随机蛋的检测中CC-PSO-DBN模型的稳定性则要好于PSO_ΜDBN模型。
5 结论
本文对QPSO算法的收敛特性进行了分析,粒子势阱长度的变化越大,粒子寻优能力越强,相反则越弱,进而可以通过粒子势阱长度变化率控制来避免粒子早熟,提升QPSO 算法的收敛精度。改进方法采用对粒子平均最优位置计算中,粒子自身最优位置所占比重进行优化,以粒子相近两代迭代中势阱长度变化率的比重作为粒子平均最优位置计算中的权重,来调节粒子势阱长度。最后建立了蛋黄形状检测LQ_DBN 模型,通过检测蛋黄的形状判别鲜蛋是否变质。在模型构建过程中,利用QPSO 算法的全局寻优能力优化了DBN 网络模型的参数,获得更精确的蛋黄形状检测模型。由最后的实验结果可知,LQ_DBN、CC-PSO-DBN、PSO_ΜDBN 和原始DBN四个模型对蛋黄形状的检测识别率都达到了很好的效果,其中以本文的LQ_DBN 模型检测识别准确率最高,且模型的检测稳定性也最好。
