弹性机构的动态应力研究

2021-05-26刘晓静

山西冶金 2021年2期

刘晓静

（山西工程职业学院，山西太原030009）

早前对运动机构的研究局限于其刚性分析，对其弹性变形对工作性能及可靠性的影响考虑甚少。随着工业的不断发展，机构的弹性变形对机构的影响日益增加。现有国内外很多学者研究弹性机构的动力学分析。Howell[1]和Midha提出伪刚体模型，奠定了弹性机构的研究的基础。HETRIK[2]等研究了弹性机构的拓扑优化设计方法的重要性。张义民[3]则提出了机械动态与渐变可靠性理论。

弹性机构运动过程中，构件上任一点的应力应变会随着时间的变化而发生改变。因此对运动中的弹性杆件的动态应力应变分析对后续系统可靠性分析具有重要的意义。

1 弹性连杆机构动态应力

物体受到外力作用下会发生一定的变形，变形后线段伸长或缩短的值与原长的比值成为应变，即：

式中：L为变形前的长度；ΔL为其变形后的伸长量。

以梁单元横截面作为研究基础，点Q是梁单元中的任意一点，并设该点属于第i个梁单元点Q处的应变可由该点的弯曲应变和拉压应变[4]的叠加得到，因此点Q的总应变可以表示为：

式中：ε为点Q的总应变；ε1为第i个梁单元弯曲变形引起Q点处的应变（弯曲应变）；ε2为第i个梁单元拉伸变形引起Q点处的应变（拉伸应变）。

由于在弯曲过程中，中性层的长度不发生变化，根据式（1）的定义，中性层处的应变[5]为：

根据胡克定律：

将式（3）代入（4）中得：

假定单元AB发生变形后移至A*B*，取AB上的一个微单元CD，设定长度为dx，则CD两点的坐标为（x，0）、（x+dx，0）。当梁单元发生变形后，CD的位置变为C*D*，其中C点的纵向位移和轴向位移分别为SW、SV，所以单元局部坐标C*系中坐标为（x+SW，SV），D*点坐标为

线性单元C*D*的拉伸应变[6]为：

2 算例

主动杆件转速为300 r/min，下页图1为弹性四杆机构曲柄与连杆的中点模型结构，机构参数见表1。

表1 弹性四杆机构的参数 mm

下页图2为计算弹性四杆机构在不同时刻的最大动应力的分析流程图。

将机构参数代入动态应力的计算公式中，可以得到弹性四杆机构曲柄与连杆中点的最大动应力随着主动杆件转动角度的曲线如图3和图4。

图1 曲柄与连杆中点弹性位移

图2 不同时刻最大动应力分析流程图

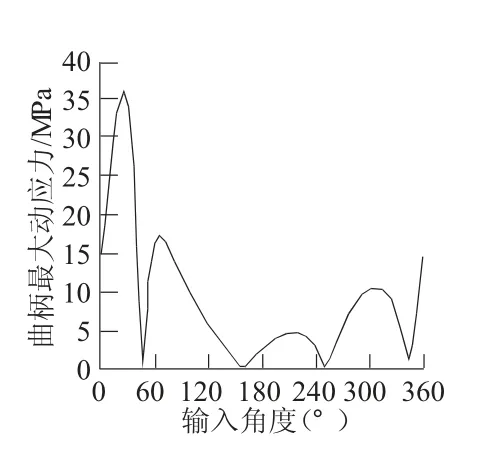
图3 曲柄中点最大动应力

图4 连杆中点最大动应力

从图3，图4中可以看出，随着主动杆件转角的改变，曲柄和连杆的动态应力随之改变，但杆件不同的点处的整个运动过程中最大动应力的变化趋势不完全一致，因此在研究整个系统最大动应时需要计算各点处的最大动应力进行比较得到。从图中可以看到在角度为由于机构刚启动，曲柄和连杆中点动态应力具有较大的波动，并达到整个过程中的最大值，且曲柄中点的最大动应力明显大于连杆中点的最大动应力。