LNG 储罐高真空多层绝热传热计算模型分析研究
2021-05-25李延娜邓育轩匡春燕张艳丽
李延娜 邓育轩 匡春燕 徐 菁 张艳丽
(兰州城市学院培黎石油工程学院,甘肃 兰州730070)
1 概述
城市中天然气的用量随着时、日、月均会发生变化,因此,城市中天然气的使用存在着日不均匀性、时不均匀性、季节不均匀性,必须采取相应的方式来调节均匀供气和不均匀耗气之间的矛盾,也就是必须对天然气进行调峰[1]。一般情况下,常见的天然气调峰方式主要有:用输气管末段调峰、用储气罐调峰、用地下储气库调峰、用高压管束调峰、用液化天然气(Liquefied Natural Gas,简称LNG)调峰,不同的调峰方式适用于调节不同的不均匀工况[2]。用LNG 调峰是在LNG 调峰站中安装LNG 储罐储存LNG 来进行调峰,具有容量大、站址选择相对容易、投资少、建设周期短、不易受污染等优点[2-7],受到了广泛关注。但与此同时,LNG 沸点较低,通过绝热层的较少漏热量都会造成LNG 储罐一定量的蒸发损失,因此,必须选择优良的绝热形式,以降低LNG 储罐蒸发损失。目前,高真空多层绝热是LNG 储罐一种较理想的绝热形式,可以有效减小通过绝热层的漏热量,进而降低LNG 储罐蒸发损失。
本文介绍LNG 储罐高真空多层绝热常用的两种传热计算模型,Lockheed 传热计算模型和Layer-by-Layer 传热计算模型,分析这两种传热计算模型的共同点和不同点,说明这两种传热计算模型的特点,为LNG 储罐高真空多层绝热传热计算模型的合理选用提供一定依据。
2 Lockheed 传热计算模型[8]
采用Lockheed 传热计算模型计算LNG 储罐高真空多层绝热传热量时,将整个绝热层中的传热过程看作一维稳态传热,同时认为在整个绝热层中主要存在辐射换热、气体导热、固体导热三种热交换形式。此外,Lockheed 传热计算模型以整个绝热层为研究对象,基于绝热层的总厚度及层密度,分别计算整个绝热层中的辐射换热量、气体导热量、固体导热量,最终得到整个绝热层的总传热量。具体计算过程如下:

2.1 整个绝热层中的辐射换热量q辐射换热:如式(1)所示。
式(1)中,B 为经验参数;ε 为辐射层的发射率;σ 为玻尔兹曼常数;TH为热端温度,K;TC为冷端温度,K;NS为辐射层层数(NS=N*·δ,N*为绝热层层密度,δ 为绝热层总厚度)。
2.2 整个绝热层中的气体导热量q气体导热:如式(2)所示。
式(2)中,C 为经验系数;m 为经验指数;P 为夹层真空度,Pa。
2.3 整个绝热层中的固体导热量q固体导热:如式(3)所示。

所以,Lockheed 传热计算模型计算得到的LNG 储罐高真空多层绝热总传热量q总为:

根据式(4)可知,采用Lockheed 传热计算模型计算LNG 储罐高真空多层绝热传热量时,只需知道绝热层的总厚度及层密度,就可以计算出整个绝热层的总传热量。
此外,从式(1)~式(3)可以看出,利用Lockheed 传热计算模型可以得到LNG 储罐高真空多层绝热整个绝热层中的辐射换热量、气体导热量、固体导热量,但不能具体得到每相邻两辐射层之间的辐射换热量、气体导热量、固体导热量。
3 Layer-by-Layer 传热计算模型[9,10]
Layer-by-Layer 传热计算模型也将LNG 储罐高真空多层绝热中的传热过程看作一维稳态传热,即认为在LNG 储罐高真空多层绝热中,热量只沿绝热层厚度方向发生传递,同时也认为在LNG 储罐高真空多层绝热中,相邻两辐射层之间主要存在三种形式的热交换,分别是:相邻两辐射层之间的辐射换热、相邻两辐射层之间剩余气体的导热、相邻两辐射层之间经间隔物进行的固体导热。Layer-by-Layer 传热计算模型就以这相邻两辐射层为研究对象,采用假设法及迭代法计算相邻两辐射层之间的辐射换热量、气体导热量、固体导热量,进而得到整个绝热层的总传热量。具体计算过程如下:
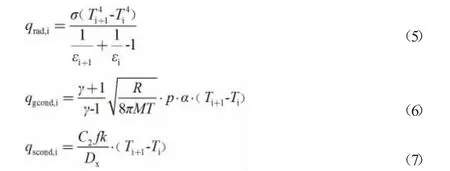
3.1 相邻两辐射层之间的辐射换热qrad,i:如式(5)所示。
式(5)中,σ 为玻尔兹曼常数,5.675×10-8W/(m2·K4);Ti+1、Ti分别为相邻两辐射层的温度,K;εi+1、εi分别为相邻两辐射层的发射率。
3.2 相邻两辐射层之间剩余气体的导热qgcond,i:如式(6)所示。

3.3 相邻两辐射层之间经间隔物进行的固体导热qscond,i:如式(7)所示。

最后,采用数学编程软件对LNG 储罐高真空多层绝热整个绝热层的总传热量qtot,i进行编程计算。计算时,首先假定LNG储罐高真空多层绝热第1 层辐射层,也就是从冷端到热端的第1 层辐射层温度为T1=TL+C1,TL为冷端温度,即LNG 储罐内罐外壁面温度,C1为一常数,与此同时,将LNG 储罐内罐外壁面看作一层辐射层,于是根据TL和T1值以及式(8)就可以求出LNG 储罐内罐外壁面与其高真空多层绝热第1 层辐射层之间的传热量q1,由于之后相邻两辐射层之间传热量相等,即q1=q2=……=qn,n 为辐射层层数,所以根据式(8),可反算出之后每一层辐射层的温度T2、T3、……、Tn,比较计算出的Tn与TH,TH为热端温度,即LNG 储罐所处外界环境温度,若Tn与TH两者差值小于等于要求值C2,则假设成立,即可得出LNG 储罐高真空多层绝热整个绝热层的总传热量qtot,i,若Tn与TH两者差值大于要求值C2,则假设不成立,需重新假设T1,直到Tn与TH两者差值小于等于要求值C2,计算才结束。具体迭代过程如图1 所示。

图1 Layer-by-Layer 传热计算模型的具体迭代过程
从整个计算过程可以看出,采用Layer-by-Layer 传热计算模型不仅可以得到LNG 储罐高真空多层绝热整个绝热层的总传热量,还可以得到绝热层中每层辐射层的温度,然后基于这些温度,又可以得到LNG 储罐高真空多层绝热每相邻两辐射层之间的辐射换热量、气体导热量、固体导热量。
4 结论
4.1 Lockheed 传热计算模型和Layer-by-Layer 传热计算模型都将LNG 储罐高真空多层绝热中的传热过程看作一维稳态传热,且都认为在LNG 储罐高真空多层中主要存在辐射换热、气体导热、固体导热三种热交换形式。
4.2 Lockheed 传热计算模型以整个绝热层为研究对象,基于绝热层的总厚度及层密度,计算整个绝热层中的辐射换热量、气体导热量、固体导热量,最终得到整个绝热层的总传热量;Layer-by-Layer 传热计算模型以相邻两辐射层为研究对象,采用假设法和迭代法逐层计算相邻两辐射层之间的辐射换热量、气体导热量、固体导热量,进而得到整个绝热层的总传热量。
4.3 采用Lockheed 传热计算模型计算LNG 储罐高真空多层绝热整个绝热层的总传热量相对简单,但无法得到其它相关参数。
4.4 采用Layer-by-Layer 传热计算模型除了可以得到整个绝热层的总传热量,还可以得到绝热层中每层辐射层的温度以及每相邻两辐射层之间的辐射换热量、气体导热量、固体导热量。
