滴流床反应器床层液体分布GWO-RFR模型的研究与优化
2021-05-25延会波李立毅
延会波,张 玮,李立毅,翟 剑
(太原理工大学 化学化工学院,山西 太原 030024)
滴流床反应器是一种气液并流向下通过催化剂床层的固定床反应器,广泛应用于石油和化工领域。 床层液体分布均匀性是影响其性能的主要因素。 液体分布不良会导致催化剂利用率低或过早失活,并引起局部热点和沟流、壁流等现象[1]。 因此,准确地预测和优化床层液体分布成为滴流床反应器设计和放大的重要问题。
针对滴流床床层液体分布问题,收集器法[2]和各种可视化成像技术[3-7]是主要的实验研究手段,但往往受到操作、几何和物理条件的限制,且通常是耗时和昂贵的。 为此,国内外研究人员开始探索使用计算流体力学(CFD)来模拟滴流床床层结构,并对床层液体分布进行分析,常用的CFD模型如三相欧拉模型[8]、多孔介质模型[9]。 滴流床床层多相流动是复杂的,建立精确的数学模型对床层液体分布进行分析是困难的,且CFD分析需要大量的计算,模拟结果容易受划分网格的质量和数量影响,模拟的计算成本很高。 因此,使用一种简单、经济和高效的方法来研究滴流床床层液体分布具有现实意义。 随着人工智能技术的发展, 数据驱动建模开始兴起,机器学习在滴流床反应器的研究中取得了突破性应用[10,11],Bazmi等[2]采用神经网络建立了滴流床床层液体分布模型。 然而由于神经网络基于经验风险最小化原理,往往存在过学习和低泛化问题[12]。近年来兴起的随机森林回归(RFR)模型从原始样本中随机选取训练样本和特征来构建不同的决策树,大大降低了过拟合的风险,在建模精度和泛化能力方面也都优于神经网络模型。
本研究的主要目的是基于RFR开发准确可靠的滴流床床层液体分布模型,并用灰狼优化(GWO)算法优化了RFR的超参数。 此外,对影响床层液体分布的关键特征(床层特性参数和操作参数)进行了重要性排序。 最后,以该模型作为代理模型,采用粒子群算法优化了滴流床的操作参数,可为床层液体分布的优化提供指导。
1 RFR模型与GWO算法
1.1 RFR模型
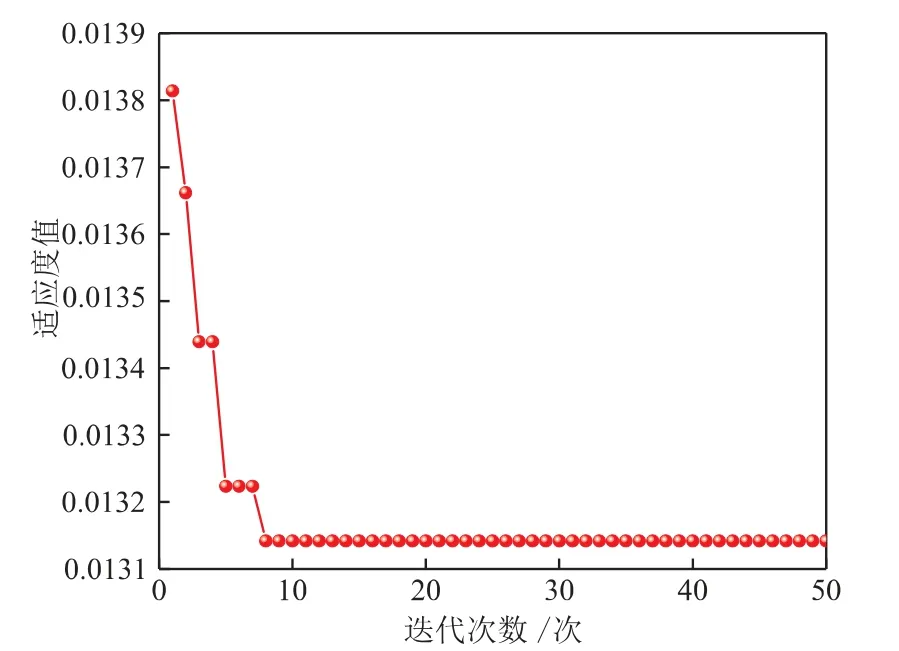
RFR模型是Breiman于2001年提出的一种集成学习算法[13],可以用于处理回归、分类和特征选择等问题。给定一个训练数据集S={xi,yi}N,(X,Y)∈RM*R,输入矩阵X包含M个特征和N个样本,Y为目标向量。RFR模型在原始训练样本中有放回抽取多个与原始样本数量相等的训练子集Sk(k=1,2,...,ntree)。 每个训练子集构建一个决策树。 在建立单棵决策树时, 每个非叶子节点都从M个特征中随机选择mtry(mtry RFR生成训练子集时,原始训练集中大约2/3的样本被抽取,称为袋内数据,其余1/3未被抽取的样本称为袋外数据(OOB)[15]。 在建立RFR的过程中,根据OOB特征加入噪声前后模型预测精度的降低程度[16]来对特征的重要性排序。 模型的预测精度变化用OOB均方误差(MSE)平均递减值来衡量,MSE的定义如下: 式中,n为袋外数据的个数;yi为袋外数据的实际值;f(xi)为袋外数据的预测值。 本研究中将各个特征xi的MSE平均递减值定义为hi,将hi的绝对值进行归一化,得到特征xi的影响权重为: 式中,wi为每个特征的影响权重。 RFR超参数的选取对于提高模型性能至关重要。 目前普遍采用先验知识或人工调整确定,往往无法获得满意的效果。GWO算法是一种模拟灰狼狩猎行为的新型群智能优化算法。 该算法具有简单、收敛速度快、参数设置少等优势。因此,采用GWO算法对RFR的超参数寻优。 在该算法中,根据灰狼的领导等级制度, 将灰狼划分为α、 β、 δ和ω 4个等级[17],如图1所示。 α是狼群的领导者,主要负责决定狩猎、 作息时间等; β和δ负责协助和传达α的决策;其余的灰狼ω被用来平衡狼的内部关系, 服从上级狼的管理和决策。 此外,灰狼狩猎的三个主要阶段包括猎物搜索,猎物包围和攻击。 图1 灰狼的领导等级 在优化过程中,假设灰狼数量为N,搜索空间为d维,灰狼的位置表示为Xwi= [xi1,xi2,…,xid],α被认为是最优解,其位置由Xα表示。 然后,β和δ分别为次优解和第三优解,它们的位置分别由Xβ和Xδ表示。其余的ω代表待选解。 灰狼狩猎过程的包围策略如公式(3)和(4)所示: 式中,t为当前迭代次数;和为系数向量;和分别代表猎物和狼的位置。 和系数向量按公式(5)、(6)计算: 式中,随着迭代次数的增加,从2线性减少到0;r1和r2为[0,1]之间的随机数。 灰狼α、 β、 δ具有有关猎物的最佳信息,其余的灰狼ω根据三者的位置来更新各自的位置, 如公式(7)~(9)所示: 式中,i为1、2、3;j为分别为灰狼α、β、 δ与灰狼ω之间的距离。 针对RFR模型超参数确定困难的问题,本文采用GWO算法优化模型的超参数, 提出一种GWORFR模型,其算法流程如图2所示。 图2 GWO-RFR算法流程 GWO-RFR模型的基本步骤如下: (1)根据随机抽样技术,随机选取80%的数据为RFR的训练集,剩余20%的数据为测试集; (2)参数设置和初始化灰狼种群,参数包括灰狼数量N、最大迭代次数lmax; (3)灰狼的适应度值计算和排名。 公式(10)中,训练集的均方根误差(RMSE)用来评估每个灰狼的适应度值。根据适应度大小,对灰狼进行排名。排名前三的灰狼分别是α、β和δ; 式中,n为预测点的个数;yi为实际值;f(xi)为预测值。 (4)采用公式(5)和公式(6)更新参数a、和; (5)根据公式(8)和公式(9)更新灰狼α、β和δ其余灰狼的位置; (6)如果算法未达到最大迭代次数,则返回步骤(3),否则,算法结束,输出优化结果; (7)采用上述步骤获得的最优解训练RFR模型,并对该模型进行评估。 影响滴流床床层液体分布的因素主要包括物性参数、床层特性参数和操作参数等。 从公开发表的文献[2,18-20]中提取了328组冷态实验数据,具体数据来源与实验条件如表1所示。 表1中,气相为氮气或空气,密度和黏度相近,液相均采用水,所以忽略物性参数的影响。 在建模过程中,选取了2个操作参数和3个床层特性参数为输入特征, 分别为气液表观速度ug和ul、床层高度H、反应器直径与颗粒直径比D/dp和床层平均孔隙率ε,各特征取值范围:ug为0~0.16 m/s,ul为0.0017~0.0430 m/s,H为100~1300 mm,D/dp为100~150,ε为0.41~0.46。 表1 滴流床液体分布的实验数据与条件 选择液体分布不均匀度Mf为目标输出。Mf是为定量表征床层的液体分布而引入的评价指标。 根据文献[18]定义如公式(11)所示: 式中,QLi为第i个区域的液体流量;N为收集器划分区域的个数;Qmean为各个区域的平均流量;Mf处于0和1之间,0表示各区域液体流量相同, 为最理想液体分布,1表示液体全部流入某一个区域,为最差液体分布。 在本研究中, 建立GWO-RFR模型的目的是找到满足输入特征和目标输出映射关系的函数关系式,具体如公式(12)所示。 建模时将328组实验数据随机划分为训练集和测试集。 其中,263组数据用于RFR模型训练,65组数据用于评估模型的性能。 RFR模型建模时,其中需要控制的超参数主要是决策树棵数ntree和随机选择特征个数mtry, 默认值分别为ntree= 500和mtry=M/ 3,M为特征数。在GWO算法中,设置灰狼数量N为30,最大迭代次数lmax为50,超参数范围分别为ntree[1,500],mtry[1,5]。图3为适应度值随迭代次数的变化曲线。 由图3可以看出,适应度值随迭代次数的增加而降低,在第10代左右收敛,50次迭代后达到最小,为0.01314,此时对应的(ntree,mtry)为(32,5)。 图3 适应度值随迭代次数的变化 为了评估GWO-RFR模型的性能,考虑了三个评价指标,分别为平均绝对百分比误差(MAPE),均方误差(MSE),相关系数(R2)。其中,R2代表模型的可解释性, 值在0到1之间;MSE和MAPE反映样本数据的离散程度,值越低说明精度越高。按照如下公式定义: 式中,n为预测点的个数;yi为实际值;f(xi)为模型的预测值;为实际值的平均值;为预测值的平均值。 为了验证该模型的准确性, 将GWO-RFR模型预测结果和实验结果对比,结果如图4所示。 图4中,红球表示GWO-RFR模型对训练样本的预测结果,黑球是模型对测试样本的预测结果。 可以看出,训练集和测试集数据都在对角线y = x附近均匀分布,意味着GWO-RFR模型预测值和实验值取得了良好的一致性。测试样本的R2为0.969,MSE和MPAE分别为0.00048和7.10%,与训练样本预测效果相近,表明该模型具有良好的泛化能力,可以作为一种新方法来处理滴流床床层液体分布不均匀度Mf与操作参数、床层特性参数之间的复杂非线性关系。 图4 GWO-RFR模型预测结果与实验结果对比 在滴流床床层液体分布模型中,对输入特征重要性程度的量化可以为床层液体分布的精准预测和优化提供指导。 在这项研究中,使用GWO-RFR模型的OOB均方误差的平均递减值对5个特征的重要性进行评估。模型特征重要性排序如表2所示。由表2可知,气体表观速度是与滴流床床层液体分布高度相关的特征,对床层液体分布影响最大,影响权重为48.12%;反应器直径与颗粒直径比对床层液体分布影响最小,影响权重仅为2.23%;液体表观速度和床层平均空隙率是相对重要的。 另外也可以看出,相对于床层特性参数,操作参数对床层液体分布的影响更大。 当滴流床床层出现液体分布不均时,首先考虑调节操作参数来改善液体分布。 表2 特征重要性排序 在实际工程运用中,床层特性参数一般固定不变,通常调节两个操作参数使床层液体分布状态达到最优。 基于GWO-RFR模型, 采用粒子群优化(PSO)算法建立了滴流床床层液体分布操作参数优化模型,优化流程如图5所示。 图5 基于GWO-RFR模型的PSO优化流程 PSO算法是一种模仿鸟群觅食行为的群智能寻优算法。PSO首先在可行解空间随机生成一群粒子,然后根据适应度值迭代寻找最优解。 该算法以实现容易、精度高、收敛快等优点被广泛应用于各个工业领域的参数优化当中[21]。 采用PSO对滴流床床层液体分布的操作参数优化时,设置初始种群大小为50,最大代数为50,学习因子c1和c2分别为1.5和1.7,GWO-RFR模型作为PSO的适应度函数。 表3为三种床层特性参数条件下,GWO-RFRPSO优化模型获得的最小Mf与文献[2,19]最小Mf的对比结果。 由表3可知,不同的床层特性参数下,采用GWO-RFR-PSO优化模型获得的Mf比文献[2,19]最优结果对应的Mf更小,表明该模型是有效的,可用来优化滴流床的床层液体分布。 表3 优化结果和文献最优结果对比 (1)提出了一种GWO-RFR滴流床床层液体分布模型。 测试样本的R2、MSE和MAPE分别为0.969、0.00048和7.10%,该模型预测精度高,泛化能力强。 (2)影响滴流床床层液体分布的特征重要性排序为:气体表观速度、液体表观速度、床层平均空隙率、床层高度、反应器直径与颗粒直径比。 (3)基于GWO-RFR代理模型,采用PSO优化了滴流床的操作参数,有效地降低了床层液体分布不均,为滴流床床层液体分布的优化提供了一种新的思路。

1.2 GWO算法

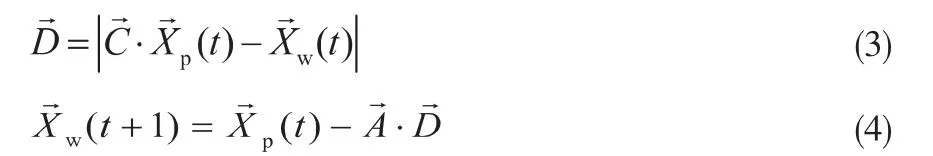


1.3 GWO-RFR模型

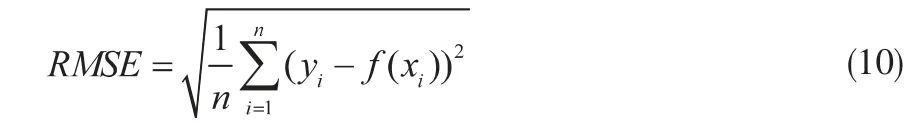
2 基于GWO-RFR的滴流床床层液体分布预测模型
2.1 建模数据来源


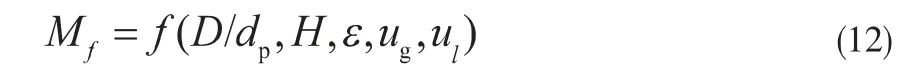
2.2 模型参数优化
2.3 模型评估

3 结果与讨论
3.1 GWO-RFR模型预测结果与实验结果比较
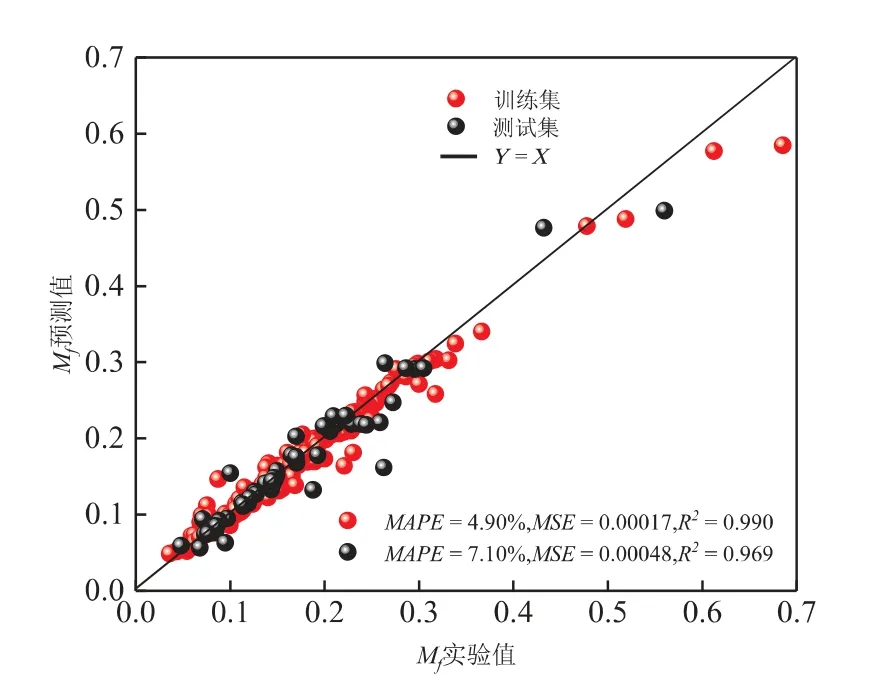
3.2 模型特征重要性分析
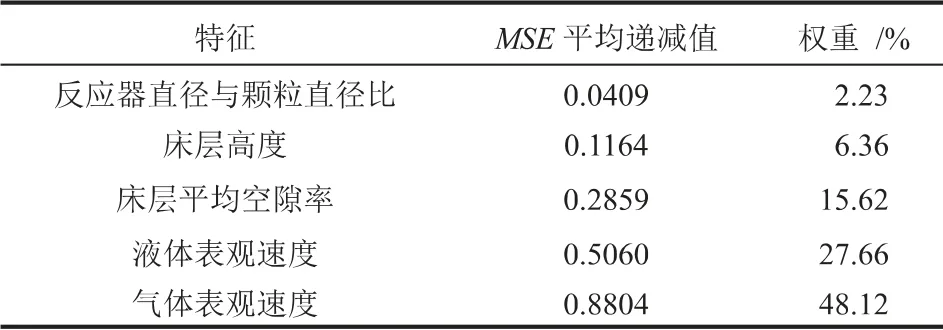
3.3 模型操作参数的PSO优化

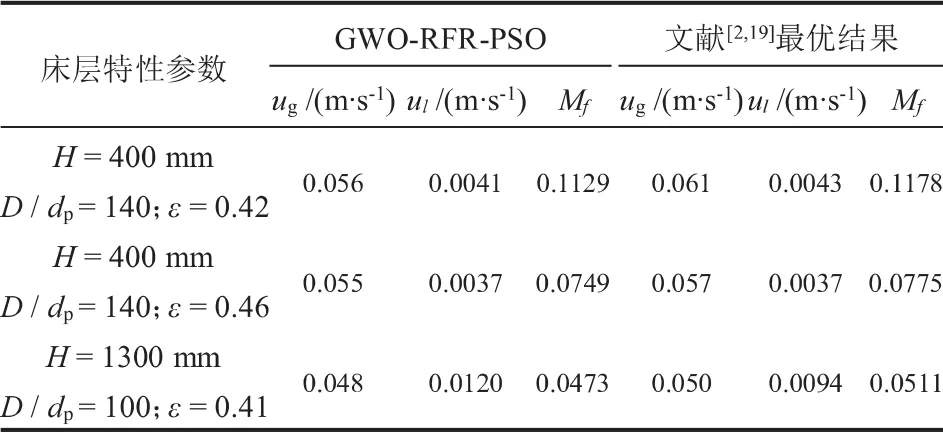
4 结论
