智能物流下货到人模式的货位分配优化
2021-05-25何利力
徐 铨,何利力
(浙江理工大学信息学院,浙江杭州 310018)
0 引言
随着物联网技术的发展,智能物流运用物联网、互联网、自动化、人工智能等技术实现了物流的智能化、自动化,包括智能仓储、运输管理、物流管理等[1]。自动导航车(Automated Guided Vehicle,AGV)作为智能仓储货架搬运方式[2],能实现运输路线的数字化管理及智能路线规划。
货位分配策略是智能物流仓储的重要决策问题,几乎影响着所有关键的仓储作业过程,包括拣货、生产效率、货物定位和装箱打包等。它决定货物的存储位置,影响货物库存盘点和跟踪,直接决定货物出入库效率。货位分配原则主要有:周转率原则、货物相关性原则、稳定性原则等[3]。货物货位分配策略主要有随机分配、固定分配、分类分配、共享分配策略[4]。Housman 等[5]研究了随机存储、就近存储以及基于周转率分类策略对自动仓储操作性能的影响;文献[6-8]分别从库存周转率、分类随机策略、COI 指数策略研究货位分配优化。
针对仓库货位分配优化研究,段悦等[9]提出一种基于入侵杂草算法的货位分配方法;钱同惠等[10]提出用等效标号法优化分配策略;张贵军等[11]提出一种基于精英多策略差分进化算法的货位分配方法;赵阳[12]提出一种双种群遗传算法并将其应用于立体仓库货位分配;李珍萍等[13]设计一种贪婪算法并验证算法的有效性;彭小利等[14]研究制造物联技术环境下智能仓库货位优化;宁方华等[15]研究一种针对货到人模式下的鱼骨型布局的禁忌搜索算法,缩短了拣选路程;徐伟华等[16]利用遗传算法对密集型自动化立体仓库货位进行优化;陈月婷等[17]提出基于Pareto 的粒子群优化算法解决货位分配问题;Li 等[18]提出一种基于改进遗传算法的货位分配优化算法。
现有研究有的只考虑单个原则,有的研究目标是静止的立体化自动仓库,有的多目标求解优化算法存在收敛速度慢等问题。本文拟对智能物流下货到人模式的货位分配问题进行研究,以稳定性、周转率、相关性为目标建立智能物流仓库的多目标货位分配模型,并提出一种改进的遗传算法对模型进行求解,算法通过改进初始化方式、选择算子、交叉算子、变异算子提高收敛速度,避免陷入局部最优解。
1 模型构建
1.1 智能物流仓库
智能物流仓库是智能物流过程的重要环节,应用物联网技术,构建智能仓库,实现仓库状态实时感知。借助射频识别技术(RFID)、二维码、传感器及互联网将仓库里的货架、货物、货位、托盘、AGV 等物理实体智能化,使其成为具有自身信息反馈功能的智能对象[19]。智能仓库主要采用自动立体化仓库或基于AGV 的移动式货架仓库,本文研究对象为基于AGV 的移动式货架仓库。
假设智能仓库只有一个出入库位置,货架位置呈正方形,一个位置放置一个货架,货架和位置存在一对一的对应关系(图1 中一个正方形上可以放置一个货架)。出入库点、货架位置用(x,y)表示,出入库点位置为(0,0)。仓库布局如图1 所示。

Fig.1 Warehouse layout图1 仓库布局
1.2 基本条件假设
为方便数学建模及问题求解,本文作出以下假设:
(1)两排货架之间有一道巷道,每条巷道宽为w,布局如图1 所示。
(2)仓库内货架尺寸、货位相同,长a。
(3)货架上的每层货位最多只能放置一种货物。
(4)每个货架放置于仓库的位置固定,即货架每次被AGV 小车搬运后仍回到原来位置。
(5)AGV 小车在行驶过程是匀速运动,速度恒定为v。
(6)AGV 小车搬运货架出入库按照最短路径搬运。
(7)不考虑多AGV 小车协同工作情况。
1.3 货位分配模型
1.3.1 货架稳定性原则
为保证货架稳定性及AGV 小车运输过程平稳,要求货架重心尽量低,即重的货物放于靠近地面的低层货位,轻的货物放于远离地面的高层货位。货架重心评价指数可用货物质量与当前所在层数的乘积表示,乘积越小表示重心越低。由此建立的数学模型如式(1)所示。
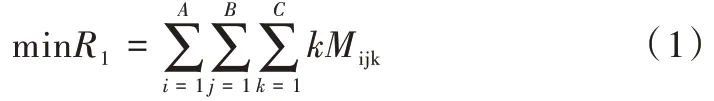
约束条件为:

其中,A为仓库货架总排数,B为仓库货架总列数,C为货架总层数;Mijk第i排第j列货架上第k层货物的质量。
1.3.2 出入库效率原则
智能物流货到人模式中,AGV 搬运速度是恒定的,搬运货物的效率与搬运距离有关。同时,为了提高货物出入库效率,采用基于周转率的货位分配策略,将周转率高的货物放在靠近出入库点的货架上。周转率为一段时间内货物出入库数量和该货物总量的比值。由此建立的数学模型如式(2)所示。
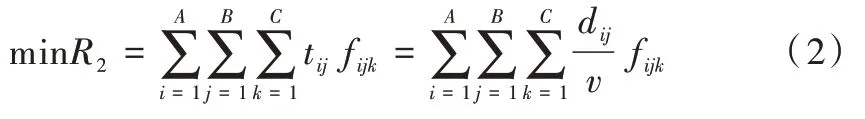
其中,tij表示AGV 小车将第i排第j列的货架运到出入库点所需时间,dij表示第i排第j列货架到出入库点的运输距离,fijk第i排第j列货架的第k层上货物的周转率。
仓库布局近似看作直角坐标系,出入库位置为原点(0,0),货架位置为(i,j),从而得到AGV 小车运输货架到出入库点的最短距离如式(3)所示。
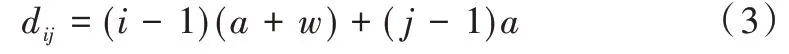
将式(3)代入式(2)得到最终函数如式(4)所示。

约束条件为:
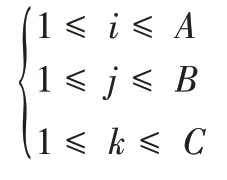
1.3.3 货物相关性原则
实际环境下当一种货物出库,往往相关的货物也需要一起出库。因此相关性大的物品进行入库货位分配时,应靠近存放,即两货物所在货架之间距离应当较小。货物相关性用相关度进行衡量,两种货物相关度越高表示越相关。货物相关度计算如式(5)所示。

其中,Pij表示货物i、j之间的相关度,Oi表示包含货物i的订单数量,Oj表示包含货物j的订单数量,Oij表示包含货物i和j的订单数量。设定一个阈值,当小于阈值则两个货物相关组成一个相关组。
假设两货物分别放置在(i1,j1,k1)和(i2,j2,k2),则目标函数如式(6):
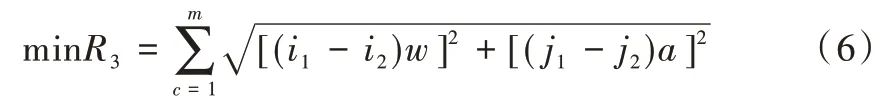
约束条件为:
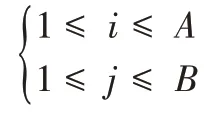
其中,c表述相关物品的组序号,m表示相关货物的组数。当i1=i2表示两个货物在同一货架上。
1.3.4 多目标分配模型
当对货物货位进行分配时,需考虑上述几个原则,即满足式(1)、式(4)、式(6)3 个方程。
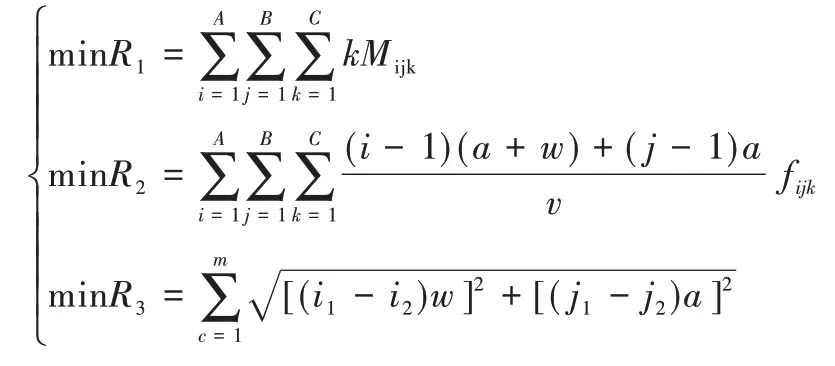
约束条件为:
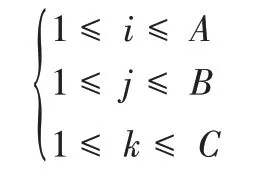
根据式(1)、式(4)、式(6)对货位优化问题进行求解,该问题求解是多目标函数求极值,本文用权重法为3 个函数分别分配θ1、θ2、θ33 个权重因子,将多目标函数转为单目标函数进行求极值。单目标函数如式(6)所示。
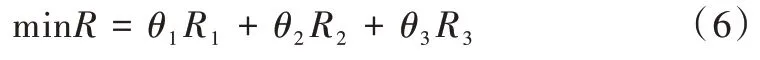
约束条件为:
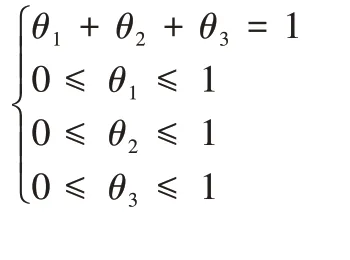
2 遗传算法
已经根据3 个原则建立多目标数学模型,并利用权重法转换成单目标函数。本文将基于改进的遗传算法求解该模型。
遗传算法(Genetic Algorithm,GA)是一种模拟生物种群进化的搜索算法,由美国大学教授Holland[20]提出。遗传算法的基本原理是:首先初始化设置一定数量个体(染色体)组成的生物种群,每个个体代表一个潜在的解;每个个体通过适应度评价进行优胜劣汰,选择较优个体经过交叉算子、变异算子操作形成下一代种群,经过种群多次进化,种群会逐渐向最优个体进化;当进化结束,得到最优个体。算法流程如图2 所示。

Fig.2 Genetic algorithm process图2 遗传算法流程
2.1 染色体编码
遗传算法的模拟过程都是基于染色体编码的操作。因此编码方式对算法性能有较大影响。相比二进制的编码方式,用自然数编码表达更加直观。本文采用自然数编码方式,染色体编码方式:x1x2x3...xn...xm,1 ≤n ≤m,其中n为待入库货物数量,m为空闲货位数量。每条染色体表示一种货位分配结果,每条染色体可以分为多个基因x,基因表示一个货架货位的位置(i,j,k),以坐标形式表示仓库内货架的空闲货位位置,i、j、k3 个整数分别表示货位在i排第j列货架的第k层。
若i、j、k都小于10,则基因可以用三位数表示。当有3个货物待入库和4 个空闲货位时,第一个货物放在(1,1,1),表示货物放在第1 排第1 列货架第1 层;第二个货物放在(1,1,2),表示货物放在第1 排第1 列货架第2 层;第二个货物放在(1,1,3),表示货物放在第1 排第1 列货架第3 层,剩下的货位(2,1,1) 未分配货物。此时,染色体编码为“111112113211”,表示一种货位分配解。
2.2 初始化种群
初始化种群的基本内容是随机生成一定数量的个体作为遗传算法的初始种群。初始种群对算法收敛效率和最优解的优劣有较大影响,选择合适的初始种群很有必要。本文采用先获取空闲货位的坐标数据,周转率高的货物分配到靠近出入库点的货位,生成初始染色体,然后随机选择两个货位进行交换,重复操作得到新染色体,不断循环初始化第一代种群。在种群规模选择上,同时兼顾计算效率和种群多样性,本文取种群规模100 左右。
2.3 适应度函数
适应度函数是判断个体优劣程度的重要评价标准。根据适应度大小对个体进行优胜劣汰,适应度越大的个体遗传到下一代的概率更大,适应度越小的个体遗传到下一代的概率更小。本文用式(6)表示适应度函数。
2.4 选择算子
选择算子是模拟大自然生物进化的淘汰过程。通过适应度函数计算当代所有个体适应度,选择优质个体进入下一代种群。本文选择精英选择策略,选择适应度最优的个体直接进入下一代;种群剩余个体从经过交叉、变异的个体中产生。
2.5 交叉算子
遗传算法使用交叉算子模仿生物产生后代过程。设定交叉概率Pc,选择两个染色体个体计算交叉概率,若交叉概率小于设定概率则按照某种方案交换部分基因,生成子代个体;否则重新选择两个个体并进行判定。单纯使用个体交叉会造成数据错乱,因此本文选择模拟细胞分裂方式以产生子代:根据交叉概率判断个体是否需要分裂复制;若个体进行分裂复制,会将所有基因复制到子代并发生基因重组(交换部分基因)从而产生子代个体。
2.6 变异算子
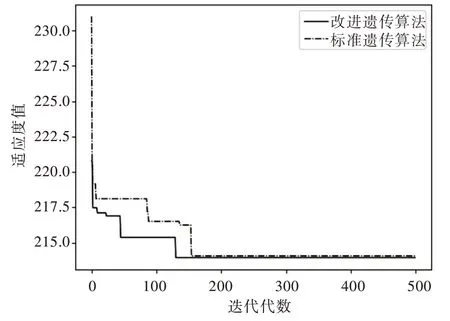
变异算子基本操作是根据变异概率确定是否改变种群个体染色体的部分基因,从而提高种群多样性,防止算法早熟收敛陷入局部最优解。本文采用交换货位位置的方式进行变异操作,首先计算生成当前个体变异概率Pi,将个体变异概率与设定的变异概率Pm进行比较,若Pi 若种群进化的迭代次数达到初始设定的迭代次数,则终止循环;否则开始选择算子并进入下一轮循环。 实验仿真数据:仓库、货架及AGV 小车基本信息如表1 所示,空闲货位信息如表2 所示。 Table 1 Basic information of shelves and AGV表1 货架与AGV 基本信息 遗传算法的参数设定:初始种群规模设为100 个,迭代代数为500 代,初始交叉概率Pc为0.8,初始变异概率Pm为0.2。实验中货物出入库效率、货架稳定性、相关货物靠近存放3 个权重视为同等重要,因此式(6)中的权重因子θ1、θ2、θ3分别设为0.33、0.33、0.33。 Table 2 Free cargo bay location information表2 空闲货位位置信息 本文选择10 件货物作为仿真数据,分别用改进遗传算法和传统遗传算法进行货位分配。货物信息(质量、周转率)及货位分配仿真结果如表3 所示。表3 中编号6 和编号13 货物为一组相关货物组。 Table 3 Inbound cargo information and distribution results表3 入库货物信息及分配结果 图3 为实验中遗传算法和改进优化的遗传算法适应度变化曲线。由图3 可以看出,对于初始种群的适应度,由于使用近货位优先分配给周转率高货物的策略,改进的遗传算法在初始阶段就远低于标准遗传算法;在此后迭代过程中,两个算法都快速收敛,但是改进遗传算法的收敛速度更快;当迭代代数至120 代左右,算法已经收敛,可以得到较好的稳定解。 Fig.3 Fitness curve图3 适应度变化曲线 针对智能物流环境下人到货模式的货位分配问题,在考虑货架稳定性、出入库效率、相关货物靠近存放的基础上,建立货位分配模型,提出一种改进的遗传算法。该算法通过优化初始种群的产生方式及细胞分裂方式进行交叉运算、变异概率阶段递减等,避免了传统遗传算法收敛速度慢等问题。实验结果表明,改进的遗传算法提高了算法收敛速度,减少了搜索时间。该方法虽然提高了效率,但仍然存在不足,需要预先设定权重因子,不同情况下需重新设定,因此如何确定权重因子值还有待研究。2.7 结束标志
3 实验与分析
3.1 实验数据与算法参数
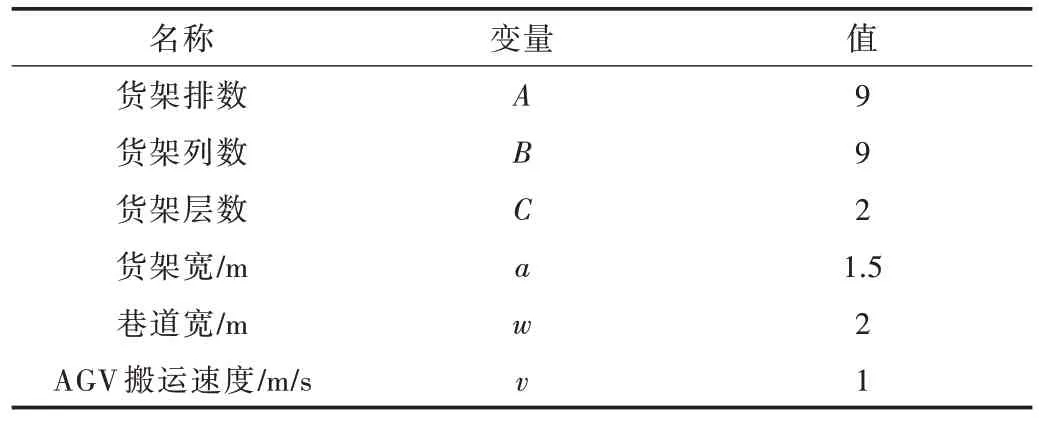
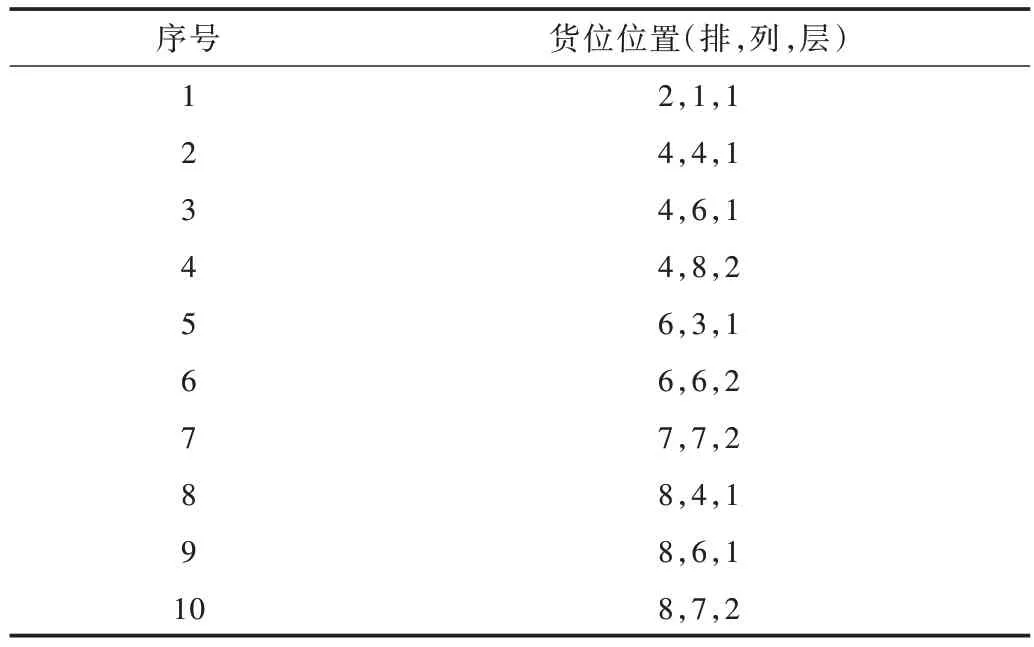
3.2 实验方案与结果分析

4 结语
