高海拔冻土地区公路路基风流场特征研究

宋正民， 马 巍， 穆彦虎， 俞祁浩， 谢胜波，3， 刘永智

（1.兰州理工大学土木工程学院，甘肃 兰州 730050； 2.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃 兰州 730000； 3.中国科学院西北生态环境资源研究院沙漠与沙漠化重点实验室，甘肃 兰州 730000）

0 引言

在区域经济发展需求推动下，伴随国家高速公路网规划的逐步实施高寒冻土区高等级公路建设已是迫在眉睫［1-3］。冻土区公路工程建设是一项世界范围内的工程技术难题，多年冻土及脆弱冻土环境给工程的修筑、运营及维护带来了极大的挑战，尤其在气候变暖背景下［4-6］。在多年冻土区，路基工程的修筑将不可避免地打破原有的地-气能量平衡，引发活动层厚度增加、多年冻土温度升高等多年冻土退化过程，进而导致路基沉降及相关工程病害问题［7-14］。为此包括块石、通风管、热管等主动冷却降温措施在冻土路基工程中得以广泛应用，通过路基结构对流换热机制与过程的调控以降低或保持下伏多年冻土地温，进而达到保证路基长期稳定性的目的［15-16］。

目前，针对块石、通风管、热管等主动冷却措施在冻土路基工程中的应用，研究人员从冷却降温机制、影响因素及实体工程降温效果等方面利用包括室内模型试验、数值模拟及现场监测等手段开展了大量研究工作并取得重要成果［17-30］。然而，已有研究工作主要关注冷却降温结构内的对流换热过程及下伏多年冻土的热响应，对于路基周边风流场特征很少关注。风流场作为复杂地气能量交换过程的重要一环，同样是冻土路基工程的关键环境边界。对于冻土区冷却路基结构而言，路基周边风流场特征显著影响着包括块石层、通风管、热管蒸发段内的对流换热机制和强度。同时，在青藏工程走廊风沙灾害日益严重的背景条件下［31-32］，路基周边风流场特征与风沙在路基周边的堆积、运移等过程密切相关，可以直接影响到块石层的边界类型（开放与封闭）、孔隙率以及通风管管内通风效率等。此外，针对拟建青藏高速公路，研究人员提出了分离式路基方案以解决宽幅沥青路面强烈吸热效应［33-35］。对于分离式路基而言，其周边风流场特征势必与整体式路基有所不同，尤其两幅路基之间风流场的相互扰动及隔离带内的湍流效应同样会影响到上述对流调控类冻土路基冷却降温机制与强度以及风沙灾害在两幅路基周边的发育过程。因此，开展路基周边风流场特征及其影响因素的研究对于冻土区路基工程的修筑、运营及维护十分必要。

针对多年冻土区对流换热类冷却路基周边风流场特征及影响因素，本文结合现场监测和数值模拟，系统开展了整体式路基周边风流场特征的研究，并考察了包括路基高度的影响规律与程度。在此基础上，针对分离式路基，研究了两幅路基并行条件下，路基周边风流场特征，并考察了中间隔离带宽度的影响。通过以上研究，以期为多年冻土区对流换热类冷却路基工程的设计、运营、维护以及青藏工程走廊风沙灾害的防治提供依据。

1 数值模拟与现场监测

1.1 物理模型

以青藏高原北麓河高速公路试验段路基结构为对象，研究高海拔地区高速公路路基周边风流场特征。其中路面宽度L为13 m，路基高度h分别为1、2、3、4、5 m。针对分离式路基，其中间隔离带宽度H分别为2、5、10、20、30、40、50 m。物理模型如图1（a）、1（b）所示，包括路基区和空气区，空气区高度为自天然地表以上30 m，宽度自路基两侧坡脚分别向外延伸60 m，模型尺寸的选取通过不同尺寸模型的试算以消除边界效应。

图1 路基风流场物理模型Fig.1 Physical models of wind flow over an embankment（a）and two separated embankment（b）

1.2 数学模型

依据已有研究成果、实测资料进行模型的参数、初始和边界条件的设定。已知青藏高原海拔4 500 m 高度处空气的运动黏度为2.73×10-5m2·s-1，年平均风速为3.0～6.0 m·s-1，主导风向主要为西北风［36］。在物理参数和边界条件的设定方面，根据青藏高原北麓河气象站、青藏高等级公路试验段现场实际情况和实测数据，选取大气压为57.7 kPa，空气密度0.737 kg·m-³，空气黏度1.75×10-5Pa·s，地表粗糙度为0.14 m［37］。模型的边界条件在左侧风入口处设置为速度入口，根据相关资料可知，风速入口在边界EH处随高度的变化可简化为：

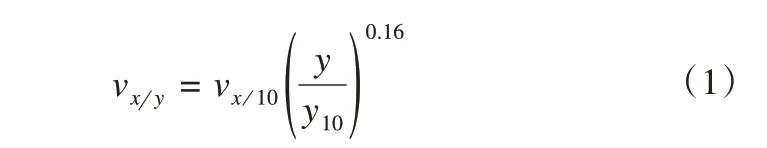
两侧面及上部空气面选用对称（symmetry）边界，右侧出口处选为质量出口（outflow）边界，地表、边坡及路基上表面为墙（wall）边界。

为更好的模拟路基背风坡处涡旋范围及涡速，采用RNG k-ε 模型。模型由Yakhot 及Orzag 提出，该模型对涡团黏度进行了修正，并在ε方程中增加了反映主流是均应变率的项。从而该模型可以更好地处理流线弯曲程度较大的流动，其控制方程为：

式中：

式中：t为时间；ρ为空气密度；k为脉动动能；Cμ取值为0.0845；ui为空气在i方向的速度分量；xj为空气沿着j方向的位移；αk为ε方程的湍流普朗特数；μ为空气动力黏度；αk、αε取值为1.39；μt为空气的湍流黏性系数；Gk为由层流速度梯度而产生的湍流动能；Gb为由浮力而产生的湍流动能；C1ϵ取值为1.42；C2ϵ取值为1.68；ε为脉动动能耗散率；YM为常量；Sk、Sε为用户定义的源项；αε为在解压缩湍流中过渡的扩散产生的波动；η0取值为4.38；β取值为0.012。

1.3 模型及参数验证

利用青藏高原北麓河高速公路试验段风流场现场监测结果与数值模拟结果开展模型和参数验证。为掌握路基周边风流场特征，在试验段路基两侧各建有风流场观测塔3 个，距离路基坡脚距离分别为60 m、30 m、0 m，观测塔高分别为3.0 m、3.0 m、4.5 m。在每个观测塔上，自天然地表向上每隔0.5 m 布设风速、风向测试传感器一组，以获取不同高度风速与风向。试验段路基高度为3.0 m，路面宽度为13 m，路基走向为东北—西南走向。图2 给出了路基左、右两侧坡脚（0 m）以及路基右侧60 m距离处的风速、风向监测装置。

图2 北麓河试验路基风流场观测系统Fig.2 Observation system of wind flow over the Beiluhe experimental-built embankment

图3 给出了2018年8月期间当风向与路基走向垂直时（东南风，面向拉萨方向自路基左侧吹向右侧）某一时刻路基左右两侧风速沿高度的分布情况。可以看出，路基左右坡脚外60 m、30 m 处环境风速自天然地表沿高度分布呈指数形式分布，与公式（1）计算结果吻合较好。同时，对比路基左侧坡脚外60 m、30 m、0 m 处同一高度处风速，可以看出坡脚处风速明显较低，反映了路基的阻挡效应。路基右侧坡脚外30 m 风速基本与路基左侧坡脚外30 m 风速沿高度分布基本一致，反映了气流扰流路基后的恢复过程。

图3 路基坡脚不同距离处数值模拟与现场实测风速沿高度分布结果对比Fig.3 Field measured and numerical simulated wind speeds vs.height at different distances away from the embankment slope foot［60 m far away from the windward slope foot of the embankment（a）；30 m far away from the windward slope foot of the embankment（b）；45 m far away from the windward slope foot of the embankment（c）；30 m far away from the leeward slope foot of the embankment（d）；60 m far away from the leeward slope foot of the embankment（e）］

以实测路基左侧坡脚外60 m 环境风速为边界条件，建立与试验段路基同尺寸物理模型，采用上节边界及参数设置，模拟路基周边风流场特征，并与实测结果进行对比，结果如图4所示。可以看出，模拟结果与实测结果有较高的吻合度，能够较好地反映风流扰流路基过程。其中路基左侧坡脚外30 m，模拟结果与实测结果仍有一定的差异，主要与该位置处微地形的起伏有关。

图4 路基周边风速（a）、风压（b）云图Fig.4 Wind speed field（a）and air static pressure field（b）around the embankment

2 模拟结果与分析

2.1 单幅路基周边风流场特征

2.1.1 单幅路基周边风流场特征区域划分

路基周边风流场特征描述利用风速、风压分布云图来描述。图4（a）给出了路基高度为3 m、路面宽度为13 m、3 m 高度处环境风速为3.5 m·s-1且风向与路基走向垂直条件下路基周边风速分布云图。依据风流绕流路基过程并结合各区域风速，可将路基两侧风流场定性划分为进风场（I）、坡前扰动区（II）、路基上部加速区（III）、坡后扰动区（IV）、出风场（V）五个区域。自风流从远场进入并靠近路基但基本不受路基影响的区域为进风场，随风流进一步靠近路基且风流场开始受路基影响直至迎风坡路肩区域为坡前扰动区（II）。风流翻越路基迎风坡后，路基顶面上部为加速区（III），自背风坡路肩直至风流场基本恢复这一区域为坡后扰动区（IV），随风流进一步远离路基且不在受路基影响后即为出风场（V）。对于对流调控类冷却路基工程以及路基风沙灾害而言，坡前扰动区、路基顶面加速区、坡后扰动三个区域内风流场特征需要重点关注。

图4（b）给出了路基周边静压云图，静压不包括大气压强，由流体微团中分子不规则运动及其具有的质量力构成，是流体微团具有的压力能和重力势能之和。对于气体来讲，气体的质量可以忽略，因此，静压主要是分子的不规则运动造成的。因此气体静压主要是单位微团气体具有的压力能。当压力变化不大，空气密度可认为是不变的，位置压差也可忽略时，空气能可由压力能（P）、动能位势能（E）三部分表示。由于空气受重力作用影响较小，因此一般忽略位势能，所以，空气初始能量相同时，速度越快，动能越大，压力能越小。当空气流过路基时，从迎风坡前起主流流管逐渐变细，流速逐渐加快，压力能逐渐减小，存在顺压梯度当空气顺迎风坡爬升至坡顶时，流管最细，流速最快，压力能最小；当空气绕过路基以后，流管逐渐变粗，流速减慢，压力能逐渐增大，存在逆压梯度

2.1.2 坡前扰动区特征及范围

从路基周边风流场区域特征来看［图4（a）］，路基坡前扰动区（II）为低风速区，即受路基阻挡II区内的风速小于同一高度下的环境风速。且由图4（b）可知，迎风坡前静压受路基阻挡，风速降低，动能减小，压力能上升，故产生高压区，且随着高度的增加，流管逐渐变细，流速逐渐上升，压力能逐渐减小。为掌握II 区的水平范围，图5（a）以路基高度3 m 为例给出了距离坡脚不同水平距离处风速沿高度的分布曲线。可以看出，受路基阻挡，坡脚处风速与同一高度下的环境风速差值随高度增加先增大后减小，其中0.5～2.0 m 高度范围内两者差值接近1.0 m·s-1，约为环境风速的30%。随着距坡脚水平距离的增加，不同高度处风速逐渐接近环境风速。以两者的最大差值不超过环境风速的10%（0.35 m·s-1）为标准，则3 m高路基条件下II区的水平范围约为15 m。随路基高度的增加，路基的阻挡效应更加显著，II区的水平范围有所增加。采用上述标准，图5（b）给出了II 区的水平范围与路基高度的关系曲线。可以看出，II 区的水平范围随路基高度的增加基本呈线性增加趋势，斜率约在7.5左右。

图5 坡前扰动区风速分布（a）及其水平范围与路基高度关系曲线（b）Fig.5 Wind speeds vs.height at different locations away from the windward slope foot of the embankment（a）and horizontal range of disturbed area at front of the windward slope foot vs.embankment thickness（b）

为掌握坡前扰动区（II）的高度范围，图6（a）给出了不同路基高度条件下坡脚处风速沿高度分布曲线。可以看出，路基高度越大，坡脚处风速较同一高度下环境风速越小，即路基的阻挡效应越明显。以1.5 m 高度为例，当路基高度为1 m 时坡脚处风速约为环境风速的93%，而当路基高度增加至5 m 时其坡脚处的风速仅为环境风速的53%左右。以环境风速的10%（0.35 m·s-1）为标准，即坡脚处风速与环境风速相差0.35 m·s-1为标准定义坡前扰动区高度范围。图6（b）给出了坡脚处坡前扰动区高度与路基高度之间的关系，可以看出这一高度范围与路基高度呈抛物线型增长趋势。当路基高度大于4 m 时，由式（7）可知，随高度的增加，风速曲线沿垂直高度的增量逐渐减小，导致坡前扰动区在坡脚处的高度范围随路基高度的增加不在显著增长。

图6 不同路基高度下迎风坡坡脚风速分布（a）与坡脚扰动区高度与路基高度关系曲线（b）Fig.6 Wind speed vs.height at the left slope foot with different embankment heights（a）and vertical range of disturbed area at front of the slope vs.embankment thickness（b）

2.1.3 路基上部加速区特征及范围

从图3 中可以看出，路基上部加速区（III）为高风速区，即受路基迎风坡的影响，当气流爬越路基时，在路基迎风侧受阻造成空气质量辐合，形成负高压（大于迎风坡前同一高度处正压），导致迎风坡侧路肩风速高于同一高度下的环境风速。图7（a）给出了3 m 路基高度条件下路面顶层不同位置处的风速沿高度分布曲线。可以看出，路面顶层同一高度条件下迎风坡侧路肩风速明显高于路面中部、背风坡路肩以及环境风速，这一差值随高度的增加先增大后减小。以3 m 高路基为例，迎风坡路肩与背风坡路肩最大风速差值可达1.37 m·s-1，约为同一高度下环境风速的39%。图7（b）给出了坡顶加速区路基上部最大风速差值与路基高度的关系，可以看出最大风速差值与路基高度基本呈线性增长趋势，斜率约为0.45左右。

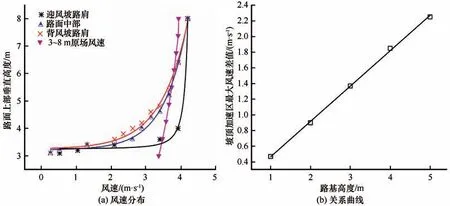
图7 路基上部加速区风速分布曲线（a）与迎、背风坡路肩最大风速差值与路基高度关系曲线（b）Fig.7 Wind speed vs.height above the embankment（a）and the maximum discrepancy between wind speeds at the windward and leeward shoulders vs.embankment thicknes（b）

2.1.4 坡后扰动区特征及范围

路基背风坡后扰动区（IV）为层流恢复区，即在重力作用下，受路基扰动导致的风速差异逐渐恢复到同一高度下的环境风速，动能逐渐降低，压力能逐渐增加。因此，为刻画IV 区的水平范围，图8（a）以路基高度3 m 为例给出了距离背风坡坡脚不同水平距离处风速沿高度的分布曲线。可以看出，背风坡坡脚处风速与同一高度下环境风速差值随高度的增加先增大后减小，在1.0～1.5 m 高度范围内两者差值接近1.5 m·s-1，约为环境风速的43%。随着距背风坡坡脚水平距离的增加，不同高度处风速逐渐增加并接近于环境风速。以两者的最大差值不超过环境风速的10%（0.35 m·s-1）为标准，则3 m 高路基条件下IV 区的水平范围约为30 m。随路基高度的增加，受迎风坡遮挡效应愈发明显，IV区的范围也相应增加。基于上述标准，图8（b）给出了IV 区的水平范围与路基高度的关系曲线。可以看出，IV 区的水平范围随路基高度的增加与II区的增加趋相同势皆为线性增加，斜率约在12.5左右。由静压云图可知，背风坡后静压值大于-0.2 Pa 后逐渐趋于稳定，其范围与图8（b）所示范围吻合。

图8 坡后扰动区风速分布（a）及坡后扰动区水平范围与路基高度关系曲线（b）Fig.8 Wind speeds vs.height at different locations away from the leeward slope foot of the embankment（a）and horizontal range of disturbed area behind the leeward slope foot vs.embankment thickness（b）

2.1.5 坡后涡动区特征及范围

当气流绕过路基到达背风坡侧时，坡后空气易于辐散，形成低压槽，最终发展为涡旋，且由图4（b）可知，越靠近路基背风坡处，负压值越大，导致越靠近路基背风坡处涡速越快，如图9所示。表1给出了在3 m高度处环境风速为3.5 m·s-1的条件下，不同路基高度与背风坡后最大涡速、涡旋最大横向范围之间的关系。可以看出，整个涡动区相较于同一高度环境风速明显较小，不同路基高度条件下涡动区内风速均小于1 m·s-1，约为同高度下环境风速的20%。涡动区内最大风速随路基高度的增加呈抛物线形增加，同样当路基高度超过4 m后其增加趋势不在明显。

图9 背风坡后涡旋示意图Fig.9 Vortex behind leeward slope of the embankment

表1 不同路基高度背风坡后涡旋横向最大范围Table 1 Maximum transverse vorticity at different roadbed heights

为刻画涡动区的横向最大范围，表1 给出了环境风速为3.5 m·s-1条件下，不同路基高度背风坡后横向最大范围与路基高度之间的关系。由表可知，随路基高度的增加，背风坡后涡旋横向最大尺寸逐渐增加。当路基高度为5 m 时，背风坡坡后涡动区横向范围超过20 m。随路基高度的增加，背风坡坡脚处的压力值逐渐减小，由动量守恒可知，动能逐渐提升，导致背风坡后涡旋的速度逐渐提升，且受路基高度的影响，背风坡后负高压水平范围（＜-1.0 Pa）明显增大，由1 m路基高度时的2.5 m增加到5 m 路基高度时的24 m，与背风坡后涡旋横向最大范围吻合。

2.2 分离式路基周边风流场特征

与单幅路基相比，分离式路基对周围风流场的扰动主要体现在两幅路基中间隔离带区域。图10（a）给出了在路基高度为3 m 时，两幅路基不同间距（不同隔离带宽度）条件下后幅路基迎风坡坡脚处风速沿高度的分布曲线。可以看出，当路基间距小于50 m 时，受前幅路基的阻挡，后幅路基坡脚处风速与同一高度下的前幅路基坡脚处的风速差值整体上随高度的增加先增大后减小。当隔离带宽度为20 m 时，后幅路基坡脚处4 m 高度范围内风速不足前幅路基坡前风速的1/3。随着隔离带宽度的增加，两者之间的差值逐渐减小。当隔离带宽度增加至60 m 后，后幅路基坡前风速与同一高度下的前幅路基坡脚处风速的整体差值小于10%（0.35 m·s-1）。即路基高度为3 m 时，两幅路基间距超过60 m 后，前幅路基对后幅路基坡前风速无显著影响。

图10 两幅路基迎风坡坡脚风速与高度间关系（a）及两幅路基之间坡前风速无相互影响的最小间距与路基高度关系曲线（b）Fig.10 Wind speed vs.height at the windward slope feet of the two separated embankments with different spaces（a）the minimum space between the two separated embankments without wind flow interaction vs.embankment thickness（b）

随路基高度的增加，前幅路基坡后扰动区与后幅路基坡前扰动区的范围都相应增加。为刻画出中间隔离带（H）受坡后扰动区跟坡前扰动区的混合影响，以后幅路基坡前风速与前幅路基的坡前风速差值不超过10%（0.35 m·s-1）为标准，图10（b）给出了在不同路基高度情况下，中间隔离带（H）的影响间距和路基高度之间的关系，可以看出这一影响间距与路基高度呈抛物线型增长。

通过与前幅路基坡后扰动区（IV）和后幅路基坡前扰动区（II）的范围之和作比较，可以看出在两幅路基的共同影响下，隔离带（H）的影响距离与后幅路基坡前扰动区（II）、前幅路基坡后扰动区（IV）和的差值随路基高度的增加而增加，由1 m 路基高度时的5 m 增加到5 m 路基高度时的40 m。由静压云图可知，两幅路基条件下，中间隔离带之间的负气压值（＜-0.2 Pa）范围随路基高度的增加呈抛物线型增加，导致两幅路基之间低风速区横向范围增加，后幅路基受前幅路基的影响范围逐渐上升。

3 结论

采用现场监测和数值模拟手段，对高海拔地区公路路基周边风流场进行特征区划研究并考察了路基高度的影响，结论如下：

（1）在风流自远场靠近路基、翻越路基并远离路基这一过程中，路基周边风流场可以划分为5 个区域，即进风场、坡前扰动区、路基上部加速区、坡后扰动区、出风场。对于对流调控类冷却路基以及路基周边风沙灾害而言，坡前扰动区、路基上部加速区、坡后扰动区内风流场特征值得关注。

（2）受路基阻挡效应作用，坡前扰动区为低风速区，沿高度方向坡前扰动区风速与环境风速差值先增加后减小，3 m 路基高度条件下迎风坡坡脚0.5～2.0 m 高度范围内风速约为环境风速的30%。以环境风速与坡前扰动区不同高度最大风速差异不超过环境风速的10%为标准，3 m 路基高度条件下坡前扰动区水平范围约为15 m。这一水平范围随路基高度的增加呈线性增加趋势。

（3）受迎峰坡坡面气流爬升辐合效应影响，路基上部为高风速区，尤其迎峰坡路肩处为高压脊其风速明显大于环境风速、路面中部及背风坡风速。当路基高度为3 m 时，迎峰坡路基与背风坡路基最大风速差值为1.4 m·s-1，约为同一高度下环境风速的39%。且最大风速差值与路基高度基本呈线性增长。

（4）气流翻越路基后为坡后扰动区，为低风速区。以扰动区内风速与同一高度下环境风速差值不超过环境风速的10%为标准，3 m 高路基条件下坡后扰动区水平范围约为30 m。随路基高度的增加，坡后扰动区水平范围呈线性增加。在坡后扰动区靠近背风坡坡脚区域，受气流辐散效应影响，背风坡坡后形成涡旋区，整体风速仅为环境风速的30%。涡旋区水平范围与路基高度相关，随路基高度增加涡旋区水平范围基本呈线性增加趋势，5 m高路基条件下涡旋区水平范围可超过20 m。

（5）分离式路基中受前幅路基的影响导致后幅路基坡前风速下降明显。以后幅路基坡前风速与前幅路基的坡前风速差值不超过10%（0.35 m·s-1）为标准，3 m 高路基条件下两幅路基最小间距为60 m。随路基高度的增加，这一最小间距呈抛物线型增加。因此，为保证冻土区分离式对流换热类冷却路基的冷却降温效果，两幅路基间的间距应不低于60 m。