Unpinning the spiral waves by using parameter waves*

Lu Peng(彭璐) and Jun Tang(唐军)

School of Materials and Physics,China University of Mining and Technology,Xuzhou 221116,China

Keywords: pinned spiral wave,heterogeneity,pinning force

1. Introduction

Self-sustained pattern formation in spatial extended excitable systems has attracted much attention in research of nonlinear dynamics. It has been found that two-dimensional(2D) pattern formation, including spiral wave, could be sustained in the small world excitable network, and the patterns are robust against perturbations.[1,2]Qian et al. searched for optimal oscillation pattern in the spatial extended excitable network by modulating network topology.[3,4]Rotating spiral wave is one kind of characteristic patterns in different spatial extended excitable mediums. For example,intracellular Ca2+spiral waves have been observed in Xenopus oocytes.[5–9]The spiral wave in the Belousov–Zhabotinskii reaction has long been a research hotspot in nonlinear dynamics.[10–14]Spiral waves of electrical activity in cardiac tissues have been associated with life-threatening arrhythmias because of the breakdown of the normal rhythmic pumping action in hearts.[15–20]The clinical observation indicates that the transition from ventricular tachycardia(VT)to ventricular fibrillation(VF)corresponds to spiral wave breakup,in which an initiated single spiral wave breaks up after several rotations into multiple spiral waves.[21–23]Thus, controlling and removing the spiral wave is a problem of fundamental interest.

In the homogeneous medium,the spiral wave can be controlled by a wave train released from a local source. The persistent wave train may push the spiral to drift. The spiral tip is eventually driven to the boundary and thereby eliminated from the system. However,the problem will be more complicated when the system is inhomogeneous. Inhomogeneity can initiate,[6,8]break up,[24,25]or suppress[17,25]spiral waves in different circumstances. The effect of inhomogeneity on the movement of the spiral tip has drawn much attention.[26–31]It has been widely reported that the spiral tip will get pinned to large size of heterogeneity. Our former work reports that heterogeneity repels the approaching spiral tip, while attracts the anchored spiral tip. Quantitative results indicate that the attractive force is much larger than the repulsive one.[32]This implies that it is more difficult to eliminate the pinned spiral wave than the freely rotating one.

Theoretically,the advection field is usually used to resist the pinning force and unpin the tip for the heterogeneity. In heart muscles,electric pulses delivered at the boundary of the heterogeneity are able to remove the pinned spiral waves.[30]As a mechanosensitive medium, mechanical deformation of heart tissues also dedicates the pinning and unpinning of spiral tip.[31]

In our previous work, the parametric wave is introduced to control spiral waves in a homogeneous medium.[33]The parametric wave means that the parameter, which determines the excitability of medium, changes like a propagating wave.The results show that the parametric wave could push the spiral tip out of the medium,thereby eliminating the spiral wave.In this paper, we attempt to unpin the anchored spiral wave using the parametric wave. The factors that influence the capability of parametric wave in unpinning spiral tip are studied systematically.

2. Model and simulation

Following the literature, the Barkley equations are employed to model the excitable medium,[32–34]

where u is the activator variable while v is the inhibitor one.The constant ε is the ratio of characteristic time scales of the two variables, which determines the excitability of the medium. The parameters a and b represent the slope of the u nullcline and the excitation threshold, which determine the local dynamics of the system.In this study,we fix the diffusive constant D at 0.5,and b=0.05.

In this paper,we model a 2D 50×50 excitable medium.In the numerical simulations,no-flux boundary condition is used.The equations are integrated using an Euler forward scheme,with a spatial discretization of 0.125 and a time step of 0.005.Simulations verify that further time step reduction does not significantly improve accuracy. It is reported that the system sustains a rigidly rotating spiral wave when a ＞0.76.[34]For simplicity, we will initiate spiral wave in the homogeneous system with a=a0=0.8. First, the spiral wave with one tip is developed from an unphysiological initial condition. The initial condition is that,in a square area,u decreases from left to right while v increases, and in positions out of the square area,all u and v are set at rest state. Then,to anchor the spiral tip, a circular region with radius Riare selected as the inhomogeneous area,which is located at the center of the system.The heterogeneity is implemented by varying the value of parameter a in the inhomogeneous area. The value of a in the inhomogeneous area is set as ai,and the ratio ai/a0quantifies the level of the parametric heterogeneity.

To unpin the spiral tip from the inhomogeneous area,the parametric wave is added. The parametric wave is implemented by letting the value of a change to yield wave propagation. For simplicity,we consider a plane harmonic parametric wave propagating along the x-axis.[33]The wave equation is given by

where A is the amplitude of the parametric wave, f is the frequency, and λ is the wavelength. Here, λ equals the wavelength of spiral wave in the homogeneous system, and f will be modulated in the unit of frequency of the spiral wave fs.

3. Results and discussion

An inhomogeneous area with higher excitability can emit pulse or wave front,thus it could be treated as a wave source.On the other hand, the unexcitable heterogeneity in an excitable medium can break up the travelling waves and produces spiral waves with several attached tips. For simplicity,the value of aiwill be selected to guarantee that the two extreme circumstances will not occur. The pinned spiral wave is more difficult to be eliminated than the freely rotating one.[26]Thus, the parametric wave with larger amplitude is used to eliminate the pinned spiral wave. As shown in Fig. 1, the anchored spiral wave is unpinned successfully from the heterogeneity by parametric wave with amplitude A=0.08. The spiral tip is separated from the heterogeneity after the parametric wave is added for about 91.0 time units. The tip trajectory indicates that,once the tip is separated,it will be pushed to the boundary quickly in several rotating periods. Compared the amplitude with that of parametric wave used to control spiral wave in the homogeneous medium(see Fig.1 of Ref.[33]),it is confirmed that the pinned spiral wave is more difficult to be eliminated than the freely rotating one.

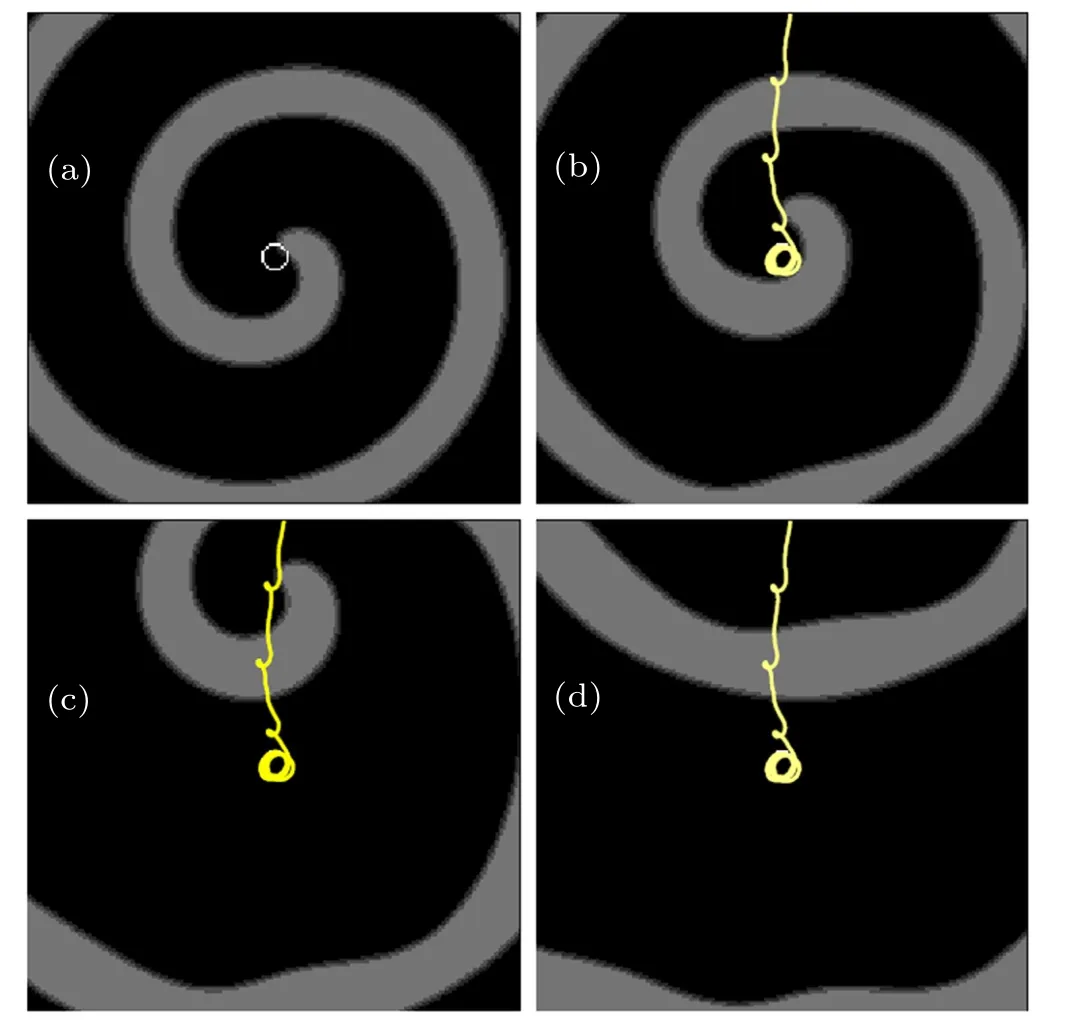
Fig. 1. Snapshots illustrating the unpinning of spiral tip from the heterogeneity aided by parametric wave. The white circle represents the heterogeneity,and the yellow curve exhibits the trajectory of the spiral tip. (a) The spiral wave pinned on the heterogeneity with Ri =0.725 space unit. (b)–(d) The spiral patterns after the parametric wave are added for about:(b)95.0 time units,(c)105.0 time units,(d)125.0 time units. The amplitude of the parametric wave is 0.08, the frequency is 0.7fs, and the value of parameter a in the heterogeneity ai =0.55. To show the heterogeneity and tip trajectories explicitly, only 1/4 of the medium is depicted.

Numerical simulations show that parametric wave with amplitude larger than a critical value Aiis always capable of unpinning the spiral tip. Advection field exerts force on the spiral waves to resist the attraction of heterogeneity, thus, induces the separation of spiral tip. The critical intensity of the field is used to quantify the pinning force. Parametric wave plays the similar role in unpinning spiral wave as advection field does. Unlike advection field, the amplitude is not the only one parameter determining the parametric wave. Thus,the critical value of amplitude could not be used to quantify the pinning force directly as the critical intensity of advection field does.It is well known that the pinning force increases with the size of heterogeneity monotonously.[26,32]Figure 2 shows that the critical amplitude almost always increases with the size of heterogeneity for given frequencies. When the frequency of parametric wave is fixed,the critical amplitude could be used to quantify the pinning force. Here,the parametric wave could be treated as a nonlinear spatiotemporal force exerted on the spiral wave. Higher amplitude corresponding to higher intensity of average force is used to resist pining force.

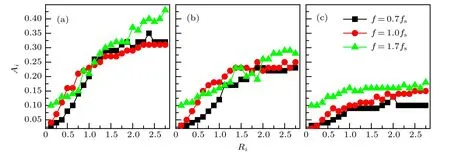
Fig.2. The critical value of amplitude Ai,above which the spiral wave could be unpinned by parametric wave,as a function of heterogeneity size: (a)ai=0.45,(b)ai=0.55,(c)ai=0.65.

Fig.3. Snapshots illustrating the effect of frequency of parametric wave on the unpinning of spiral tip. The frequency of parametric wave: (a)f =0.7 fs, (b) f =1.0 fs, (c) f =1.7fs. Other parameters are A=0.11, ai =0.55 and Ri =0.725. The snapshot in (b) is selected after the parametric wave is added for sufficient time(700 time units). To show the heterogeneity explicitly,only 1/4 of the medium is depicted.

Fig.4. The critical value of amplitude Ai,above which the spiral wave could be unpinned by parametric wave,as a function of frequency. (a)Ri=0.375,(b)Ri=0.725,(c)Ri=1.250.

In the homogeneous medium, the frequency of parametric wave determines the drifting velocity and direction as well as the amplitude.[33]Thus, the effect of the frequency on the unpinning of spiral wave will also be checked systematically.As shown in Fig. 3, the spiral waves are unpinned successively when f =0.7fsand 1.7 fs,while they fail to unpin when f =1.0fs. The examples in Fig.3 indicate non-monotonic dependence of unpinning on the frequency.

Suppose the pinning force is constant for given values of parameters. The minimum force, provided by parametric wave to resist the pinning force, is also constant. As mentioned above,the frequency may change the capability of providing resistant force. Based on extensively simulations, the critical amplitude Aifor unpinning is depicted as a function of frequency f. The dependence of Aion f is complicated and oscillate-like. Roughly speaking,there are two valleys on the curves of f to be around 0.7 fsand 1.7 fsfor almost all values of other parameters. The two valleys indicate that minimum amplitude of parametric wave is needed for unpinning when f ≈0.7fs,or 1.7fs. This implies that 0.7 fsand 1.7 fsare optimal values of frequency.

In the Barkley model,the parameter a determines the local dynamics of the medium significantly.[34]Only a ＞0.76 allows the rigidly rotating spiral waves. Once a decreases to a value below 0.45, the medium could not support any spiral wave because the medium becomes unexcitable. The ratio ai/a0is defined as the degree or level of heterogeneity. Obviously,smaller ai/a0corresponds to higher level of heterogeneity, the system is totally homogeneous when ai/a0=1. We have also checked the effect of the heterogeneity level on the unpinning. In Fig.5,we can see that the critical amplitude always decreases with the ratio ai/a0,though some plains could be found in the curves explicitly. This indicates that higher level of heterogeneity provides more stronger pinning force.When the ratio ai/a0approaches 1,i.e.,the medium becomes homogeneous,the critical amplitude decreases to a value less than 0.01. This is consistent with the results in the homogenous medium.

Once the spiral tip is unpinned from the heterogeneity,the tip drifts to the boundary along straight line. Figure 6 shows that the amplitude and frequency could both modulate the drifting direction. Obviously,the modulation range of the frequency may surpass the angle of 180°,which is much larger than that of the amplitude. Furthermore,the drift trajectory is similar to that found in the homogeneous medium.The heterogeneity is only able to act on the spiral tip which is adjacent to itself.[35]Thus, when the spiral tip is unattached from the heterogeneity,and drift to boundary,the drift direction can be determined by the homogeneous medium.

Fig.5.The critical value of amplitude Ai,above which the spiral wave could be unpinned by parametric wave,as a function of the heterogeneity level. (a)Ri=1.250,(b)Ri=0.725,(c)Ri=0.375.

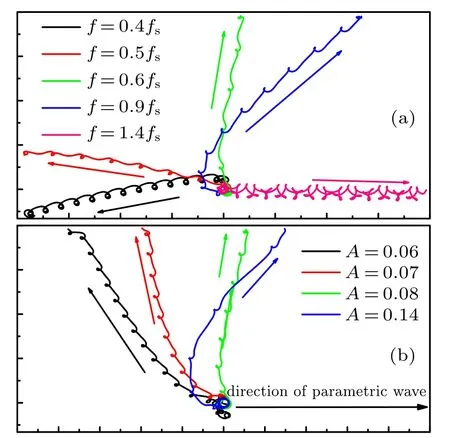
Fig.6. Tip trajectories illustrating the modulation of drift direction by amplitude and frequency of parametric wave. (a)Ri =0.375, A=0.1;(b)Ri=0.375, f =0.7 fs. The parameter value ai=0.55.

4. Conclusion

In summary,we have employed the Barkley model to simulate the 2D excitable medium,[34]and the spiral wave,which is pinned on an circular heterogeneous area in the center of the medium, is developed from an unphysiological initial condition. The plane harmonic parametric wave is used to control and eliminate the pinned spiral wave. It is found the parametric wave with large enough amplitude and proper frequency is capable of unpinning the spiral wave. It can be concluded that the parametric wave could provide “resistant force” to resist the pinning force. And the factors influence the resistant force are studied systematically. At first,only parametric wave with enough large amplitude could unpin the spiral wave.Secondly,the dependence of the resistant force on frequency is complicated and oscillate-like,and f ≈0.7fs,or 1.7fsare the optimal frequency for unpinning spiral tip. Then,using the parametric wave, it is further confirmed that the pinning force increases with the size of heterogeneity,and decreases with the level of inhomogeneity. Finally,the amplitude and frequency of parametric wave could both modulate the drifting direction, and the modulation range of the frequency is much larger than that of the amplitude.