Energy behavior of Boris algorithm

Abdullah Zafar and Majid Khan

1Department of Engineering and Applied Physics,University of Science and Technology of China,Hefei 230026,China

2Department of Physics,Quaid-i-Azam University,Islamabad 45320,Pakistan

Keywords: Boris algorithm,invariant tori,chaotic system,H´enon-Heiles potential

1. Introduction

Motion of a non-relativistic particle of charge q and mass m in the electromagnetic fields is governed by Newton’s law by taking into account the Lorentz force,i.e.,by the following set of equations:

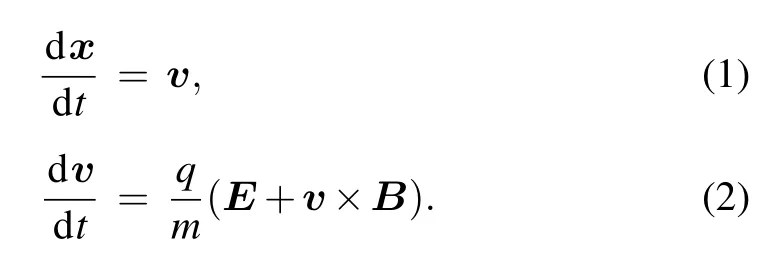
The discretized form of the above equations for the Boris algorithm can be written as[1–3]

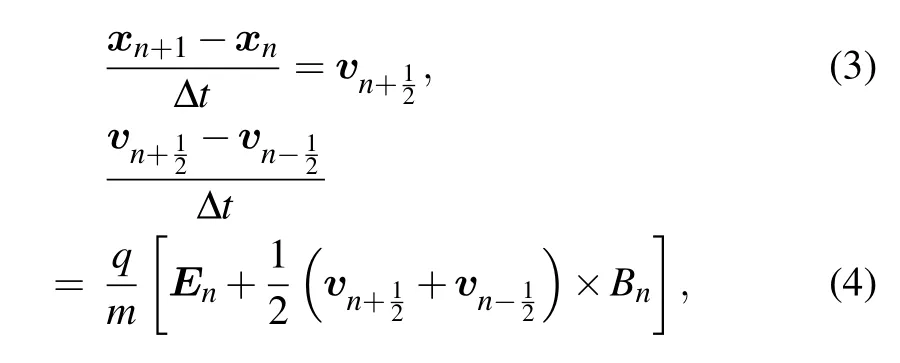
where En=E(xn), and Bn=B(xn) are time-independent electric and magnetic field vectors. Despite its simplicity,the Boris algorithm has many advantageous features: it exhibits a long-term accuracy compared to its counterpart,such as the fourth order Runge–Kutta (RK4) method. Moreover, it has been observed that the global error of energy and other conserved quantities,e.g.,canonical momentum,can be bounded for all time steps in the Boris scheme, not to mention the exact energy conservation in the absence of an electric field.[3]Due to these excellent properties, Boris algorithm has been widely used in simulation studies of magnetized plasmas.[3–5]A common misconception about the underlying cause of the long-term fidelity is that the Boris algorithm is a symplectic integrator.[6–8]However,it is actually a volume-preserving method. Further,an earlier study has highlighted that no variational formulation of the Boris algorithm exists, indicating that the long-time stability should be attributed to its volumepreserving characteristics.[9–11]Unlike the symplectic integrator,whose long time energy conservation has been rigorously demonstrated by a backward error analysis,[12]the volumepreserving integrator has a little to do with this energy conservation. We refer readers to Refs.[2,13]where one can counter an example for which Boris algorithm cannot keep a long time energy conservation and the special conditions under which it can bound these errors. Near-conservation of energy, over long simulation times, has been demonstrated under the conditions that the magnetic field is constant or the electric potential is quadratic in nature.[2]Nonetheless,the energy behavior of the Boris algorithm in the general cases is not very well understood. This motivates our study to reveal the underlying causes of the different energy behaviors associated with the Boris numerical scheme. The research interests of structure preserving integrators were originated from its qualitative numerical superiority, e.g., conservation of the Kolmogorov–Arnold–Moser (KAM) tori. The near invariant tori of symplectic integrators leads to energy conservation. Similarly,some earlier studies have shown that the invariant torus exists in volume-preserving maps.[14,15]To be specific, under certain non-degeneracy conditions,any n-dimensional smooth volume-preserving maps close to the integrable ones,preserve a large set of invariant (n −1)-dimensional tori.[16]Thus, if the Boris algorithm can preserve the tori, then the conservation of energy would be obtained as a result. Here, we have shown the long-time energy behavior of Boris method for a 2-degree-of-freedom autonomous Hamiltonian. Numerical experimentation reveals that such an algorithm exhibits several kinds of energy errors. When the invariant tori can be preserved under Boris discretization,the energy error is bounded for an exponentially long time. However, if the invariant tori are not preserved, the error exhibit a linear growth. On the other hand, when the Hamiltonian system is non-integrable,Boris algorithm does not conserve energy and exhibits a random walk behavior on the global energy error. For all numerical examples, the symplectic integrator is implemented as a control group for comparisons, which shows a long time energy conservation regardless of whether the original system is integrable or otherwise.

The rest of the article is organized as follows: mathematical description of the model is presented in Section 2. Key results are discussed in Section 3. Finally,a brief summary of the main results is presented in Section 4.

2. Mathematical description of the model

The specific scheme of Boris algorithm used here is a second-order symmetric version, described by the following set of discretized equations

where all the terms have their usual meaning. We have performed our numerical experiments based on the H´enon–Heiles Hamiltonian system,[18]for investigating the invariant tori.The canonical H´enon–Heiles Hamiltonian describes the motion of stars around a galactic center,assuming that the motion is restricted to the x–y plane. The corresponding potential can be expressed as[18]

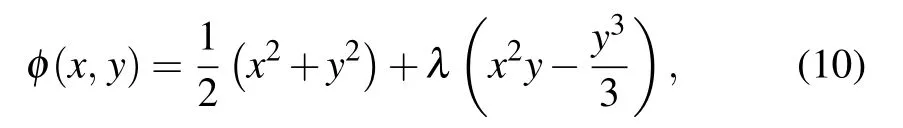
where λ is a constant, x and y are coordinates. The motion under this potential can be seen as double harmonic oscillators coupled with the term associated with λ. It has been seen that the third integral exists only for a limited number of initial conditions.[18]In the modern perspective, the initial conditions that do not exhibit a third integral of motion is correlated with chaotic orbits. To implement the Boris method to a more general case, an extra non-constant magnetic field has also been added. For a constant magnetic field, the onestep map of the Boris algorithm (xn,Pn)→(xn+1,Pn+1) is symplectic,where Pn=Vn+eAn. This follows from the fact that the Boris method is a variational integrator if and only if B is a constant.[9]Thus, to investigate the energy behavior of the Boris scheme from its volume-preserving property, without loss of generality,we choose the asymmetric and variable magnetic field as given by

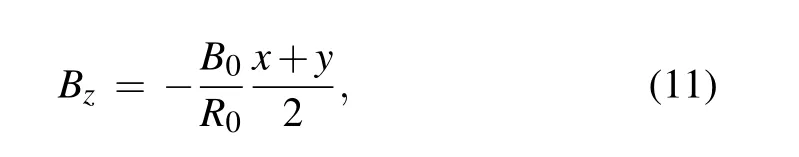
with the corresponding vector potential written as

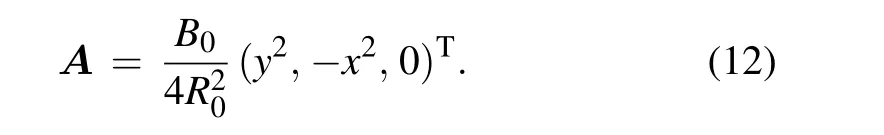
On the basis of this system, we can generate various orbits as affected by different initial conditions, which can correspond to integrable and non-integrable regimes. Also, different λ parameters have been used for the construction of the desired Hamiltonian,e.g.,λ =1 is a regime in which the integrability depends on the initial conditions,while λ =0 corresponds to an integrable systems.

Firstly, the phase space behavior of the H´enon–Heiles system has been studied by plotting the Poincar´e maps,which is a recurrence plot and can be applied to distinguish chaotic,periodic, or quasi-periodic motions. It focuses only on that regime where the orbit intersects the bottom part of the Poincar´e section, instead of studying the motion in the entire phase space. If there are only a few intersection points,then the motion is periodic. If the intersection points constitute a line,the motion is quasi-periodic and if such points are dense and form a random structure,it corresponds to a chaotic regime.[19]In practice,we fix one phase element and plot the other elements each time the selected element has the desired value,thus an intersection surface is obtained. For the H´enon–Heiles Hamiltonian, these plots exhibit various phase space orbits correspond to chaotic and regular motions,with respect to different initial conditions. It is important to note that, in this work,we will use normalized(dimensionless)quantities.

Figure 1 shows the Poincar´e maps of the H´enon–Heiles system,and highlights that this system strongly depending on initial conditions can be either integrable or non-integrable.The breaking of the invariant tori can be observed for increasing values of the initial energy,e.g.,for E0=0.16,the system also exhibits chaotic behavior.

Fig. 1. Poincar´e plots of H´enon–Heiles Hamiltonian in (y,Py) plan, with initial energy of(a)0.1 and(b)0.16.

Secondly, the orbit in configuration space can be classified by the means of Fourier transformation,which gives an alternative way to identify the invariant tori.[20–22]For a canonical integrable Hamiltonian system with n degrees of freedom,we can find a canonical transformation,from(p,q)to(I,ϕ),i.e.,

where i=1,2,...,n. The transformed coordinates (I,ϕ) are called the action-angle variables, which, for a special case H=H(I),correspond to the Hamilton’s equations

The motion on a specific torus has a fundamental frequency and thus a total of n, such values for an integrable system,namely ν1,ν2,...,νn. Further,the canonical coordinates(q,p)can be expressed as the function of the periodic parameter ϕ as the Fourier representation,i.e.,

where ν is a fundamental frequency vector, and n is an nvector with integer components in the interval[−∞,+∞]. The Fourier coefficients qnare functions of the action I.[21]

The chaotic and regular orbits corresponding to different initial conditions are shown in Fig. 2, and the discrete fourier transform (DFT) of these orbits is depicted in Fig. 3.As discussed, the spectrum for the integrable system is discrete,whereas for the chaotic motion it exhibits a white noise pattern.

Fig. 2. A regular and chaotic orbit of the H´enon–Heiles system. The initial condition for the regular orbit is (a) X =[0,0.1,0]T, V = [0.157073238266067,0.269255830975273,0]T,while for the chaotic orbit we have (b) X =[0,0.1,0]T and V =[0.282596864122024,0.490039806942659,0]T.

Fig. 3. The DFT spectrum characteristics of orbits for regular and chaotic patterns. The initial conditions are the same as in Fig.2.

3. Numerical analysis and discussion

Using the above mentioned scheme,we have investigated the energy error evolution of a single as well as group of statistical charged particles. Moreover, the classification of the orbital type and the correlation of the energy behavior of the Boris algorithm with the system integrability has also been presented. For the demonstration of orbits and energy behavior,we have used the symplectic integrator as a benchmark.

3.1. Energy behavior under different Hamiltonian regimes

First we set λ =0 and plot the consequent phase section in Fig.4,which exhibit a regular path and the Boris algorithm depicts an excellent long time energy conservation. As for the case of λ =0, the harmonic oscillators are decoupled, therefore the KAM structure is not associated with the corresponding initial energy.As a consequence,the Poincar´e section consists of several concentric closed orbits and is not perturbed by increasing initial energy.

Fig.4.Poincar´e plot of H´enon–Heiles Hamiltonian with the additional asymmetric magnetic field, within the potential parameter λ =0. The initial energy is 0.1.

Fig.5.The orbits of a particle calculated by Boris and symplectic integrators.The initial condition is X =[0,0.82,0]T, V =[0.123201731589563,0,0]T and the corresponding initial energy is E0=0.16,dt=0.001 and λ =0.

For a given initial conditions X = [0,0.82,0]T, V =[0.123201731589563,0,0]Tand E0=0.16, the phase space orbits evaluated by Boris and symplectic algorithms have been illustrated in Fig. 5. In this case, the particle moves along an elliptical orbit while pressing around the counter-diagonal.The motion is quite regular,having several fixed frequencies.

The relative energy errors of Boris and symplectic schemes have also been studied for a long simulation time(about one million iterations)and the findings are depicted in Fig.6. In this case,both Boris and the symplectic integrators have kept the energy error bounded.

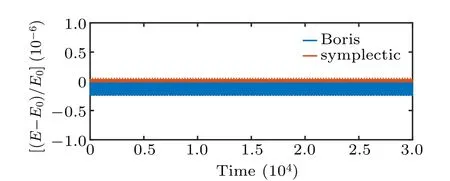
Fig. 6. The evolution of relative error of energy for Boris and symplectic numerical schemes. Initial condition is X = [0,0.82,0]T, V =[0.123201731589563,0,0]T,time interval is dt=0.001,and we iterate over 3×107 steps to show the long time behavior of energy error.

Fig. 7. Poincar´e plot of H´enon–Heiles Hamiltonian system with the asymmetric magnetic field. The Poincar´e section of the surface lies on the(y,Py)plane as well,the initial energy in(a)is 0.1,and in(b)is 0.16.

The second example presents a non-integrable Hamiltonian system,i.e.,we set λ =1,and the computed phase space structure under different initial energies are shown in Fig. 7.After the asymmetric magnetic field is appended, the phase space structure is distorted and becomes complicated. Compared to Fig. 1, for the same energy level E0=0.1, more islands among regular concentric circles appears, moreover at even high values,e.g.,E0=0.16,the entire phase section becomes irregular.

Without losing any generality, we could investigate the energy behavior of Boris algorithm for H´enon–Heiles Hamiltonian. In this regard, comparisons of the chaotic orbit and corresponding relative energy errors of Boris and symplectic algorithms are shown,respectively,in Figs.8 and 9. The initial conditions used here are the same as those in Fig.7. The energy error of these chaotic orbits reveals a random walk behavior in particular this error for the Boris stochastically increases with iteration time while symplectic integrator depicts a long term conservation of energy.

Fig. 8. The orbit in configuration space calculated by Boris algorithm and symplectic integrator. The initial condition is X =[0,0.82,0]T, V =[0.123201731589563,0,0]T,time interval is dT =0.001,and we iterate for 3×105 steps. The blue line denotes the result of the Boris algorithm and the black line denotes the result of the symplectic integrator. The red dot is the initial position. Under this condition,the orbit exhibits a chaotic pattern.

Fig. 9. The evolution of relative error of energy for Boris algorithm and symplectic integrator. The initial condition is X =[0,0.82,0]T, V =[0.123201731589563,0,0]T,time interval is dT =0.001,and we iterate for 3×107 steps.

To investigate the energy behaviors of Boris algorithm statistically, we consider a group containing 10 particles, all with E0= 0.16 and randomly distributed in velocity space.The evolution of the energy error for the entire particle group is shown in Fig. 10. Here one can observe two distinct error responses, namely a “random walk” pattern and “long time conservation”pattern.

Next,we show an example of having the“irregular”orbits and a linear energy error. For that consider the initial energy E0=0.1,which corresponds to a regular orbit in the original H´enon–Heiles system. However, with the asymmetric magnetic field, the shape of the orbit turns out to be irregular but not chaotic(the orbit is not sensitive to the initial value). The irregular orbits and their resulting energy behavior of Boris and symplectic integrators are illustrated in Figs. 11 and 12,respectively. In this case, the energy error of the Boris algorithm exhibits a linear growth pattern,while the energy of the symplectic simulations remains well conserved.

Fig. 10. Energy behavior for a group of 10 particles with the initial energy E0=0.16,initial position X =[0,0,0]T,and randomly chosen the sampling points in velocity space. The time interval is dt =0.001 and the calculation steps are 3×107 steps for each sampling particle.The black line is the results of the symplectic algorithm. The colored lines denote the results from Boris algorithm.

Fig. 11. An irregular orbit calculated by Boris and symplectic integrators. The initial condition is X = [0,0,0]T, V =[−0.373621484848066,0.245778327075286,0]T, dt = 0.001 and 3×105 steps. The two orbits completely overlap,which means that orbit is not chaotic.

Fig. 12. The evolution of relative energy error for initial condition X =[0,0,0]T, V =[−0.373621484848066,0.245778327075286,0]T, time interval is dT =0.001, and the simulations is performed over 3×107 steps to show the long time behavior.

3.2. Analysis of error growth pattern

In the preceding sections,we have discussed three typical energy trends associated with the Boris scheme. In this regard,the corresponding orbits and the Poincar´e sections show a correlation between energy and system integrability.The energy error of the Boris algorithm shows a random walk pattern for particles exhibiting a chaotic motion. However,the causes for the linear-growth in energy error are not well understood.Here some typical cases with such trends have been analyzed,and the results are compared with the corresponding integrable cases. In the following, we will present a brief discussion on the phase sections and the spectrum characteristics of those motions.

We choose an initial point,which corresponds to the regular structure in the Poincar´e maps,e.g.,as shown in Fig.7(a).Although this initial condition corresponds to a quasi-periodic motion in which there exists an invariant tori, the Boris algorithm still results in linear growth. The Poincar´e plot of a specific particle is shown in Fig.13.

Fig.13. The Poincar´e maps for a particle exhibiting a periodic orbit. The initial energy for this particle is 0.1, and the initial condition is X =[0,0,0]T,V =[−0.373621484848066,0.245778327075286,0]T.

From Figs.11 and 13,we can see that the motion is quite regular and quasi-periodic,which means that the invariant tori is existed and Boris algorithm would be able to conserve the energy error for this condition. However, it shows a linear growth pattern as depicted in Fig. 12. Actually, the error growth of Boris has originated from the breaking of invariant tori during iterations. To demonstrate this,we apply the DFT to show the information about the invariant tori.

As discussed in Eqs. (13)–(17), the x component of the orbits data is a finite time sequence as functions of actionangle variables. Thus,a discrete Fourier transformation shows the amplitudes and the frequencies information of the invariant tori. By comparing the spectrum of different orbits, obtained through Boris and symplectic methods, we can quantitatively analyze the evolution of invariant tori,i.e.,the energy behavior with respect to KAM structure can be revealed.

To investigate the invariance of tori, the difference of spectrum of orbit sequences for Boris and symplectic schemes are calculated and the results are presented in Fig. 14. The amplitude as evaluated by Boris method is 3 to 4 orders larger than its symplectic counterpart. Thus,for such systems,Boris can not preserve the structure of invariant tori,and for this reason, it exhibits a linear growth in the energy. To further clarify, a complete integrable system has been investigated, with the same initial conditions as in Fig. 5. The Boris algorithm shows a long time energy conservation,and the spectrum difference of the orbit in this case is presented in Fig. 15. We can observe that the amplitude difference is around 1–2 orders smaller than its corresponding case (see Fig. 14). Thus, the invariant tori are preserved under Boris discretization, consequently,the energy error is well behaved.

Fig.14.The difference of spectrum for the two slices of orbit sequences.The blue line denotes the results of Boris while the black line represents symplectic results.

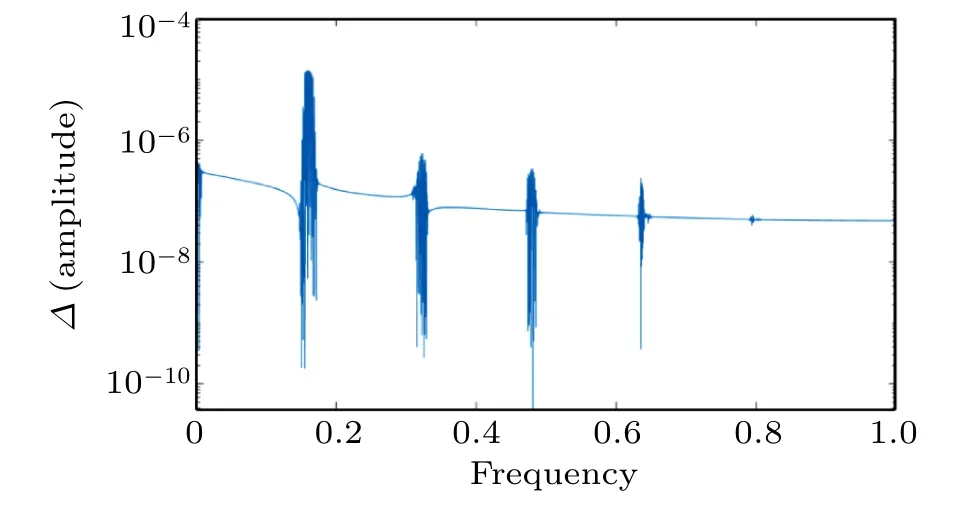
Fig.15. The characteristic spectrum difference of orbit sequences with simulation time. In this case, The parameter λ in scalar potential is set to be 0.

4. Summary

To conclude,we have shown various kinds of energy error behaviors of the Boris algorithm for the motion of a charged particle in an electromagnetic field. The energy errors in our numerical examples strongly depend on the integrability of the Hamiltonian. If the Hamiltonian of our system is chaotic,i.e.,no invariant tori exists in this case, the energy error of Boris algorithm has a random walk pattern. However,if there is an invariant tori in the original Hamiltonian system,but is not preserved under Boris discretization,the error will exhibit a linear growth. As a comparison, the global bound on energy error typically associated with symplectic algorithms still holds for all numerical examples.

Acknowledgements

Abdullah Zafar acknowledges the Chinese Scholarship Council(CSC)to support him as the 2015 CSC awardee(CSC No. 2015GXZQ56). The authors would like to thank Dr.Jiangshan Zheng for the technical discussion.