Numerical simulation on partial coalescence of a droplet with different impact velocities*

Can Peng(彭灿), Xianghua Xu(徐向华), and Xingang Liang(梁新刚)

Key Laboratory for Thermal Science and Power Engineering of Ministry of Education,School of Aerospace Engineering,Tsinghua University,Beijing 100084,China

Keywords: droplet impact,partial coalescence,volume of fluid(VOF)method

1. Introduction

Droplet impact is a ubiquitous phenomenon that will be encountered in a wide range of engineering fields such as ink-jet printing,[1]fuel injection in engines,[2]spray coating,[3]and spray cooling.[4–6]Previous studies revealed that different impact conditions would result in different behaviors: splashing,[7–9]full coalescence,[10,11]and partial coalescence.[11,12]Partial coalescence is a peculiar impact result during which the droplet does not coalesce with the underlying liquid completely and a daughter droplet will be pinched off.[11]For the practical significance and complexity, partial coalescence attracts plenty of researchers’interests.

Partial coalescence only emerges under certain circumstances. Charles and Mason[11]proposed a criterion of 0.02 ＜µ*＜7–11, where µ*is the viscosity ratio. Chen et al.[13]found that there was a special droplet size range for partial coalescence. Analysis from Blanchette and Bigioni[14]indicated that there was a critical Ohnesorge number for partial coalescence and the critical Ohnesorge number was approximately 0.026 at a low Bond number. And the critical Ohnesorge number was affected by the density ratio and viscosity ratio. Aryafar and Kavehpour[15]observed that there was no daughter droplet pinched off when the Ohnesorge number was larger than 1. Yue et al.[16]divided the critical Ohnesorge number Ohcinto three zones in terms of the viscosity ratioµ*and the density ratio ρ*. For µ*＞0.4,Ohcwas nearly constant with a value close to 2.45×10−2. For ρ*＞0.5 andµ*＜0.4,Ohcdepended mainly onµ*. For ρ*＜0.5 andµ*＜0.4,the contours of Ohcshowed a ridge-like structure.

To gain a better insight into partial coalescence,the mechanism was discussed by several researchers. Charles and Mason[11]attributed partial coalescence to the Rayleigh instability. Blanchette and Bigioni[14]argued that it was the capillary wave convergence rather than the Rayleigh instability that led to partial coalescence.They noticed that the capillary wave could distort the droplet and stretch it upward, which helped the horizontal collapse exceed the vertical collapse. Ray et al.[20]believed that it was the competition between horizontal and vertical momentum that determined the transition between partial coalescence and full coalescence. When the horizontal momentum exceeded the vertical momentum, partial coalescence took place. Mohamed-Kassim and Longmire[21]evidenced the generation of the capillary wave with PIV experiments. Chen et al.[13]also observed the capillary wave, and they found that the uplifting effect of capillary waves thinned the liquid column in the first stage of partial coalescence and the capillary instability led to the pinch-off in the second stage.Gilet et al.[19]investigated the capillary wave propagation and damping. They concluded that the convergence of capillary waves was not the only mechanism and other viscous mechanisms were also involved. Yue et al.[16]thought that there was an energy barrier due to the increase of interface. If the kinetic energy was large enough to overcome the energy barrier partial coalescence would take place. Otherwise,the full coalescence happened. Although many researchers have put forward valuable analyses and explanations,some unclarity still remains on the partial coalescence mechanism. The capillary wave is just one aspect of the mechanism.

In the present study,the coalescence process is simulated with the volume of fluid(VOF)method. Firstly,the effects of the droplet impact velocity on the daughter droplet diameter ratio and coalescence time are investigated. Secondly,the importance of a downward high-velocity region for the droplet evolving into a prolate shape and the final pinch-off is discussed. And the shift from partial coalescence to full coalescence is explained based on the droplet shape before the pinch-off. Thirdly,the influence of film thickness on the coalescence is investigated. Finally,the effects of surface tension coefficient,viscosity and initial droplet diameter on the critical droplet impact velocity are studied.

2. Computational model

2.1. Simulation system

The droplet is set as a sphere above the underlying liquid at the initial moment. Both the droplet and underlying liquid are water. The ambient fluid is air. The physical properties are assumed to be constant. Since the flow during the coalescence is rotationally symmetric, the 2D axisymmetric model is applied. The boundary conditions are shown in Fig.1.

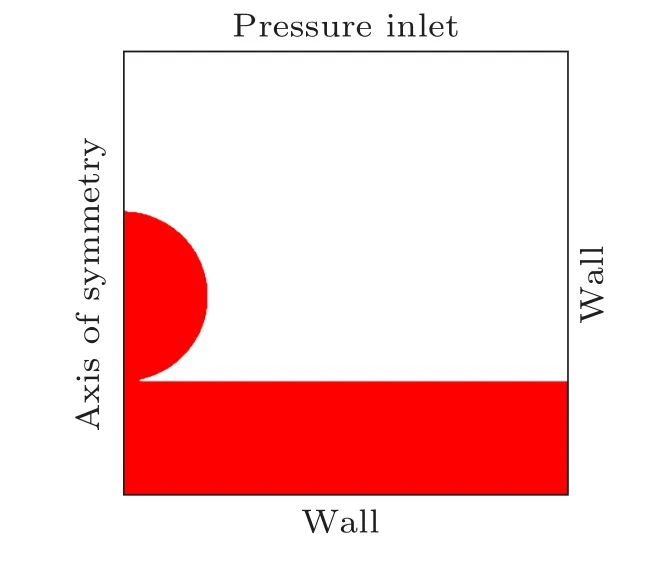
Fig.1. Schematic of the simulation system and boundary conditions.

2.2. Numerical method

The VOF method proposed by Hirt and Nichols[22]is adopted to track the interface.In this method,the volume fraction is introduced to describe different fluids

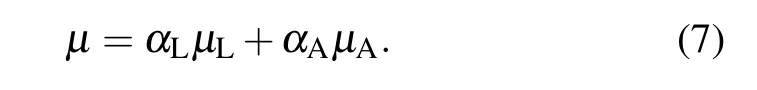
In the present study, the CFD software FLUENT is used to conduct the simulation. The geometric reconstruction scheme is chosen for the discretization of the VOF function.The PISO algorithm is selected for the pressure velocity coupling. The second-order upwind scheme is applied to discretize the spatial terms,while the first-order implicit method is adopted for the discretization of the transient terms. The PRESTO!scheme is used for the pressure interpolation.

2.3. Numerical model validation

The present numerical model is validated with the experimental result from Blanchette and Bigioni.[14]The ambient fluid is air; the droplet and underlying liquid is ethanol with the density of 786 kg/m3and the viscosity of 0.00105 Pa·s;the surface tension coefficient is 0.022 N/m;the initial droplet diameter is 1.07 mm. Figure 2 shows the comparison between experimental and numerical results. In the numerical simulation, the daughter droplet diameter ratio, defined as the ratio of the daughter droplet diameter to the initial droplet diameter,is 0.59, and the coalescence time, defined as the interval between the onset of coalescence and the pinch-off, is 3.72 ms.In the experiment of Blanchette and Bigioni,[14]the daughter droplet diameter ratio was 0.55 and the coalescence time was 3.98 ms. The discrepancies in the daughter droplet diameter ratio and coalescence time are 7.2% and 6.5%, which proves that the present numerical model is reliable.

3. Results and discussion

3.1. Daughter droplet diameter ratio and coalescence time

Firstly, three grid cases with the cell number of 76456,109600 and 171250 are used to examine the mesh independence. The results show that the discrepancy in the daughter droplet diameter between the grid cases with the cell number of 109600 and 171250 is less than 1%. Thus, the grid case with the cell number of 109600 is adopted in the following simulations.

The influence of droplet impact velocity on the daughter droplet diameter ratio is investigated,and the variation trend is shown in Fig.3. The initial droplet diameter is 3.82 mm. With the droplet impact velocity (U0) increasing from 0.01 m/s to 0.45 m/s, the daughter droplet diameter ratio decreases from 0.617 to 0.247 nearly linearly. When the droplet impact velocity increases to 0.455 m/s, the full coalescence happens, and no daughter droplet is pinched off. Different droplet impact velocities lead to different coalescence results: partial coalescence as shown in Fig.4(a)and full coalescence as shown in Fig. 4(b). And partial coalescence only takes place in a low impact velocity range.

Fig. 2. Comparison between the experimental result from Blanchette and Bigioni[14] (top rows) and numerical result in the present study (bottom rows). (a) 0.00 ms, (b) 0.53 ms, (c) 1.15 ms, (d) 1.40 ms, (e) 2.62 ms,(f)3.57 ms.

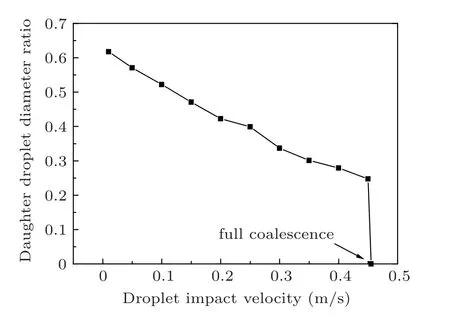
Fig.3. Daughter droplet diameter ratio vs. different droplet impact velocities.

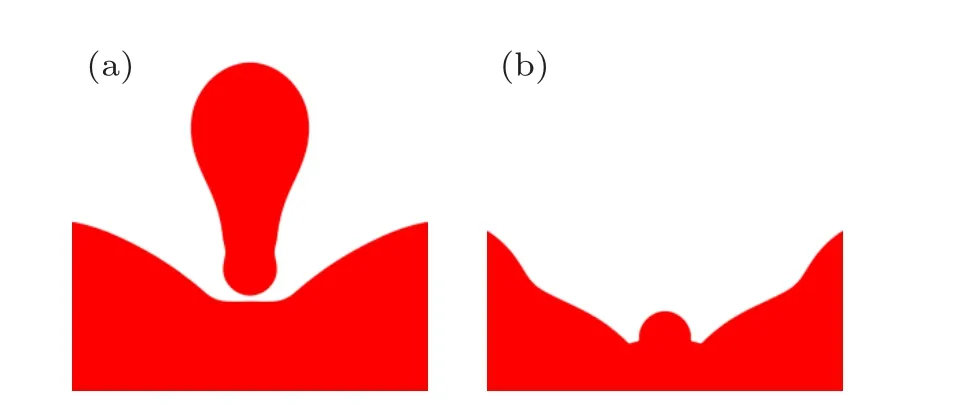
Fig. 4. Coalescence results with different droplet impact velocities. (a)partial coalescence with U0 = 0.05 m/s, (b) full coalescence with U0 =0.455 m/s.

The coalescence time is also a concerned parameter. Figure 5 shows the influence of the droplet impact velocity on the coalescence time. Similar to the variation trend of the daughter droplet diameter ratio, higher droplet impact velocity will result in shorter coalescence time. The coalescence time decreases from 14.67 ms to 9.30 ms,with the droplet impact velocity increasing from 0.01 m/s to 0.45 m/s. The reason is that higher droplet impact velocity will accelerate the coalescence process.

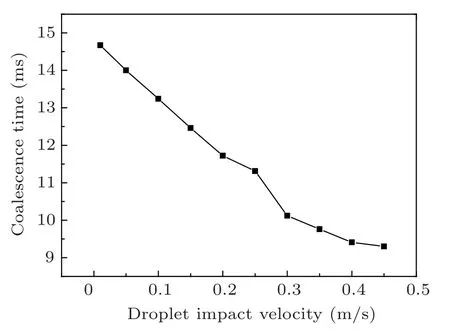
Fig.5. Coalescence time vs. different droplet impact velocities.

3.2. Mechanism of partial coalescence

Blanchette and Bigioni[14]suggested that the convergence of capillary waves was responsible for partial coalescence.However,we find that besides the capillary wave convergence,a downward high-velocity region at the neck also plays an important role. Figure 6 shows the pressure fields and velocity vectors at different moments during the partial coalescence process with the droplet impact velocity of 0.05 m/s.Note that there is a low-pressure region formed at the neck because of the negative curvature and surface tension. The velocity near the low-pressure region will be accelerated, and a downward high-velocity region arises.With the coalescence evolving,the high-velocity region expands, and the velocity magnitude increases,as shown in Fig.6. The high-velocity region will pull the droplet downward. And the capillary wave convergence can draw the droplet upward.[14]As a result, the droplet will change into a prolate shape. Since the high-velocity region with downward velocity stretches the droplet continuously,the neck becomes thinner and thinner and finally pinches off. According to the present simulation,both the capillary wave convergence and the high-velocity region play important roles in partial coalescence. Ray et al.[20]concluded that partial coalescence took place when the horizontal momentum exceeded the vertical momentum. Nevertheless,it is not a necessity for the pinch-off in the present simulation,since the vertical momentum dominates and the pinch-off still happens, as shown in Figs.6(g)and 6(h).

Figure 7 shows the evolution of minimal pressure in the low-pressure region. The evolution goes through three stages:increase stage,flat stage and decrease stage. At 1 ms,the minimal pressure reaches −358.7 Pa and then increases into a flat stage at about 4 ms. The flat stage lasts for 6 ms and then decreases to −399.4 Pa at 13 ms. The minimal pressure remains negative during the coalescence. The negative pressure results from the competition between the two curvature radiuses, R1and R2,as shown in Fig.6(c)and the negative curvature radius R2dominates during the coalescence.

Figure 8 shows the evolution of the maximum velocity in the high-velocity region. It can be seen that the maximum velocity increases continuously under the influence of the lowpressure region. The increase is mild during the increase and the flat stages of the pressure evolution. When it comes to the decrease stage,the velocity increases rapidly,which helps stretching the droplet as introduced above.

Figure 9 shows the evolution of the velocity at the droplet summit. The velocity at the droplet summit fluctuates and can be downward with positive velocity or upward with negative velocity. Note that the velocity changes from 0.47 m/s at 7 ms to −0.55 m/s at 8 ms. The fluctuation range reaches 1.02 m/s.The fluctuation is a result of the propagation of the capillary wave. When the capillary waves converge at the summit, the velocity can be accelerated and a crater at the top of the droplet is created,as shown in Fig.6(d)at 7 ms.Also,the velocity can be decelerated by the capillary wave, and the droplet summit is drawn upward as shown in Fig.6(e)at 9 ms.

Furthermore,it is found that the shift from partial coalescence to full coalescence with the increase of droplet impact velocity depends on the droplet shape before the pinch-off.Figure 10 shows the droplet shapes before the pinch-off with different droplet impact velocities. The moments are chosen when the radiuses of the neck for each case are the same.Note that the droplet shapes are prolate and with the droplet impact velocity increasing it will get close to a sphere as shown in Fig.10. Under the effect of surface tension,the prolate shape tends to evolve into a sphere,which is conducive to the shrinkage of the neck. As the droplet impact velocity increases,the shape gets closer to a sphere and the shrinking trend of the neck is diminishing. Thus, when the droplet shape is close enough to a sphere, the pinch-off stops to take place. The droplet shape can be evaluated by the ratio of the long axis length (a) to the theoretical droplet diameter (Dv) which is corresponding to the volume of the droplet (V) as shown in Fig. 10(a). The variation trend of the ratio (a/Dv) with the droplet impact velocity is shown in Fig.11. It can be seen that when the ratio is close to 1, which means the droplet shape is nearly a sphere the partial coalescence shifts to full coalescence.

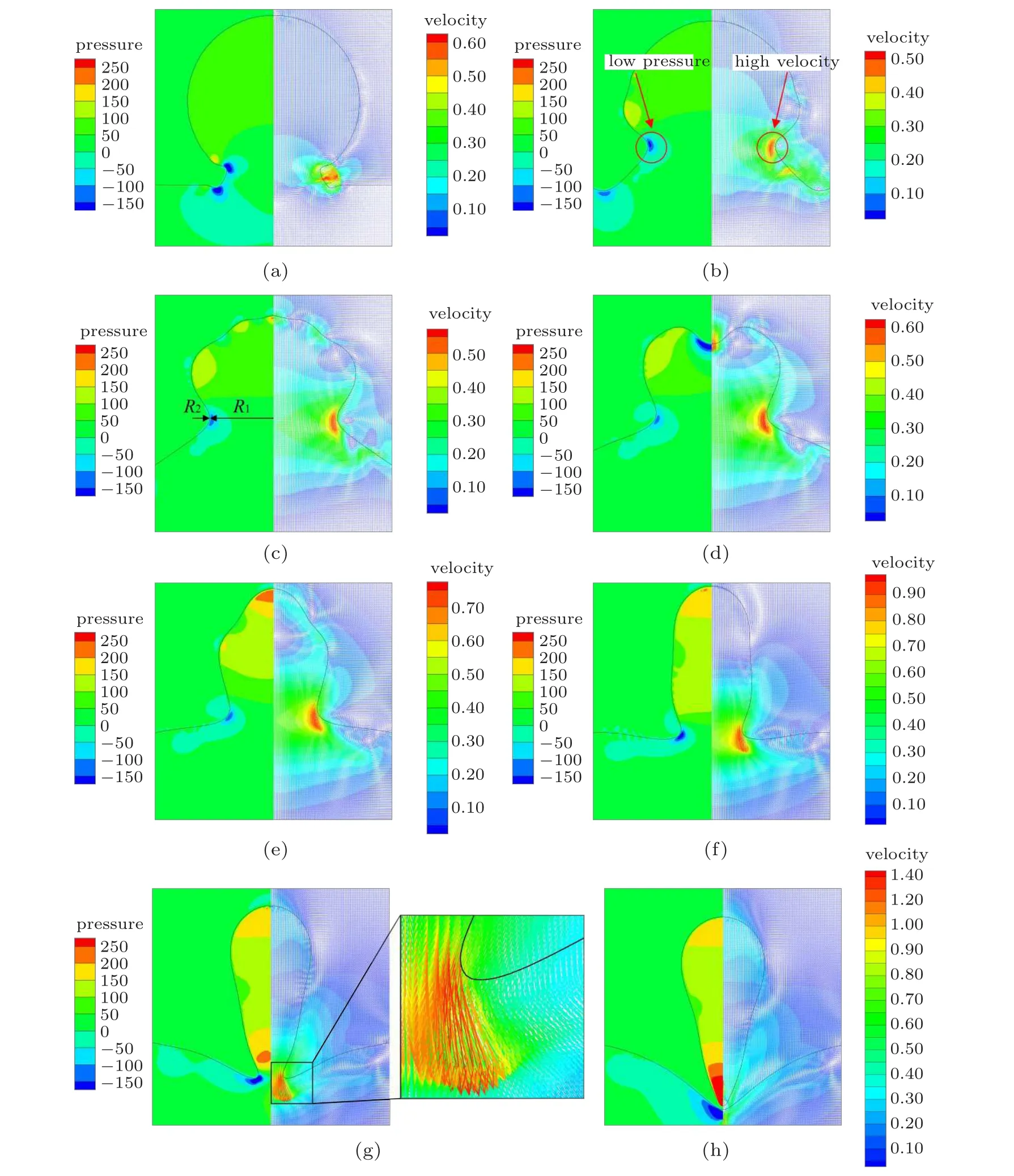
Fig.6. Evolution of the pressure field and velocity vector with the surface tension coefficient of 0.073 N/m and the droplet impact velocity of 0.05 m/s(pressure: Pa,velocity: m/s). (a)1 ms,(b)3 ms,(c)5 ms,(d)7 ms,(e)9 ms,(f)11 ms,(g)13 ms,(h)14 ms.

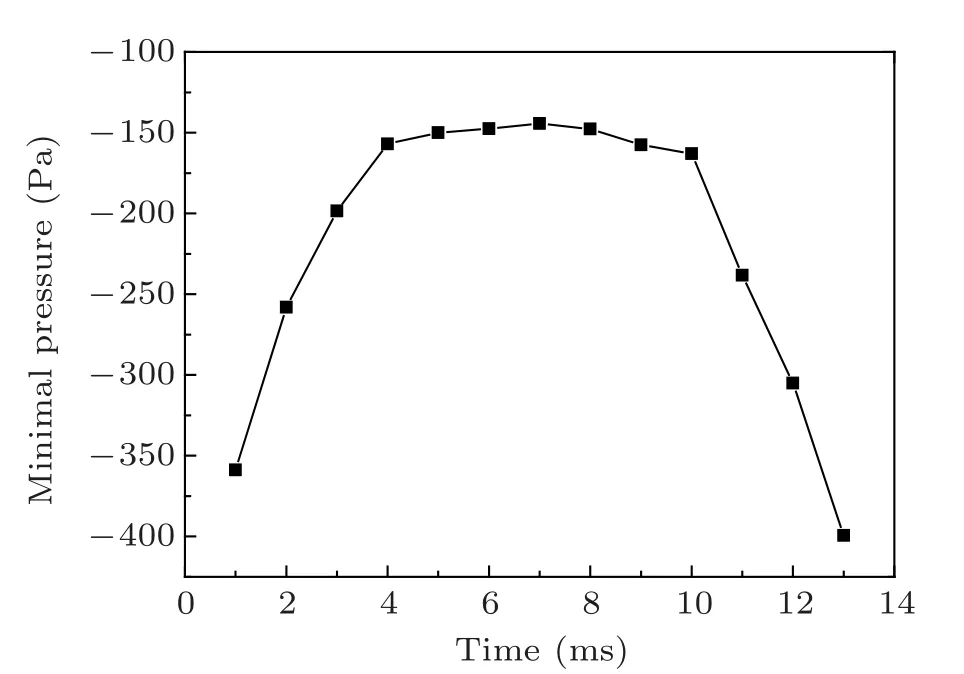
Fig. 7. Evolution of the minimal pressure in the low-pressure region with the surface tension coefficient of 0.073 N/m and the droplet impact velocity of 0.05 m/s.

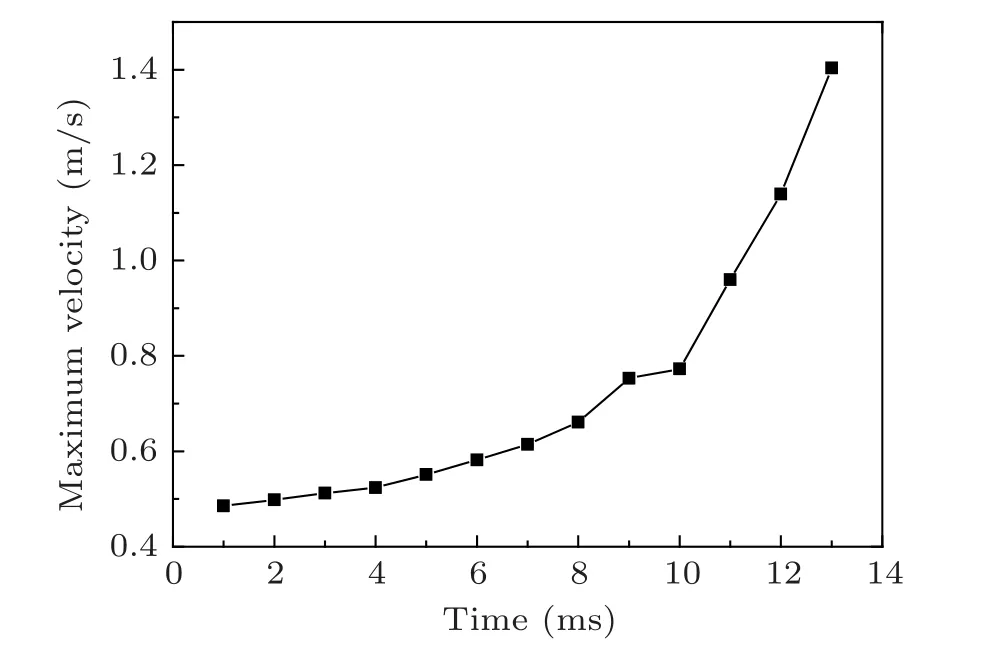
Fig.8. Evolution of the maximum velocity in the high-velocity region with the surface tension coefficient of 0.073 N/m and the droplet impact velocity of 0.05 m/s.

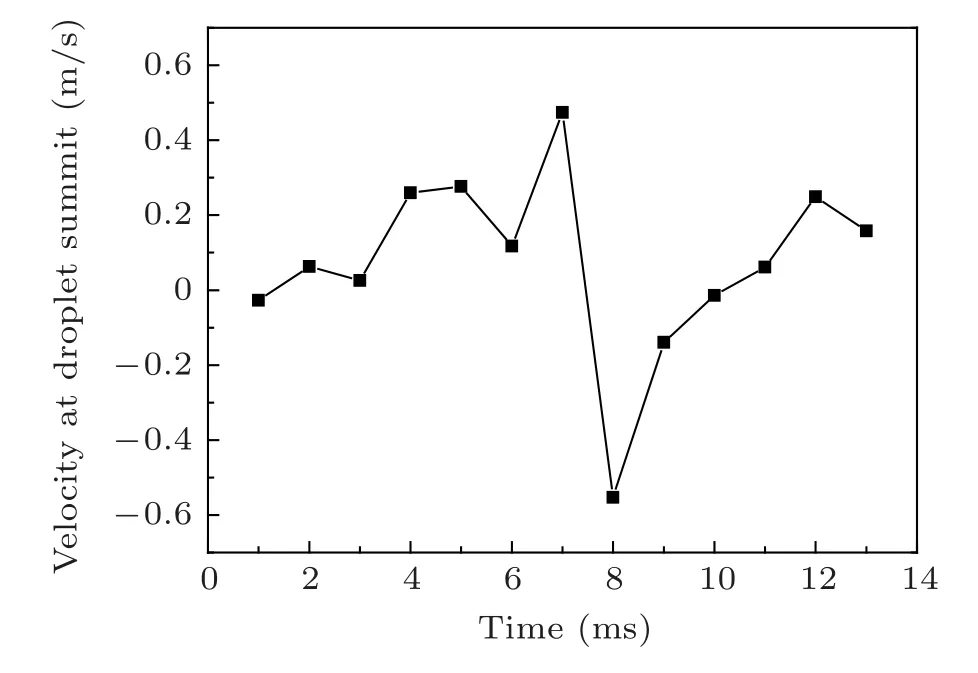
Fig.9. Evolution of the velocity at the droplet summit with the surface tension coefficient of 0.073 N/m and the droplet impact velocity of 0.05 m/s.

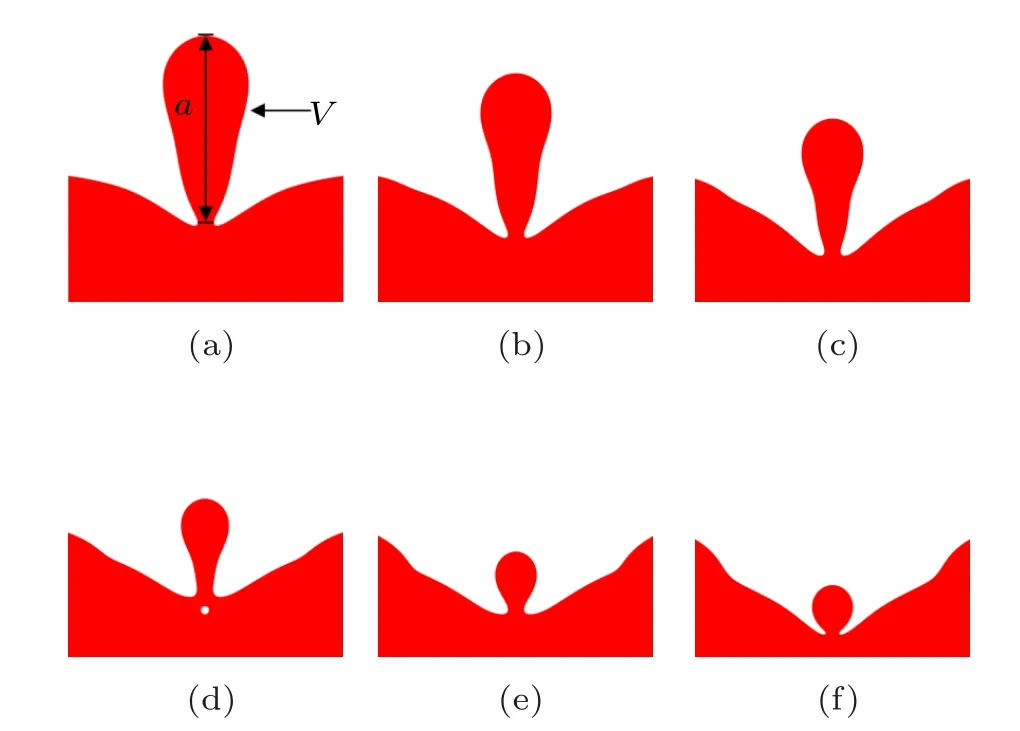
Fig.10. Shape of the droplet before the pinch-off with different droplet impact velocities. (a)U0=0.05 m/s,(b)U0=0.15 m/s,(c)U0=0.25 m/s,(d)U0=0.35 m/s,(e)U =0.45 m/s,(f)U =0.455 m/s.

Fig.11. The ratio of the long axis length to the theoretical droplet diameter which is corresponding to the volume of the droplet.

3.3. Effect of film thickness

In this section,the effect of film thickness(f0)on the coalescence is investigated. Figures 12 and 13 show the variation trends of the coalescence time and daughter droplet diameter ratio with the film thickness, respectively. It is noted that the film thickness has a slight influence on the coalescence time and daughter droplet diameter ratio when the film thickness is greater than 2.0 mm. However, with the decrease of the film thickness,full coalescence will happen. It can be explained with the evolution of the high-velocity region. Figure 14 shows the evolution of the maximum velocity in the high-velocity region with U0=0.1 m/s. It can be seen that in the case with the film thickness of 0.1 mm,the maximum velocity increases significantly slower than that in the cases with the film thickness of 0.5 mm, 1.0 mm, 2.0 mm and 3.0 mm.Partial coalescence happens in the cases with the film thickness of 0.5 mm,1.0 mm,2.0 mm and 3.0 mm,while full coalescence happens in the case with the film thickness of 0.1 mm.With the evolution of the high-velocity region, the droplet is stretched downward, and the liquid film is pushed away. A crater is created in the liquid film,as shown in Fig.6(h). If the film thickness is small,there will not be enough space for the evolution of the high-velocity region. That is, the small film thickness will suppress the high-velocity region. And the slow increase of the maximum velocity will retard the stretching of the droplet. As a result, full coalescence happens in the case with small film thickness.The results also imply that the highvelocity region plays a significant role in partial coalescence.

Fig.12. The effect of film thickness on coalescence time.

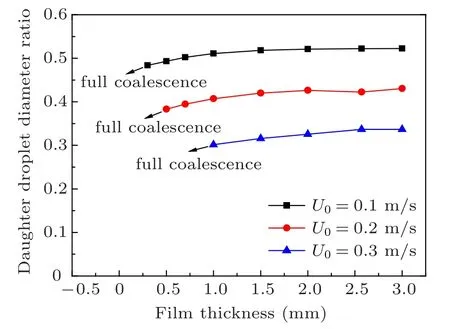
Fig.13. The effect of film thickness on daughter droplet diameter ratio.

3.4. Critical droplet impact velocity

According to the investigation above, there is a critical droplet impact velocity for partial coalescence to take place.When the droplet impact velocity is higher than the critical droplet impact velocity, partial coalescence will shift to full coalescence. In this section,the effects of surface tension coefficient, viscosity, and initial droplet diameter on the critical droplet impact velocity are discussed.

Figure 15 shows the variation trend of the critical droplet impact velocity with surface tension coefficient. The droplet diameter is 3.82 mm and the viscosity is 0.001 Pa·s. The numerical results indicate that the critical droplet impact velocity increases with the increase of surface tension coefficient. That is, the shift from partial coalescence to full coalescence with a higher surface tension coefficient happens at higher droplet impact velocity. The coalescence process is affected by multifactors. Low droplet impact velocity leads to partial coalescence,while high droplet impact velocity leads to full coalescence. That is, the larger inertia force inhibits partial coalescence. On the contrary,higher surface tension is beneficial for the shrinkage of the neck of the droplet and will promote the final pinch-off. With a higher surface tension coefficient, the surface tension can dominate at a higher droplet impact velocity. As a result,the pinch-off can take place at a higher droplet impact velocity.

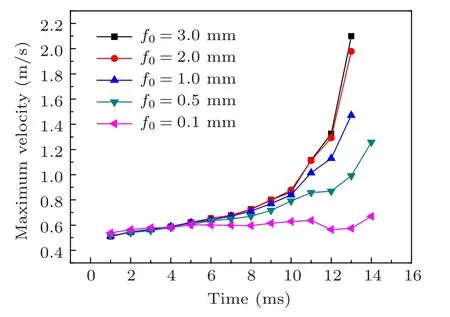
Fig.14. The effect of film thickness on the evolution of the maximum velocity in the high-velocity region with U0=0.1 m/s.

Fig.15. The effect of surface tension coefficient on the critical droplet impact velocity.

Figure 16 shows the effect of viscosity on the critical droplet impact velocity. The droplet diameter is 3.82 mm,and the surface tension coefficient is 0.073 N/m. Unlike the variation trend with surface tension coefficient, the critical droplet impact velocity decreases with the increase of viscosity. The reason is that higher viscosity will inhibit the capillary wave[14]and damp the velocity of the droplet during the coalescence. As a result, the stretching of the droplet is retarded, and it is easier for full coalescence to take place at lower droplet impact velocity.

Figure 17 shows the effect of initial droplet diameter on the critical droplet impact velocity. The surface tension coefficient is 0.073 N/m, and the viscosity is 0.001 Pa·s. Similar to the variation trend with viscosity,the critical droplet impact velocity decreases with the increase of initial droplet diameter.The reason is that with a larger droplet diameter, the inertia force which inhibits partial coalescence is larger,while the effect of surface tension which promotes partial coalescence is weaker. In other words,the inertia force with a larger droplet diameter can dominate at lower droplet impact velocity.

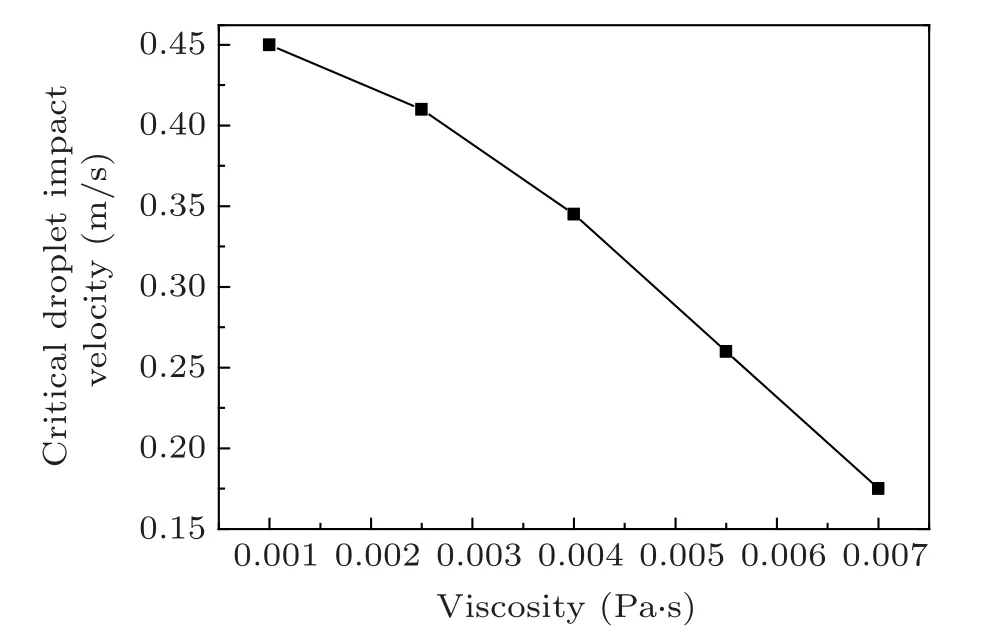
Fig.16. The effect of viscosity on the critical droplet impact velocity.

Fig.17. The effect of initial droplet diameter on the critical droplet impact velocity.

The critical droplet impact velocity is used to calculate the critical Weber number (Wec) defined as ρLU2cD0/σ. Ucis the critical droplet impact velocity, and D0is the initial droplet diameter. Figures 18–20 show the effects of surface tension coefficient, viscosity, and initial droplet diameter on the critical Weber number, respectively. It can be seen that the critical Weber number decreases with the increase of viscosity monotonically. Different from the variation trend with viscosity,the critical Weber number increase with the increase of surface tension coefficient and initial droplet diameter nonmonotonically. As the surface tension coefficient or the initial droplet diameter increases, there is a maximum value for the critical Weber number.

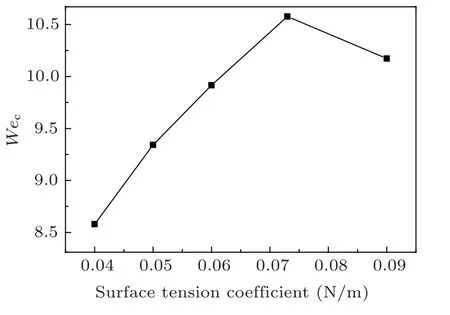
Fig. 18. The effect of surface tension coefficient on the critical Weber number.

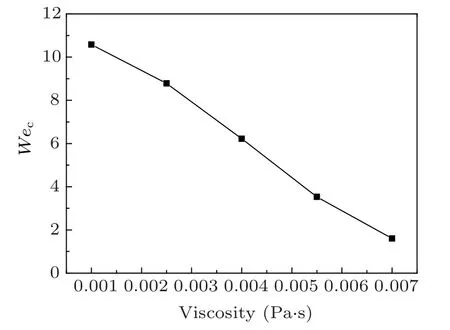
Fig.19. The effect of viscosity on the critical Weber number.

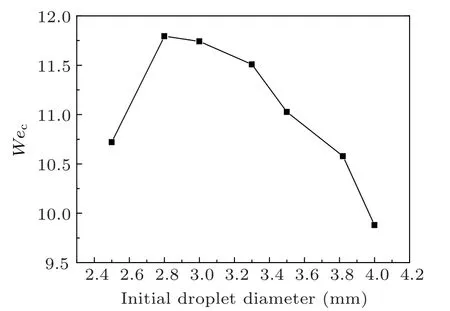
Fig.20. The effect of initial droplet diameter on the critical Weber number.

4. Summary and conclusion

In the present study, the VOF method is adopted to simulate the partial coalescence process. The importance of a downward high-velocity region formed near the low-pressure region for the droplet evolving into a prolate shape and the final pinch-off is proposed. The low-pressure region is caused by the negative curvature and surface tension. Furthermore,the shift from partial coalescence to full coalescence is explained based on the droplet shape before the pinch-off. The droplet shape is evaluated by the ratio of the long axis length of the prolate droplet to the theoretical droplet diameter which is corresponding to the volume of the droplet. With the increase of droplet impact velocity, the droplet shape will get close to a sphere. When the droplet shape gets close enough to a sphere, the shrinking trend of the neck is weak, and the partial coalescence will shift to full coalescence. The effect of film thickness is also studied. When the film thickness is large enough,the film thickness shows a slight influence on the coalescence, and when the film thickness is small, the full coalescence rather than partial coalescence happens. Moreover,the influences of surface tension coefficient,viscosity,and initial droplet diameter on the critical droplet impact velocity are investigated. The results show that a higher surface tension coefficient will cause higher critical droplet impact velocity while higher viscosity and larger droplet diameter will lead to lower critical droplet impact velocity. The critical droplet impact velocity is used to calculate the critical Weber number.The results indicate that there is a maximum critical Weber number with the increase of surface tension coefficient and initial droplet diameter.