Reputational preference and other-regarding preference based rewarding mechanism promotes cooperation in spatial social dilemmas*

Huayan Pei(裴华艳), Guanghui Yan(闫光辉),†, and Huanmin Wang(王焕民)

1School of Electronic and Information Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

2Mechatronics T&R Institute,Lanzhou Jiaotong University,Lanzhou 730070,China

Keywords: cooperation,rewarding mechanism,reputational preference,other-regarding preference

1. Introduction

Cooperation,which means individuals working together,is widespread in nature and human society. Cooperation can be simply defined as a cooperator incurs a cost to benefit others, while a defector tries to gain benefit without providing help to others.[1]Therefore, it will be beneficial for the welfare of the group if an individual chooses cooperation, while it will be more profitable for oneself if an individual selects defection. As a result,cooperation is prone to exploitation by selfish individuals.[2]Thus, the problem of how cooperation emerges and evolves is a topic of interest to researchers from diverse fields.[3–5]

Over the past decades, evolutionary game theory[6–8]has been developed into a powerful approach to investigate the evolution of cooperation in various social, economic and biological settings.[9–12]Furthermore, in order to model cooperation dilemmas, diverse game models have been proposed,[13–15]including prisoner’s dilemma game(PDG),[16–18]public goods game(PGG),[19–21]and snowdrift game(SDG).[22–24]PDG has been widely used to explore the emergence of cooperative behavior. In a two-strategy PDG,two players simultaneously decide whether to cooperate (C)or to defect(D). On mutual cooperation,each player gains R.Upon mutual defection, every player acquires P. If the two players choose distinct game strategies, then the cooperator gets S, and the defector obtains T. The existence of a PDG fulfills two conditions: T ＞R ＞P ＞S and 2R ＞T+S,which implies that defection–defection is the only Nash equilibrium.

In the real world, interactions among individuals are not random,each individual can only interact with a small number of others who are closely connected to him.In other words,interactions among individuals are often exquisitely structured.As pioneers,Nowak and May originally proposed spatial game theory by integrating spatial structure with the PDG,[25]in which players are situated on the nodes of a square lattice,and edges between nodes representing game interactions between players. Compared with the unweighted networks, the weighted networks can better characterize the heterogeneity of interaction relationships between players. In particular,the weighted networks based on vertex weight can better characterize the heterogeneity of individuals’social influence or social preference.[26]In evolutionary games on graphs, natural selection favors defection,for cooperation to emerge,a mechanism for the promotion of cooperation is needed. During the past two decades,a wide range of mechanisms have been proposed to promote the evolution of cooperation, including image scoring,[27]reputation,[28]teaching activities,[29]reward[21]and punishment,[30,31]spatial structure in memorybased SDG,[32]compassion,[33]transaction costs,[34]deposit mechanism,[35]benefit community,[36]and break and establishment of links, etc.[37]Typically, Nowak proposed five rules[38]for the evolution of cooperation, which includes indirect reciprocity.[39–42]As one of the crucial mechanisms for evaluating trust,reputation not only fuels the engines of indirect reciprocity,[38]but also builds up trust,which is a precondition of cooperation.[43]Moreover, it has been revealed that people commonly take reputational information into consideration in deciding how to interact with others.[44–46]In other words, individuals probably have reputational preference in social interactions. The main exhibition is that people prefer to help individuals who have good reputation,but may refuse to provide help to others with bad reputation.

In the traditional evolutionary game theory, it is commonly assumed that individuals are rational and egoistic,that is to say, individuals only care about their own benefit. Nevertheless,other behaviors that are distinct from self-regarding ones have been found in behavioral science and experimental economics. These behaviors can be referred to as otherregarding preference, which is originally proposed by Maynard Smith[6]and Grafen[47]in the investigation of animal behaviors between relatives. Then, Taylor and Nowak[48]formalize it as a model to capture the group- and kin-selection mechanisms. Other-regarding preference has been used to update strategy in few works.[49,50]Inspired by these works,we propose a preference rewarding mechanism by incorporating vertex weight into the spatial prisoner’s dilemma game. The vertex weight of a player is adaptively adjusted by comparing his own reputation and the average reputation value of his immediate neighbors. Players are willing to reward the cooperative neighbor who has the greatest vertex weight at a personal cost. Most noteworthy, the rewards are dynamically adjusted according to the adaptive adjustment of vertex weight and the update of game strategy.

A variety of previous works have studied the impacts of reputation on the emergence of cooperation, which primarily concentrate on PGG[39,51]and PDG.[28,52]Especially, Fu et al. revealed that cooperation flourishes when individuals are able to change interaction relationships and game strategies on the basis of reputation.[28]Later, Li et al. found that the adaptive adjustment of link weight caused by reputation alteration greatly facilitates the evolution of cooperation.[52]Meanwhile, several other works have investigated the effects of rewarding mechanism on the evolution of cooperation based on PGG,[19,21]the results show that rewards can give rise to cooperation in the context of a public goods experiment. Rewards indicate paying a cost to benefit others. In these works,the rewards are mainly coming from social institutions[19]and rewarding cooperators.[21]In particular, Andreoni et al. explored demands for rewards and punishments,as well as their effects on cooperation in a proposer-responder setting.[53]They revealed that it is important that both tools be present when devising incentive systems.

In this work,our aim is to study the impact of preference rewards on the evolution of cooperation. Notably, the preference rewards are mainly deriving from reputational preference and other-regarding preference. Under the preference rewarding mechanism, players are willing to sacrifice personal payoff to reward the cooperative neighbor with the largest vertex weight. To the best of our knowledge, preference rewards simultaneously consider reputational preference,otherregarding preference and the dynamic adjustment of vertex weight has not been reported before. The primary difference between the preference rewarding mechanism and the other rewarding mechanisms is that the preference rewards are coming from one’s nearest neighbors who have reputational preference and other-regarding preference. Simulation results reveal that under the proposed rewarding mechanism,both the microlevel cooperative behavior of individuals and the macro-level cooperation level of the whole system are extremely advanced.It is worth stressing that the dynamic adjustment of vertex weight plays an essential role on the promotion of cooperation. Furthermore,the preference rewarding impact factor has positive effect on the emergence of cooperative behavior.

This article is organized as follows. The model is briefly introduced in Section 2. The simulation results and discussions are presented in Section 3. Conclusions are drawn in Section 4.

2. Model

In the present work,in order to focus on the preference rewarding mechanism and to avoid the influence of heterogeneity of network structure,we consider primarily the spatial PDG on L×L regular square lattice with periodic boundary condition,where each node equally has four fixed immediate neighbors. Initially, each player is randomly designed to be either a cooperator(C,s=[1,0]T)or a defector(D,s=[0,1]T)with equal probability. Parameters setup of the PDG payoff matrix is in line with the previous works:[25,54]R=1, P=S =0,and T =b(1 ＜b ＜2),thus the 2×2 payoff matrix M is controlled by a single parameter b,which represents temptation to defect:[25,55]

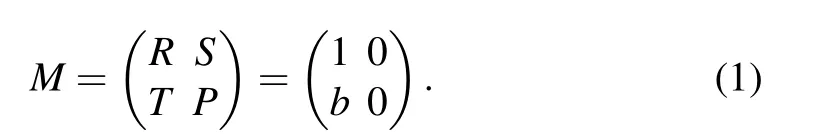
The game proceeds in accordance with the Monte Carlo simulation. Originally, 50% players are assigned to be randomly distributed cooperators.

Firstly, for each player, his payoff is the total payoffs gained from playing PD games with direct neighbors, which can be written as

where Ωxdenotes the neighborhood set of player x.The strategies of x and his neighbor y are represented by sxand sy,respectively. The total number of time player x cooperates with nearest neighbors in the past games is defined as his reputation at time t,[28]which reads

where parameter ΔR denotes the reputation value player x obtains through a single game round, if x chooses C strategy at time t then ΔR=1, otherwise ΔR=0. Initially, the reputation score for cooperators and defectors are set to be 1 and 0,respectively.

Secondly, at each game iteration, the reputation score of a player is calculated according to Eq.(3). Then,the average reputation value of player x’s direct neighbors at time t can be computed by

where parameter kxrepresents the full number of x’s direct neighbors.

In the real world, an individual impacted by otherregarding preference is willing to pay a personal cost to reward the cooperative neighbor. Furthermore, since reputational information is taken into account by people in deciding how to interact with others.[44–46]Therefore,in deciding which neighbor should be rewarded,a player probably tends to reward the cooperative neighbor who has the highest reputation score in the past games. Thus,we introduce vertex weight wxinto the traditional PDG to characterize the intensity of player’s preference rewarding willingness for distinct neighbors. The dynamic adjustment of vertex weight can characterize the heterogeneity of preference rewarding willingness. To be specific,if player x’s reputation score is greater than the average reputation value of his immediate neighbors,then the vertex weight wxwill be increased by one unit,denoting that neighbors’rewarding willingness for x is strengthened,otherwise it will be decreased by one unit,representing that the rewarding willingness is weakened. If player x’s reputation value is equal to the average one,then the vertex weight wxwill be kept for the next game iteration. Therefore,the adjustment of vertex weight wxat time t can be defined as

Following the range setup of link weight in previous works,[56,57]we assume that the vertex weight falls within the range of [1 −ε,1+ε]. Parameter ε ∈[0,1) determines the limit value of the vertex weight. The model will be turn to the traditional PDG when ε =0. However, when ε /=0, the heterogeneity of vertex weight will be introduced into the model.Without loss of generality,initially the equal weight=1 is designated to each vertex. During the co-evolutionary process,the vertex weight will be dynamically adjusted according to the alteration of reputation caused by strategy update.

Thirdly,at each game iteration,every player has a chance once on average to update his vertex weight according to Eq. (5). Under the preference rewarding mechanism, each player chooses the cooperative neighbor with the largest vertex weight to reward. Assume that there are more than one neighbors with the greatest vertex weight in the neighborhood,then one of them is randomly selected to reward.Nevertheless,there are other impact factors affecting the rewards one player can give to the mentioned cooperative neighbor,such as one’s education level and financial situation. Hence,we bring in another parameter δ to characterize the effect of other impact factors on the preference rewards. Then the fitness of player x and his neighbor y can be defined as

where δ ∈[0,1] represents the preference rewarding impact factor. The model will be reduced to the original PDG when δ=0,which implies that the preference rewarding mechanism is not involved.

Fourthly,at every game round,each player has an opportunity once on average to update the fitness of his own and the rewarded cooperative neighbor according to Eq.(6). Ultimately,at every full MCS step,each player has a chance once on average to update his strategy. To be specific,player x randomly selects one neighbor y, and x adopts the strategy of y with a probability given by the Fermi function[54]

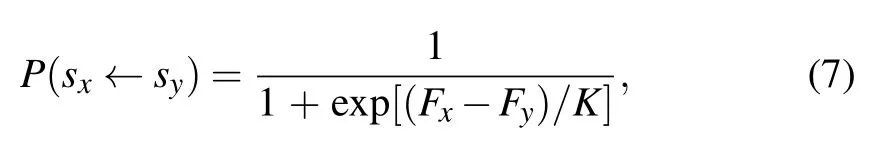
where K(K ＞0)represents the intensity of selection, K →0 implies the deterministic imitation dynamics, whereas K →+∞indicates complete randomness. Consistent with previous works,K is set to be 0.1 in our model.

After the above-mentioned five steps are finished, a full Monte Carlo simulation (MCS) procedure is completed. The numerical results were obtained on a square lattice with 2500 nodes. The total number of MCS time steps is set to be MCS = 1×104. The main quantity to characterize the cooperative behavior is the average fraction of cooperators ρcin the population, which was calculated within the last 103full MCS time steps after the system reaching equilibrium. Furthermore, all data were averaged over up to 20 independent runs to alleviate the effect of disturbances. In addition, players are assumed to have memory of two game steps as well as selection preference.

3. Simulation results and discussion

In Fig. 1, we uncover the relationship between the fraction of cooperators ρcand temptation to defect b under different parameter ε and the preference rewarding impact factor δ.Clearly,for fixed δ,cooperators’frequency displays a significant rise with increasing ε,implying that the adaptive adjustment of vertex weight dramatically favors the emergence of cooperation. Looking at a specific instance,the threshold between full cooperation(C)and the coexistence state of cooperators and defectors(C+D)is increased from 1.05[panel(a)]to 1.15[panel(d)]when ε is increased from 0 to 0.9 at δ =0.5.Correspondingly, the threshold between C+D and pure D is risen from 1.5 to 2. Moreover,irrespective of ε,cooperators’density decreases with increasing b,indicating that the rise of temptation to defect inhibits the emergence of cooperative behavior. Typically, the percentage of cooperators dramatically drops to zero when the preference rewarding mechanism is absent(δ =0). However,the threshold of cooperation vanishing is increased with rising preference rewarding impact factor δ,implicating that the preference rewarding impact factor greatly facilitates the survival of cooperators. At ε =0.6[panel(c)],for instance,the threshold of full cooperation extinction is increased from 1.025 to 1.35 as δ varies from 0.2 to 1. Similar phenomena can be seen in other panels.

Fig. 1. Fraction of cooperators ρc as a function of temptation to defect b under distinct values of parameter ε and the preference rewarding impact factor δ (a)ε =0;(b)ε =0.3;(c)ε =0.6;(d)ε =0.9. It can be observed that the cooperation level shows a decrease with the rise of temptation to defect b. Other parameters are set to be L=50 and K=0.1.

In Fig.2,we investigate the correlation between the percentage of cooperators ρcand the preference rewarding impact factor δ under distinct parameter ε and temptation to defect b.Obviously,for fixed b,smaller values of δ is able to promote the emergence of cooperative behavior when parameter ε is increased,which reveals the significant influence of the adaptive adjustment of vertex weight on the promotion of cooperation.Taking an example,the value of δ that drives cooperation emergence is declined from 0.225[panel(a)]to 0.1[panel(d)]as ε is risen from 0 to 0.9 at b=1.2. Also, the threshold between the coexistence state and pure cooperation is decreased from 0.95 to 0.55. Furthermore, when temptation to defect b equals cooperation reward(b=1),cooperators can occupy the whole population even if δ is quite small. Most importantly,when b is fixed, cooperators’ frequency shows a rising trend with increasing δ, which further validates the crucial role of preference rewarding impact factor in promoting cooperation.Looking at a specific instance,at ε =0.6[panel(c)],cooperative behavior is significantly fostered for proper values of δ,although the threshold of cooperation emergence is increased from 0.125 to 0.5 when b is increased from 1.2 to 2.

To explore the effect of the adaptive adjustment of vertex weight and the preference rewarding impact factor δ on the evolution of cooperation,the contour plot in the b–δ plane for the evolution of ρcis presented in Fig. 3. Most noteworthy,when parameter ε is increased from 0[panel(a)]to 0.9[panel(b)],the cooperation level is dramatically enhanced,indicating that cooperators are easier to survive if the vertex weight is dynamically adjusted. This is mainly because the adjustment of vertex weight drives the rising of preference rewards, which lead to the emergence of cooperative behavior. Importantly,the cooperation level is significantly advanced with the rise of δ, which confirms the essential role of preference rewarding impact factor in facilitating cooperation in Fig.2. That is,under the preference rewarding mechanism,a defector is willing to reward the cooperative neighbor with the greatest vertex weight by distributing a proportion of his payoff to the neighbor. As a result,cooperators have great advantage over defectors after receiving rewards,then more players prefer to choose C strategy, that is why cooperation prevails. In contrast, with increasing temptation to defect b, cooperative behavior is extremely inhibited and does not have the chance to thrive,since defectors become more favorable by natural selection as b increases. The results indicate that with ever-rising temptation to defect b,merely the preference rewarding mechanism is not sufficient to support the persistence of cooperation when the preference rewards are small.

Fig.2. Fraction of cooperators ρc as a function of the preference rewarding impact factor δ under different values of temptation to defect b and parameter ε: (a)ε=0,(b)ε=0.3,(c)ε=0.6,(d)ε=0.9. The data show that the cooperation level displays a significant rise with increasing δ. Other parameters are fixed to be L=50 and K=0.1.

Fig.3. Contour plots for the fraction of cooperators ρc in the parameter plane b–δ under distinct values of parameter ε: (a)ε =0,(b)ε =0.9.It can be seen that the cooperation level is significantly promoted with the rise of rewarding impact factor δ,while it is greatly inhibited with increasing temptation to defect b. Other parameters are set to be L=50 and K=0.1.

To further illustrate the joint effects of the adaptive adjustment of vertex weight and the preference rewarding impact factor δ on the emergence of cooperation, the contour plot in the ε–δ plane for the evolution of ρcis shown in Fig.4.Obviously, with the increase of ε and δ, the whole transition process from pure defection to the coexistence state of cooperators and defectors,and then to full cooperation can be found.Noteworthy, for fixed b, both rising ε and δ significantly favor the prevalence of cooperative behavior. Nevertheless, the speed of cooperation emergence is greatly suppressed when b is risen from 1.2[panel(a)]to 1.5[panel(b)].In our model,the vertex weight of a player is proportional to the preference rewards he can obtain from direct neighbors,which falls within the range of [1+ε, 1 −ε]. With the adaptive adjustment of vertex weight,the preference rewards a cooperator gains from a wealthy defective neighbor is increased when ε becomes larger, that is why higher cooperation level can be driven by the dynamic adjustment of vertex weight. Furthermore, the preference rewards are increased with the rise of preference rewarding impact factor, then the fitness of cooperators becomes higher than that of defectors, that is the main reason for the prevalence of cooperation. Altogether, it is the joint impacts of the adaptive adjustment of vertex weight and the preference rewarding impact factor δ that facilitate the density of cooperators into a higher level. In addition,the results show that cooperation is much less favored when the preference rewarding mechanism is absent(δ =0).

In Fig.5,we inspect the characteristic snapshots between cooperators and defectors in a microscopic view. In the first row of panels, the setup of the two parameters is ε =0 and δ = 0.2, indicating that the influence of the preference rewarding mechanism is little. In such a case, initially, cooperators and defectors coexist with equal percentage at t=0,then cooperators gradually decrease with MCS time steps and eventually become extinction,which implies that it is hard for cooperators to survive when the preference rewards are small.However,the unfavorable situation for cooperators is dramatically improved when ε is risen(the second line of panels),and small cooperative clusters can be observed at t=10. Furthermore, with rising δ (the third line of panels), larger cooperative clusters emerge at t =50. Then with the further increase of ε (the fourth line of panels),giant cooperative clusters can be seen at t =50. By comparing different rows of panels,we find that it is easier for cooperators to agglomerate if the value of ε or δ becomes greater. The results show that under the joint effects of the adaptive adjustment of vertex weight and the preference rewarding impact factor δ, cooperators accumulate great advantage to defend the invasion of defectors and eventually occupy the entire system. That is the leading cause for the evolution of cooperation.

Fig.4. Contour plots for the fraction of cooperators ρc in the parameter plane ε–δ under different temptations to defect b: (a) b=1.2, (b)b=1.5. It can be found that the cooperative behavior is effectively facilitated with the increase of parameter ε and the preference rewarding impact factor δ. Other parameters are fixed to be L=50 and K=0.1.

Fig.5. Characteristic snapshots between cooperators(red)and defectors(green)for different values of parameter ε and preference rewarding impact factor δ. From top to bottom, ε and δ are set to be ε =0, δ =0.2; ε =0.5, δ =0.2; ε =0.5, δ =0.5; ε =0.9, δ =0.5; ε =0.9,δ =0.7,respectively. Other parameters are set to be L=50 and K=0.1. Each row in Fig.5 is taken from a single run.

In Fig. 6, we examine the transition frequencies of C →C(TCC), D →D(TDD) and D →C(C →D)(TDC) strategy pairs as a function of the preference rewarding impact factor δ under distinct parameter ε and temptation to defect b. The frequencies of these three kinds of transitions can be computed by

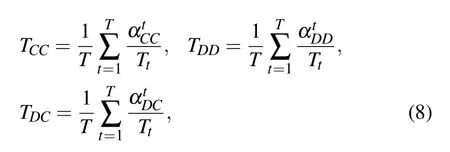
Finally,in Fig.7,we uncover the average payoff and fitness of cooperators and defectors in a microcosmic perspective. Obviously, with time going, both PDand FDrapidly fall to zero at ε =0 and δ =0.2[panel(a)], then PCand FCalso decline to zero,implying that the preference rewarding mechanism is insufficient to support the sustainability of cooperation when the preference rewards are small. However, greater PCand FCcan be found with rising ε [panels (b) and (d)] or increasing δ [panel(c)]. This is primarily because the adaptive adjustment of vertex weight leads to the increase of preference rewards, then more individuals are willing to choose C strategy. Interestingly, before cooperators dominating the whole population, it can be observed that both PDand FDare maintained at a steady level when the system reaching stable state[panels (b) and (c)]. This is mainly because larger ε and δ significantly promote the emergence of cooperation. Then a survived defector probably obtains benefit from nearest cooperative neighbors,which guarantees the survival of defectors.Nevertheless, when parameter ε and the preference rewarding impact factor δ are further increased, under the influence of the preference rewards, cooperators become evolutionarily competitive and ultimately occupy the whole population[panel(d)].

Fig.6. Transition frequencies of distinct strategy pairs as a function of the preference rewarding impact factor δ under different temptations to defect b and parameter ε: (a)ε =0,b=1.2;(b)ε =0.9,b=1.2;(c)ε =0,b=1.5;(d)ε =0.9,b=1.5. Other parameters are fixed to be L=50 and K=0.1.

Fig.7. Average payoff(PC,PD)and fitness(FC,FD)of cooperators and defectors at each time step. Parameter ε and the preference rewarding impact factor δ are set to be(a)ε =0,δ =0.2;(b)ε =0.5,δ =0.2;(c)ε =0.5,δ =0.7;(d)ε =0.9,δ =0.7,respectively. Other parameters are set to be L=50,K=0.1 and b=1.2.

4. Conclusions

In summary, we have proposed a preference rewarding mechanism in the spatial PDG to investigate the emergence and evolution of cooperative behavior. In our model, reputational preference,other-regarding preference and the dynamic adjustment of vertex weight are concurrently taken into account. The preference rewards mainly originate from reputational preference and other-regarding preference. Under the preference rewarding mechanism, players are willing to sacrifice personal payoff to reward the cooperative neighbor who has the largest vertex weight. It is worth noting that the rewards are dynamically adjusted in accordance with the alteration of vertex weight and the update of game strategy. The fitness of a player is determined by the union of his current payoff and the preference rewards he obtains from immediate neighbors. Simulation results reveal that the preference rewarding mechanism dramatically promotes the evolution of cooperation,both the adaptive adjustment of vertex weight and the preference rewarding impact factor have positive effects on the emergence of cooperative behavior. Moreover,to validate the above outcome,we have further analyzed the characteristic snapshots and the average payoff and fitness of cooperators and defectors in a microcosmic perspective,as well as the transitions frequency of different strategy pairs. The current results may supply a new perspective in establishing incentive mechanisms of cooperation.