一种抗冲击四节点柔性关节的设计与分析*
2021-05-24孙增晖张洪国
孙增晖,刘 宁,张洪国
(1.长春职业技术学院 机电学院,吉林 长春 130022;2.中车长春轨道客车股份有限公司,吉林 长春 130022)
0 引 言
资料显示,目前卒中已经成为全球第2大致死原因,且超过80%的中风幸存者患有某些类型的运动障碍[1]。卒中患者为改善生活质量,需长期进行康复训练。目前,患者康复疗法多选择接受治疗师辅助治疗,但康复治疗师资源匮乏。一方面,康复治疗师的工作需要花费大量时间,但是治疗效率低下;另一方面,康复治疗师无法获得定量的康复训练数据,无法掌握康复训练的效果[2]。近年来,康复技术有了长足的发展,但人机交互功能差,运动的精度差,容易对患者造成二次损害。
机器人技术与康复医疗的结合是过去20年的热门研究课题。随着机器人和康复技术的发展取得了巨大进步,康复机器人可以辅助患者完成四肢康复训练,并且将训练信息反馈给医生。不过,即便康复机器人发展迅速,还有许多尚未解决的问题,其中一个关键问题就是康复机器人的机械关节与人体关节的同步运动问题[3]。人与人之间的骨骼差异和人体关节的运动复杂性都会对机械关节和人体关节的同步运动造成影响。在这种情况下,康复机器人可能会使人体感觉不适或对人体造成伤害。加拿大多伦多大学KAN P等[4]研制了一种2自由度上肢平面康复机器人系统,用于手臂康复训练。英国南安普顿大学的CAI Z等[5]研制了5自由度的SAIL上肢康复机器人,在肩、肘转动关节装有扭簧弹性辅助支撑上臂质量,无驱动。
针对康复训练的要求,为解决震动和装配产生的内应力,笔者设计一种新型的柔性康复机械手臂装置,其装置将柔性四节点扭力弹簧与齿轮相结合,用于吸收关节震动、储存释放装置的能量,使整个装置运动更加平稳,更能提升患者对机械机构的使用体验[6,7]。
1 机械结构设计
本文中涉及的上肢康复机器人的手肘部位,包括大臂关节、小臂关节、驱动电机、减速齿轮箱及柔性齿轮单元,如图1所示。
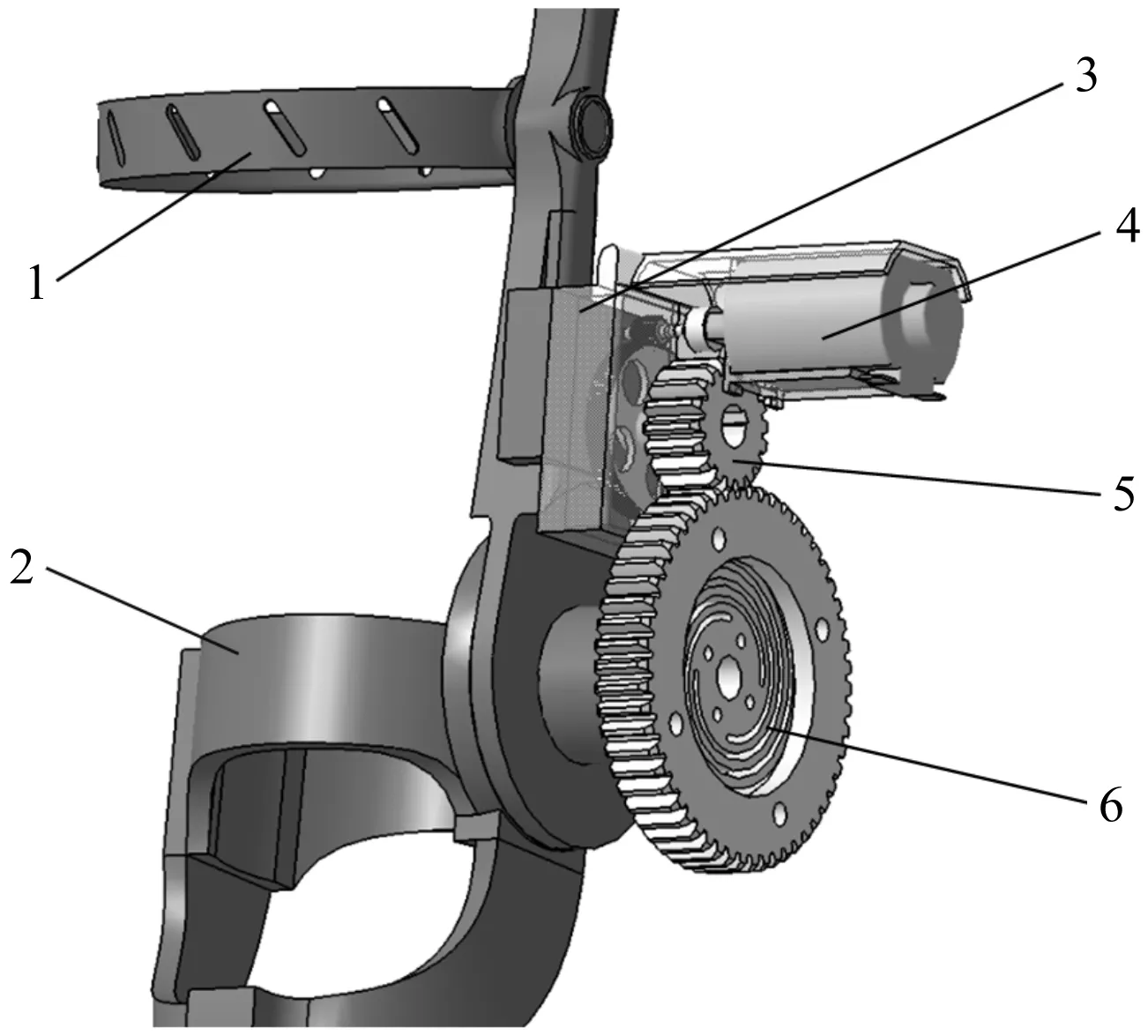
图1 康复机器人肘部关节结构1—大臂支撑;2—小臂支撑;3—减速齿轮箱;4—直流电机;5—小齿轮;6—柔性齿轮单元
根据肌体运动原理,康复机器人在做康复训练时,肘关节由屈到伸动作开始的瞬间,由支撑肘关节的柔性关节主动实施柔性驱动;肘关节由屈到伸动作结束的瞬间,柔性关节被动吸收机械手臂的动能。柔性关节不仅在患者使用康复机器人做康复运动时,对其手臂起到缓冲、减震作用,还可以发挥柔性单元的能量储存、释放作用,避免患者与康复机器人之间运动不同步的问题,提高使用安全性。
其中,扭矩齿轮单元的结构组成如图2所示。

图2 柔性单元齿轮单元1—环形齿轮;2—螺钉;3—四节点柔性单元
1.1 四节点柔性单元的设计
柔性单元的具体设计3D图,如图3所示。
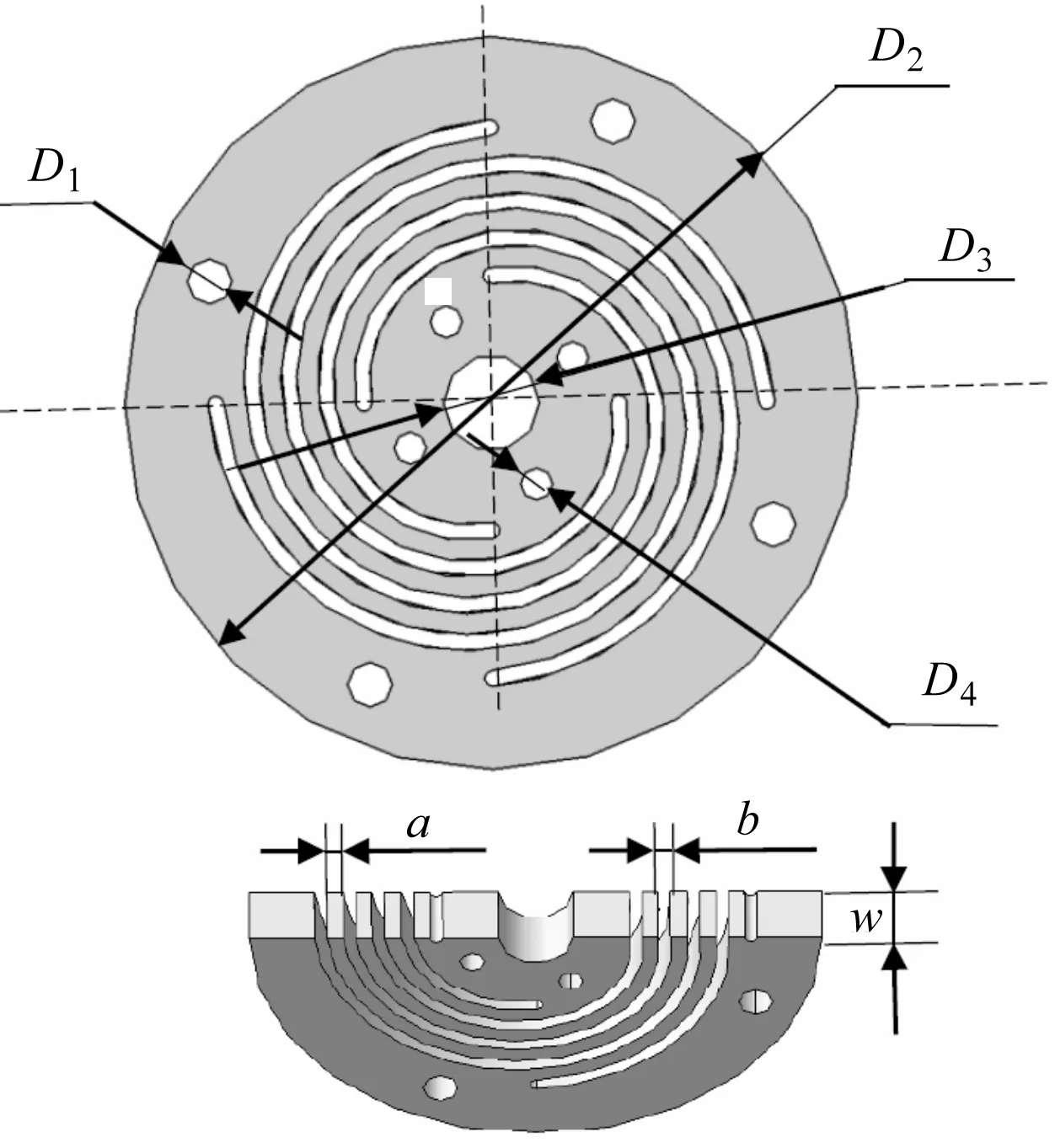
图3 柔性单元的三维图
柔性单元的参数表格,如表1所示。

表1 柔性单元参数
2 柔性单元的动量分析
根据图4分析可知该机构的运动方程:
当该机构在自由状态下,前端手臂重心到扭转弹簧中心长度为L,水平方向的夹角为0°,如图4(1)所示。当前臂加载时,其水平方向的夹角为θ1,手臂质量为m1,前臂机械结构的质量为m2,如图4(2)所示。当电机施加扭矩M时,前臂与水平的夹角为θ2,如图4(3)所示。
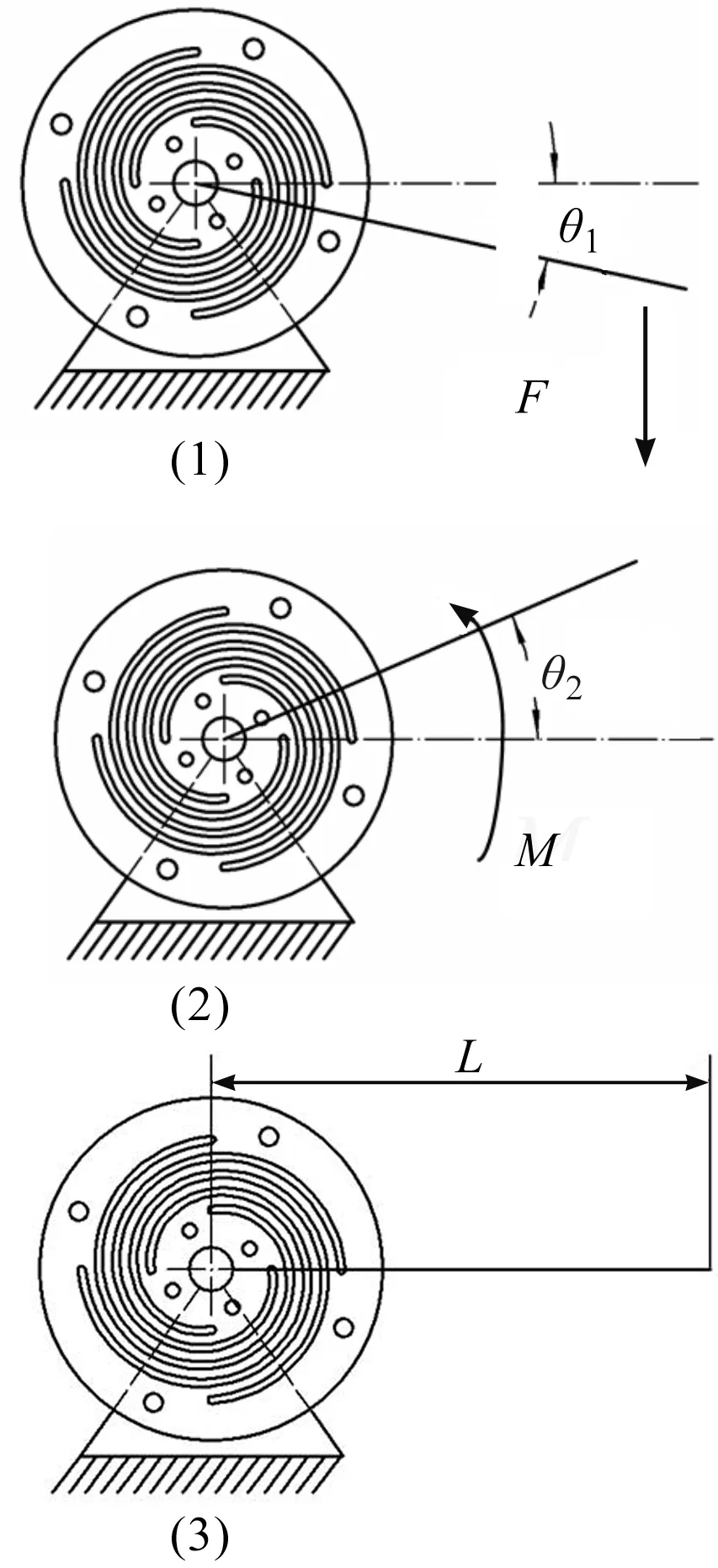
图4 柔性单元的各阶段状态
弹簧的刚度k,如下式所示:
(1)
式中:E—材料的弹性模量;K—系数。
外端固定时,K=1;内端固定时,K=2。计算得出该柔性单元的k为24 027 840 N/m,该机构的势能可由式2表达为:
(2)
其中:θ3=θ1+θ2;m3=m1+m2。
该机构动能的表达式为:
(3)
拉格朗日方程定义为:
(4)
该装置的动力学方程可以表达为:
(5)
与式(4,5)联立得到:
(6)

(7)
该机构在平衡位置,输入的扭矩可表达为:
M=m3gLcosθ3
(8)
所以机构的动态方程可表达为:
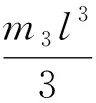
(9)
下文将应用该动力学模型来进行分析和试验。
3 柔性单元的有限元分析
3.1 有限元分析前处理
模拟实验通过ANSYS 19.1R进行,次柔性单元的边界条件设为外端固定,以内端施加扭矩[8]。本文中所用的材料为7075铝,其材料特性如表2所示。

表2 材料特性表
3.2 有限元后处理
笔者通过Workbench来验证柔性单元的机械性能。该柔性单元的有限元分析结果如图5所示。

图5 柔性单元有限元分析
笔者通过多次对模型进行模拟,并收集和绘制扭矩与其他变量之间的关系。通过施加最大4 N·m的扭矩时,产生最大的应力为440 MPa,而该材料的屈服应力为1 176 MPa,该柔性单元的安全系数为2.94,满足设计要求。其最大的变形量为3.192 mm,并且可以在扭矩与应力与变形之间呈线性关系,具体关系如图6所示。
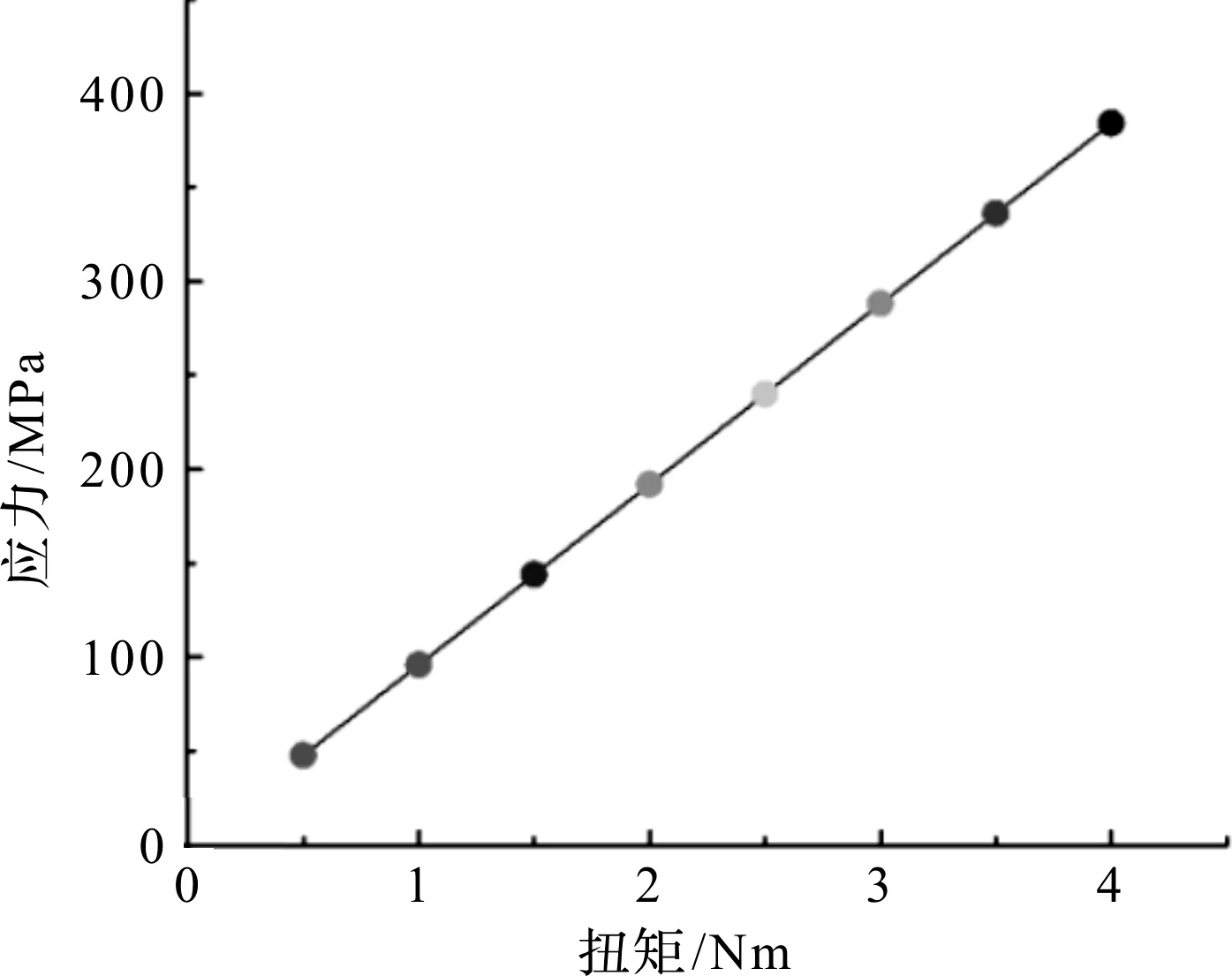
图6 扭矩与应力之间的关系
该柔性单元的应变能量最大为0.254 MJ,应变量与扭矩的关系不是线性关系,扭矩与应变能量之间的关系如图7所示。

图7 扭矩与应变能量之间的关系
对疲劳寿命进行分析流程,该柔性单元的疲劳寿命云图如图8所示。

图8 柔性单元疲劳寿命分布图
使用材料7075铝制作的柔性单元最小使用寿命为2.578×105次,康复机器人的康复循环运动周期为10 s/次。由此可以计算出次柔性单元的最小使用寿命为716.1 h。并且可以通过疲劳寿命云图看出发生疲劳相对薄弱的地方,说明该静力学分析对疲劳寿命有一定的参考意义。
4 试验平台搭建及验证
为了获取柔性单元的材料力学参数,通过搭建试验工装对本柔性单元进行试验,如图9所示。
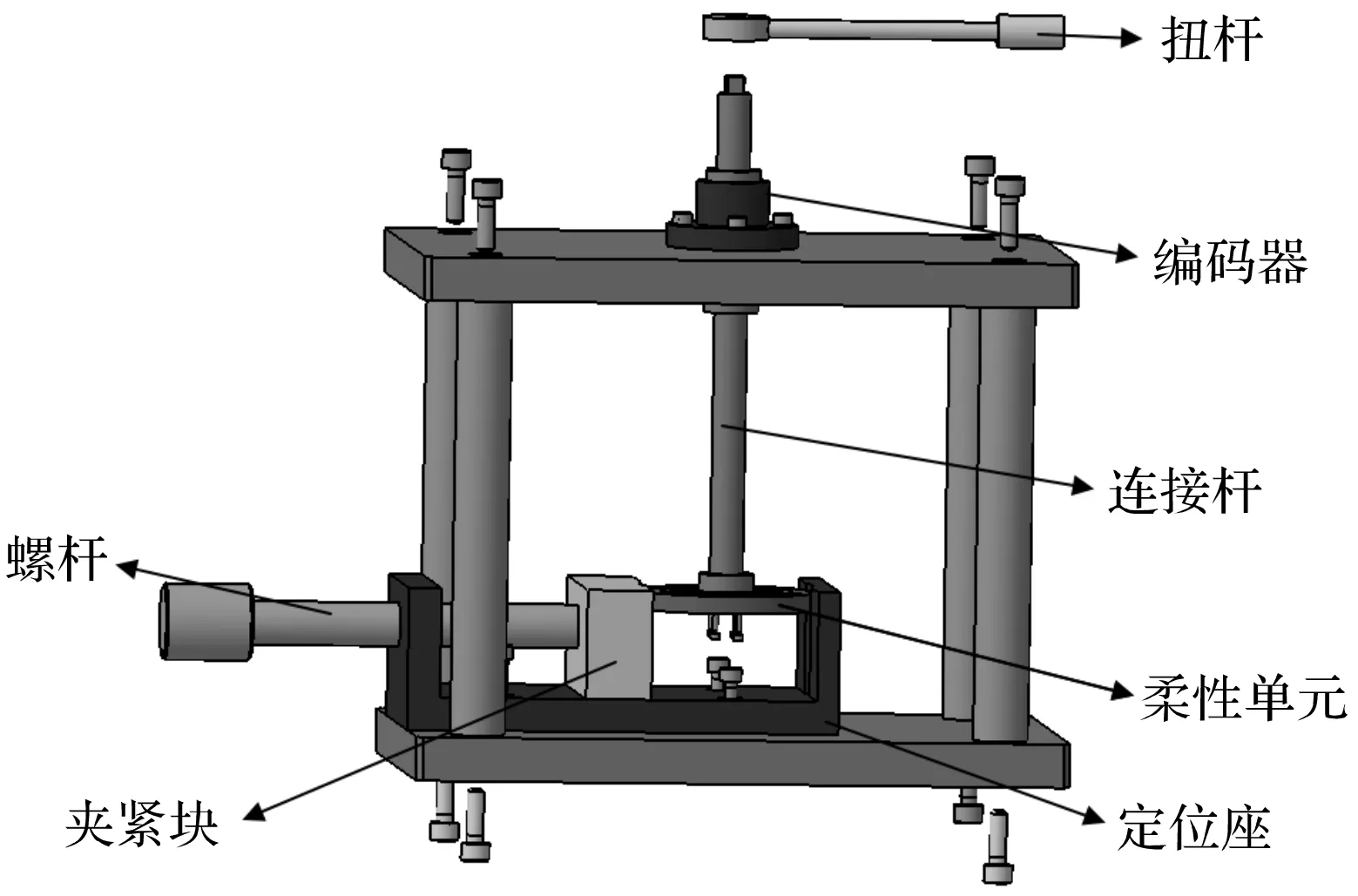
图9 柔性单元实验工装
通过扭矩扳手对柔性单元进行测试,并通过编码器对扭转角度进行记录,环境温度25 ℃[9-11]。试验原材料和试验现场如图10所示。

图10 实验过程
绘制仿真数据、实验数据与扭转角度之间的关系,如图11所示。
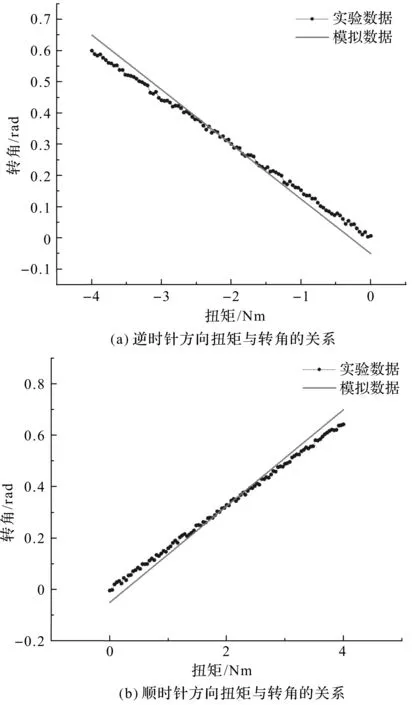
图11 柔性单元扭矩与转角之间的关系
该柔性单元在逆时针方向,实测柔性单元的的刚度为7.23 N·m/rad,模拟的刚度值为6.65 N·m/rad。在顺时针方向,实测柔性单元的的刚度为6.29 N·m/rad。模拟的刚度值为5.78 N·m/rad,模拟数据与试验数据之间的差为:
Err=(Ke-Ks)/Ks×100%
(10)
逆时针方向的刚度误差为8.7%,顺时针方向的刚度误差为8.8%。从所得数据可知:由于柔性单元顺向和逆向材料屈服方式不同,刚度也存在一定的差异。
5 结束语
本文设计了一种新型四节点柔性单元结构,三维建模后通过拉格朗日方程推导出此结构的动力学方程,利用ANSYS有限元分析软件对该柔性单元的应力、形变和应变能量进行分析。
分析结果表明:在施加最大扭矩4 N·m的情况下,此柔性单元的最大应力为440 MPa,最大变形量为3.19 mm。
通过实验验证,可以得出:此柔性单元的应力和变形量与扭矩呈线性关系,最大的应变能量为0.546 MJ,其中与扭矩呈非线性关系,且安全系数为2.94,最小使用寿命为716.1 h;该柔性单元重量轻、柔韧性高,可以较完美地解决人机交互中的部分安全问题。
