康普顿相机成像技术进展

武传鹏李 亮

1（清华大学工程物理系 北京100084）

2（粒子技术与辐射成像教育部重点实验室（清华大学）北京100084）

康普顿相机是一种无需使用机械准直的新型γ 射线成像模式，它基于康普顿散射的原理进行三维空间内射线的定位和成像。本文综述了康普顿相机的发展历史，以及近年在各个应用领域的最新研究进展，并重点关注了康普顿相机在医学成像和环境辐射监测领域的学术前沿课题。本文第一节对康普顿相机的基本情况进行了简介，简述了其工作机理及在多种领域中的应用，并对其主要的结构演变历程进行了梳理；文章第二节主要对康普顿相机的成像物理基础、原理以及相关重建算法进行了详细描述；第三节主要叙述了康普顿相机的几种性能指标及其影响因素；第四节主要介绍了几种康普顿相机的最新型系统结构，并对该领域的最新研究成果进行了汇总和对比介绍。

1 康普顿相机技术介绍

γ光子有着穿透性好、可以携带物质信息的优良特性，然而它无法被轻易聚焦，这给使用γ射线成像带来了困难。获取γ光子方向信息的最常见方式是使用准直器，如使用机械准直的Anger相机结构［1−2］、编码孔成像技术［3］等。然而，在使用机械准直结构的成像模式中，如单光子发射计算机断层成像技术（Single Photon Emission Computed Tomography，SPECT）［4］等，不得不在探测效率（灵敏度）与空间分辨率之间做取舍：为了取得更高的空间分辨率，必须要采用较小的准直孔径，这却使得通过小孔被收集的光子变少，探测效率变低［5］。

康普顿相机是一种非机械准直的新型成像模式，有着独特的成像模式和成像优势。它借由康普顿散射的物理效应追踪入射光子来向，即进行“电子准直”。在医学成像领域，康普顿相机克服了SPECT等核医学系统由于机械准直而带来的弊端，有着更高的探测效率；而在环境辐射监测领域，康普顿相机与传统的编码板对比，前者的成像视野更宽广，此外后者还有着成像能区的限制，当射线能量过高时可能穿透编码板带来图像噪声。综合以上因素，康普顿相机在大视野、宽视场、高分辨、高探测效率的成像任务中有着很大的发展潜力。康普顿相机的概念最早在天文观测领域提出，1973年Schonfelder等［6］制成了观测1～10 MeVγ射线源的天文学观测仪器。1991年，美国国家航空航天局（National Aeronautics and Space Administration，NASA）［7］研制的康普顿γ射 线 天 文 台（Compton Gamma Ray Observatory，CGRO）卫星上也使用了名为CMOPTEL的康普顿相机系统。随着康普顿相机技术的发展，它被迁移到许多其他应用领域，这主要包括两类任务：局部视野成像，如医学成像、质子治疗等医学应用；开放式视野成像，如环境辐射监测、三维辐射场研究等。

医学成像领域的应用是人们最为关注的。1974年Todd等［8］最早将康普顿相机的概念引入医学成像。1977年Everett等［9］验证了康普顿相机应用在SPECT上的可行性，并进行了仿真实验。Singh等［10−11］在1983年制成了放射性同位素示踪的医学康普顿相机的原型机，并进行了实验结果的展示和分析。近些年，康普顿相机在医学成像领域有了更多的应用和研究进展，比如放射性示踪成像、癌症诊断、手术引导、X射线荧光成像等。日本群马大学使用Si/CdTe康普顿相机对99Tcm和18F等放射性药物进行成像，通过仿真实验和模体实验验证了系统可行性，并在小鼠体内成功实现了示踪剂活体成像，还成功进行了临床实验。其最佳成像角分辨率可达到4.9°（511 keV）［12−18］。手术引导方面，康普顿相机也可在腹腔手术中作为腹腔镜照相机，以进行手术引导［19−20］。2016年Vernekohl等［21−22］通过蒙特卡罗仿真，验证了康普顿相机用于X射线荧光成像的临床可行性。从这些研究中可以看到，康普顿相机成像的空间分辨率与传统核医学的SPECT等相当，且能够使用多种放射性示踪剂同时成像，由于有效探测面积更大，在探测效率上更具有优势。

在环境辐射监测领域，Sinclair与Herbach［23−24］于2009年先后针对放射性危险物质监测进行了仿真实验，并在结果上取得了一致性。2013年，Kataoka等［25］提出了一种基于三维位置敏感闪烁体和薄单片多像素光子计数器（Multi-Pixel Photon Counter，MPPC）阵列的手持康普顿相机，其用于环境辐射监测时，对662 keV光子的角分辨率可达到14°。同年，Kong等［26］提出了用于远程辐射源定位和识别的康普顿相机阵列原型，该相机由大体积闪烁体探测器制成，这为散射光子提供了大视野，并以适中的成本实现了最大的效率。该技术还被用于核电站辐射检测，如福岛核电站事故核泄漏的放射性监测［27］；2014年，Kishimoto等［28］提出了一种将三维位置敏感闪烁体耦合到多像素光子计数器阵列上的手持康普顿相机，其灵敏度比同类用于福岛检测的相机高几倍；2015年Takeda等［29］提出了一种基于Si/CdTe的便携式康普顿相机用于福岛检测；2016年Jiang等［30］在福岛的最新相关研究已经对137Cs和134Cs实现了1.68%的探测效率和约14°的角分辨率。密歇根大学He课题组［31］使用三维位置灵敏大体积碲锌镉探测器，制成的康普顿相机也在环境辐射检测上取得了不俗的成绩。

近十年，粒子治疗（如质子治疗）成了医学领域一个炙手可热的话题，相比于X射线放疗，其瞬发γ光子能量沉积更具选择性，因此可以更有针对性地杀伤肿瘤细胞，减少对正常组织的损害［32］。影响瞬发光子的产生与分布的一个重要因素就是吸收剂量［33］，因此粒子治疗的剂量监测成为了热门话题，许多类型的检测设备正在被研究以进行瞬发光子的剂量监测［34−36］。其中，康普顿相机也表现出了很好的潜力，近年来涌现了一大批使用康普顿相机进行瞬发光子剂量监测的研究［36−41］。

被应用于如此多的领域，可见康普顿相机有着独特的成像优势，是一种被人们所关注的成像模式。随着大量针对康普顿相机的研究，其系统结构也不断被优化和革新。

随着电子学技术和探测器技术的发展，不断有各种新型康普顿相机被提出，康普顿相机的成像系统结构经历了以下几个阶段的演进：1）双层闪烁体探测器结构；2）双层半导体探测器结构，包含了双面条形型探测器和像素阵列型探测器两种获取二维位置信息的方式；3）新型结构康普顿相机，包含“分离式”结构和“一体式”结构。主流康普顿相机系统结构的演进情况如图1所示。

图1 康普顿相机系统结构的演进过程Fig.1 The evolution of system structure of Compton camera

最早的康普顿相机主要是使用闪烁体探测器的双层探测器结构。比如前文提到的，最早由Schonfelder等［6］制 作 的 天 文 学 康 普 顿 成 像 仪、NASA［7］的CMOPTEL康 普 顿相机、Singh等［10］在1983年制成的首台医学成像康普顿相机的原型机都是如此。

随着探测器技术发展，半导体探测器由于其探测效率高、能量分辨率好、线性好、时间响应快等优良特性，开始成为康普顿相机系统中探测器的主流。为了获得康普顿散射发生的位置信息，探测器主要使用了双面条形型探测器和像素阵列型探测器两种类型。1988年Kamae等［42］设计的硅微条探测器+闪烁体的双层结构，1996年Phlips等［43］两层的双面条形高纯锗探测器的双层结构等。2010年伯克利大学的Chivers等［44］还提出了使用硅基CCD+双面条形高纯锗的双层结构，该系统的优点是可以得到反冲电子轨迹，位置信息更加精确。渐渐地，双面条形半导体探测器不再能满足人们在空间分辨率上的需求，像素阵列探测器开始逐步取代条形探测器。1998年LeBlanc等［45］采取了像素阵列硅探测器制作康普顿相机用于核医学成像，并得到了优于传统SPECT的成像效果。2016年Vernekohl等［21−22］通过蒙特卡罗仿真Si/CdTe双层探测器结构，验证了康普顿相机用于X射线荧光成像的临床可行性。

除了传统的双层半导体探测器结构，近年人们又以此为基础，探索了多种新型结构的康普顿相机，比如“分离式”的多层探测器结构、“一体式”的单层探测器结构等。这些最新前沿进展将在第四节进行重点叙述。

近年来，国内几家单位也针对康普顿相机展开了一系列的探索和实验研究。2016年，中国工程物理研究院的丁长骥等［46−47］开展了Si/CZT双层像素探测器结构的蒙特卡罗仿真，对137Cs（662 keV）成像的角分辨率为7.3°，成像效率为0.15%。同单位的张迎增等［48−49］于2019年对康普顿相机的性能指标及影响因素进行了分析，并仿真了DSSD+NaI双层闪烁体探测器康普顿相机应用于Steve Fetter核弹头成像的性能。清华大学刘益林等［50］于2018年使用三维位置灵敏CZT探测器，搭建了真实的康普顿相机系统，对137Cs（662 keV）成像的角分辨率为9.6°。2019年，中国科学院的宋张勇等［51］对康普顿相机的分辨能力进行了分析，并进行了GENT4仿真和反投影算法重建。中国原子能科学研究院的王薇等［52］于同年对影响角分辨率的主要因素进行了定量的理论推导和计算。

2 康普顿相机成像原理及重建算法

2.1 康普顿相机成像的物理基础

众所周知，γ射线和X射线在于物质发生相互作用时，有三种主要的物理机制：光电效应、康普顿散射效应、电子对效应［53］。其中，在发生康普顿散射效应时，入射光子与原子核外的外层电子发生碰撞，电子获得入射光子的一部分能量成为反冲电子，而入射光子损失能量并发生方向偏转，偏转角度θ一般被称为散射角，反应过程如图2所示。

发生康普顿散射后，散射光子的能量与散射角θ有关，关系如式（1）所示：

式中：E0和Ec为入射光子和散射光子能量；θ为康普顿散射角；me为电子的静止质量，mec2=511keV。

图2 康普顿散射效应示意图Fig.2 Schematic diagram of Compton scattering effect

当有大量光子入射，康普顿散射反应后，散射光子出射到不同角度θ上的概率并不一致，康普顿散射截面服从克莱因-仁科（Klein-Nishina）公式分布，简称KN公式［54−55］，如式（2）。而散射角相同的散射光子，在围绕入射方向的立体角分布上是均匀分布的。

式中：fKN(E0，θ)为入射光子能量为E0、散射角度为θ时的康普顿散射微分反应截面；dσ为康普顿散射后，散射角在θ方向上dθ内的概率；re为经典电子半径，re=e2mec2=2.818×10−13cm；α=E0mec2。康普顿散射的微分截面分布示意图如图3所示。

图3 康普顿散射微分截面随散射角变化的分布图Fig.3 The distribution of Compton scattering differential cross section with scattering angle

然而通常情况下，初始原子核外电子并不是处于静止状态的，而是被束缚在原子核外轨道上，并且处于运动状态中，因此即使入射光子是具有完全相同方向和能量的，散射光子的出射方向和能量大小也并不完全一致，而是存在一定的不确定度。该不确定度被称为多普勒展宽，这一现象被称作多普勒展宽效应［57］。

以上就是康普顿散射效应的基本物理原理，通过式（1）可以发现，当我们探测到入射光子能量和散射光子能量时，我们便可以得到散射角θ的大小，如式（3）。进而可以确定发生康普顿散射的入射光子源的空间位置所在的方向，这便是康普顿相机成像的物理基础。

2.2 康普顿相机的成像原理

典型的康普顿相机系统由双层探测器结构组成，如图4所示。入射光子在第一层探测器上发生康普顿散射，探测器记录反应发生的位置R1（x1，y1，z1）和沉积的能量E1；散射后的散射光子射出第一层探测器，在第二层探测器上R2（x2，y2，z2）位置被完全吸收，沉积能量E2。入射光子的能量即为两次沉积的能量之和，即E0=E1+E2。因此，只需将E0和E2代入式（3），便得到了康普顿散射的散射角θ。由于不知道入射光子来向的具体方位角，但是我们能确定的是，其方向在以R1、R2为轴夹角为θ的圆锥面上。当我们探测到足够多的康普顿散射事件，每一个事件都可以反算出一个对应的圆锥面，这些圆锥面交汇所得理论上便是放射源所处的空间位置。

由于我们希望在第一层探测器中尽可能多地发生康普顿散射事件，因此通常采用低Z材料的探测器，如硅半导体探测器；而第二层探测器中，我们希望射线更多地沉积能量，以使散射光子完全被吸收，因此常用的材料如CdTe探测器、CZT探测器、高纯锗探测器等。当然并非局限于此，近年来许多其它类型的探测器搭配同样可以得到不错的成像结果。

图4 典型康普顿相机成像原理示意图Fig.4 Schematic diagram of imaging principle of typical Compton camera

2.3 康普顿相机的图像重建算法

康普顿相机的重建算法主要分为解析算法和迭代算法两大类。

解析重建算法中，最常用的是直接反投影算法和滤波反投影算法［57］。直接反投影算法的思路非常直接，通过遍历整个像素空间，看每个像素点是否在事件所反算的圆锥面上，如果在则按权重在该点处叠加一个值，当所有事件均完成反投影，即可重建出放射源所在的空间位置。这种算法存在的问题是没有放射源的位置也难以避免地被赋值，因此哪怕在理想条件下，图像依然会有伪影存在，Basko等［58］在1998年提出了一种基于球谐函数的滤波反投影算法，以消除这些反投影算法带来的伪影。

由于康普顿相机系统的一些固有特性，由解析算法重建得到的图像，是真实图像的有偏估计，而迭代算法可以得到真实图像的无偏估计，且可以引入噪声模型。迭代重建算法的思想是，将重建问题建模成数学问题，通过解方程组g=Hf来得到重建图像，其中：g为探测器响应；H为系统矩阵；f为重建图像。

1970年Gorden等［59］提 出 了 代 数 重 建 算 法（Algebraic Reconstruction Techniques，ART）算法，其思想是用当前图像的前向投影与真实投影之间的偏差反向修正重建图像，经过多轮迭代至收敛，其迭代过程如式（4）。该算法还被进一步改进出联合代数重建算法（Simultaneous Algebraic Reconstruction Technique，SART）、乘 法 代 数 重 建 算 法（Multiplicative Algebraic Reconstruction Technique，MART）、约束乘法代数重建算法（Constrained Multiplicative Algebraic Reconstruction Technique，CMART）等算法［60−61］。

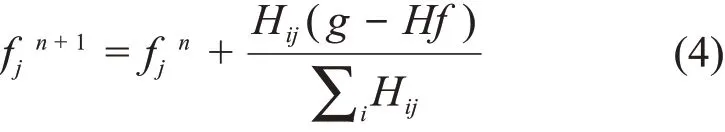
另一类迭代算法是最大似然法（Maximum Likelihood，ML）［62］，其主要思想是寻找使投影（探测器响应）出现的概率最大的重建图像，引入泊松噪声后，其形式如式（5）。为了更好地求解该概率公式，1982年Shepp等［63］提 出 了EM（Expectation Maximization）算法，以克服求导运算的不便。MLEM算法很好地保持了图像的非负性，且每次迭代后，源强度总和恒定。

近年来，为优化传统重建算法中存在的噪声、准确性、运行速度等方面的问题，一系列的新型重建算法被提出。解析重建算法方面，基于Radon变换的滤波反投影算法被提出，以解决简单反投影算法噪声严重、成像分辨率差的问题。迭代重建方面，对MLEM算法改进的LM-MLEM算法被提出，该算法基于列表模式的权重法，带来了更精确的结果。此外，由于MLEM及其衍生算法均基于像素驱动，在高分辨率、大视野任务中，计算复杂度高、速度慢，基于事件驱动的随机起源算法（Stochastic Origin Ensemble，SOE）被提出，该算法复杂度更低，运行更快。

3 康普顿相机成像性能指标

3.1 主要成像性能指标

评价一个康普顿相机系统所使用的主要性能指标有：点源位置精度［64］、点源空间分辨率、探测效率、角分辨率（Angle Resolution Measurement，ARM）［65］。其中人们较少关注电源位置精度，更加关注后三种评价指标，而角分辨率是最重要的指标［49−50］。

点源位置精度只使用康普顿相机对点源重建时，图像分布上点源中心点（即密度数值最大的点）与点源真实中心点之间的接近程度。

点源空间分辨率是重建图像上能够识别两个相邻目标的最小距离，该指标表征了空间细节分辨能力。通常我们从重建结果图像上计算该指标，具体方法是将点源重建的图像做分布图，找到凸起峰并获取最高点计数，在该最大值二分之一处圆面的直径记作峰半高宽（Full Width Half Maximum，FWHM），用该值表达点源空间分辨率。此外也可以从峰最大值处垂直截取平面，得到一个一维分布，拟合该一维峰的高斯分布，则FWHM=2.355σ。

探测效率，一般指康普顿成像的绝对探测效率，它通常被定义为：康普顿成像事例率占该系统探测的由放射性点源产生计数率的百分比。也即，探测效率=成像选择的事件数/探测器探测到的入射伽马光子数。

角分辨率是衡量康普顿相机性能优劣的一个最重要的指标，它被定义为反算的散射角θ（圆锥角）与真实放射源的方向之间的偏差，如图5所示。

3.2 角分辨率的主要影响因素

由于角分辨率是康普顿相机最重要的性能指标，这里单独对其影响因素进行具体分析。根据图4中的物理过程，图中θem是根据测量结果反算出的康普顿散射角。由于探测器能量分辨率的限制，因此测量到的能量含有一定误差，因此如式（6）θem包含两部分：由能量真值反算的散射角θc如式（7）和能量不确定度带来的角度误差Δθe：

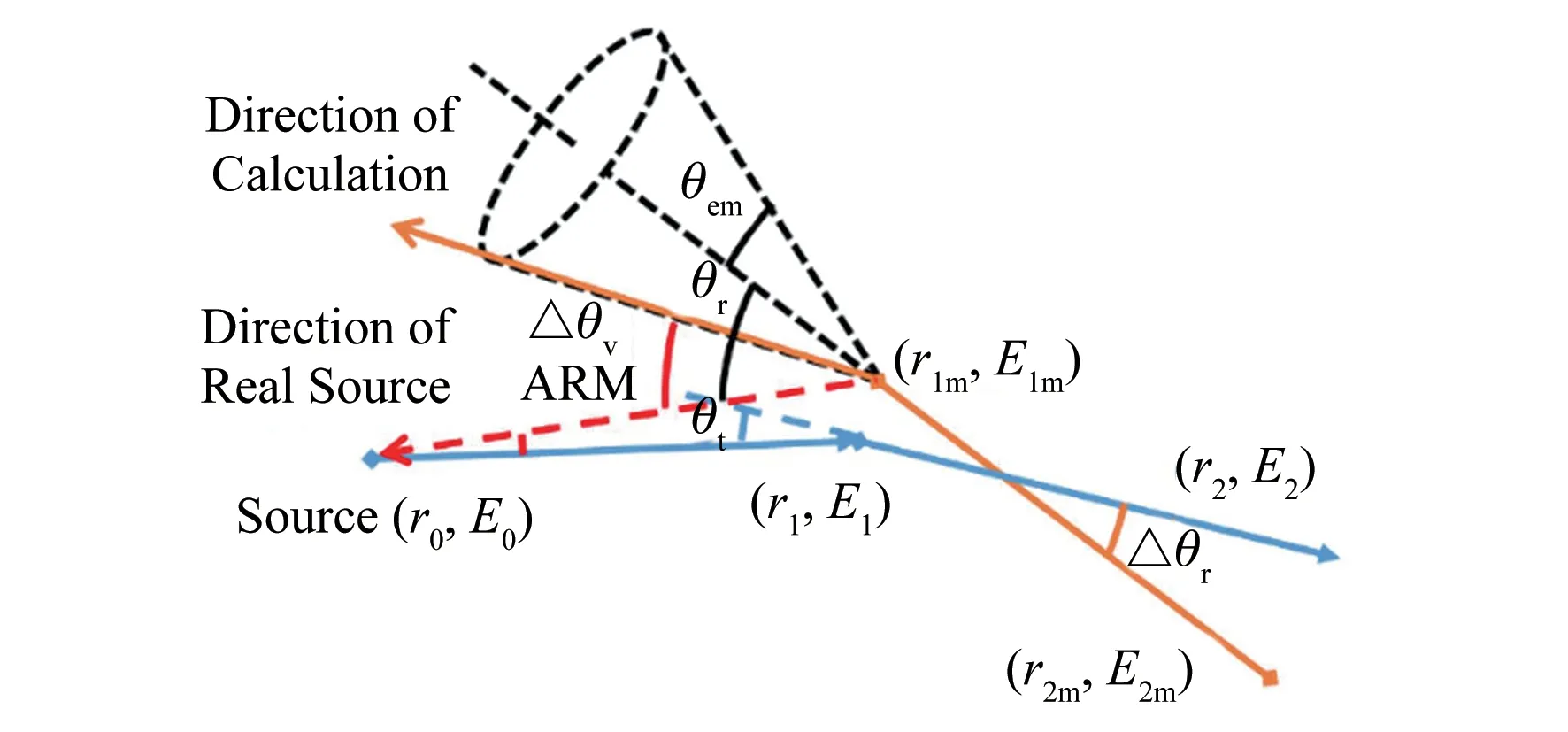
图5 角分辨率及影响因素示意图Fig.5 Schematic diagram of angle resolution and influencing factors

θt表示真实发生的康普顿散射偏转角度，考虑到多普勒展宽效应的影响带来的角度偏差ΔθD，它可以被表示为式（8）：

θr表示最终测量到的散射光的散射角，与最初真实入射的伽马光子之间的角度偏转，如式（9）。因此除了真实发生的康普顿散射偏转θt以外，该角度还受到圆锥顶点（即康普顿散射发生的位置）的不确定度Δθr影响，如式（10）：

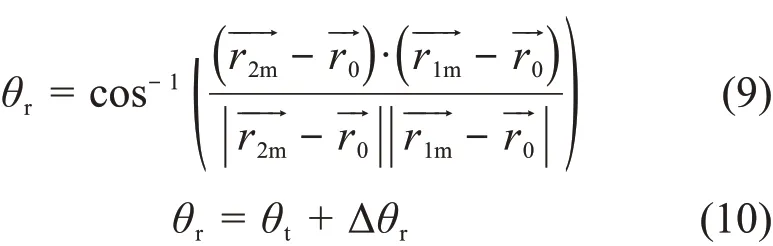
最终，我们想要得到的角分辨率，根据测量结果反算的散射角θem与真实测量的偏转角θr之间的偏差。因此综合式（6）、（8）、（10）可以计算角分辨率ARM，如式（11）：

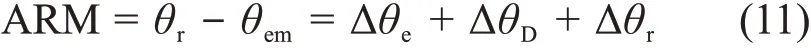
式中：Δθe是探测器能量分辨率造成的能量不确定度带来的角度偏差；ΔθD是由多普勒展宽带来的散射光子出射方向不确定度带来的角度偏差；Δθr是散射位置不准确带来的角度偏差，它与探测器的位置空间分辨率有关。

综上所述，我们可以得知，影响康普顿相机角分辨率的主要因素有三：探测器能量分辨率、探测器空间分辨率、多普勒展宽效应。除以上主要因素外，还有顶点误差、相干散射等因素会影响角分辨率，但由于在康普顿相机系统的使用场景下，这些因素的影响较小，可以忽略不计。

4 康普顿相机技术前沿进展

康普顿相机技术的发展经历了几个主要的阶段，最初人们使用两层闪烁体探测器完成康普顿成像。但随着半导体探测器技术的发展，由于其在能量分辨率、空间分辨率、探测效率以及时间响应等方面的优越性，因此双层半导体探测器结构成为了首选。需要注意的是，在散射层探测器材料的原子序数Z的选择上，既有研究采用高Z材料如高纯锗、CdTe、CZT等；也有研究选择低Z材料如硅等。两种选择各有优劣势：选用高Z材料，其探测效率更高，但多普勒展宽效应更加明显，对成像分辨率不利；而选用低Z材料，虽然康普顿截面较低，会牺牲探测效率，但康普顿散射截面占总截面的占比增高、有效事件占比更多，此外硅探测器位置灵敏度更好、多普勒展宽效应更弱，带来了更好的成像分辨率。

对于双层半导体探测器结构的康普顿相机，由于半导体探测器厚度过厚会导致z方形空间分辨率过差、制作工艺难等问题，因此直接使用双层半导体探测器结构的研究并不多。2018年Turecek等［66］基于像素阵列半导体探测器Timepix3，研发了一种由1 mm厚硅探测器和2 mm厚CdTe探测器构成的双层康普顿相机，其25 mm处的空间分辨率高达2.5 mm，是当今成像效果最理想的双层半导体探测器结构的康普顿相机之一。

随着时间的推移，近些年来，为了克服晶体较薄带来的探测效率方面的问题，人们又以双层半导体探测器结构为基础，进行了多种新型结构的探索，比如“分离式”的多层探测器结构、“一体式”的单层探测器结构等，如图6所示。

图6 “分离式”结构和“一体式”结构的康普顿相机示意图Fig.6 Schematic diagram of"separate"structure and"integrated"structure CC

所谓的“分离式”多层探测器结构并不是说单纯地增加探测器层数，而是将原本散射层、吸收层探测器分别“拆分”为多个薄探测器，完成每个康普顿散射事件探测的仍是“散射层其中一层+吸收层其中一层”的组合，所以称为“分离式”结构。2012年，Odaka和Takeda等［14］设计了一套1层0.5 mm厚硅探测器+4层0.75 mm厚CdTe探测器构成的康普顿相机，其10 cm处探测效率可达到3.4×10−6，对131I（356 keV）成像的角分辨率达到了4.5°。2017年Munos等［40］研发了一种使用LaBr3晶体的名为MACACO的三层探测器结构康普顿相机，对22Na（511 keV）实现了50 mm处低于4 mm的空间分辨率。同年，Aldawood等［67］制作了一套由6层0.5 mm厚硅双面微条探测器+1层30 mm厚LaBr3探测器的康普顿相机，对137Cs（662 keV）成像在50 mm处空间分辨率为4.8 mm。这类“分离式”结构因层数增多，因此位置分辨率更好、多普勒展宽较小、空间分辨率更好；但探测器厚度依然很薄，因此探测效率和成像视野依然会有所牺牲。

另一类新型结构是“一体式”的康普顿相机结构，其主要思想是使用单层探测器，并通过其他手段获取探测器中能量沉积位置的深度信息，以完成重建。2002年，Wulf等［68−69］提出了一种单层双面条形硅探测器结构，通过将阴阳两极的触发时间差转化成为z方向的值来获取深度信息。密歇根大学的He课题组［70］提出了独特的三维位置灵敏CZT半导体探测器，该探测器有着晶体内沉积位置三维坐标探测、晶体体积大、探测效率高、能量分辨率高、空间分辨率好、常温工作等优良特性。他们使用的15 mm厚大体积CZT晶体探测器，其最佳工作性能下对137Cs（662 keV）射线探测的能量分辨率高达0.35%，三维空间分辨率高达0.3 mm，用其制成单层探测器“一体式”康普顿相机对137Cs（662 keV）成像角分辨率约为5°［71］。2018年，Liu等［50，72］使用同样的三维位置灵敏CZT探测器，其康普顿相机系统对137Cs（662 keV）成像的角分辨率为9.6°，成像效率约为2%。2020年，Turecek等［73］基于光子计数探测器Timepix3，提出了一种只使用一层CdTe探测器的康普顿相机结构，该系统借由该探测器的1.6 ns高时间分辨率特性，由电荷漂移时间来转化得到深度信息，最终得到了几度的角分辨率。

该类“一体式”结构的优点是：晶体更大探测效率高，能量分辨率、空间分辨率都更好，有着全空间的成像视野，单晶体使得相机整体结构更小，容易制成便携式设备。然而缺点也很明显：在单一晶体内，无法直观判断出粒子沉积能量的顺序，因此很难分辨入射光子沉积与次级的散射光子沉积，需要使用事件序列重建方法，给重建过程带来了很大困难；且电子学读出电路更复杂；此外探测器成本较高。表1展示了近年来世界上成像效果较为理想的一系列康普顿相机系统，并汇总了它们所用系统结构以及成像性能等信息。

表1 先进康普顿相机系统汇总Table 1 Summary of state-of-the-art Compton camera systems

5 结语

对于康普顿相机，在进行系统结构设计时，需要注意以下几方面问题。在探测器方面：闪烁体探测器由于性能上的劣势，现今已经很少使用于康普顿相机领域；而半导体探测器由于其探测效率高、能量分辨率好、线性好、时间响应快等优良特性，使用更为广泛，其中阵列像素半导体探测器逐步取代双面条形半导体探测器成为主流。而在半导体探测器的材料原子序数选择上：高Z材料探测效率更高，但多普勒展宽效应更加明显，成像分辨率低；低Z材料探测效率上有所牺牲，但位置灵敏度更好、多普勒展宽效应更弱，带来了更好的成像分辨率。在康普相机的系统结构方面，双层半导体探测器结构以及其改进结构仍然是主流，但也有新型结构出现：“分离式”多层探测器结构牺牲了部分探测效率和成像视野，但成像分辨率更高；“一体式”结构探测器能量分辨率、空间分辨率好，探测效率和成像视野也更大，但重建算法、电子学读出都更复杂，探测器成本较高。通过调研和对比，世界上最先进的康普顿相机系统，其最好的成像角分辨率普遍已可达到几度量级，成像的空间分辨率已普遍达到mm量级。结合其在探测效率、放射性药物性能等方面的优势，我们认为对于医学放射性示踪剂的分子功能成像，康普顿相机是一种很有发展潜力的成像模式。