1.3 GHz连续波超导射频腔的数字低电平系统和模拟腔研究

刘 奎 顾 强 张俊强 赵明华

1（中国科学院上海应用物理研究所 上海201800）

2（中国科学院大学 北京100049）

3（中国科学院上海高等研究院 上海201204）

上海高重复频率硬X射线自由电子激光（Shanghai HIgh-repetition-rate X-ray free-electron laser aNd Extreme light facility，SHINE）的重复频率为1 MHz，并由1.3 GHz连续波超导直线加速器驱动［1‒2］。对于1.3 GHz连续波工作的超导射频腔，高负载品质因数（～107）会导致腔体在电磁频域上有极窄的带宽，导致射频（Radio Frequency，RF）谐振腔有相对较小的失谐就会引起腔场的幅度和相位发生较大变化。

此外，谐振腔的电磁模式和机械模式的相互作用，也会影响腔场的稳定。洛伦兹力失谐（Lorentz Force Detuning，LFD）就是由强电磁场和腔壁电流引起的腔体几何形状的变形。LFD具有多种机械特性，并耦合了外部机械噪声。时域动态LFD的二阶模型为［3］：

式中：Δωk(t)是由机械模式k贡献的电磁频率偏移；τk是每种模式的阻尼时间常数；Ωk是机械模式k的固 有频 率；Kk是 洛伦 兹力 系数；Kk0·V0是 稳 态 的LFD；ΔV(t)是腔场电压的变化。

在超导腔老练或重启过程中，逐渐上升的腔场的梯度会导致LFD的增加，继而造成发生器驱动（Generator Driven Resonator，GDR）低电平（Low Level RF，LLRF）系统出现“ponderomotive”不稳定性，甚至崩溃［3‒4］。

本文基于System Generator［5］开发了工作在腔体超导腔老练或重启过程中的自激励环路（Self-Excited Loop，SEL）低电平控制系统，以避免控制系统发生崩溃［6］。SEL系统中包含两种工作模式：free SEL模式和locked SEL模式。free SEL模式可以在腔体失谐时跟随腔体的谐振频率，保证腔场幅度的稳定［6］。locked SEL模式能在腔体有较小失谐时保证腔场幅度和相位的稳定，也可以用作补偿麦克风噪声的影响［7‒8］。GDR控制系统也包含在控制系统中，用于腔体谐振情况下保证腔场幅度相位的稳定。此外，本文所采用的1.3 GHz连续波超导RF腔高频参数如表1所示，它的数字模拟腔也被开发并在硬件上实现。基于微型计算机架构（Micro Telecommunications Computing Architecture，MicroTCA.4）平台的测试结果显示：在腔体失谐情况下，free SEL低电平系统仍能保持腔场幅度的稳定性；locked SEL既能保证腔场幅度的稳定，也能保证腔场相位的稳定。

表1 1.3 GHz连续波超导腔高频参数Table 1 Parameters of the 1.3 GHz continuous-wave superconducting RF cavity

1 低电平控制系统设计

1.3 GHz射频腔的电磁频段很高，因此它很难被模数转换器（Analog-to-Digital Converter，ADC）直接采样。在低电平系统中，模拟前端采用了下变频技术，该技术将RF信号与本地振荡器信号（Local Oscillator，LO）混合，然后使用模拟低通滤波器去除高频部分，获得中频（Intermediate Frequency，IF）信号。本地振荡器发生器模块（Local Oscillator Generator Module，LOGM）接收来自主振荡器的1 300 MHz RF信号输入，并提供1 300 MHz参考信号（Reference，REF），1354 MHz本 振（Local Oscillator，LO）信 号，81.25 MHz时 钟 至 基 于MicroTCA构 架 的mRTM（Micro Rear Transition Module）低电平控制后插板卡，以及AMC（Advanced Mezzanine Cards）低电平主控制板卡。mRTM低电平后插卡主要用作AMC低电平主控卡的模拟前端，负责RF信号的下变频和上变频。AMC低电平控制卡将通常用于包括数字信号处理部分，包括现场可编程门阵列（Field Programmable Gate Array，FPGA）主控制器、ADC、数模转换器（Digital-to-Analog Converter，DAC）和背板总线等。mRTM与AMC卡通过MicroTCA专用Zone 3连接器连接。

1.3 GHz连续波超导腔的低电平系统控制器示意图在图1中给出。在mRTM卡上，来自腔场的RF信号被下变频为IF，然后被衰减，并通过Zone 3传输到AMC卡上的ADC。同样地，在mRTM卡上也完成了上变频过程。在AMC板卡上，LLRF算法主要在FPGA上运行，non-IQ技术可以将IF解调为同相正交（In-phase/Quadrature，I/Q）信号，坐标旋转数字计 算 机（Coordinate Rotation Digital Computer，CORDIC）算法将I/Q转换为幅度和相位信号。然后，信号由SEL或GDR控制算法处理，并再由CORDIC从幅度和相位转换为I/Q。六角形方框在IQ回路中提供了一个附加的相位反馈回路，其原理如式（2）所示，该回路组成了locked SEL模式，也被称为麦克风补偿器［7］。

图1 1.3 GHz连续波超导腔的低电平系统控制器示意图Fig.1 Schematic diagram of the LLRF system for the 1.3 GHz CW superconducting RF cavity

1.3 GHz连续波超导腔的低电平系统算法结构如图2所示。控制多路选择器可以方便地将控制系统切换到GDR、free SEL和locked SEL三种模式。GDR主要用于在谐振频率与RF参考频率非常接近情况下。在GDR模式下，多路选择器Am_Sel切换到1，GDR_SEL_Sel切换到0。幅度和相位反馈环路中使用比例积分（Proportional-Integral，PI）控制器。另外，还可以调整PI控制器的参数以获得开环系统。在free SEL模式下，GDR_SEL_Sel切换到1，Ph_SEL_Sel切换到1。通过适当调整移相器，满足环路相位为的2π整数倍，环路增益大于1，则SEL环路可以获得正反馈。幅度环路可以切换到参考值Am_SP或PI反馈环路，以获得接近幅度设定点的值。在free SEL模式，即使腔体失谐许多带宽，系统也可以快速跟踪腔频率。locked SEL模式需打开Ph3回路的PI控制器，它被开发用来补偿腔体失谐的影响。值得注意的是，仅在腔振幅保持恒定的同时才能打开locked SEL模式，并且需将腔体调谐接近参考频率。在超导腔实际重启过程中，SEL与GDR系统的切换是按固定流程自动完成的。例如在美国Jefferson Lab实验室的CEBAF（Continuous Electron Beam Accelerator Facility）升级装置［9］中，超导腔的梯度从0～20 MV·m−1的过程中，使用free SEL模式去跟随腔体频率，并使腔场幅度上升到设定值。机械调谐（Mechanical Tuner，MT）系统在此期间也调谐腔体谐振频率到参考值。之后，打开GDR系统，锁定腔场到参考值位置。下面将具体介绍一下本文所采用的主要数字信号处理算法，以及在System Generator中的实现方式等。

图2 1.3 GHz连续波超导腔的低电平系统算法简图Fig.2 The diagram of the LLRF system algorithms for the 1.3 GHz CW superconducting RF cavity

1.1 Non-IQ算法

在数字低电平系统中，ADC的非线性会导致输入载波中产生高次谐波。基于IQ采样的算法简单，所消耗的资源和延时都较少，但高次谐波却依然无法滤除［10‒12］。而且，当采样频率是中频频率的4倍时，根据Nyquist采样原理，奇次谐波会叠加在中频频率上，无法通过数字滤波器滤除［13］。

为解 决此 问题，Doolittle［14］在2006年 提 出 了non-IQ解调技术，在数字低电平系统中被广泛使用。其原理是通过稍稍改变IQ解调的采样率来过滤掉大部分毗连谐波。假定n为m个RF周期的采样数，则采样率可描述为：

式中：Δφ为两个采样值之间的相位差；fclk为采样频率；fRF为RF信号频率。

Non-IQ算法的数学表达式如式（3）所示［15］，其中：yk代表IF信号的第k个ADC采样值。在实际的低电平系统中，non-IQ算法中的正余弦值存在于查找表中，根据时钟分别与ADC采样值相乘并求和，最终得到I和Q。本文中n=3、m=2，ADC采样频率为81.25 MHz。

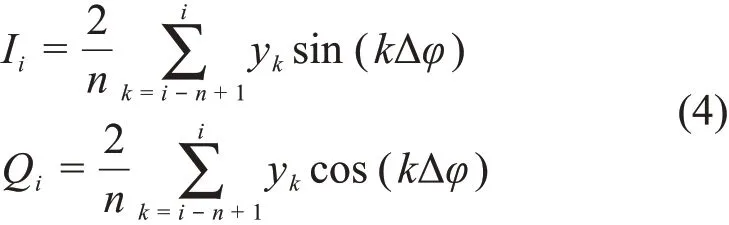
在System Generator中，内置的有限脉冲响应（Finite Impulse Response，FIR）滤波器的系数不能随时钟改变，因此本文搭建如图3所示的由延迟模块，加法器模块和一个循环计数器模块组成的一个移动平均FIR滤波器，这个滤波器能将采集的ADC样本解调成I路信号。其中，正弦值即为滤波器中的系数，它们由non-IQ算法公式计算得到。

1.2 CORDIC算法

在低电平控制系统中，CORDIC算法［16］可以快速地将IQ值与幅度相位相互转化，而且计算过程中只用了加法器，移位和少量乘法器，因此特别适合在基于FPGA中的数字低电平系统中实现。但是，转换必须快速，精确和连续，以完美实现SEL的功能［17‒18］。对于CORDIC算法的精度而言，相位误差比幅度误差更为明显，但在理论上经过18次迭代后，相位误差仍可以小于0.05%。

式中：Ki=，di=±1。由于在第一次迭代中使用20代替正切函数，CORDIC算法的旋转角度被限制在(−π/2，π/2]之间。为了满足SEL控制系统的功能，还需将IQ值的符号添加到CORDIC算法中，以将旋转角度扩展到(−π，π]之间。需要提到的一点是，由于system generator工具箱中CORDIC模块无法处理较大且快速变化的环路相位，因此本文的SEL系统表现地像相锁定环路系统。但在未来，我们将开发可以克服这一缺点的新CORDIC模块。

图3 Non-IQ算法的in-phase部分在system generator中的原理图Fig.3 Principle diagram of in-phase part of the non-IQ algorithm block in the system generator

1.3 数字PI算法

在本文的数字低电平系统中，数字PI控制器的传递函数如式（6）所示［12］，其中：Kp是比例系数；Ki是积分系数。PI控制器在system generator中实现的原理图如图4所示。为消除积分饱和的影响，重置PI控制器的参数，一个重置端口被加进了延时模块。

图4 数字PI算法在system generator中的原理图Fig.4 Principle diagram of the PI algorithm block in the system generator

2 GHz数字模拟腔

RF腔的等效LCR电路可用于研究低电平系统中RF腔的特性，基于Schilcher［19］推导出的连续时域中的RF腔基带数学模型，邱丰［20］在离散时域中建立了式（7）所示的数学模型，使得RF腔体模型能在数字硬件中实现，其中：Ts是采样时间，ω12是腔体电磁频域上的半带宽。1.3 GHz模拟腔在system generator中的模型如图5所示。

其中：

图5 1.3 GHz模拟腔在system generator中的模型Fig.5 Model diagram of the 1.3 GHz RF cavity simulator in the system generator

本文的数字模拟腔的模拟部分与低电平系统相同，因此在图6中，仅显示了1.3 GHz数字模拟腔的数字部分，除了non-IQ模块，FPGA中还包含了放大器、限幅器和腔体模型。其中，放大器只为一个简单的线性增益，在未来也可加入非线性因素，以模拟出更逼真的功率源输出；限幅器则用来模拟功率源的最大功率保护系统，以免超出功率源的正常输出范围。MicroTCA系统提供了多种用于信号传输的背板总线，数字模拟腔和低电平控制器将采用相同板卡，通过背板PCIe总线进行通信，模拟腔与低电平系统将直接插在同一MicroTCA机箱内，实现对LLRF控制系统新算法的实时测试。

图6 1.3 GHz模拟腔的布局Fig.6 The layout of the 1.3 GHz cavity simulator

3 在Micro TCA.4平台上的测试

低电平控制系统和腔体模拟器的模拟部分使用的是DWC8VM1 mRTM卡，数字部分使用的是SIS8300-L AMC板卡，如图7中所示。除此之外，整个测试平台还包含基于Micro TCA.4的基本系统，包含有背板总线和卡槽的机箱、电源模块和管理板块（MicroTCA Carrier Hub，MCH）、以及1.3 GHz信号源和LO模块。1.3 GHz信号源将产生1.3 GHz RF参考信号，通过同轴电缆输入到LO模块，为低电平和腔体模拟器提供参考和时钟信号，整个系统结构如图8所示。为了验证所设计的LLRF系统的性能，低电平系统板和RF模拟腔通过同轴电缆从后IO端口相互连接。CPU将通过背板PCIe总线读取低电平系统中和腔体模拟器中各个位置处的数据，并将其传输到CPU和SSD（Solid-State Disk），用于在上层软件中读取。

图7 mRTM板卡和AMC板卡Fig.7 Photograph of the mRTM card and AMC card

根据RF腔波特图和式（8）中所示相移，我们可以得到RF腔失谐时幅度和相移的理论值：

图8 测试平台(a)1.3 GHz RF信号发生器，(b)LO信号，参考信号和时钟发生器模块，(c)MicroTCA.4机箱Fig.8 Photographs of test platform(a)1.3 GHz RF signal generator,(b)LO signal,reference signal and clock generator module,(c)MicroTCA.4 crate

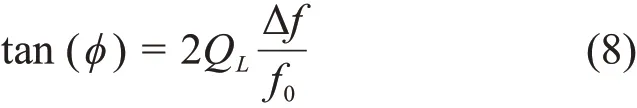
为了验证数字模拟腔，腔体的I通道被输入恒定的归一化阶跃信号，并获取Vc_I和Vc_Q的数据并将其转换为幅度和相位值。图9给出了失谐50 Hz的数字模拟腔腔场的测量值和理论值对比，理论值与测量值的幅度和相位误差分别为ΔAmVc/AmVc×100%≈0.05%和ΔPhVc≈0.003°。由于腔体数学模型在频域中的表现类似于低通滤波器，因此测量值成一条直线。

图9 1.3 GHz RF数字模拟腔失谐50 Hz时，腔场的测量值和理论值Fig.9 Comparison of the measured values and theoretical values of the 1.3 GHz RF cavity simulator under a detuning frequency of 50 Hz

在GDR模式下，GDR_SEL_Sel的选择器设置为0，而Am_Sel为1。locked SEL环路的增益必须为零。正确调整相位反馈环路和幅度反馈环路的增益后，可以轻松保持恒定的腔场。如果使模拟腔失谐较大，则控制系统将出现“ponderomotive”不稳定性。图10为仿真超导腔老练过程中，在GDR系统控制下腔体的LFD效应和腔场梯度响应曲线。在加速梯度的参考值为7 MV·m−1时，超导腔电磁模式和机械模式的相互作用使LFD出现大幅振荡，这也导致了腔场幅度出现了严重波动，发生了“ponderomotive”不稳定性。

图10 仿真超导腔老练过程中，在GDR系统控制下腔体的LFD(a)和腔场梯度响应曲线(b)Fig.10 The LFD(a)and cavity gradient response curve(b)of superconducting cavity simulator under the GDR system during the conditioning process

为了测试SEL模式，将模拟腔失谐100 Hz，将麦克风补偿器中PI的增益设置为零，将GDR_SEL_Sel设置为1，并且幅度环路可以切换到PI反馈环路。测试结果如图11所示。需要说明的是，图11和图12中的Vc-am、Vc-ph、I-out、Q-out分别对应于图2中的Am1、Ph1、Iout、Qout。测试结果表明：虽然由于system generator中内置的CORDIC模块的缺点，SEL环路的表现类似于相锁定环路系统。但是SEL环路的移相器可以抵消由失谐腔引起的环路相移，腔场的振幅是稳定的，并且不受“ponderomotive”不稳定性的影响。幅度反馈环路能将腔场幅度稳定在设定点，并且腔场幅度的稳定性为0.454 8%（RMS）。

由于在测试中很难采集到模拟腔上升曲线，为研究超导腔加载时，SEL模式切换到GDR模式对腔场的影响。本文对SEL模式到GDR模式的切换过程进行了仿真模拟，模拟结果如图12所示。在SEL模式，腔场的梯度能在20 ms内上升到15 MV·m−1。由于机械调谐系统对LFD的补偿，腔场相位会出现振荡，但振荡频率越来越小。GDR系统在50 ms时被打开，从图12中可以看出，腔场的梯度和相位能很快地被锁定到参考值。但由于麦克风噪声的影响，相位曲线还是会出现微小的波动。

当切换到locked SEL模式时，控制器输出将自动改变以补偿谐振腔失谐的影响，并能在失谐频率为5 Hz时将谐振腔的幅度和相位保持在设定点，测试结果如图13所示。腔场在幅度和相位上的稳定性分别为0.458 0%（RMS）和0.058°（RMS）。此外，本文还仿真了有其他不同恒定失谐时，locked SEL系统的入射电压幅度，反射电压幅度、腔场梯度和相位的响应曲线、仿真结果如图14所示。仿真结果表明，locked SEL系统始终可以自动稳定腔场的振幅和相位，但失谐较大时，会有较大反射电压幅度，触发联锁保护。这也说明了locked SEL模式仅适合腔体频率接近参考值时工作。

图11 在free SEL模式下，腔体失谐100 Hz时，腔场的幅度(a)、相位(b)和控制器的输出(c、d)Fig.11 Amplitude(a)and phase(b)of the cavity field,and the output(c,d)of the LLRF controller in free SEL mode under the detuning frequency of 100 Hz

图12 仿真SEL模式到GDR模式的切换过程Fig.12 Simulation of the switching process from SEL mode to GDR mode

图13 在locked SEL模式下，腔体失谐5 Hz时，腔场的幅度(a)、相位(b)和控制器的输出(c、d)Fig.13 Amplitude(a)and phase(b)of the cavity field,and the output(c,d)of the LLRF controller in locked SEL mode under the detuning frequency of 5 Hz

图14 仿真腔体有不同恒定失谐时，locked SEL系统的入射电压幅度(a)、反射电压幅度(b)、腔场梯度(c)、腔场相位(d)v的响应曲线Fig.14 Response curves of the forward voltage(a),reflect voltage(b),cavity gradient(c)and the phase(d)of cavity simulator under the locked SEL system when the cavity is constantly detuned the different frequencies

4 结语

本文设计并开发了用于1.3 GHz连续波超导RF腔的数字低电平控制系统。低电平控制系统包含三种工作模式。GDR模式适合在腔体谐振时工作。Free SEL模式可以跟踪谐振腔频率，适合在腔体有较大失谐时工作。locked SEL模式适合腔体少量失谐时工作，可用于补偿腔体失谐的影响。在这项研究中，system generator的使用，可以快速实现和验证新的LLRF控制系统或算法。本文还开发了数字模拟腔，以降低测试过程中腔体损坏的风险，轻松测试先进的低电平算法。未来将设计和开发更高效，更准确的CORDIC模块。数字模拟腔还将会把洛伦兹力失谐，束流负载和麦克风噪声［3‒4，6］考虑在内，以实现对RF腔体的更真实的仿真。