倾斜摄影技术的单体塔式建筑物三维重建方法

王晓东，岳军红，陈兴芳

(1.西宁市测绘院，西宁 810001；2.陕西铁路工程职业技术学院，陕西 渭南 714000)

0 引言

为满足再现地理场景的需求，需利用现有数据构建实景三维模型用于地籍测量、智慧城市建设、灾害评估等领域[1].地理场景中存在一类形状不规则、高大、纹理单一的塔式建筑物，增加了实景三维模型构建的难度，制约着三维地理场景构建的发展[2].常用的建筑物三维建模可以通过手动、半自动人机交互以及全自动方法实现[3].虽然利用3DMAX、Auto-CAD 软件手动构建建筑物三维模型精度高，但是耗时长、成本高、覆盖区域小，适合城市重点区域精细化三维模型构建应用场景.Heo Joon 等[4]利用激光扫描仪获取点云数据构建建筑物三维模型，该方法采集成本高且获取三维模型缺少纹理信息，需要后期补拍影像以获取三维模型的纹理信息；张文春等[5]利用无人机拍摄影像数据与激光雷达(LiPAR)获取点云数据融合构建三维模型，能进一步提高复杂建筑物三维模型精度，但该类方法增加了三维建模的难度与成本；基于倾斜无人机摄影测量的三维模型自动构建技术[6-8]，通过不同视角获取多视影像数据构建实景三维模型效果较好，其精度有待进一步提高.塔式建筑物相对常规建筑物具有单独特征：外形结构复杂、纹理丰富、影像数据变形较大，因此建模复杂难度增加.采用常规倾斜无人机采集数据，航高与摄影倾斜角固定容易出现拍摄盲区导致获取的影像信息不全[9]；塔式建筑物一般高度较高，需要多次采集，造成数据冗余、建模效率低等问题，同时也可能因影像重叠度不足导致三维模型构建失败[10].因此，目前依然缺少一种适合塔式建筑物的三维模型构建方法.

本文针对单体塔式建筑物建筑外形结构复杂、纹理丰富、影像数据变形较大的特点，提出一种倾斜摄影技术的单体塔式建筑物三维模型构建方法.该方法利用多旋翼无人机平台搭载单镜头相机作为数据采集设备，通过环线航拍规划模型生成环绕式的航路，实现高效率对塔式单体建筑物多视角、多高度、三维立体自动航拍，以获取高质量的影像数据，进而提高构建实景三维模型质量与建模效率；通过建模效率、建模质量两方面对实景三维模型构建方法进行评价.

1 倾斜无人机单镜头三维模型构建方法

1.1 倾斜无人机系统

经纬M600Pro 无人机是大疆创新科技有限公司自主研发的垂直起降多旋翼无人机，M600 Pro搭载专业级A3Pro 飞控系统，配备三套惯性测量单元(IMU)与全球卫星导航系统(GNSS)模块，配合软件解析余度实现6 路冗余导航系统；安装避震设计处理，数据更精确，能有效地保障飞行器稳定可靠与精准操控.在六轴或八轴飞行器出现动力故障时，容错控制系统可以确保飞行器稳定飞行，确保飞行安全；具有可悬停拍摄、对起飞和降落环境要求低以及获取高精度的航测数据等优势.多旋翼无人机如图1 所示(搭载禅思H20 变焦相机)，具体参数如表1 所示.

图1 经纬M600Pro 无人机

表1 经纬M600Pro 飞行平台参数

1.2 环线航线规划

首先计算建筑物最小外包矩形，以矩形的底面中心点为球心，构建包含最小外包矩形的半球面；然后在半球面外侧构建一个同心面作为无人机航线范围，通过设置无人机航摄平台的相对航高与半径，使其能够围绕单体塔式建筑物飞行；利用地面控制系统进行调整，使相机镜头始终朝向球心，实现对同一建筑物多角度拍摄以避免出现拍摄盲区.

环线航摄模型输入参数包含：塔式建筑物最小外界矩形参数、相对航高、航向重叠度、旁向重叠度、相机焦距、影像成像分辨率、相机垂直、水平视场角度.环线航摄模型的输出参数包含：每条环线航拍的绝对航高、环线航拍的视场角度、环线航拍的半径.采用单向螺旋上升线的形式，环绕航线上每点的航高实时变化对地面控制系统要求较高，同时可能会存在在下一条螺旋线点影像的航向重叠度不能满足规定要求.为了保证航线间影像重叠度，采用固定航高的拍摄方式获取影像数据.为了保证采集塔式建筑物信息完整性，在规划环线航摄路线时需要考虑同一环线航向影像重叠度和相邻环线航拍间影像重叠度.影像重叠度设置错误会导致三维模型构建失败或增加数据冗余度，降低数据处理质量.环线规划航拍的模型流程如图2 所示.

步骤1:首先依据塔式建筑物的长、宽、高，计算塔式建筑物最小外接矩形长、宽、高；然后构建最小外接矩形对应的最小外包半球面；根据影像空间分辨率、相机像素大小以及相机焦距参数，计算相机中心相对被拍摄建筑物的距离，结合半球面球心参数构建一个半球面作为航行线路，即两个半球面的半径差为相机中心到被拍摄建筑物的距离，从而确定规划航线的球面半径大小.

图2 环线规划摄影模型流程图

步骤2:初始航高的确定.图3(b)为塔式建筑物最小外接矩形、最小外包半球面以及航线规划半球面的垂直截面，以C3和C4表示倾斜无人机在规划航线半球面上不同航高的两条环线上的相机位置，O为塔式建筑物的最小外接矩形圆心，OC3、OC4为相机中心与球心的连线的中轴线，θv为相机垂直方向的视场角大小，P7、P8、P9、P10为垂直方向视场角与最小外包半球面的交点.假设相机中轴线与水平地面的夹角为相机倾角α，可以获得该点的航高.为保证塔式建筑物信息的完整性，初始航高一般取中轴线与建筑物底部的角点上，但考虑建筑物底部周围可能存在的遮挡物(限制航高)，故取初始航高与限制航高的最大值作为最终的初始航高.

图3 环线规划摄影方式

步骤3:根据航向重叠度计算航线内拍摄间隔角度.如图3(c)所示，C1、C2为同一航线上相邻相机拍摄位置，O′为环绕航线的圆心，β为相邻相机拍摄点在环线上的夹角，θh为相机在航线上的水平方向的视场角大小，P3和P4为相机中轴线与最小外包半球面的交点，过P3或P4点做平行环线的水平截面，P1、P2、P5、P6为C1、C2点相机水平视场角边点与该水平截面的角点.将计算相机C1、C2航向重叠度问题转换为计算两点在水平方向重叠区域弧长与水平弧长的比值，即计算弧长与弧长或弧长的比值.假设相机C1和C2位置航高为h，航向重叠度Oc，r1为最小外包球面的半径，r2为航线上半径大小，依据相机的水平视场角θh反算出β，如式(1)：

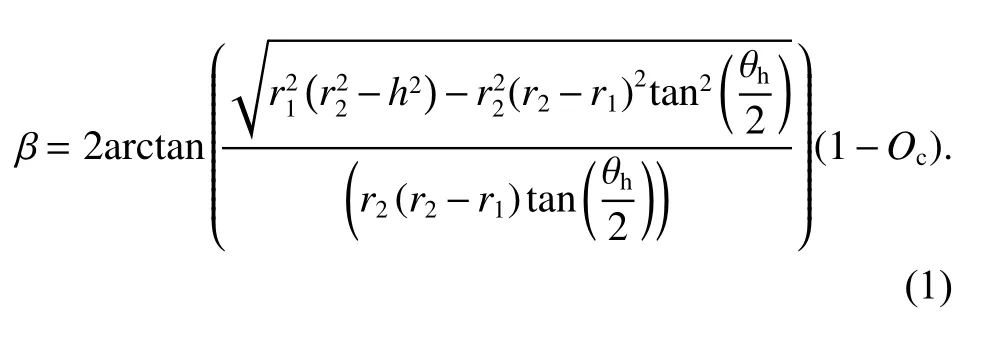
步骤4:判断当前航高相机垂直视场角的最低点是否覆盖塔式建筑物的顶部，若相机垂直方向最低视场角覆盖塔式建筑物的顶部，则终止计算并输出每条环绕航路的航高、每条环绕航线的半径和每条环绕航路的摄影间隔角，否则执行步骤5.如图3(b)所示，假设C4为当前环线航拍线路的下一个环线航拍的相机位置，则相机垂直视场角最低点覆盖建筑的判断条件为：∠P7C4O>∠P7C4P9.

步骤5:根据航向旁向重叠度计算下一条环线航高.如图3(c)所示，航线旁向重叠度计算与航向重叠度的计算原理相同，将旁向重叠度计算问题转为垂直方向弧线比值的计算问题.假设输入旁向重叠度为Os，相机垂直方向的视场角θv，C3航线的航高h1，依据式(2)与C3相邻的航线C4航线航高，即为下一条航线的航高.计算公式如式(2)：

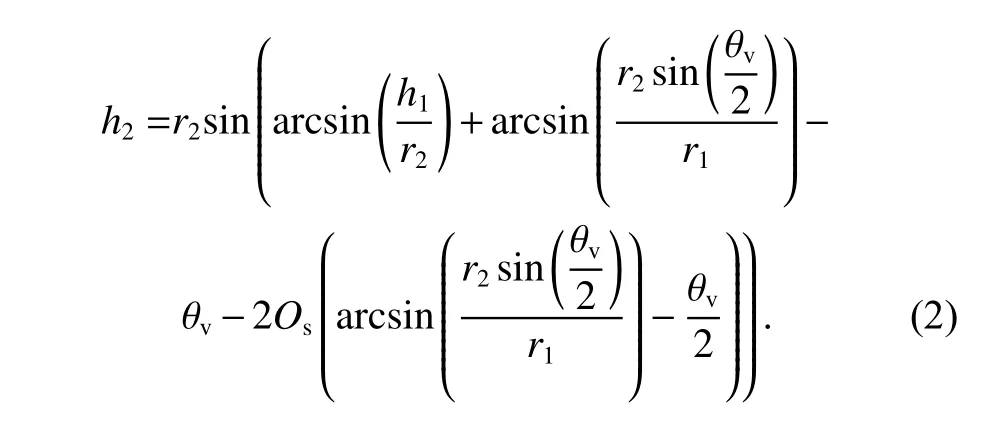
步骤6：参考步骤3 的计算方法计算该航高下环线拍摄的间隔角度，并跳转至步骤4.

1.3 多视影像数据处理

利用地面控制系统规划单镜头倾斜无人机采集塔式建筑物的环线飞行航线，通过单镜头无人机倾斜系统采集建筑物多视影像数据，结合成熟的多视影像处理系统构建塔式建筑物实景三维模型.具体多视影像实景三维重建流程如下：首先，利用多视影像数据、影像对应的姿态数据进行多视影像匹配处理生成影像间稀疏同名点坐标，通过对极几何约束、比例尺约束以及视差约束等多种约束策略剔除初始同名点存在明显错误的点对[11]；其次，进行光束法区域网平差算法计算连接点的物方空间坐标以及每张影像精确的外方位元素信息；再次，通过多视影像密集匹配算法获得多视影像的同名点坐标，依据多片前方交会算法计算多视同名点的物方空间坐标生成物方密集点云数据，并计算每个点云的法向量、构建不规则三角网(TIN)[12]；最后，利用纹理自动映射技术，对每个TIN 选择最优的影像面片，生成最终的塔式建筑物实景三维模型[13-14].具体多视影像数据处理流程如图4 所示.

图4 多视影像数据处理流程

1.4 精度验证

为了验证采用环线航拍获取多视影像数据构建实景三维模型的精度，文中从纹理细节信息、控制点误差以及整体模型复杂程度等方面进行验证.其中，纹理细节信息能较好地表现模型完整性，从而验证纹理相对几何关系和纹理缺失情况；控制点误差能较好地反映构建三维模型的绝对精度，采用式(3)计算控制点的点位误差；依据三维模型复杂规范《三维地理信息模型数据产品规范》[15]，通过三维模型的旋转和缩放对实景三维模型纹理、颜色、完整度进行定性评价的方法评估三维模型复杂程度.

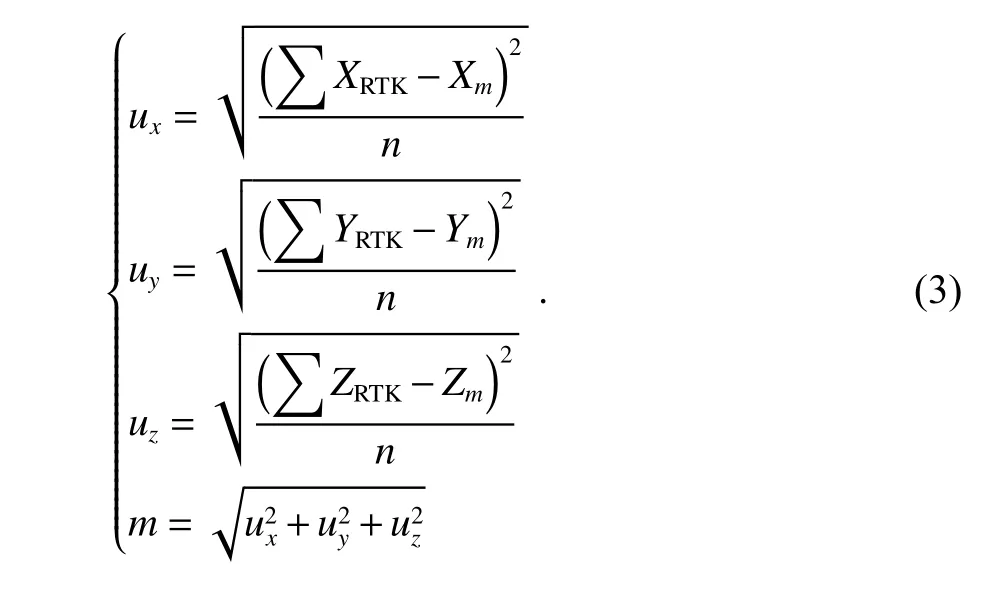
式中：ux、uy与uz为模型上量测坐标与外业采集控制点坐标在X、Y、Z方向的误差；n为控制点点数；(xRTK,yRTK,zRTK) 与(xm,ym,zm)分别为外业控制点坐标与三维模型量测坐标；m为控制点的中误差.

2 环拍实验

为了验证本文论述方法的可行性，选择韶关市的某塔作为试验对象，该塔曾为岭南名胜“曲江二十四景”之一，在塔西南方向曾出土过大量的青砖、瓦片和砖制构件，该文物具有建筑考古价值.此塔位于呈椭圆的小岛上，东西最宽处约36m，南北最长处约68m，面积约1680m2.

2.1 数据采集

针对塔式建筑物高、纹理丰富、拍摄影像局部变形较大的特征，采用大疆公司开发的飞控软件DJIGS Pro 设计环线，输入环线参数为：设置最低航高为15m、最高航高为70m、相机水平视角45°、垂直视角25°、旁向重叠度85%、航向重叠度60%，规划生成23 条航线、最小外接球半径70m、影像拍摄分辨率2dpi，共采集1027 张影像数据，环线规划图如图5 所示.

图5 环线规划示意图

2.2 三维建模

由于拍摄影像数据存在几何变形，依据拍摄时相机与塔式建筑物的距离关系.首先，将影像投影到固定距离面上，以减少影像几何变形的影响；其次，对多视影像数据利用尺度不变特征变换(SIFT)算法计算影像初始匹配同名点，通过对极几何约束、比例尺约束以及视差约束等多种约束策略剔除初始匹配同名点的误匹配点对获取定位精度较高的同名点对；再次利用ContextCapture Center Master 三维建模软件进行空三处理获取同名点的物方空间坐标以及精化后的影像姿态数据.影像空三处理后，塔式建筑物周围存在噪声与冗余的点云数据，由于采用环绕航拍塔式建筑使得中心区域点云密集生成三维模型效果较好，通过手动剔除周围噪声点云，确定空三后的稀疏点云数据；然后，采用三维多视角立体视觉算法(PMVS)生成高密度的密集点云，通过直线段检测算法(LSD)检测点云上的线特征并以特征边为约束构建TIN，确保塔式建筑物的边缘信息完整；最后，对生成的不规则三角网进行纹理自动映射生成最终塔式建筑物的实景三维模型，整体三维模型如图6(a)所示.

图6 实景三维模型

2.3 三维模型精度验证

1)模型精度分析

为了验证生成三维模型的精度，利用实时动态(RTK)与全站仪采集外业控制点坐标，并在生成的三维模型上量测对应点的空间坐标，通过对比两套坐标的差异统计控制点的点位误差.将外业采集的控制点左边以及量测的三维空间坐标统一转换到WGS84_UTM_49N 带高斯投影面上，控制点外业测量结果与三维模型量测结果如表2 所示(为了保密需要采用**表示前几位坐标)，其中，DX、DY、DZ为两个坐标的差值.利用式(3)计算控制点的误差并统计X、Y、Z方向的中误差，由表2 可知每个控制点的均方根误差(RMSE)都在厘米级别，其中，X、Y、Z方向的最大误差分别为0.037m、0.043m、−0.045m；最小误差分别为0.011m、−0.014m、0.029m；X、Y、Z三个方向的中误差分别为0.023m、0.029m、0.037m，没有出现明显的过大或过小误差整体满足1:500 比例尺三维模型精度需要，检查点具体误差分布如图7 所示；实验表明采用环线航拍模式获取多视影像数据，通过影像匹配、空三处理、密集匹配、不规则三角网生成、纹理自动映射等步骤数据处理，构建单体塔式建筑物三维模型精度较好.

表2 控制点坐标误差统计m

2)模型细节

文中选取3 个代表性的局部细节信息，以评价生成模型的细节质量，由图6(b)～(d)3 组细节模型可知：塔式建筑物的局部人物构建细节清晰，能清楚地表达人物的微妙形象；在塔式建筑物的塔尖、围栏区域没有存在变形，线特征明显、细节信息完整；整体模型完整性较好、各模型细节表达清晰没有出现明显的纹理信息缺失区域；整体贴图色调均匀，没有出现明显的拉花或变形现象，能够较好的反应古塔的表面真实信息、空间位置信息以及属性信息.总体来说，整个实景三维模型能够完整准确真实地对古塔进行三维重建，模型细节表达完整.

图7 检查点误差分布图

3 结束语

针对塔式建筑物构建三维模型容易失败问题，采用环线航拍的方式获取塔式建筑物的多视影像数据，弥补由于建筑物周围地物遮挡以及自身结构特点导致的拍摄盲区，增加采集数据的有效性；通过利用成熟的三维建模软件能够构建定位精度较高、纹理清晰、细节完整的实景三维模型，有效地提升塔式古建筑物的保护工作.但文中缺少规划不同半圆球半径采集多视数据构建三维模型实验，将是下一步工作研究的重点.