考虑电动汽车虚拟储能的高渗透配电网鲁棒优化调度

田壁源，常喜强，徐海奇，刘琪，，张新燕

（1.国网新疆电力有限公司 乌鲁木齐供电公司，乌鲁木齐830011；2.国网新疆电力有限公司，乌鲁木齐830018；3.新疆大学 电气工程学院，乌鲁木齐830047）

0 引言

近年来，为应对气候变化、推动绿色发展，电动汽车（electric vehicle，EV）和可再生分布式电源（renewable distributed generation，RDG）得到了广泛发展与应用。电动汽车的日益普及在减少二氧化碳排放、缓解能源危机等方面发挥着巨大的优势和潜能。与此同时，各类RDG包括风力机（wind turbine，WT）、光伏（photovoltaic，PV）等，由于具有清洁特性，未来将和EV一起大规模接入配电网［1］。然而，大量高渗透率、强波动性RDG以及大规模EV无序充电负荷的接入，必将进一步加大负荷峰谷差，为配电网的安全稳定经济运行带来巨大挑战。

EV车载动力电池具有典型的负荷和电源双重属性，其额定容量远远超过车主日行驶里程的需求，通过构建电动汽车虚拟储能（EV virtual energy storage，EV-VES）系统［2］，并制定合理的EV-VES充放电时序及功率计划，不仅可以逆转因大量EV负荷的存在而给电网稳定运行带来的负面影响，还能显著改善电网的经济效益和运行状况。

目前，针对EV-VES参与电网削峰填谷、提供辅助服务和促进新能源消纳方面研究较多。而对EV充电负荷的时空特性及随机性研究较少，对EV充电负荷分类研究也不够全面。另一方面，大量具有不确定性特征且不可控的RDG接入，给配电网优化运行带来了巨大风险。因此，在考虑不确定性的可再生能源优化调度问题中应用鲁棒随机优化理论，对提升系统运行的鲁棒性具有重要作用。

在此背景下，以EV与RDG协同优化、负荷削峰填谷和平滑可再生能源输出为出发点，开展了大规模EV和高比例RDG接入场景下的配电网优化调度问题研究。首先，量化分析了EV-VES与RDG的协同优化效果，基于各类EV全天的停驶特点，建立了可供调度的EV-VES容量估算模型；然后，通过引入鲁棒系数和预测误差参数处理风电、光伏出力的不确定性，综合考虑EV用户充电满意度与及电池性能等约束，建立了以调度周期内负荷波动最小和EV用能成本最低为目标的EV有序充放电调度模型；最后，以某地区配电网实际运行数据进行仿真，验证了所提模型与求解方法的可行性与有效性。

1 电动汽车虚拟储能模型

1.1 电动汽车与可再生能源出力关系

EV作为一种入网的可控负荷，在受控状态下可作为储能单元向电网进行充放电，规模化场景下可提供规模可观的灵活性资源，具有巨大的负荷调控潜力，能够有效提升电力系统对可再生能源的消纳能力［3］。为评估电动汽车虚拟储能的调节效果，仅考虑电动汽车灵活性资源对风电、光伏发电波动性的调平效果。

图1为某城市电网典型工作日的负荷、分布式风电、光伏出力与EV充电桩使用率曲线。

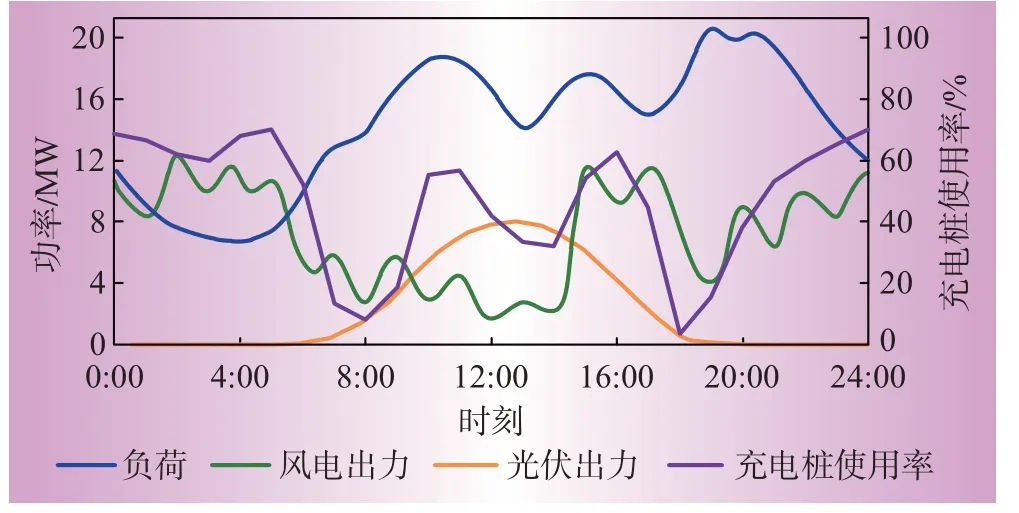
图1 电网负荷、分布式风/光出力与充电桩使用率曲线Fig.1 Load,distributed wind/PV power output and charging pile utilization rate curves

由图1可知，EV用户选择充电的时段大多在日间的工作时段和夜间，这与风电和光伏的最大出力时段重合，有助于消纳可再生能源。但电动汽车出行高峰时段之后，充电桩的使用率与系统负荷同时增长，此时EV无序充电会加大电网负荷的峰谷差，导致系统运行成本增加。

1.2 可再生能源消纳量

由于风能和太阳能供电能力的随机性，所以认为它们是不可调度的，输出的电能能够实现就地消纳。因此，PRDG,t为t时刻RDG总的输出功率，待消纳量SRDG即为分布式风电、光伏发电总量，则

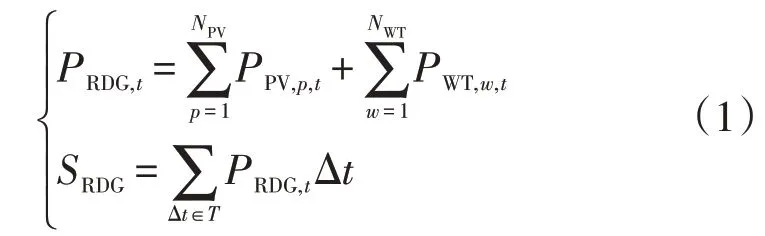
式中：NPV、NWT分别为分布式光伏与风电的数量；PPV,p,t为t时刻分布式光伏p的输出功率；PWT,w,t为t时刻分布式风电w的输出功率。

1.3 电动汽车能源供给模式

目前，EV充电主要通过充电桩进行，在城市中电动汽车的充电方式主要有2种：交流慢充（目的地充电）和直流快充（快速充电站）。EV慢充需求通常包含2种情况：①白天主要分布在工作场所周围，该EV充电需求可以消纳分布式光伏发电；②夜间主要分布在家庭小区周围，该EV充电需求可以消纳具有反调峰特性的风力发电，是实现EV与可再生能源发电协同的最直接方式。但慢充难以及时满足EV用户迫切的能源需求，对行驶时间大于停驶时间的车辆而言，快充是其重要的电能补充方式，EV的快充需求一般集中在白天及夜间凌晨时段，与光伏的出力时段和夜间风电高发时段相互吻合，是消纳可再生能源的重要方式；然而无序的EV快充也将带来尖峰负荷、电压降落和网络损耗等问题。因此，可将EV慢充与快充相互协调，共同实现与可再生能源的协同。

1.4 电动汽车充放电时序分类

电动汽车的出行用途与车辆类型对其充电模式具有重要影响［4］。结合我国电动汽车使用及发展现状，将电动汽车按出行特点分为4类。

A类：电动计程车，计程车通常由2名以上司机倒班驾驶运营，由于充电时间紧迫，仅在交班前或剩余电量降至阀值时采取快充方式进行充电。

B类：电动私家车，一天中在居住地和工作地往返一次，停车时间长且充电时间充裕，多在居住地或工作地进行充电，通常选择慢充方式。

C类：电动功能车；包括商务车和小型货物用车等，其出行在时间上呈间断分布，出行时间相对稳定，视出行时间情况选择快充或慢充。

D类：电动公交车；公交车出行时间及里程相对固定，多采用换电或慢充方式，充电负荷稳定。

1.5 电动汽车储能数学模型

VES车辆能够提供的可用储能容量与EV数量、EV实体状况（起始荷电状态（state of charge，SOC）、电池容量、电动汽车工作功率、效率、百公里耗电量等）、车辆全天时段的停驶状态、EV车主诉求预留行驶需求等有关。假设在EV-VES服务中的EV电池系统均采用衡功率工作模式，单辆EV可持续服务时间为

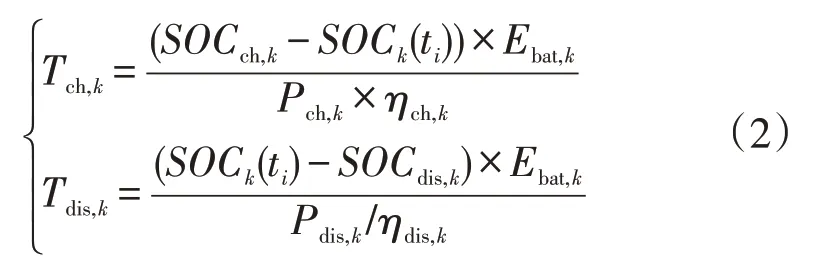
式中：Tch、Tdis分别为单辆EV参与VES服务的充电时间及放电时间；SOCk(ti)为ti时刻EV各自电池的荷电状态；SOCch为EV参与VES充电服务预计达到的能量状态；SOCdis为预留备用出行的能量比；Ebat为EV各自的电池可用容量；Pch,k、Pdis,k与ηch,k、ηdis,k分别为第k辆EV的充、放电功率及效率。

1.6 电动汽车聚合充放容量建模

本文将多个EV储能聚合成一个等效的虚拟储能单元供调度中心进行调度，在调度优化计算时只需一个集中EV-VES的充、放电变量，包括EV-VES系统的充放、电功率及可用储能容量，具体如下

（1）EV-VES系统总功率

式中：Pch,total,t、Pdis,total,t分别为t时刻EV总的充电、放电功率；λk,t为t时刻第k辆EV的充、放电状态；

（2）EV-VES系统总可用储能容量

基于单辆EV实体的可用容量求解模型，通过实时累积得ti时刻可供调用的EV群体储能容量为

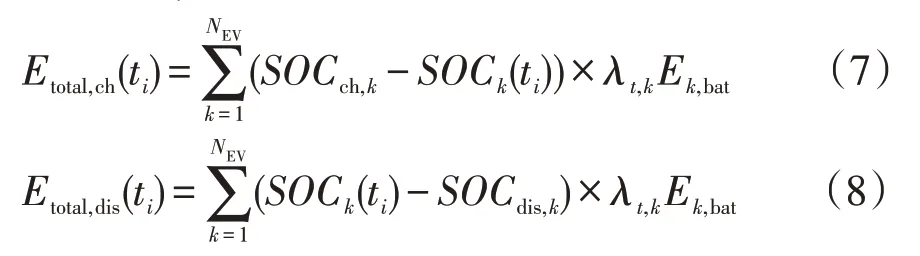
式中：Etotal,ch(ti)、Etotal,dis(ti)分别为ti时刻可用储能充电容量总和；NEV为参与调度的EV数量。

1.7 EV-VES系统稳态建模

EV-VES系统充放电功率为：

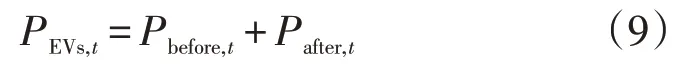
式中：PEVs,t为EV-VES系统的充放能功率值（充电为正，放电为负）；Pbefore,t、Pafter,t分别为应用EV-VES系统前后的配电网负荷值。

2 鲁棒优化调度模型

2.1 风光出力不确定性描述

鲁棒随机优化理论将各种可能的场景设定为一个不确定集合，使得寻找出的最优解对集合内每一元素可能造成的不良影响具有一定的抑制性，通过调节鲁棒系数即可决策出不同程度上抑制不确定性影响的优化调度方案。在高比例可再生能源配电网中，风电、光伏出力具有明显的不确定性，其输出功率并不能被准确的模拟和预测，但可基于预测结果的形式进行克服，不确定范围计算如下

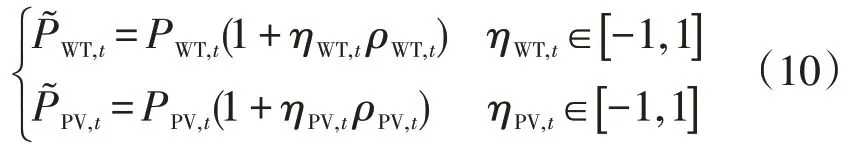
考虑在实际运行过程中，风光发电往往难以达到最极端条件，分别引入风电、光伏发电鲁棒系数ΓWT、ΓPV，Γ∈[]0,1，建立具有自由调节鲁棒系数的随机优化模型如下

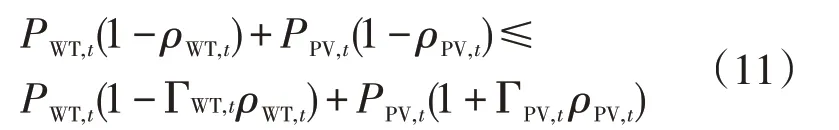
2.2 目标函数

（1）电网净负荷方差最小

大规模分布式风电、光伏以及EV无序充电负荷的接入将会影响配电网的正常运行。因此，以系统净负荷曲线的标准差最小为优化目标，具体目标函数如下

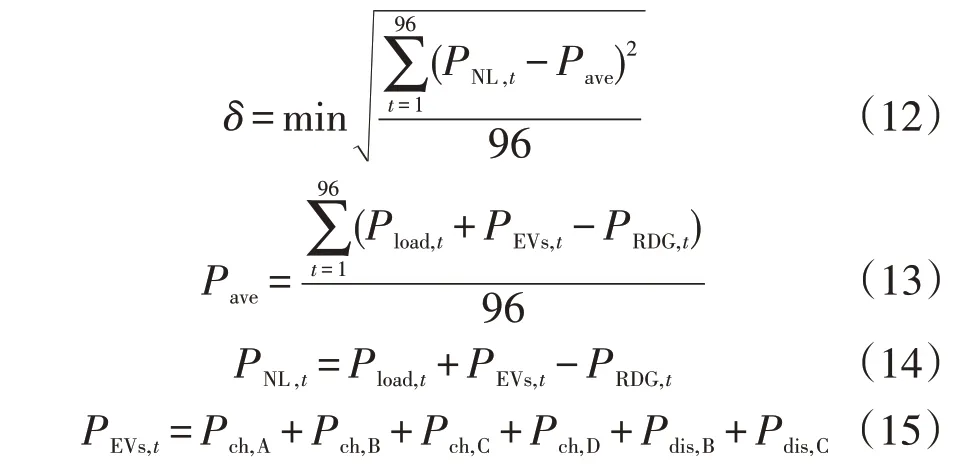
式中：Pload,t、PNL,t、PRDG,t、PEVs,t分别为t时刻的配电网常规负荷、净负荷、可再生能源出力及电动汽车充放电负荷，由A、B、C、D 4类电动汽车负荷数据构成；Pch,t、Pdis,t分别为t时段电动汽车充、放电功率；设定日负荷采集时间间隔为15 min，每15 min下发1次调度指令，Pave为每天96个时段的等效负荷平均值。

（2）EV用户成本最小

以辅助调峰价格为引导，将EV用户成本最低作为优化目标，包括EV充电费用及EV参与电网调峰收益，具体目标函数如下

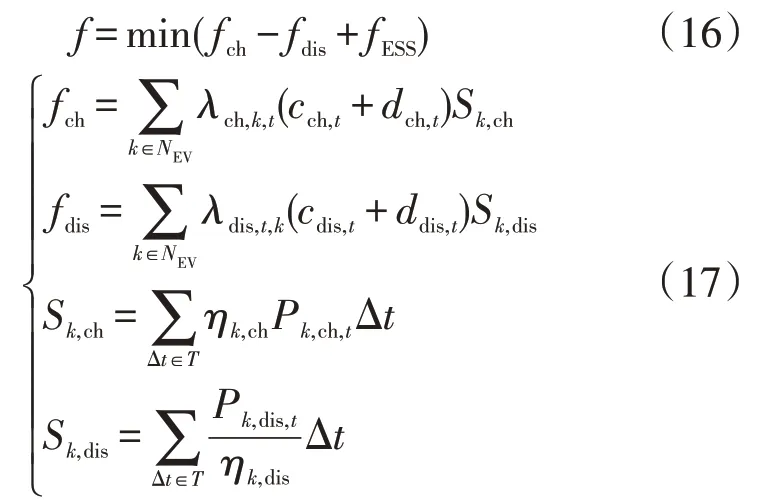
式中：f为EV用户用电成本；fESS为EV电池的充放电损耗成本；fch、fdis分别为EV充电支出与放电收益；NEV为EV数量；Δt为单位时段；Sk,ch、Sk,dis分别为周期T内k辆EV的充电电量与放电电量；cch,t、cdis,t与dch,t、ddis,t分别为t时刻EV的充电、放电价格和参与调峰的补偿/惩罚价格。

2.3 约束条件

（1）功率平衡约束

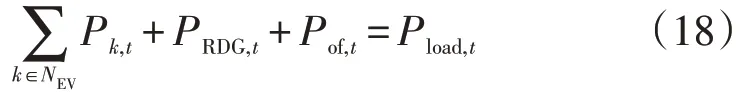
式中：Pof,t为t时刻配电网的下网负荷。

（2）EV充放电约束

EV电池的荷电状态受充放电效率及上一时刻电池状态影响，其当前时刻的荷电状态为

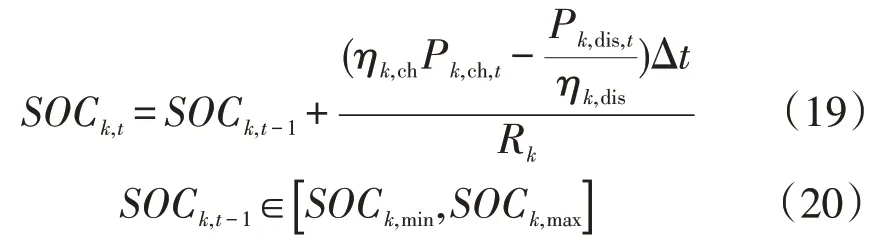
式中：SOCk,t为第k辆EV的荷电状态；SOCk,max、SOCk,min分别为第k辆EV电池的最大、最小允许荷电状态；Rk第k辆EV电池的额定容量。

（3）EV电池约束

电池约束主要有电流约束和容量约束。考虑车主自身出行需求及电池损耗，需限制深放深充行为，同时EV充放电功率不能高于额定充放电功率

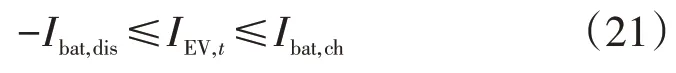
式中：Ibat,ch、Ibat,dis分别为EV的最大充、放电电流。

（4）EV用户充电满意度

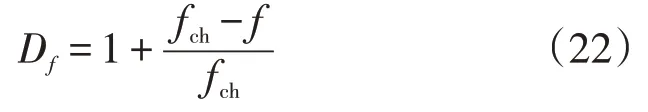
式中：Df为EV用户充电满意度。

2.4 模型求解

结合上述约束条件和目标函数，建立了多目标优化模型，即在调度周期内使得负荷波动最小和电动汽车用能成本最低。为了尽可能消纳分布式风电、光伏发电，本文假设调度周期内分布式风电、光伏预测出力全额并网，作为负的负荷并入到配电网总负荷当中。通常情况下，若整个系统总负荷波动达到最小时，将导致电动汽车用能成本相对较大，反之，用能成本最小时，负荷波动幅度难以达到要求。因此，为了获得最优解，对上述建立的模型设置权重系数，将所建立的多目标优化模型转化为单目标优化模型，具体做法如下：

（1）以调度周期内系统总负荷波动最小作为目标函数求解所提模型，得到总负荷波动最小值δmin和此时电动汽车用能成本；

（2）以电动汽车用能成本最低作为优化目标，求解所提模型，得到用能成本最小值fmin和此时的总负荷波动值；

（3）由于目标函数的优化方向不同，故在进行多目标加权为单目标时，需要进行相应的处理，设定ωδ和ωf分别为配电网总负荷波动最小和电动汽车用能成本最低的权重系数，则可对目标函数进行加权处理，具体如下

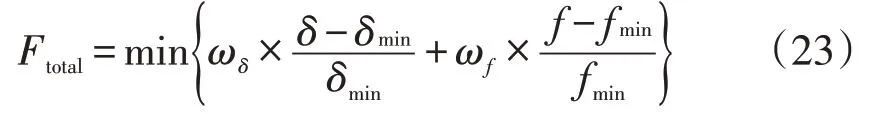
ωδ和ωf给定后，可以计算得出最小配电网负荷波动和最低的电动汽车用能成本。

多目标粒子群优化（multi-objective particle swarm optimization，MO-PSO）算法寻优是一个逐步迭代逼近真实Pareto前沿的过程，可在计算过程中持续改变目标函数的权重，使得粒子群在Pareto最优前沿上移动，获得最优Pareto前沿。本文采用动态加权MO-PSO对子目标函数赋权的过程进行动态化处理，在N次迭代过程中，权重系数的计算公式为

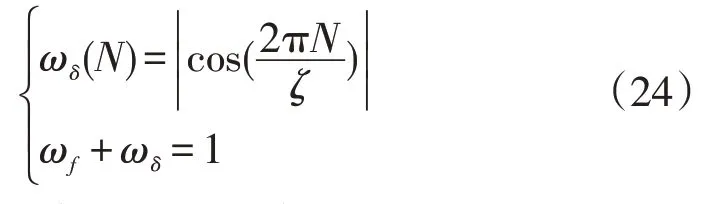
粒子运动速度的更新公式为

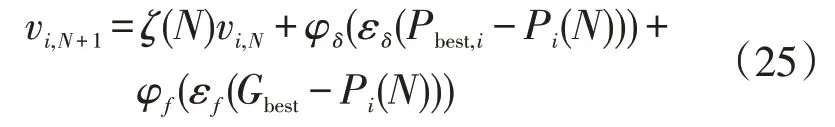
式中：vi,N为粒子xi在本次迭代计算中的速度；εδ与εf分别为［0，1］区间内相互独立的随机数；Pbest,i为该粒子目前最优位置；Gbest为全局最优位置；惯性常数ζ(N)取值在［0，1］线性递减，从而使得搜索空间不断缩小。

粒子位置的更新公式为

通过上述方法，可在计算过程中持续改变目标函数的权重，使得粒子群在Pareto最优前沿上移动，获得Pareto最优解集，并从所有选择中选出一个作为最佳折中解，求解步骤见文献［5］。

3 算例分析

3.1 算例数据

文中策略以电动汽车大规模应用、充电设施建设普及为背景，应用场景为停车场模式，每个车位配备1个充电桩。假定该区域内共有200辆A类车、600辆B类车、200辆C类车、200辆D类车，各类车型的起始和返程出行概率分布见文献［6］。假设电动汽车电池容量为60 kWh，充电桩的快充功率为60 kW，慢充/放功率均为20 kW，充放电效率均为0.95；车辆起始出行的SOC范围为0.8~0.9，SOC上限为0.9，下限为0.2，fESS为0.2元/kWh。粒子群算法中取粒子数为20，最大迭代次数为300，最大速度为0.4，惯性权重在［0.2，0.95］内线性递增。

典型日某地区配电网常规负荷、EV充电负荷及分布式风光出力预测标幺值曲线如图2所示，其中配网常规负荷基准值为40 MW，EV充电负荷准值为15 MW，分布式风电和光伏出力基准值为50 MW。将时长24 h作为一个调度周期，参考电力系统调度的控制周期T=15 min，对96个时段内电动汽车作为移动储能参与虚拟储能的情况进行分析。

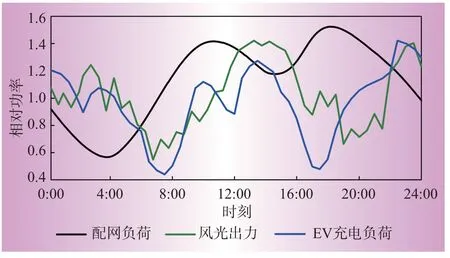
图2 典型日配网负荷、EV充电负荷及风光出力预测值Fig.2 Typical daily distribution network load，EV charging load and forecast value of wind and solar output

3.2 EV-VES系统调度计划

以系统经济最优、供电可靠性最高为目标获得典型日内该配电网削峰填谷需求如图3所示。

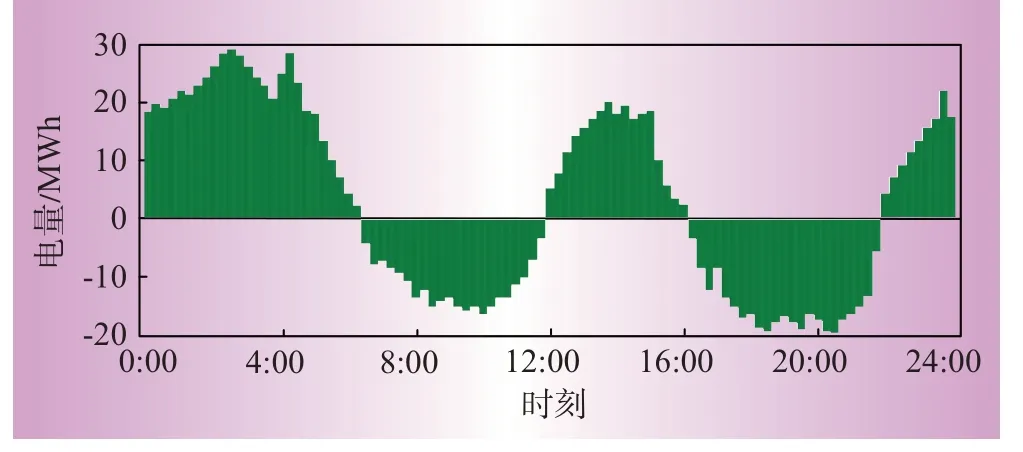
图3 削峰填谷需求Fig.3 Peak load cutting and valley filling demand

根据各类型电动汽车日停驶状态、电网负荷削峰填谷需求和风光出力预测情况，设计了各类EV在一个调度周期内的充放电时序，如图4所示。考虑到A、D 2类车长期处于行驶状态，运营时间规律，车辆充电量较大且易于集中管控，易于参与有序充电，因此将A类车参与EV-VES快充服务时间设置为2:00—6:00、12:00—15:00；D类车慢充服务时间设置为21:00—次日6:00。而B、C 2类车出行强度较小，停驶的时间较长，在参与有序充放电方面具有较好的灵活性及可调节性，同时B、C 2类车具有一定的时段互补性，因此将B类车参与慢充服务时间设为21:00—次日6:00，快充电服务时间设为12:00—15:00，放电时间设为9:00—12:00、15:00—21:00；C类车参与慢充服务时间设为21:00—次日8:00，快充电服务时间设为12:00—14:00，放电时间设为17:00—21:00。

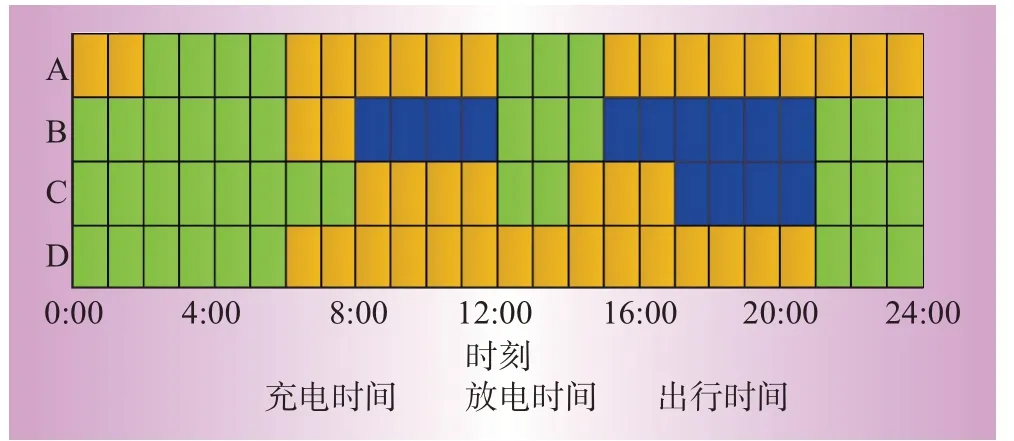
图4 不同类型电动汽车充放电时序Fig.4 Charging and discharging sequence of different types of EV

为降低EV无序充放电对削峰填谷效果的影响，在基础负荷低谷期及可再生能源发电富余时段（23:00—次日6:00、12:00—15:00），实行较低的EV充电电价，并根据RDG出力情况制定灵活的调峰补偿价格，促进EV负荷与RDG出力的协同。同时，为引导EV进行集中放电，在负荷高峰且可再生能源出力较低时段（8:00—12:00、15:00—21:00），允许EV进行并网放电，并获得相应时段的调峰补偿，达到削峰效果。分时电价、EV动态充放电电价及辅助调峰补偿价格如图5所示。

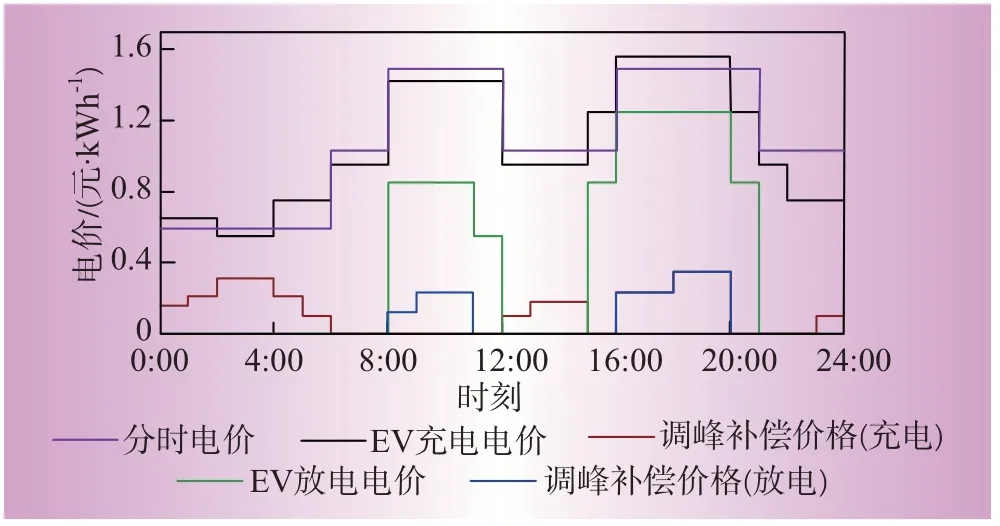
图5 分时电价、EV充/放电价及辅助调峰补偿价格曲线Fig.5 Time-of-use price，EV charging/discharging price and auxiliary peak shaving compensation price curves

假设EV-VES服务中电动汽车以额定功率放电，根据式（4）—式（10）计算调度周期内各时段可供调用的最大EV-VES充放电容量如图6所示。

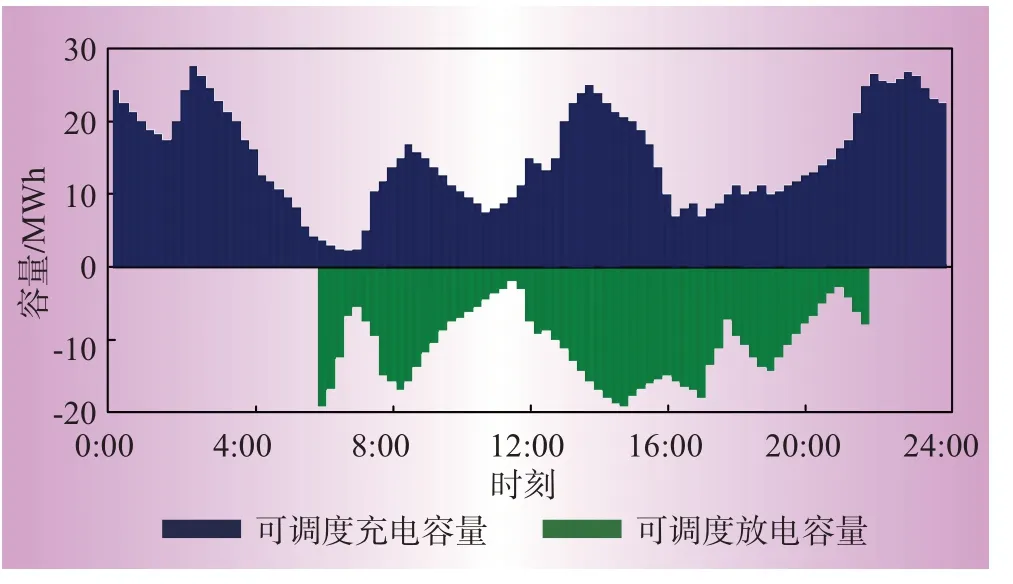
图6 各时段可调度EV-VES容量Fig.6 Schedulable EV-VES capacity in each period

3.3 调度结果分析

各时段由EV-VES所提供的充放电量如图7所示，可以看出，调度周期内96个时段的充放电量均能够满足电网削峰填谷调节需求，且能够提供缓解可再生分布式电源出力波动的平滑服务。

优化调度前后的EV用能成本、充电满意度及净负荷均方差如表1所示。其中，EV的无序充放电采用分时电价，有序充放电则采用动态充放电价和调峰补偿价格。由表1可见，EV有序充放电调度使EV用户用能成本降低了9.05%，EV用户充电满意度提高了8.52%，净负荷均方差下降了18.43%，可见EV-VES的参与可显著降低负荷峰谷差、平抑负荷波动，提高EV用户参与VES服务的积极性，验证了所提模型与求解方法的可行性与有效性。

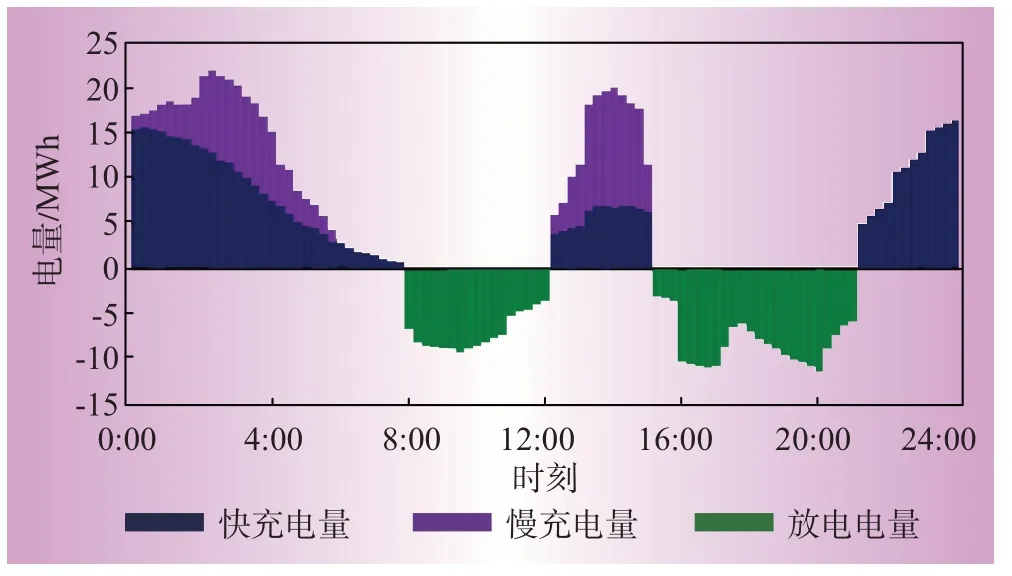
图7 电动汽车充放电调度结果Fig.7 EV charging and discharging scheduling results

表1 优化结果Table 1 Optimization results

为体现本文所提出的EV有序充放电调度模型和策略的效果，引入波动率y来评价配电网净负荷的波动水平，波动率采用式（27）计算，计算得到调控前后的净负荷波动率曲线如图8所示。

图8 净负荷波动率曲线Fig.8 Net load volatility curves

由图8可见，调控后的平均净负荷波动率为1.82%，低于调控前的3.76%，有效缓解因风电、光伏出力波动对电网造成的冲击，进一步验证了EV-VES系统在源侧协同可再生能源出力、在网侧参与削峰填谷的可行性。

4 结束语

本文针对RDG和EV大量接入后给配电网带来的挑战，研究了基于电网调峰及可再生能源消纳的EV有序充放电优化调度方法，提出了一种综合考虑EV接入随机性和RDG出力不确定性的鲁棒优化调度模型，建立了可供调度的EV-VES容量估算模型，并以调度周期内负荷波动最小和EV用能成本最低为目标构建了优化调度模型及求解算法。算例仿真结果表明：对EV的充放电价格、功率和时间进行集中优化控制，既能取得明显的削峰填谷效果，缓解风电、光伏出力波动对电网造成的冲击，同时又可以为EV用户获取更多的调峰补偿收益，缓解充电成本及车辆自身损耗成本，在总体上提高了配电网运行的经济性和鲁棒性，为电动汽车参与电网侧储能提供了理论依据。