基于电动汽车行驶数据快速聚类的充电站选址优化

2021-05-23王妍吴传申高山

电力需求侧管理 2021年3期

王妍，吴传申，高山

（1.东南大学电气工程学院，南京210096；2.江苏省智能电网技术与装备重点实验室，南京210096）

0 引言

近年来，电动汽车充电桩的建设发展飞速，需求量不断扩增，是国家“新型基础设施建设”工作领域的核心之一［1］。随着“新基建”政策的不断落实，公共充电站的数量有可能大量扩充，虽然给使用者带来了一定程度的便利，但同时也对电网的稳定性和可靠性提出了更高要求，带来了更多挑战。电动汽车虽然有很大的灵活性，但也可能造成电力系统的稳定性下降，带来电能质量问题。因此在大力发展电动汽车充电站的基础上，如何最大程度保证电网稳定性、优化年建设运维成本以及合理规划建设，是现在急需解决的问题［2］。

一些研究人员利用优化理论，从充电站最优经济收益的角度出发，仅考虑电动汽车充电站的经济效益而忽略了电动汽车使用者的使用便捷性和经济性。目前对于电动汽车充电站的优化管理主要采用随机优化［3］和多场景仿真［4］算法，较好地考虑了充电站的经济性，但缺乏对电动汽车使用者使用快捷性的考虑。文献［5］将网络交通车流信息转换成电动汽车的电量变化，继而根据电动汽车的电量需求变化对充电站进行优化管理，这一方法相对简单，但分析的准确性还有待提高。文献［6］将多周期最优潮流应用于电力系统的管理，保证了发电变化量和电动汽车集群的相互统一控制；文献［7］建立了基于马尔科夫链的交通仿真模型，在考虑交通流量的基础上，对城市路网系统中充电站的充电负荷进行预测，但此研究利用的是静态交通流量，与实际生产工程有明显差别。

以上文献对充电站的规划产生了不同的思考，但很少从电动汽车用户需求的角度去研究问题。电动汽车充电的有效时间通常不低于0.5 h。如果一辆电动汽车在一个地方停留超过0.5 h，而此时电动汽车与充电站距离较近，那么利用车主停留的这段有效时间对电动汽车进行充电，有利于减少车主的的成本花费。

北斗导航和GPS导航可以确定电动汽车的行驶轨迹，包含汽车驾驶模式、驾驶习惯等潜在信息，通过挖掘这些潜在信息，可以为城市道路与电动汽车充电站的合理规划建设提供宝贵的信息支持。如何通过提取电动汽车轨迹大数据，研究驾驶行为与城市建设的相关性，从而优化城市建设，成为国内外关注的热点之一［8］。

本文从电动汽车使用者和电动汽车充电站的经济性角度出发，利用大数据分析，研究电动汽车的行驶轨迹，并通过空间建模，采用谱聚类方法，将相似语义特性的汽车轨迹进行谱聚类，将城市空间划分为不同的类别，然后根据所得聚类结果对电动汽车充电站进行合理规划。本文将在规划的区域内，依据聚类结果，考虑电动汽车充电效率以及充电站建设的经济性，对充电站规划建设地点进行优先级排序。

1 电动汽车行驶轨迹数据及空间建模

采用向量空间建模，将非结构化车辆数据转换为结构化数据矩阵，为利用谱聚类算法分析电动汽车交通轨迹数据的特性提供结构化数据支持。

1.1 规划区域

将整个待规划地域定义为充电站规划空间A。按经度划分区域为[Lo,min,Lo,max]和按纬度划分区域为[La,min,La,max]，则规划空间表示如下

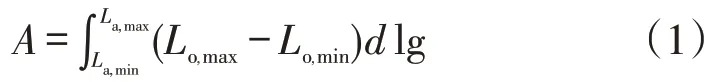
式中：La,max、La,min分别为充电站规划空间A纬度空间的上、下边界值；Lo,max、Lo,min分别为充电站规划空间A经度空间的左、右边界值。

1.2 网格空间

将规划区间A按纬度优先原则分划为M行和N列，形成的（M×N）个网格称为网格空间B，其中每个网格称为空间网格bi，（以下简称网格），即

式中：i为空间索引号；bi可用bm,n表示。

由1.1节和1.2节可知，规划区域A和网格空间B之间的关系为A≡B，且对于任意的i,j(i≠j)，满足bi⋂bj=Φ。在规划区域A中，任意给定一位置a(x,y)，都能在网格空间B中找到唯一的bi，使得a∈bi。

1.3 电动汽车行驶轨迹

把采集得到车辆i在行驶过程中的空间、时间及其它信息组成的时间序列称为行驶轨迹，即

式中：Ci=(oi,ai,ti)为包含经度、纬度和时间信息的时空数据；k=len(Ci)为行驶轨迹时间序列的长度。

假设接入轨迹数据平台的车辆有p辆，每辆车为矩阵的一列，路网空间的网格数为q个，每个网格为矩阵的一行，即构成了一个q×p的“网格-车辆”矩阵F，表示如下

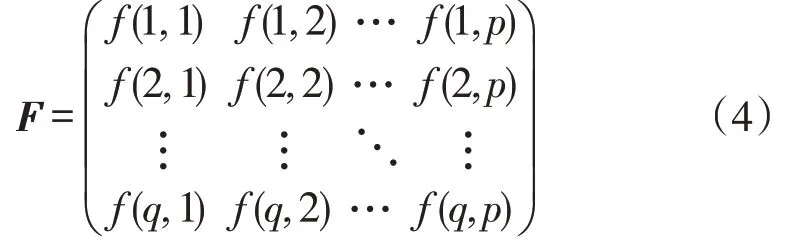
1.4 网格热度矩阵

矩阵F的元素赋值为该车辆停留在对应网格超过0.5 h的有效次数（在该网格停留少于0.5 h无法充电，视为无效通过，记为0），则可网格热度矩阵E，表示为

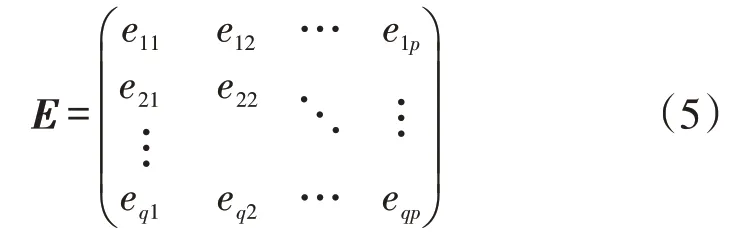
由式（5）可知，矩阵E是一个高度稀疏矩阵，对矩阵E进行语义空间相关性分析，能够实现空间网格基于电动汽车行驶热度的快速聚类。

2 电动汽车行驶轨迹与充电站的谱聚类分析

2.1 电动汽车行驶轨迹的谱聚类分析

电动汽车行驶轨迹数据是由空间位置与时间信息组成的一系列时间数据。轨迹数据间的相似度表示它们在时间与空间维度上的接近程度。为更好地研究电动汽车行驶路径间的关联性，本文应用一种路径数据相似性度量方法，结合语义空间欧氏距离［9］和其高斯核函数进行聚类处理［10］。

奇异值分解能够有效提取上下文语义信息，通过对矩阵E进行奇异值分解，生成一个由若干左奇异正交向量构成的语义空间，该空间隐含了驾驶人员对各地点的兴趣情况，其感兴趣程度由空间的特征向量与对应的奇异值内积得到。

根据奇异值分解定理，设矩阵E是m×n阶的矩阵，存在n阶正交矩阵M={m1,m2,…,ms}和N={n1,n2,…,ns}，使得

式中：λi为矩阵E的奇异值；EE′的特征向量为M的列向量；E′E的特征向量为N的列向量；s为矩阵E的秩。

将矩阵E进行奇异值分解，得到左奇异向量矩阵，即反映空间网格间上下文语义的信息空间，反映原始信号的是其语义信息空间前面的l个分量信号（l的大小由具体矩阵分解后的奇异值决定），表示如下

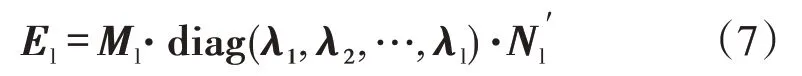
式中：左奇异向量Ml为降维语义子空间。维数l的选取影响算法的性能，若第l+1个奇异值与前l个相比，下降速度明显减小，则表示l值可选。在降维子空间内，城市网格语义空间主要代表网格间的共性信息，因此，加权语义子空间可表示为降维语义子空间的列向量与其对应奇异值的乘积，表示如下

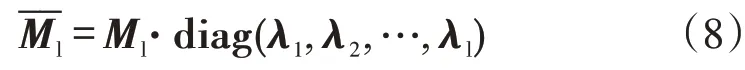
2.2 充电站的谱聚类分析

城市区域网格间的相关性可以通过语义相似图来表示，首先，将空间网格看成图的顶点，连接所有网格构成整体语义相似图。然后，给定空间数据集{b1,b2,…,bn}并定义任意网格间的语义相似度为hi,j，构建拉普拉斯矩阵，根据谱聚类算法计算拉氏矩阵特征值及特征向量。最后，对所得特征值数据聚类。具体流程如下：

（1）构建电动汽车行驶轨迹语义空间。根据上述所得的基于电动汽车大规模轨迹数据的矩阵E，进行矩阵奇异值分解，选择行驶轨迹语义空间中的前l个向量来表示空间中的大部分共性信息，通过内积建立能够反映城市空间内网格的潜在语义信息的加权语义子空间。

（2）建立城市空间网格语义距离矩阵。采用欧氏距离估计各个空间网格间的语义距离关系，生成对称的空间网格语义距离矩阵G如下

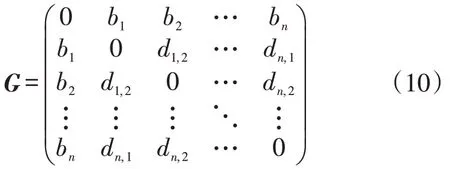
式中：di,j为两个网格bi与bj间的欧式距离。

（3）建立城市空间网格语义相似度矩阵。根据语义距离矩阵G，本文利用高斯核函数（Gaussian kernel function）进行相似性度量［11］，考虑到高斯核函数具有良好的收敛性，因而构造具有对称性的空间网格语义相似度矩阵H，矩阵元素如下

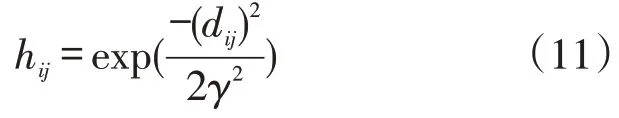
式中：hij为空间网格语义相似度矩阵元素；dij为语义空间欧氏距离，欧氏距离越大，对应网格之间的相似度越小；γ为核函数的带宽参数，用于表示网格语义相似度减小的速度，γ越大，语义相似度下降速度越慢，对应函数曲线趋于平滑。

（4）建立拉普拉斯矩阵。本节利用拉普拉斯矩阵表示城市空间网格的图谱特性［12］。根据图谱论，如果两个图的拉普拉斯矩阵具有相同的特征集，则说明图谱具有相似性［13］。本文通过分析特征多项式、特征值以及特征向量来研究图的性质，建立语义相似度矩阵H，进而建立无向图的拉氏矩阵J如下

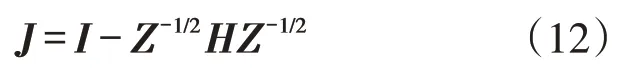
式中：I为单位矩阵；Z为对角矩阵；H表示图中每个顶点及其所连接顶点之间的相互关联程度，且满足以下关系

式中：zij为对角矩阵。

当代雕塑除了在造型上追求视觉张力，且在材料的运用方面也考虑到与作品精神内涵之关系。展示在沙漠中的这些雕塑，采用了多种材料，有GPC、不锈钢、碳钢板、铸铁、铸铜、石材、水泥等，显现出一种与主题相得益彰的审美效能。因为从当代艺术的表现手法上来讲，材料本身就具有表现性，本身就是一种表现语言，甚至是一种具有独立表现意义的视觉手段。所以，当这些中外艺术家的雕塑分布于这茫茫大漠之中时，雕塑艺术那种特有的构造形态和视觉侵袭性就会在这实体占有中，借助材料的表现力和巨大的体量，展示出一种前所未有的大漠景观，洋溢出一种特殊的场域气息！

（5）网格谱聚类。利用谱聚类算法计算出矩阵J的特征值及其特征向量，并选取前u个最小特征值所对应的特征向量，构建矩阵K，通过l均值聚类算法，对矩阵K行向量构成的数据集聚合成t类。

3 充电站的经济性分析与落点优化

3.1 充电站的经济性分析

本文进行充电站经济性分析时，只考虑电动汽车充电站的投资建设和运行维护成本，忽略充电站运行对配电网所造成的网络损耗、配电网新建馈线等方面成本。充电站的经济性主要包括年度建设成本、年度运维护成本和年度折旧成本。建设成本主要包括配电变压器、土地成本、充电机等投资成本。年度运维成本主要包括人工成本、设备维修成本等。电动汽车充电站的年度总成本可以表示为

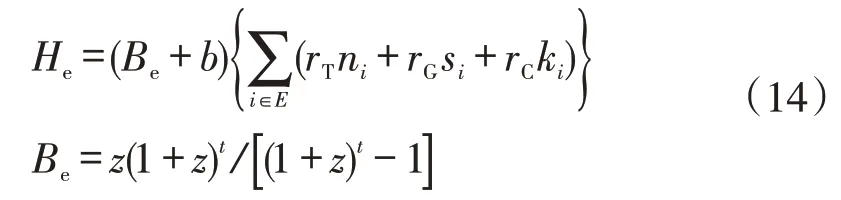
式中：He为电动汽车充电站的年度总成本；Be为充电站年等值投资回收系数；b为每年折算系数，本文设为10%；E为待建充电站集合；rT和ni分别为充电站中变压器的单价和数量；rG和si分别为充电站的土地价格及占地面积；rC和ki分别为充电站中充电机的单价和数量；z为贴现率；t为投运年限，本文设为20 a。

3.2 充电站的落点优化

本文基于谱聚类分析的应用，考虑充电站的运行经济性。首先，获取电动汽车行驶数据，建立数据集；其次，采用聚类算法，进行电动汽车空间语义聚类分析，并依照聚类结果，按优先级确定候选充电站位置；然后，在相同聚类中，以经济最优为目标，在上述聚类结果中将候选站位置进行进一步的优先级排序；最后，根据聚类分析和经济性评价的结果，确定充电站的落点位置。

4 算例分析

4.1 分析区域处理

设定某城市面积约为120 km2，共有1 000辆电动汽车，每辆电动汽车可以在城市范围内随意行驶，且可以不限时间在任意地点内停留。现将城市空间中网格大小设置为200×200 m2，共有3 000个空间网格数。城市区域内按功能划分，分别设立4个旅游区、4个学校区、4个医院区、4个购物区、若干家庭区域和工作区域。

借鉴文献［14］提出的基于概率模型的运动趋势查询及处理方法，建立电动汽车的落点概率模型，计算在未来时刻可能出现的位置以及出现的有效次数。仿真计算电动汽车在3 000个网格区域内经过与停留的次数和时间，将收集的电动汽车的行驶数据作为本次实验的原始大数据样本。为了与实际情况接近，设定电动汽车在一天中的6:00—18:00时间段内100%车辆出行，18:00—24:00时间段内有80%车辆出行，24:00—次日6:00时间段内有20%车辆出行。设定电动汽车的有效充电时间为30 min，则有效数据为停留在同一网格中大于30 min的电动汽车。由交通拥堵原因导致的停留超过30 min的电动汽车占比率极少，所以此类情况在此忽略不计。本文设置的城市区域图如图1所示。

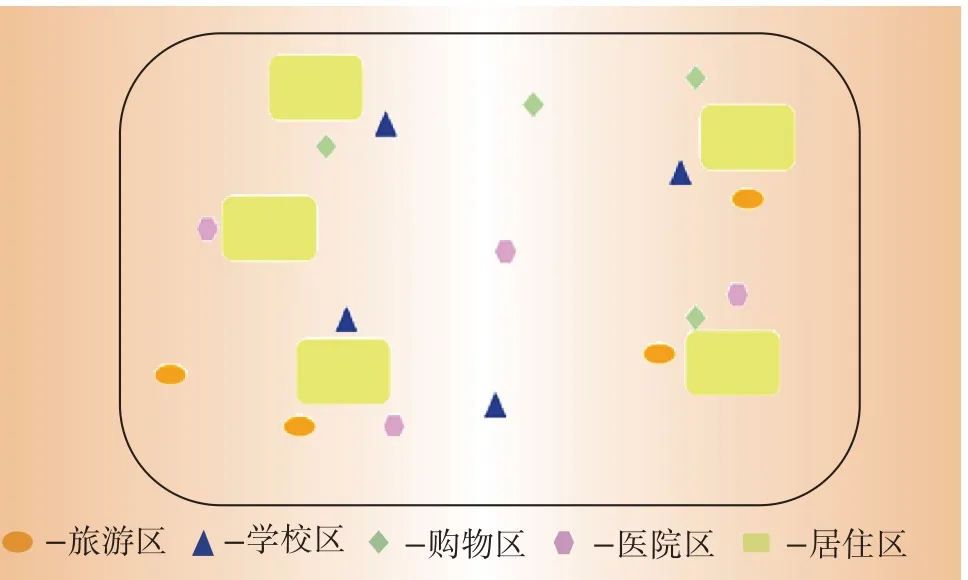
图1 城市区域Fig.1 Urban area

4.2 充电站规划数据处理

该部分计算主要以分析在城市规划空间边界内车辆行驶数据为依据，基于车辆行驶数据，对充电站规划位置进行排序，为工程实际需求提供科学参考。

4.2.1 行驶数据处理

空间聚类结果如表1所示，表中包含48 h之内经过网格车辆的总次数和有效经过次数、单个网格经过车辆的最大次数、最小次数以及对应区域的实际物理含义等信息。

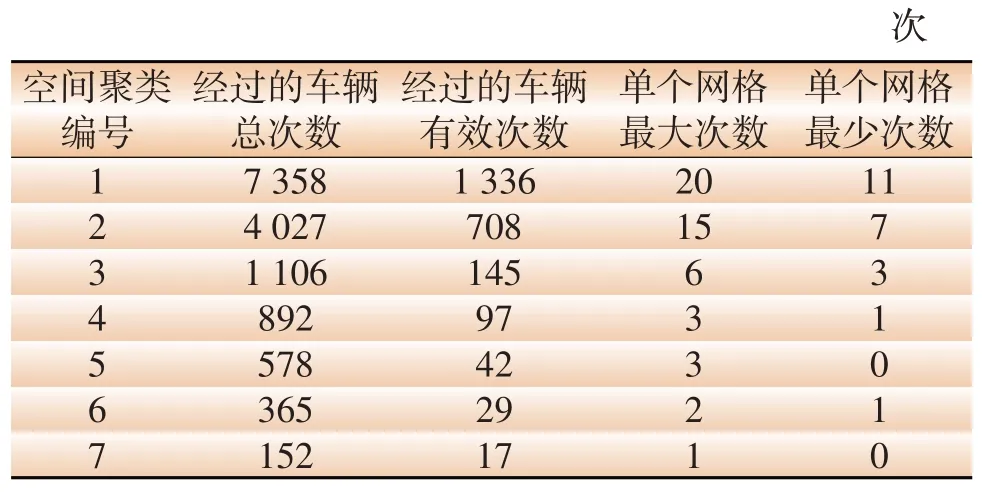
表1 空间区域聚类结果Table 1 Cluster results in planning area

表1的结果反映了车辆在不同网格中的热度，显示了轨迹各网格间的强相关性。由表1可知，不同网格的聚类与实际物理地点的热度基本相同，符合电动汽车日常行驶习惯。空间网格聚类1的部分网格描述如图2所示。

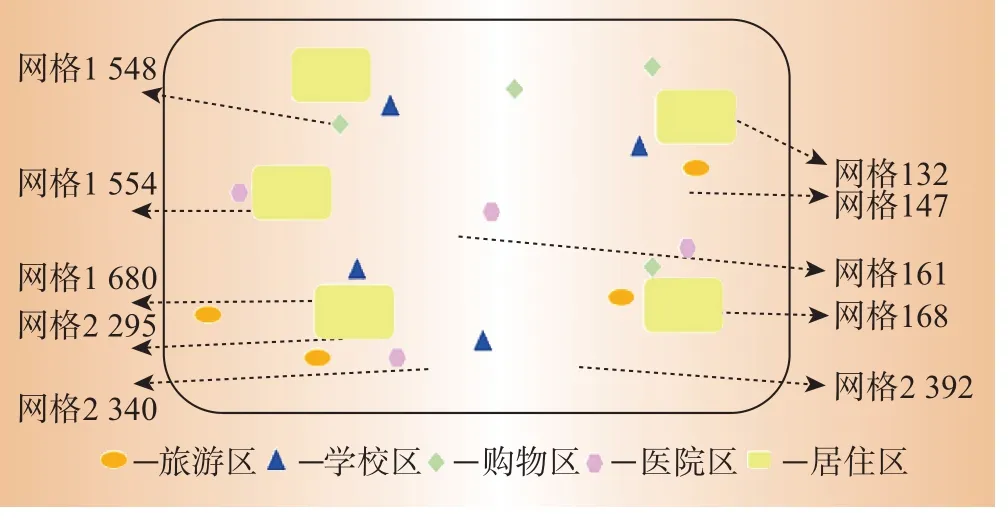
图2 空间网格聚类1结果Figure 2 Results of cluster 1 in spatial grid

电动汽车在不同网格中停留次数的部分统计数据如图3所示。

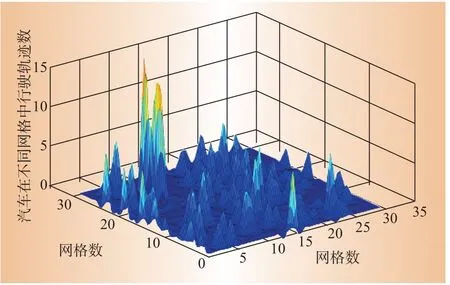
图3 车辆行驶的部分统计数据Fig.3 Part of statistics of electric taxi trajectory

对比图2的聚类结果和图3的车辆行驶轨迹数据可知，本文提出的聚类结果与实际城市空间的行驶热度大致吻合。实际情况中，车辆每天的行驶轨迹是随时变化的，所以仅按照上述电动汽车行驶轨迹的统计结果，会造成轨迹语义空间信息的不稳定，不能正确全面反映电动汽车的有效聚类。所以在处理数据时，对于某些距离较近但热度差距较大的网格，由于行驶轨迹具有相关性，也被聚合到同一聚类中。所以聚类结果不完全根据行驶轨迹热度，体现了车辆行驶轨迹在网格间的较强相关性。按此思路所得聚类结果较单独轨迹数据所得聚类结果更为丰富全面。

4.2.2 充电站经济性分析

在相同聚类中，选择不同的地理位置，在经济性上会给建设充电站带来较大差异。不同网格建设充电站的花费不同，表1中的聚类1中在不同网格建设充电站所需成本一览表如表2所示。

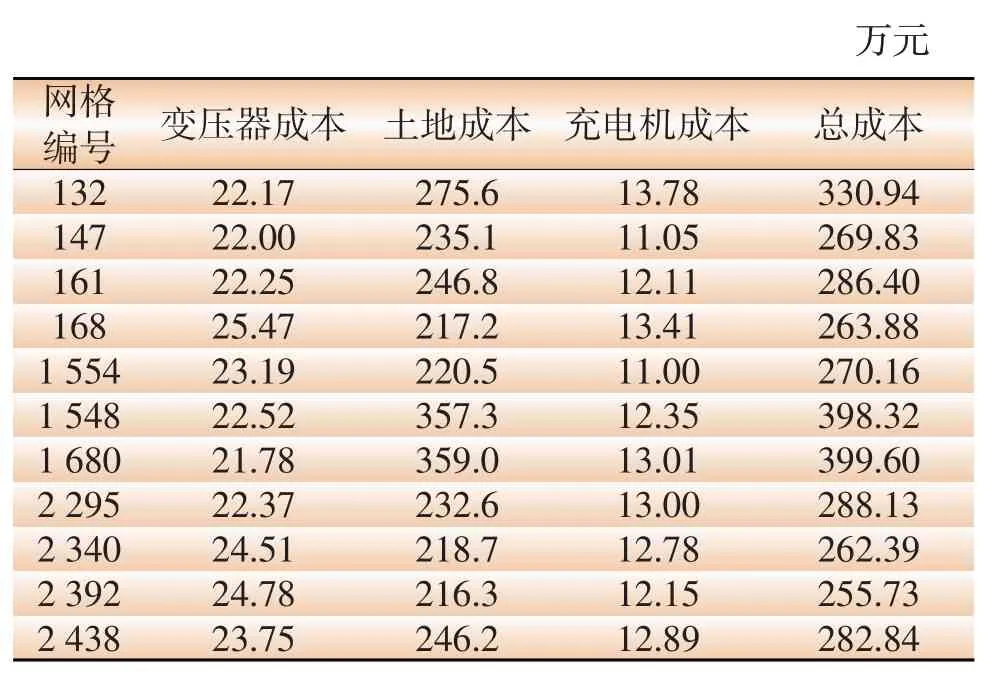
表2 充电站建设成本一览表Table 2 Cost of charging station construction

由表2可知，在聚类1中，各充电站规划建设成本是不同的。其中，网格2 392中的总成本最小，最为经济；网格1 548和网格1 680的综合成本较高，经济性较差；选取网格2 392作为电动汽车充电站站址最为合适。同时也可看出充电站建设总成本受地域影响较大，在满足用户使用与出行便捷的基础上，经济成本也是充电站选址的重要参考因素。