基于Motif 聚集系数与时序划分的高阶链接预测方法∗

康驻关,金福生,王国仁

(北京理工大学 计算机学院,北京 100081)

网络中的链接预测[1]指通过已知的网络结构信息,预测网络中尚未产生链接的节点间产生新链接的可能性.如果给定网络的当前状态,则链接预测将重点放在评估未来状态中存在边的可能性.可以理解为预测社交网络中两个人未来相互认识,计算机网络中的通信或生物网络中的生物分子相互作用的可能性.一个好的链接预测算法不仅可以用来挖掘网络中节点与结构间的关系,而且可以进一步帮助研究者探索网络结构的演化规律.目前,链接预测不仅在理论研究上取得了较好的成果,而且在一些特定的场景下也具有广泛的应用价值,例如预测社交网络中的友谊发现、推断基因与疾病之间的新关系、发现学术界的合作关系等[2,3,4]具体应用.常见的链接预测算法一次只需要预测一条边,然而在分析复杂网络结构演化时往往需要考虑所有的边,这些算法则不能进行很好的扩展.本文提出的高阶链接预测任务将探测更大的特征集,这也要求算法能够捕获数据集中更多潜在的可表示性特征.原则上,好的链接预测模型可以适用于网络中任意结构的预测,具体表示为预测网络中任意高阶的交互.毋庸置疑,链接预测是复杂的网络分析中一个有重要实用价值的研究问题,在交互事件发生之前对其进行预测,是深入探索网络结构演化的一项重要能力.

目前,绝大多数的链接预测算法都是基于网络低阶结构的研究[1,5],这些方法通常只分析了网络中成对节点间的关系,无法有效捕获高阶结构中的潜在联系,从而在高阶结构中的预测效果表现较差.本文使用网络高阶结构来进行链接预测,充分挖掘网络中高阶结构的演变信息,从而获得对复杂网络结构的新见解.为了简化研究和便捷可表示性,本文重点以高阶结构中的基础结构(无向三角形结构)为主要的研究对象.

为了解决上述提出的高阶特征表示问题,本文从高阶网络结构特性和网络结构演化两个维度进行深入分析,提出了计算高阶结构聚集性特征和网络结构演变特征的两个方法:首先,通过对高阶结构的聚集行为研究,将其进行量化用来表示高阶结构的聚集程度,从而有效捕获高阶结构的聚集性特征;其次,通过将数据集进行切割分片,分析随着时间演变网络结构的变化规律,提出节点间链接频次和链接趋势等具有网络结构演变特性的特征,有效利用了动态网络演化的历史信息.基于上述两个方法,提出了基于Motif 聚集系数与时序划分的高阶链接预测模型用于完成预测任务.

综上所述,本文主要贡献总结如下:

(1)通过分析网络高阶结构,提出Motif 聚集系数特征,将传统对单节点的聚集系数定义扩展到高阶结构的聚集系数定义.经过实验验证,Motif 聚集系数可以有效捕获网络中高阶结构的聚类信息,并且验证了使用Motif 聚集系数表示高阶结构聚集程度的有效性;

(2)通过分析网络结构演变的特性,提出节点间链接频率和链接趋势等表示网络结构演变的重要特征,可以挖掘网络结构演变过程中节点之间的链接变化规律;

(3)提出了基于Motif 聚集系数与时序划分的高阶链接预测模型(high-order link prediction model based on Motif aggregation coefficient and time series division,简称MTLP),有效融合传统链接预测提出的相似性度量特征与本文提出的Motif 聚集系数特征和表示网络结构演变的特征,通过使用多层感知器网络(multi-layer perceptron,简称MLP)算法完成高阶链接预测任务.

本文在第1 节介绍相关研究工作.第2 节给出本文的问题定义.第3 节重点介绍本文提出的高阶链接预测模型.第4 节为实验分析.第5 节总结全文.

1 相关研究

近年来,链接预测方法主要应用在社交网络和其他复杂网络等领域.针对现有的链接预测算法的研究,本文将其预测模型大致分为基于局部结构相似性的链接预测方法、基于概率模型的链接预测方法和基于机器学习的链接预测方法这三大类.

(1)基于局部结构相似性的链接预测方法

常见的相似性指标有基于调和平均数、几何平均数和算术平均数相似性指标[3]、基于共同邻居(common neighbors,简称CN)相似性指标[1,6]、基于Jaccard 相似性指标[1]、基于Adamic/Adar(Adamic-Adar,简称AA)相似性指标[1,7]、基于优先链接(preferential attachment,简称PA)相似性指标[1,6,8]、基于Katz 相似性指标[1,9,10]、基于PageRank 相似性指标[1,11,12]和基于层次化混合特征指标[13]等.基于局部结构相似性的方法主要是用于捕获局部网络的特征,从而根据相似性的特征进行链接预测.但是这些方法无法有效地捕获高阶结构的特征,仅适用于低阶的链接预测.如果将其扩展到高阶链接预测,其预测效果并不理想.

(2)基于概率模型的链接预测方法

Clauset 等人[14]最初提出基于最大似然估计的链接预测方法,将其应用到有明显层次的网络结构中,发现有比较高的精确度;Tian 等人[15]提出了一种基于最大似然估计的链接预测模型,将脑网络的数据建立了层次随机图,再结合马尔可夫算法计算脑网络边的链接概率,显示出了良好的预测性能.Das 等人[16]提出一种基于随机马尔科夫链预测模型,其以时序图作为社交网络链接预测的基础.Liu 等人[17]提出一种基于动态博弈的双向选择机制来预测未来的网络拓扑结构.该类方法适合于在静态网络下进行预测,但是动态网络的结构是频繁变化的网络,因此该类方法往往难以满足要求.

(3)基于机器学习的链接预测方法

Chiu 等人[18]提出了弱估计器的特征指标,该特征重点考虑了随着时间推移而发展的网络中链接预测的相关趋势,并将该指标作为构建深度神经网络的有效特征向量进行学习.Yaghi 等人[19]通过提取网络中节点度中心性(DC)和紧密度中心性(CC)两个特征来增强给定边的重要性,并使用机器学习模型进行链接预测.Abuoda 等人[20]进一步对网络拓扑结构进行分析,并提出网络模式(Motif)结构应用于链接预测.Chen 等人[21]提出了一种基于图卷积网络(GCN)的嵌入式长短期记忆网络(LSTM),用于端到端动态链接预测.该类方法在结构相似性链接预测方法的基础之上进一步获取网络特征,使用机器学习模型进行训练学习完成链接预测任务.但是多数的研究仅仅是更改已有的机器学习模型,缺乏对高阶网络结构中存在的特性和网络结构演变信息进一步的分析,以至于达不到预期的预测效果.

虽然当前的链接预测算法有很多,但面对上述各种链接预测的研究仍存在不足.一方面,现有的大多数链接预测算法只考虑了网络中很少一部分的局部结构特征,这些算法基本上都是从节点相似性角度进行度量.例如计算共同邻居、余弦相似性等局部结构特征,这些特征往往仅适用于节点对之间的相似性度量,但是在一些复杂的网络中,高阶结构间的特性远不止如此.另一方面,现有的链接预测算法很少考虑网络中的时序信息,以及随着时间推移网络不断变化的信息.尽管一些学者尝试使用长短期记忆网络(LSTM)解决网络结构演化过程中的时间依赖性问题,但是无法具体地分析网络演化规律,缺乏对表示时序信息的特征做出进一步解释.

本文提出的链接预测算法与上述算法不同之处如下.

(1)传统的链接预测算法主要提取网络低阶结构之间的相似性特征,而忽略高阶结构中存在的特征;本文通过研究高阶结构的特征来获得对网络高阶结构的新见解.本文提出了Motif 聚集系数的方法,通过计算网络高阶结构的Motif 聚集系数来捕获高阶结构中存在的聚类信息,从而丰富网络结构的特征;

(2)当前,一些算法使用LSTM 模型解决网络结构演化过程中的时间依赖性问题,但是无法区分网络中哪些表示网络结构演变的特征在预测任务中起到决定性作用,缺乏对网络结构演化规律的有效分析;本文重点在于分析网络中存在的可表示性特征,因此本文通过对动态网络进行分析,发现节点间的链接频率和链接趋势等表示网络结构演变的重要特征,可以更加细致地解释网络结构变化信息.

2 问题定义

本文研究的重点是预测多个节点间产生链接形成高阶结构,因此我们通过研究三角形结构来确定高阶链接预测的模式.为了使读者更容易理解本文的研究内容,本节先介绍几个相关概念,针对高阶链接预测任务进行形式化定义.

定义1(单形).单形表示一个包含k个节点的集合,每个单形对应一个时间戳,具体表示为,|Si|=k,我们称Si为单形,ti为该单形对应的时间戳.

定义2(闭合三角形).如果有3 个节点存在于同一个单形,例如{u,v,w}⊂Si,则这3 个节点形成一个闭合三角形,具体可表示为组成闭合三角形的3 个节点至少同时出现在一个单形中的情况.

定义3(开放三角形).如果3 个节点中的任意一对节点至少同时出现在一个单形中,但不存在某个单形同时包含这3 个节点,我们称这3 个节点形成一个开放三角形.

定义4(简单闭合事件).在t时刻之前,节点间可以任意的产生链接,但是没有任何一个单形同时包含{u,v,w}这3 个节点,如果在t时刻之后存在一个单形同时包含了这3 个节点,则该过程称为简单闭合事件.

定义5(高阶链接预测).为了简化表示,本文将高阶链接预测定义为预测节点三元组上的简单闭合事件.简单来说,我们研究的高阶链接预测问题是预测哪些尚未同时出现在同一个单形中的3 个节点将来会同时出现在某一个单形中,具体表示为预测哪些开放三角形在未来会经历简单闭合事件.

3 基于Motif 聚集系数与时序划分的高阶链接预测模型

为了充分利用并整合动态网络中高阶结构特征与结构演变特征,以提高链接预测模型的性能,本文提出一种基于Motif 聚集系数与时序划分的高阶链接预测模型(MTLP).本节首先介绍该模型的基本思想,然后分别介绍Motif 聚集系数与网络结构演变特征的计算方法,最后给出基于多层感知器网络的链接预测算法实现.

3.1 MTLP模型的基本思想

本文通过构建MTLP 模型来完成预测任务,该模型主要由3 部分组成,分别是提取网络高阶结构Motif 聚集系数特征、提取网络结构演化特征和构建基于MLP 的链接预测算法,模型的整体框架如图1 所示.

Fig.1 MTLP model framework图1 MTLP 模型框架图

(1)聚集系数是网络科学中数据建模的重要统计数据[22,23,24],也是机器学习中非常有用的特征,例如在角色发现[25]和异常检测[26]中的应用.但是传统聚集系数本身具有限制条件,因为它仅限于测量一个简单楔形结构的闭合概率,本质上表示网络中单个节点的聚集程度,无法表示网络中高阶结构的聚集特性.本文重点研究基于高阶结构的链接预测任务,而传统的局部聚集系数并不适用于表示高阶结构的聚集行为.因此,将测量单个节点的局部聚集系数扩展至测量高阶结构的聚集系数,是提取Motif 聚集系数特征模块主要解决的问题;

(2)链接预测的相关方法,本质上都是利用网络历史信息并将其压缩为一个网络,以预测下一时刻的网络.可以说,目前大多数的链接预测都是基于网络快照的方法,例如在给定的时间内分析给定的网络快照,用于下次链接预测.但是这些方法仅考虑了前一时刻的网络拓扑结构信息,而与前一时刻网络的动态发展无关.因此,通过对动态网络进行分析并捕获网络结构演变信息,是提取网络结构演化特征模块主要解决的问题;

(3)本文研究的问题是预测一个三角形是否会经历简单闭合事件,该问题实际上是二分类问题.因此,本文使用MLP 算法来完成链接预测任务.

3.2 提取Motif聚集系数特征

聚集系数[22,23,24]是用来量化网络中节点聚集程度的度量标准.本文扩展了传统的局部聚集系数,将单个节点的聚集系数扩展为高阶结构的聚集系数,用来衡量网络中高阶结构的聚集程度,即Motif 聚集系数.

本文主要研究的是无向图网络,定义G=(V,E)表示无向图,n=|V|表示无向图中的总节点数,m=|E|表示无向图中的总边数,任意节点u的邻居节点集合为N(u).定义Cmotif(g)为Motif 聚集系数,g表示任意高阶结构,Gtotal(g)表示g的全局聚集系数,N(g)表示g中所有节点的共同邻居节点,|Wi,j|表示节点i与节点j之间是否存在链接:如果存在,则|Wi,j|=1;否则|Wi,j|=0.Motif 聚集系数的公式定义如下:

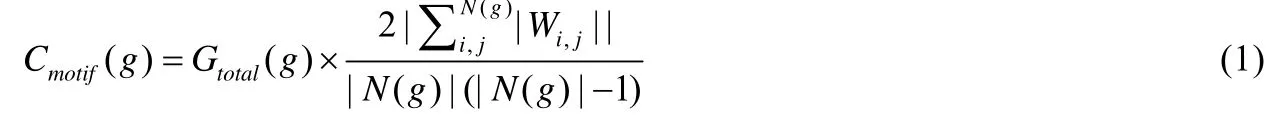
通过上述的定义已经了解到如何计算Motif 聚集系数,计算Motif 聚集系数首先需要计算每个子图的全局聚集系数,再计算子图中每个高阶结构的共同邻居,从而得到最终结果.从公式上来看,直接进行计算的代价非常昂贵,因此,我们对算法进行了优化,通过维护一个集合用来存储每个节点的邻居节点,使时间复杂度降为o(n),极大地缩短了计算Motif 聚集系数的时间,计算高阶结构的Motif 聚集系数算法详见算法1.

算法1.计算Motif 聚集系数.

Input:高阶结构g,邻居节点集合N;

Output:Cmotif(g)(高阶结构g的Motif 聚集系数).

1 算法CalculateMotifCluf(g,N)

2 定义triNum记录g中闭合三角形的个数,Gtotal(g)记录全局聚集系数

3 定义tempNum用于临时计数,定义conns用于记录共同邻居中相互链接的边数

4 forg中的任意3 个节点(i,j,k)do

5 if (i,j,k)任意两个节点间存在链接 then

6triNum++

7 end if

8 end for

9 forg中的任意一个节点ido

10tempNum+=

11 end for

13 forN(g)中的任意两个节点(i,j)do

14 if (i,j)两个节点间存在链接 do

15conns++

16 end if

17 end for

19 returnCmotif(g)

3.3 提取网络结构演变特征

网络演化的历史为理论上的预测提供了更多信息,同时也为网络分析增加了一个全新的维度.我们采用图序列来描述网络的动态变化,并分析随着时间的推移,节点结构之间关联性的演变过程.

首先在数据预处理部分,我们将网络切分成表示一系列图序列的时间片集合G=(G1,G2,…,Gt−1,Gt),其中,Gt=(Vt,Et)表示第t个时间序列的网络图,每个网络图对应一个邻接矩阵Wt.动态网络的拓扑结构会随着时间t的变化而不同,主要是随着时间的变化,节点间的链接产生了不同的变化,有的节点间添加新的链接,有的节点间删除原有的链接,在不同的时间序列中,节点对之间的链接关系也会不同.每个时间片中节点间的链接变化如图2所示,其中,虚线表示图中节点从G1时刻演变到G2时刻的映射.

Fig.2 Representation of node link changes in different time slices图2 不同时间片中节点链接变化表示

由图2 可知:网络中的结构会随着时间推移产生不同的变化,这些变化会在每个时间片中留下一系列的痕迹.本文主要从简单闭合事件的生命周期转换进行分析,通过考虑一系列时间序列的转换来分析节点间的结构转换关系是否能够对未来形成闭合三角形有重要的影响.通过分析发现:在大多数的数据集中,许多新形成的单形由k个节点组成,这些节点出现在同一个单形中之前也分布在不同的单形中,与其他节点产生交互.因此,本文认为,网络中产生开放三角形的一个可能假设是链接创建中的时间异步性.例如,开放三角形中的节点不能同时出现在同一个单形中,这些节点只能在不同时间段进行交互形成链接.不管开放三角形是如何创建的,随着网络的发展,这3 个相关的节点在未来都可能在同一个单形中同时出现.通过对三角形经历简单闭合事件过程分析,每一种结构的变化对未来是否能够形成闭合三角形有着重要影响.因此,本文将整个结构演变过程进行时间上的划分,分别统计每个时间片中的局部结构关系,从而在时序维度提取重要的特征信息,主要提取了节点间链接频次和链接趋势两项特征用来表示网络结构变化规律.

在网络演化的进程中,不同节点间的链接频次各有不同.统计链接频次可以表示节点间的动态联系,因此,本文将链接频次作为动态网络中的一个重要特征.定义fsn(i,j,k)为n个时间片中三角形的eij,eik,ejk这3 条边的链接频次算数和,其中,表示第t个时间片中节点i与节点j之间是否存在链接:如果存在,;否则,.节点间的链接频次公式定义如下:

网络结构在演化时呈现不同的链接规律,这些规律既具有确定性又具有不确定性,因此,可以将每条边的链接趋势作为一项重要的链接指示特征进行归纳.定义表示第t个时间片与相邻时间片中三角形边数的链接趋势,链接趋势减少为−1,链接趋势不变为0,链接趋势增长为1.本文将数据切割成n个时间片,通过计算n个时间片中三角形3 条边的链接趋势的算数平均值,作为节点间链接变化的最终链接趋势,节点间的链接趋势公式定义如下:

节点间的链接频次和链接趋势可以有效地捕捉到动态网络演化规律,同时,这些特征也可以通过简单的计算将其表示出来.因此,本文将在后续的链接预测模型中使用这些可表示网络结构演变的特征,从而有效捕获网络演变信息.

3.4 构建基于MLP的链接预测算法

本节主要介绍构建基于MLP 的链接预测算法,用于完成高阶链接预测任务,算法流程图如图3 所示.

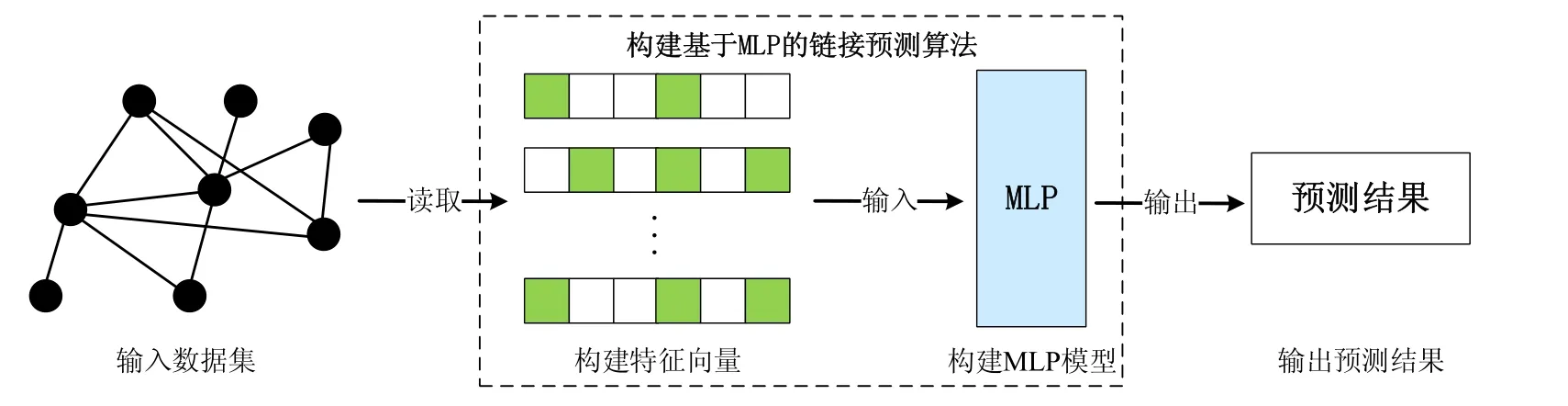
Fig.3 Flow chart of constructing MLP-based link prediction algorithm图3 构建基于MLP 的链接预测算法流程图

3.4.1 构建特征向量

在机器学习领域,只有数据和特征才能决定机器学习的上限,一个优秀的模型和算法只能不断地逼近这个上限.因此,选择具有代表性的特征也是一项非常重要的工作.通过前文的分析,本文已经提取出动态网络中Motif 聚集系数特征和网络结构演变相关特征.除此之外,我们也加入了一些传统链接预测经常使用的特征,例如节点的邻居和节点的度等相似性特征,通过融合这些特征构,建成可供机器学习模型训练的特征向量.特征向量构建算法详见算法2.

算法2.构建特征向量.

Input:单形Si列表,时间列表ti,切割次数n;

Output:特征向量LS.

这些特征主要分为3 类:第1 类为大多数链接预测算法所考虑的网络拓扑结构相似性特征,例如节点的度以及节点的邻居等;第2 类为高阶结构特征,例如高阶Motif 聚集系数,该特征有效捕获了高阶结构的聚集特性;第3 类为网络演变过程中可表示结构变化的特征,例如节点间的链接频次和链接趋势等.这些特征都存在于现实网络中,可以有效地表示网络结构间的关系.

3.4.2 构建链接预测模型

针对链接预测问题,本文选用多层感知器(MLP)网络完成预测任务,MLP 算法自从被提出以来,主要被应用于节点分类等有监督学习任务.该算法的核心是训练学习函数f(X):Rm→Rn,其中,m是输入的维数,n是输出的维数.具体表示为:给定一组特征向量特征x和标签y,它可以学习用于回归或分类的非线性函数.

图4 列举了一个具有标量输出的单隐藏层MLP 模型:模型最左边一组代表输入特征的神经元构成输入层;模型中间多个有向层中分布的神经元构成整个隐藏层,每个隐藏层中的神经元将前一层的值进行加权线性求和转换,再使用非线性激活函数进行计算得到该神经元的输入数据;模型最右边为输出层,主要用于接收由最后一个隐藏层经过变换计算输出的值.

Fig.4 Single hidden layer MLP图4 单隐藏层MLP

MLP 模型具体用法是:给定一组训练样本(x1,y1),(x2,y2),…,(xn,yn),其中,xi∈Rn,yi∈{0,1},则单隐藏层 MLP模型学习到的函数为f(x):

其中,W1∈Rm和W2,b1,b2∈R是模型参数.W1,W2分别是输入层与隐藏层之间和隐藏层与输出层之间的权重,b1,b2分别是隐藏层和输出层的偏置值,g(x)是激活函数.本文使用的激活函数为双曲正切函数,计算公式如下:

对于二分类问题,f(x)通过logistic 函数能够得到0～1 之间的输出值.若将阈值设置为0.5,则输出大于等于0.5 的样本分到正类(positive class),其他情况分为负类(negative class).同时,一般情况下,MLP

算法会根据不同问题使用不同的损失函数.本文的高阶链接预测为二分类问题,因此采用交叉熵损失函数,计算公式如下:

本文使用MLP 模型的输入参数为算法2 构建的特征向量,同时采用3 个全连接的隐藏层进行计算,模型的输出为当前开放三角形是否会经历简单闭合事件的状态.MLP 模型最终输出结果为0 和1,其中,1 表示该开放三角形会经历简单闭合事件,而0 表示该开放三角形不会经历简单闭合事件.

4 实验结果与分析

本节详细介绍了数据集、实验环境、评价指标等内容.首先,对Motif 聚集系数特征和网络结构演变等特征进行了有效性验证;接着,通过与不同链接预测算法进行对比,对本文提出的MTLP 模型进行综合评价.

4.1 实验数据集

本文采用来自5 个领域的14 个数据集[27],分别是合著网络(coauth)、在线标记网络(tags)、在线参与网络(threads)、电子邮件网络(email)和近距离接触网络(contact).

每个数据集是一组带有时间戳的节点集.这些数据集分布在不同的领域,因此包含了丰富多样的结构,非常适合多种实验测试,每个数据集的详细信息见表1.

Table 1 Data set information表1 数据集信息

4.2 评价指标

本文使用ROC 曲线和AUC-PR 值[28]作为评价指标对实验结果进行度量.

ROC 是由True Postive Rate(TPR)和False Postive Rate(FPR)组成的曲线,其中,TPR 代表分类器预测的正类中实际经历简单闭合事件的正实例占所有正实例的比例,也可表示为正确预测的覆盖程度;FPR 代表分类器预测的正类中实际未经历简单闭合事件的负实例占所有负实例的比例,也可表示为预测虚报的程度.两项指标的计算公式如下:

对于链接预测模型而言,根据预测时设定的阈值,在测试样本集上会得到TPR 和FPR 的点对.如果遍历全部阈值,就可以得到多个点对,将点对连接便得到一条经过(0,0),(1,1)的曲线,这就是此链接预测模型的ROC 曲线.同时,我们当然希望虚报的越少越好,覆盖的越多越好.因此,FPR 越低,TPR 越高,ROC 曲线越接近左上角,意味着预测模型的性能越好.

由于很多时候ROC 曲线并不能明确地指出哪个分类器的效果更好,而AUC-PR 指标具有明确的数值,对应AUC-PR 值越大的分类器效果越好,因此本文也使用AUC-PR 值作为评价模型性能的标准.同时,AUC-PR 适用于类不平衡的预测问题,我们的数据集就是这种情况,因此该指标可以充分地对比不同模型的性能.

同时,本文使用随机分数作为基准,该分数为测试集中经历简单闭合事件的三角形个数与训练集中开放三角形个数的比例.随机分数以绝对值列出,通过比较每个模型的AUC-PR 与基准的相对值来衡量不同模型的性能,分值越大,则表示模型的性能越好.

4.3 验证特征有效性

本节主要验证Motif 聚集系数特征和网络结构演变相关特征的有效性,主要是从Motif 聚集系数特征和网络结构演变特征两个维度对数据进行系统域划分,通过训练一个多项式逻辑回归模型来确定不同数据集的系统域.

本文采用scikit-learn 库中的多项式逻辑回归模型进行训练学习,训练的特征向量包含开放三角形的比例、开放三角形的平均Motif 聚集系数和开放三角形的网络结构演变这3 项特征和一个截距项.为了防止模型过拟合,采用l2正则化进行约束,最终训练出一个多项式逻辑回归分类器来预测划分的系统域.为了直观地表示出系统域的划分,在这里给出一个使用开放三角形比例和开放三角形的平均Motif 聚集系数作为协变量训练出的系统域划分图.从图5 上可以观察到:本文提出的Motif 聚集系数可以很好地将不同的数据集划分到各自的领域,从而体现出Motif 聚集系数可以作为网络中高阶结构的一项重要的特征.

Fig.5 System domain division diagram图5 系统域划分图

为了更精准地验证本文提出的特征有效性,我们采用消融实验,分别控制平均Motif 聚集系数特征和网络结构演变特征这两个变量进行实验,用于验证系统域划分的准确性,实验结果见表2.

Table 2 Comparison of accuracy of different features表2 不同特征准确率对比

从表2 可以看出,任意添加一项平均Motif 聚集系数特征或者网络结构演变特征都可以提高数据域划分的准确性.尽管最终划分数据域的结果并不完美,但是已经可以说明本文提出的Motif 聚集系数与网络结构演变相关特征的有效性.

4.4 不同链接预测算法性能对比

4.4.1 对比方法

本文选取了10 个链接预测模型用于对比实验,其中前7 个为经典的链接预测模型,后3 个为近两年最新的基于机器学习的链接模型,分别如下.

• Harm.Mean[27]是基于启发式的结合边强度指示的相似性模型,主要是通过计算三角形中3 条边对应的权值相加和的倒数,作为一项相似性指标用于链接预测;

• Geom.mean[27]是基于启发式的结合边强度指示的相似性模型,主要是通过计算三角形中3 条边对应的权值连乘积的三次方根,作为一项相似性指标用于链接预测;

• Arith.mean[27]是基于启发式的结合边强度指示的相似性模型,主要是通过计算三角形中3 条边对应的权值相加的均值,作为一项相似性指标用于链接预测;

• Adamic-Adar[1]是基于邻居节点的相似性模型,主要通过计算三角形中3 条边邻居的对数倒数和,作为一项相似性指标用于链接预测;

• Pref.Attach[1]是基于邻居节点的相似性模型,主要通过计算三角形中3 条边邻居的乘积,作为一项相似性指标用于链接预测;

• Katz similarity[1]是基于路径的相似性模型,主要通过计算三角形中3 条边的路径和,作为一项相似性指标用于链接预测;

• PPR[1]是基于路径的相似性模型,主要通过计算三角形中3 条边对应的随机游走的概率,作为一项相似性指标用于链接预测;

• Benson 等人[27]发现,连接强度和边缘密度是高阶组织链接的积极指标,并使用这些指标进行链接预测;

• Yaghi 等人[19]通过构造节点的中心性度量指标来提高预测的准确性;

• Chiu 等人[18]提出了网络链接中弱估计指标用于链接预测,从而提高预测性能.

4.4.2 对比实验

本文首先选取对比方法中前7 个经典的链接预测模型与本文提出的MTLP 模型进行对比实验,并且使用ROC 曲线来评价每个模型的性能.这些模型都是已知的模型,可在链接预测任务中提供良好的预测效果.为了验证不同模型的性能,我们选取几个典型的数据集进行对比实验,ROC 对比结果如图6 所示.

Fig.6 ROC comparison results图6 ROC 对比结果

从实验结果可以看出:本文提出的MTLP 模型在不同数据集上都表现出了较优的性能,主要表现为ROC 曲线下的面积越大,性能越优.

除了与经典的链接预测模型进行对比,我们也与近两年最新的基于深度学习的链接预测算法进行对比.为了更加详细地对比每一个模型的性能,本文同时考虑以上10 个链接预测模型,并使用随机模型分数作为基准,使用AUC-PR指标来评价每个模型的预测性能.实验结果见表3,图表中黑色加粗的数字表示在该数据集上链接预测性能最优的模型得分.

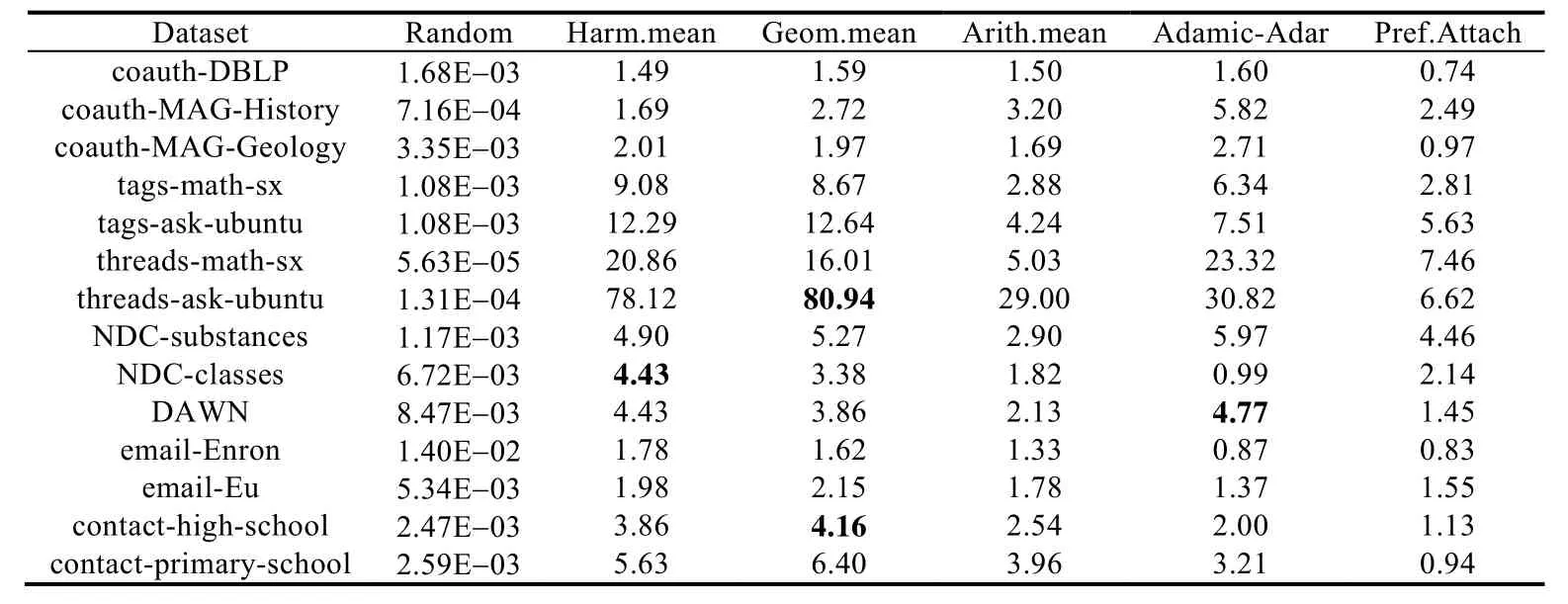
Table 3 Experimental results AUC-PR value表3 实验结果AUC-PR 值

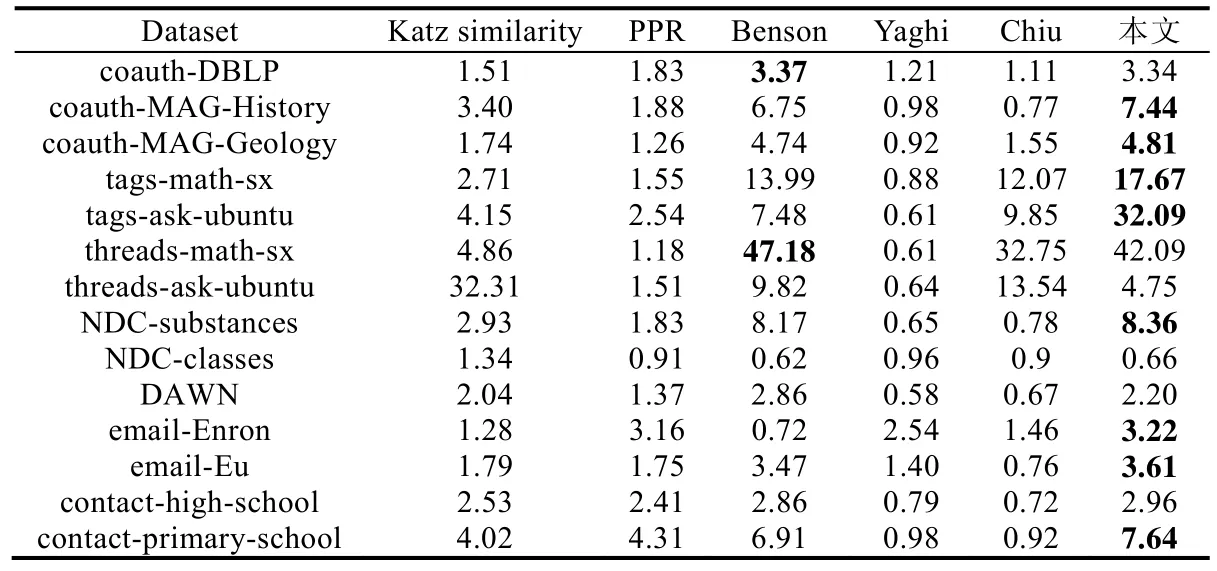
Table 3 Experimental results AUC-PR value (Continued)表3 实验结果AUC-PR 值(续)

从上面的实验结果可以清楚地看到:虽然没有任何一个模型在所有数据集上都能表现最佳,但本文提出的算法可以在大多数的数据集上表现出更好的预测性能,例如coauth-MAG-History,coauth-MAG-Geology,tagsmath-sx 和tags-ask-ubuntu 数据集.这说明本文提出的算法有效捕获了网络的聚集特性和结构演变特性,从而得到较好的实验结果.但是在一些数据集上表现的结果较差,例如threads-ask-ubuntu 数据集,我们通过对该数据集分析发现:该数据集聚集程度较低,同时开放三角形的比例也较低,如果开放三角形比例较低,会出现数据分布不均匀的现象,这是导致预测结果较差的主要原因.值得注意的是:从不同的实验结果可以看出,使用不同相似性指标的模型也可以在部分数据集上表现出了较好的结果.例如基于启发式的结合边强度指示的相似性模型在threads-ask-ubuntu,NDC-classes 和contact-high-school 数据集上表现出了较好的预测性能,这说明网络中节点之间的链接强度也可以精准地捕获网络结构信息.但是在一般情况下,单个特征指标仅仅在特定的网络中起到作用,并不能完全捕获整个网络结构的特性.而且这些特征无法有效表示高阶结构的特征,因此在大多数的数据集上表现不出较为优异的结果.

为了进一步分析本文提出的算法在部分数据集上表现较差的原因,我们从数据集本身进行分析,通过分析每个网络的聚集分布发现,一些预测结果较好的数据集的网络聚集程度较低,例如coauth-MAG-History,coauth-MAG-Geology 和NDC-substances 数据集.同时,一些预测结果较差的数据集的网络聚集程度较高,例如NDCclasses 和DAWN 数据集.这表明:如果节点间的聚集程度太高,整个网络趋向于完全图,则网络结构的聚集系数仅有较弱的参考价值.但是也存在例外,例如contact-primary-school 数据集聚集程度较高,但是实验结果也表现出了较好的性能.通过对该数据集分析,我们发现该数据集有较长的时间跨度,从而产生了丰富多样的结构.本文提出的时序特征主要通过将数据集进行切片划分从而捕获网络结构演变的关系,因此较长的时间跨度可以使得数据切分更加充分,进而促进划分后的网络结构演变特征充分发挥了作用.因此,数据集自身存在的特性也会直接导致本文提出的模型在部分的数据集上没有表现出较好的预测性能,这也是我们今后需要继续关注的问题.

虽然本文提出的算法无论与经典的链接预测算法比较还是与最新的基于机器学习的链接预测算法比较,性能上都表现的不错,但是这并不能说明本文提出的算法性能已经非常完美,因为高阶链接预测任务还具有挑战性.但是我们的目标是确定高阶链接预测中一些重要结构特征,而不是精确地进行预测.因此,我们将探索网络中更多潜在的可表示性特征作为未来的工作进行继续研究.

5 总结与展望

本文重点分析了链接预测的特点以及目前面临的难点问题,分析了网络中高阶结构的基本结构和特性,说明了在动态网络中进行链接预测的目的和意义.首先,从网络结构方面进行分析,提出了Motif 聚集系数,用于衡量高阶结构的聚集程度;其次,从时序维度分析,提出了可表示网络演变规律的节点间的链接频率和链接趋势等特征;最后,得益于神经网络对数据的建模能力,本文将高阶链接预测问题转换为二分类问题,从而采用多层感知器网络完成预测任务.为了进一步探索网络中更多潜在的可表示性特征,本文未来工作将会重点分析网络中的其他高阶结构特征,例如高阶结构中的结构中心性和结构相似性等特性,从而进一步挖掘网络中潜在的信息.