变位系数与螺旋角对斜齿轮动态啮合特性的影响
2021-05-22吕瑞杰韩炬杨再远
吕瑞杰,韩炬,杨再远
(1.滦州吉宏包装有限公司,河北 唐山063700;2.华北理工大学 机械工程学院,河北 唐山063210)
0 引言
齿轮传动的动态啮合性能对传动系统的振动、噪声、传递效率及传动平稳性等有重要影响,因此,对其深入研究是提高传动系统性能的关键。齿轮传动的动态啮合性能有多种影响因素,如材料性能、齿廓修形、变位、制造误差、装配误差等,国内外学者对此做了大量研究工作。
王志钦等[1]通过数值仿真研究了齿轮变位对啮合刚度的影响,陈安华等[2]研究了时变啮合刚度、啮合阻尼、支承刚度及支承阻尼对齿轮动态传递误差的影响,研究中没有考虑变位因素;Z. H. Zachary[3]开发了圆柱齿轮动态传递误差的测试系统;Hu Yumei等[4]应用有限元法分析了变位系数及螺旋角对斜齿轮瞬态啮合性能的影响;罗登峰等[5]探讨了变位系数和螺旋角对齿轮强度的影响,得出了要使最大滑动率相等,尽量采用高变位系数,并指出适当的负变位与大螺旋角也有利于提高斜齿轮副的承载性能;张义民等[6]应用有限元法对直齿轮传动的啮合特性进行了分析,研究了不同变位系数下的啮合频率及动态传递误差;吴勇军等[7-9]提出了接触有限元法并对齿轮-转子系统的连续啮合动态特性进行了分析;贲道春等[10]通过实践经验总结了管磨机齿轮变位系数分配的优化设计方法,提出了小变位、小滑动率差和小螺旋角的设计理念,降低了成本并提高了性能;刘学良等[11]基于有限元方法分析了变位系数对齿轮固有频率的影响。目前对齿轮动态特性的研究以有限元法为主,然而对于由多体组成的齿轮啮合系统的动态特性的分析,应用多体动力学法进行分析更为适合,过去由于多体动力学分析多假设物体为刚性体,因此其分析结果与实际出入较大,随着多体动力学平台的发展,其对柔性体、刚柔耦合体的分析研究结果的可靠性大大提高。
为适应复杂的工况要求,变位齿轮在传动系统中的应用日益广泛,变位系数的确定直接影响到齿轮副的装配尺寸、啮合特性及传动特性,因此在齿轮传动系统的设计过程中,变位系数的确定非常关键,本文将应用多体动力学方法,计及变位系数对斜齿轮啮合副的动态特性进行研究。
1 斜齿轮啮合副动力学模型

图1 齿轮副动力学模型
齿轮啮合过程中由于同时啮合的轮齿对数周期性变化,因此,齿轮的啮合刚度也具有时变性与周期性,且不同啮合轮齿的啮合刚度不同,目前齿轮动态特性研究大多采用A. Kahraman等[12]提出的动力学模型,该模型中的啮合刚度被认为固定不变,显然不符合实际情况。本文提出的齿轮啮合副的动力学模型如图1所示,本模型中将齿轮副看作柔性体,各啮合轮齿的啮合刚度分别为k1t、k2t…knt。
柔性多体系统与刚性多体系统类同,当系统中的柔性体变形与时间无关时,可退化为刚体系统,当系统中部件之间不存在大范围运动时,则退化为结构动力学问题,本文提出的齿轮副动力学模型中,主动轮与从动轮均为柔性体,将柔性体离散后,应用虚位移原理,可列出系统的运动微分方程:t
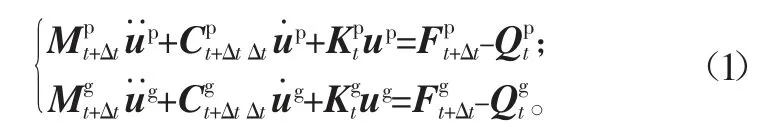
化简可得
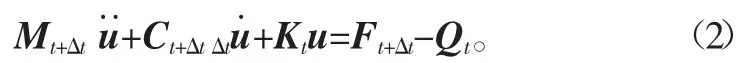
当考虑摩擦时,

式中:a为惩罚因子;N为单元节点插值函数;μ为滑动摩擦因数;s为位移增量;sT为切向分量;s1、s2分别为切向分量的两个方向上的量;gN为接触点之间的法向距离;eN为接触点法向单位矢量;e1、e2分别为两个切向的单位矢量。
2 斜齿轮传动分析模型
本文应用Creo Parametric构建了斜齿轮传动的全参模型,其基本参数如表1所示,齿轮副中的主、从动齿轮的材料属性一致,密度为7.83×10-6kg/m3,弹性模量为219 GPa,泊松比为0.3,模型计及摩擦与变位,不考虑齿轮修形。
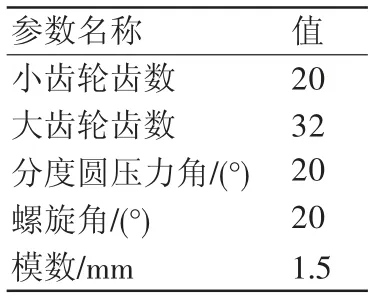
表1 斜齿轮传动基本参数
为更好地对齿轮传动过程中的轮齿接触力等进行研究,对分析模型进行柔性处理,在ADAMS中对主动轮与从动轮之间进行接触设置并添加运动副,本模型只考虑主动轮与从动轮,忽略支承轴、轴承及支架的弹性,仿真分析模型如图2所示。

图2 斜齿轮传动模型
3 仿真结果分析
为研究变位系数对齿轮啮合特性及传动特性的影响,采用的各组变位齿轮传动模型的变位系数如表2所示,保持主动轮不变位,从动轮变位,研究模型包括G1~G11共11组,分析求解器采用HHT-I3,静摩擦因数设置为1.1×10-2,动摩擦因数设置为1.0×10-2,设置各模型仿真时间为0.5 s。
3.1 系统传动误差分析
齿轮传动误差的产生原因很多[13],负载是关键影响因素之一,首先研究负载对传动误差的影响。表3所示为G1模型不同的负载情况。
图3为G1模型在不同负载下的输入输出角速度曲线,表4为运转平稳后各不同负载下的输出角速度均值及误差。
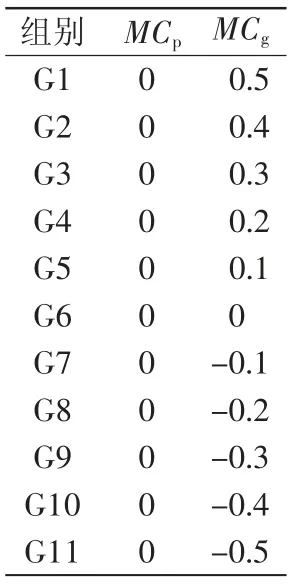
表2 不同模型变位系数设置

表3 G1模型负载设置
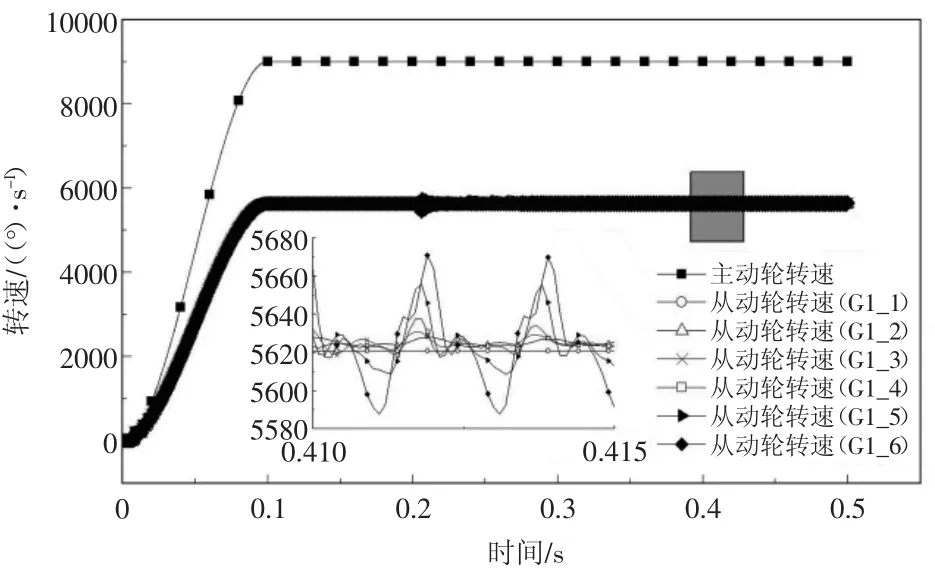
图3 传动机构输入输出角速度曲线

表4 不同负载下G1模型的从动轮转速
从图3可看出,当传动平稳后,从动轮转速呈周期性波动,且随负载增大,波动幅度增加,当空载时,转速的波动很小,其从动轮转速几乎为一直线,从表4的数据来看,当系统加载后,随负载增大,从动轮转速误差增加,但加载时的转速误差均小于空载。表明适当的加载对提高传动精度有益,但加载后会引起转速的波动,从而使齿轮副啮合过程中产生振动与噪声。
图4为G1_5模型的从动轮受力曲线,从局部放大图中可以看出,轮齿受力呈周期性波动,意味着齿轮副的啮合刚度具有时变性与周期性,齿轮副啮合刚度的变化与传动过程中齿轮副的啮合齿数的变化有关。图5所示为G1_5模型在负载情况下的轮齿受力图,图6标示了轮齿的标号,从图5中可以看出,在一个周期内,受力轮齿对数的变化规律为1→2→3→2→1,啮合齿数的变化是啮合刚度时变性的关键原因。
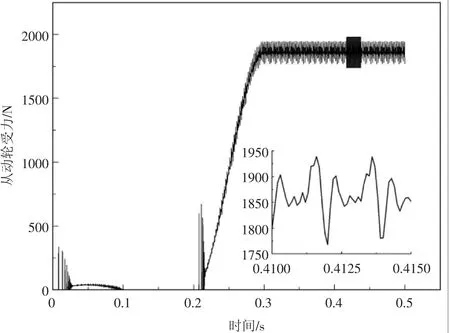
图4 从动轮受力曲线图
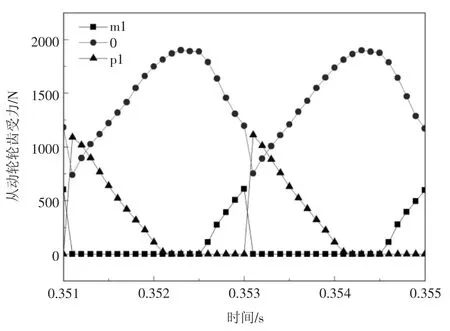
图5 齿轮轮齿受力曲线图
图7所示为G1模型在不同负载情况下的动态传动误差曲线。从图中可明显看出,传递误差曲线具有周期性,运转平稳后,空载时的波动最大,但频率最小,这与图3中空载时从动轮的转速曲线基本平直吻合,负载情况下的传动误差波动频率基本一致,且从图8的G1_5模型的传动误差的幅频曲线中可以看到,虽然曲线具有明显的低频特征,但也包含大量的高频成分。

图6 齿轮轮齿标号图
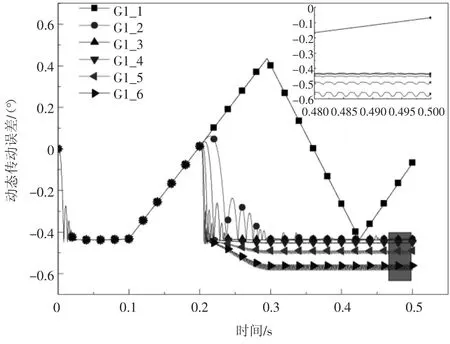
图7 G1模型动态传动误差曲线

图8 G1模型负载时传动误差幅频曲线
图7中空载与负载工况下的传动误差差别较大,空载情况下,传动误差波动较大,且波动幅值在正负之间变换,而负载情况下,动态传动误差波动较小,且传动误差为正,从放大图中可以看出传动误差曲线具有多组正弦曲线叠加后的形态。传动误差的波动与系统啮合刚度的变化是对应的,由于运转平稳后,系统负载恒定,且没有考虑修形、制造及装配误差等因素的影响,因此,可以根据传动误差的波动情况,计算出系统的时变刚度。图8所示为G1_5模型的传动误差曲线经过傅立叶变换后得到的幅频曲线,从放大图中可看出,虽然曲线具有明显的低频特征,但也包含大量的高频成分,反观空载时的传动误差幅频曲线,基本不含高频信号。
3.2 变位系数对动态啮合性能的影响
为研究变位系数对斜齿轮啮合副动态性能的影响,对G1~G11共11组模型进行仿真,各模型的仿真时间均设为9000d*step (time,0,0,0.1,1),负载均设置为4.2e4*step(time,0.2,0,0.3,1)。图9~图11分别为变位系数对传动误差、轮齿最大受力及最大相对滑动速度的影响。
由图9可知,变位系数对传动误差影响明显,对于研究所涉及的模型,当变位系数在-0.3~0.3范围内变化时,变位系数的增加与传动误差成反比,变位系数越大,误差均值与误差波动越小,尤其需要注意的是,在本模型中适当地采用变位设计有利于传动误差的降低,且当从动轮正变位时,传动误差随变位系数先减小、后增大,当从动轮负变位时,传动误差随变位系数先增大、后减小。由图9数据可知,在11 组模型中,当从动轮变位系数为-0.5时,其传动误差均值及其波动最小。

图9 变位系数对传动误差的影响
图10为不同变位系数下轮齿最大受力均值走势图。由图10可以看出,当变位系数从-0.5变化到-0.4时,轮齿受力增大幅度很小,但从-0.4变位到-0.3时,轮齿最大受力急剧增大,增长了近10倍,然后当变位系数从-0.3变化到0.3时,轮齿最大受力逐渐减小,基本呈线性变化。图9与图10形成了相互印证,当传动误差均值及传动误差波动大时,轮齿最大受力也相应较大。结合图9与图10可以看出:当变位系数分别为0.3、0.4、0.5时,其轮齿最大受力基本一致,但传动误差有大幅增加;当变位系数为-0.4与-0.5 时,其轮齿最大受力基本一致,但传动误差有大幅差距。

图10 变位系数对轮齿最大受力的影响
图11为不同变位系数下轮齿最大相对滑动速度走势图。最大滑动速度是轮齿齿面磨损的重要指标,从图11中可看出,最大滑动速度随变位系数的增大而减小,尤其当变位系数为0.3时出现突变,滑动速度急剧下降。
综合前述变位系数对传动误差、轮齿受力及最大滑动速度的分析,可以看出,在本文涉及的斜齿轮副中,对从动轮进行0.3的变位会得到更好的动态特性。

图11 变位系数对最大滑动速度的影响
3.3 螺旋角对齿轮副动态啮合性能的影响
为研究螺旋角对斜齿轮啮合传动动态性能的影响,选择G3模型进行分析,此时主动轮不变位,从动轮变位系数为0.3,螺旋角的选择如表5所示。

表5 螺旋角参数设置
图12为螺旋角对动态传动误差及其波动范围的影响走势图,一般斜齿轮的螺旋角的选取角度为[8°,20°],随着螺旋角的增加,传动误差及其波动范围先减小后增大。从图中可以看出当螺旋角为14°时,传动误差最小。

图12 螺旋角对传动误差的影响
图13 为螺旋角对轮齿最大受力的影响曲线。由图12与图13可知,螺旋角对轮齿最大受力与传动误差的影响走势相关,当螺旋角由8°变为10°时轮齿受力增大,传动误差也随之增大,当螺旋角由10°变为14°时,轮齿最大受力急剧下降,相应的传动误差也大幅降低,但当螺旋角从14°增大到20°时,其轮齿最大受力的虽依次增加,但幅度很小,然而此时的传动误差却大幅增加。因此,应该慎重选择螺旋角,在保证轮齿受力较小的情况下,应尽量使得传动误差较小。
图14为螺旋角对最大滑动速度的影响曲线,从图中可看出最大滑动速度与螺旋角基本成反比关系,且变化比较平缓,图中显示,只有当螺旋角从18°变为20°时,其变化才相对剧烈。该曲线与图12、图13体现出来的明显的非线性特点区别较大,表明螺旋角的选择相对比较复杂,不像变位系数那样明确。

图13 螺旋角对轮齿最大受力的影响
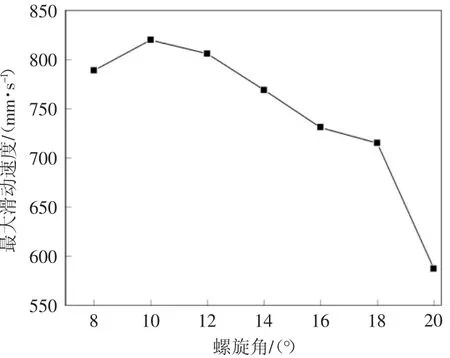
图14 螺旋角对最大滑动速度的影响
综上分析可知,当螺旋 角 为14°时,斜齿轮副的动态特性较好。
4 结论
本文基于多体动力学方法对斜齿轮啮合副的动态特性进行了精确分析,与有限元法进行的静态分析与瞬态动力学分析相比,结果更具可靠性,通过分析得出以下结论:1)齿轮副系统的传动误差具有明显的周期性,当空载时,传动误差变化频率低,加载后传动误差变化频率大幅提升,适当增加负载对提高齿轮传动精度有利。2)当从动轮负变位时,斜齿轮啮合副动态特性随着变位系数的减小,先有所下降再有所提升;当从动轮正变位时,动态特性随变位系数的增加先有所提升后有所下降。3)螺旋角对系统动态特性的影响不像变位系数那样明确,螺旋角对传动误差、轮齿最大受力的影响的相关性一致,具有明显的非线性特点,随着螺旋角的增大,传动误差与轮齿最大受力先提升后下降;但螺旋角对最大滑动速度的影响具有明显的线性特征,最大滑动速度随螺旋角增大而减小。
本文的目的主要在于探讨变位系数及螺旋角对传动系统动态特性的影响,为简化模型,没有考虑轴、轴承及支架的弹性,在以后的研究中将全面考虑,以构建更为精确的分析模型。
