电力运行类数字孪生系统稳态逆向建模研究

常 春，吉炫颖，朴永鑫，王继华

（1.国网吉林省电力有限公司通化供电公司，吉林 通化 134001；2.北京四方继保自动化股份有限公司，北京 100085）

0 引言

在工业互联网［1］的大背景下，高度自动化、数字化和网络化的发展趋势在工业领域已备受关注［2］。针对高度数字化的发展方向，各行各业结合通用类仿真系统或者本领域内的专用仿真系统展开了全面深入的研究探索，如车间制造、飞机装备等领域［3-5］。电力物联网［6］也契合了此发展方向，基于传统电力运行类仿真模型衍生出的在线仿真、数字孪生、平行系统、数字双胞胎等领域的研究成为热点课题［7］。

针对电力行业的数学模型，有学者采用数据分析技术进行探讨［8］，也有学者基于机理模型理论进行分析［9］。本文面向电力运行类领域，采用专用机理建模与数据分析相结合的技术，提出了一种搭建数字孪生系统数学模型的方案，并讨论了针对其稳态状况逆向建模的技术路径，为孪生系统进一步研究和应用打下理论基础。

1 电力运行类数字孪生系统

1.1 数字孪生系统结构

数字孪生系统结构如图1所示，通常包括实体层、数据层、模型层和应用层。

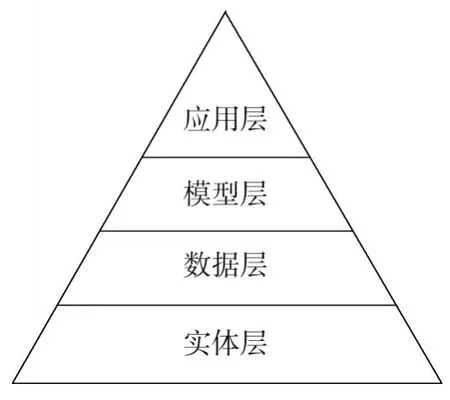
图1 数字孪生系统结构图

实体层是指实际工业生产过程中独立运行的实体，涉及电力系统的一次设备、二次设备，以及其他控制系统等。

数据层是实体层和模型层的桥梁。通过传感器、通信协议、信号传输等手段将实体层的必要信号进行采集、汇总和处理，并将其传递给模型层使用。

模型层是物理实体的数字化模型。该部分是基于机理模型驱动与大数据分析驱动相结合的数字模型，该模型保持与实体层数据实时同步。

应用层是基于模型层中模型运行数据的高级应用。该层为实体层的生产运行提供实时全方位、全生命周期监控等功能应用。

1.2 电力运行类数字孪生系统特征

电力运行类数字孪生系统具有本行业独有的一些特征：

1）安全性。数字孪生系统需接入电力生产系统采集数据，在分区操作及数据传输方向等方面要格外重视。

2）模型连续性。电力运行过程的数学模型涉及到能量变化、能量传递等热力、电力类连续函数建模。

3）实时性。为保证数字孪生系统及时准确反应电力生产实际情况，电力生产过程中的被控信息需要实时准确地传递给孪生系统。

4）多变性。变电站等运行实体通常具备不确定性，即使在重要参数一致的状态下，其仿真模型内部的数据也会随着外界运行状态而不同。

5）独立性。数字孪生系统可实时采集实体层数据，使实体层与模型层同步运行，也可以脱离实体层独立运行、超前计算。

6）自修正性。模型层需根据实体层传输来的数据周期性进行学习并自修正，使本身的模型特点与实体层尽可能保持一致。

7）采样信息不足。电力运行类的实体规模以及目前的控制策略导致了现场的信号采集不能覆盖所有实体设备，这为孪生系统的建模带来了难度。

8）超前性。电力运行类的数字孪生意义在于可以使系统模型超前运行，从而判断并预测出作用在实体系统上的激励信号可能得到的响应。

1.3 研究步骤

一个完整的数字孪生系统建模流程：构建数据层，将实体层输入的数据整理为模型层可以使用的数据并将其输出；构建物理实体对应的数字模型，并且通过机理运行、大数据分析等方式不断修正模型；将模型运行的数据结果导入应用层，经高级分析得出结论。

结合电力系统模型连续性的特点，数字模型可分为稳态同步及动态同步两部分。本文重点研究稳态同步部分逆向建模的方案。

模型建模结构如图2所示。数据层的输入通信模块可将实体层的必要信息收集汇总。为保证安全性，该模块设计了工业单向隔离装置及防火墙，确保其不会干扰安全生产的物理实体层；为保证实时性，该模块依据香农定理、模型运行精度等信息确定数据采样频率的最低值，确保模型可以精准辨识。

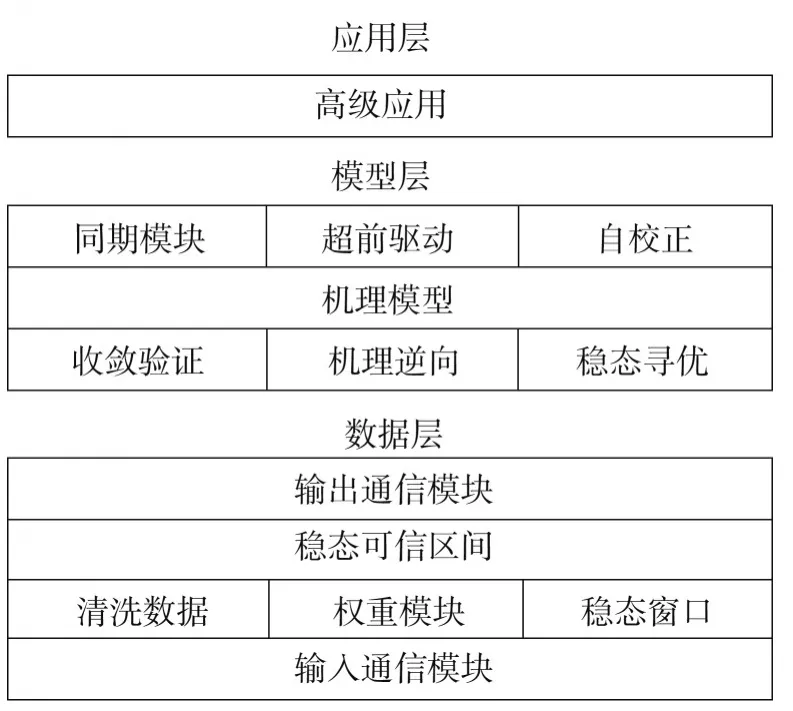
图2 模型建模结构图

考虑到数据的多变性，设计清洗数据模块消除异常点、坏点等导致的毛刺现象以及扰动、丢包导致的偏差现象，获取逼近真实现场的可用数据。针对获取到的数据对系统的重要程度不同，设计权重模块，标明各个数据在模型辨识过程中的容错参数；针对稳态识别的建模目的，设计稳态窗口模块用来从采样数据中寻找出可用的稳态窗口。通过上述模块配合，最终得到稳态可信数据区间。该数据通过输出通信模块传递给模型层。

鉴于系统的独立性，模型层基于机理模型开发，确保该孪生系统可以对外部激励作出正确的响应。因为采样信息不足，针对其中一部分可反向计算的数据，设计机理逆向模块；其他数据，设计稳态寻优模块，同时根据寻优评价标准建立收敛验证模块，进而得到所有的与物理实体结果一致的稳态模型数据。

针对基于校正后的模型运行结果与物理实体间的误差必然存在的问题，设计同期模块，使二者可以保持瞬间及阶段性同步；针对超前性的要求，设计超前驱动模块实现孪生模型超前运行；针对自修正的要求，设计阶段性自校正模块，从而实现模型与物理实体的同步运行。

应用层对模型运行结果进行各种高级应用计算，通常涉及故障诊断、操作验证等。

2 稳态模型逆向建模步骤及数学模型

2.1 数据层数学模型

假设本次自实体层采样的频次为n，则共得到n组不同的数据集合，记作Ω=｛X1，…Xj…，Xn｝。其中Ω为初始采样数据矩阵，Xj为第j次采样的数据集合。

假设实体层每周期采样提供的数据规模为m，那么Xj=｛x1，j，…，xi，j…，xm，j｝，其中xi，j表示第i个变量在第j次采样时的数值。由此，Ω可表示为：

χi={xi，1，…xi，j…xi，n}，表示第i个变量的n次采样数据集合，Ω又可表示为Ω={χ1，…，χi，…，χm}。

在清洗数据模块中，采用合适的滤波算法进行数据处理，此处采用加权递推平均滤波法对每个变量的n次采样数据进行处理，记为χ′i=Filter(χi)，其中χ′i表示将第i个变量的n次采样数据集合χi滤波后得到的集合。

同理，依次作用于所有变量得到整体数据清洗后的结果，记为：

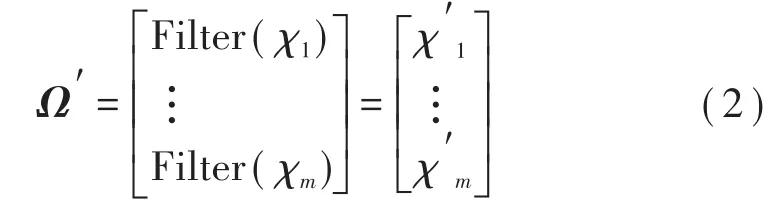
权重模块中，针对每一个变量集合χi引入其上限Ui，下限Li，同时引入容错参数αi。其中上下限信息均由系统导出，αi∈[0，100%]。容错参数的数值和重要性成反比，即越重要的数据的容错幅度越小。

稳态窗口模块需要在n次采样数据中寻找一个稳定窗口，使得该时间段内的m个变量采样值均围绕在均值附近的容错范围内。得到的稳态窗口为：

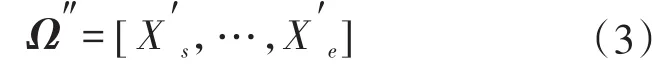
式中：X′s和X′e分别表示窗口开始、结束时刻对应的数据集。

矩阵Ω″的第i行变量χ″i表示稳态窗口数据集中第i个变量的数据集合，该集合中的所有数值满足以下条件：

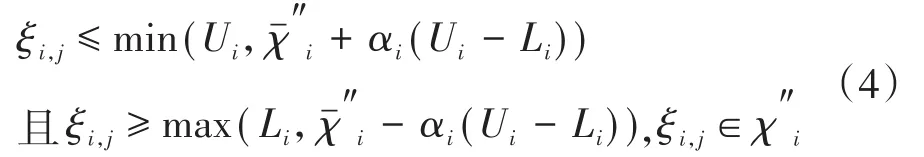
最终得到如式（5）所示的稳态可信区间，通过输出通信模块传递给模型层。

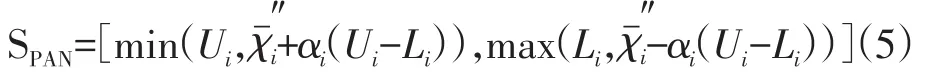
2.2 模型层数学模型

模型层中的数学模型以机理建模为主，模型记作Ψk+1=F(Ψk)，其中F表示模型函数，Ψ表示模型中所有的变量。

模型层的收敛验证模块可检测仿真模型F在给定的模型数据Ψ下是否稳定。数学模型描述为：

对于任意ε＞0，存在一个k，使得Ψk+1-F(Ψk)＜ε，则称为模型F在状态Ψ下收敛，记为Ψk+1→F(Ψk)，k→∞。

在机理逆向模块中，将该模型中所有的变量分为3类，记为Ψ={X，Y，Z}。

X表示数值区间中可由数据层获取的变量集合，即表示实体层关注的变量，X∈SPAN。

Y表示在已知数据基础上，经过机理反向逆运算推导出的具有确定数值区间的变量集合。利用已知数据X及经X推导出来的Y，最终得到Y的取值区间，。

Z表示受到X和Y的约束，但数值区间不确定的变量集合。

通过多组逆向函数，可以得到X、Y的区间确定值。此时需要引入最优化求解或者概率估计等方法来确定Z的数值。

在模型运行的历史数据库中，对稳态工况下的数据进行索引匹配，寻找当X、Y满足现有区间要求时Z的取值范围。倘若匹配失败，则暂时将Z的取值范围定为上下限之间，即。

得出所有变量的取值区间，在此基础上求解最优化方程：

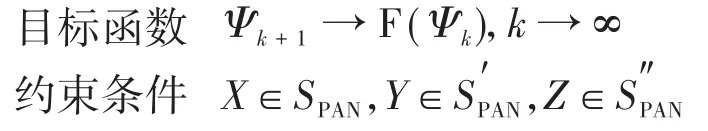
采用常规最优化数值求解算法，最终得出变量的确定数值。

3 应用层场景

收敛完毕的稳态数学模型需要和实体层数据并轨同步运行，在此基础上设计周期自修正、超前运算、动态跟随等高级应用。应用层状态转移如图3所示，图中展示了各种状态的切换过程。

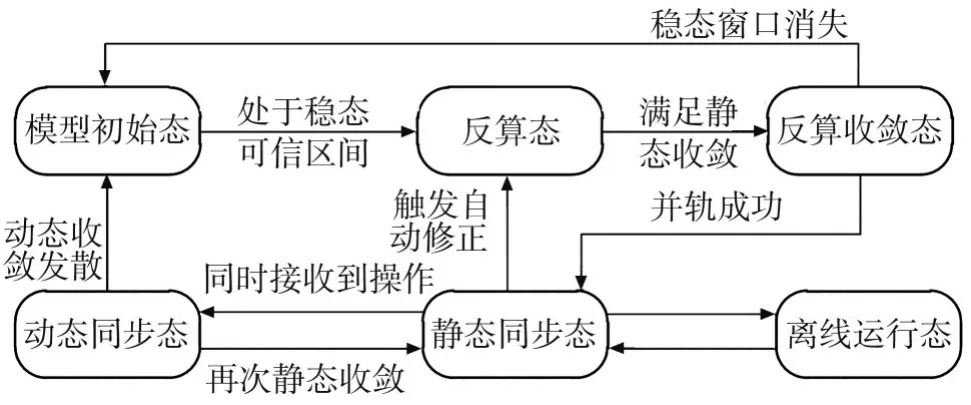
图3 应用层状态转移图

该系统启动后，处于模型初始状态。当监测到实体数据的信号处于稳态可信区间时，系统进入逆向运算的反算态。经过复杂的反算过程，满足静态收敛条件时，系统进入反算收敛态。倘若此时稳态窗口消失，则转回模型初始态，否则进行并轨操作，成功后进入静态同步态。

系统进入高级应用场景时，为了保证孪生模型与实体系统实时一致，系统会由时间/事件触发器将模型切入模型反算态进行自动修正操作，从而时刻保持数学模型与真实系统完全同步。

系统可以随时进入离线运行态，进行超前运行操作。将预实施于真实系统的激励应用到数学模型上，从而提前得到趋势响应。试验结束后，再次进入静态同步态。

当数学模型与真实系统同时接受到运行操作指令时，系统进入动态同步态。倘若再次回归至静态收敛模式则进入静态同步态，否则返回模型初始态。

4 结语

利用数学模型，在稳态状况下系统经过机理逆向运算及大数据分析实现模型同步。通过同期模块实现数字系统与物理实体接轨运行；通过超前驱动模块实现模型层对事故的提前预判；通过自校正模块，来避免模型长期独立运行累计的计算误差，进而指导实际生产运行。稳态逆向模型同步功能是数字孪生技术发展中的必经阶段，在此基础上可开展动态模型同步功能，从而完善孪生系统同步效果。

相比传统仿真，数字孪生系统的引入使电力运行类工作有了真正意义的同步数字系统。该系统的精细度与准确度直接决定了数字孪生系统在物理实体运行工作中的指导意义。