天然气水合物赋存地层的地震波场模拟及对比
2021-05-21刘洋廷张晓波郑彦鹏
范 金,刘洋廷,张晓波,刘 凯,郑彦鹏*
(1.自然资源部 第一海洋研究所,山东 青岛266061;2.青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室,山东 青岛266237;3.国家深海基地管理中心,山东 青岛266237)
在中低纬度地区,天然气水合物是一种由充足的气源、水源在高压(一般大于10 MPa)和低温(一般小于10℃)条件下络合而成的笼形结晶化合物[1-2]。因水合物的气源成分以CH4为主,另有少量CO2和H2S等气态物质,它又被称为“甲烷水合物”。天然气水合物主要分布在陆地的永久冻土带和大陆边缘水深超过300 m的陆坡带[3-4],在我国典型的矿藏区分别是祁连山冻土区和南海北部陆坡区。国际地质调查部门将其认定为地球上尚未大规模开发的可替代性清洁能源,对全球气温变化和碳循环过程有至关重要的作用[5]。
由于地质和地球物理条件的不同,天然气水合物以不同的状态赋存在地层中。在研究不同区域的水合物时,根据水合物与骨架颗粒的接触关系、沉积物的粒度等要素,赋存状态有多种划分方法[6-9]。胡高伟等[10]发现沉积孔隙中的水合物呈混合分布,在不同的形成阶段会以某种分布状态为主导。近年来,学者发现标志天然气水合物存在似海底反射(Bottom Simulating Reflections,BSR)、振幅空白、速度异常和极性反转等地震异常信息[11]。高精度地震勘探技术已成为圈定天然气水合物成矿区的主导技术,它的基本任务是通过人工地震激发的各种地震波数据反映含水合物沉积层的地质信息,实现对水合物矿藏的精准定位。地震波场的正演模拟是地震勘探的基础。通过对不同正演模拟方法的改进,Dablain[12]、何兵寿等[13]、Liu和Sen[14]的研究成果不仅保证了计算精度,而且降低了计算成本;基于Biot-Gassmann理论,Lee[15]提出一种可预测未固结的含水合物沉积层物性特征的方法;Cordon等[16]利用正演模拟方法研究水合物储层中的衰减特征,发现衰减导致的振幅减小可能会影响水合物体积预测的程度。随着探测方法和技术的不断提高,天然气水合物在沉积层中的赋存状态不断被重新认识;然而,前人并没有开展不同正演模拟方法识别不同赋存状态水合物差异性的研究。
通过研究天然气水合物在地层中的赋存状态,本文总结了水合物6种不同的赋存状态:颗粒间胶结型、颗粒包裹型、颗粒支撑型、孔隙充填型、基质与填充物共存型和结核/裂缝型,并讨论了其相互转化的关系,概述了相应物性参数的计算方法;介绍模拟含水合物沉积层地震波场的声波模型、弹性波模型和双相介质模型,根据水合物6种赋存状态设定适合的孔隙度、饱和度等,基于物性参数计算方法求出地层的弹性参数并分别应用到3种正演模型中;改变沉积层的厚度、子波主频信息,借助波场快照与地震记录直观地反映含水合物沉积层的地震特征,对不同赋存状态水合物地震响应的差异性进行对比和分析,为识别水合物的勘探研究以及指导地震波反演、成像等提供依据。
1 水合物的赋存状态概述
天然气水合物的微观分布主要指水合物和沉积物颗粒在地层中的接触关系[17]。微观分布又称为赋存状态。天然气水合物在地层中的6种赋存状态及其关系转化见图1。状态1和状态2属于胶结状态,将岩石颗粒视为随机填充的球体,水合物发生在接触点(状态1)或在颗粒周围生长(状态2)。当仅存少量的水合物时,预测的弹性性能大幅增加,随水合物浓度的逐步增加而保持相对接近[7]。在状态2中,水合物和沉积物胶结良好,这在降低孔隙度的同时,极大改变了沉积物的刚度[18-20]。水合物在状态3中起着颗粒支撑作用,孔隙一般被水和/或游离气等非黏滞性流体充填,沉积物的剪切性质不受影响;水合物在固体颗粒边缘沉积并向孔隙空间内部生长,影响岩石的刚度和热传导性质。值得注意的是,随着饱和度的逐步增加(过程一),水合物可能会由状态1转变成状态2,甚至是状态3。水合物在状态4中起填充孔隙的作用,充填物包括水合物、水或游离气,每种组分的弹性性质各有不同,所以诱发的孔隙压力也不尽相同;当水合物的饱和度较高时,水合物颗粒与相邻的固体矿物颗粒相桥连,成为固体基质的一部分,增强固体骨架的力学稳定性,状态4就可能变为状态3,导致地层刚度变弱[21]。状态5是分别将骨架颗粒和水合物作为基质和填充物处理,作为夹杂物嵌入均匀介质中。状态1~状态5都被认为天然气水合物在沉积物中均匀分布,而水合物取芯的证据表明,水合物通常作为浅层泥质沉积物中的结核和裂缝填充物存在,该几何形态在状态6中示出[7]。产出于裂缝内的水合物迫使地层岩石张开形成裂缝并充填其中,一般呈网状、结核状或脉状,肉眼可观测到呈乳白色晶体状。含水合物层不仅有较大的裂缝倾角,更受区域构造主应力控制[22]。水合物处于状态3且在局部的饱和度逐渐升高时(过程二),就可能转变成状态6。如图1中蓝色箭头所示,在实际的形成过程中,天然气水合物可能首先是胶结沉积物颗粒(状态1),中期以接触沉积物颗粒或悬浮在孔隙中(状态3或状态4)为主,后期又以胶结形式(状态2)为主,即多种赋存状态共存。学者认为游离气的存在和水合物体量增大可能是造成这种变化产生的原因[10,23]。
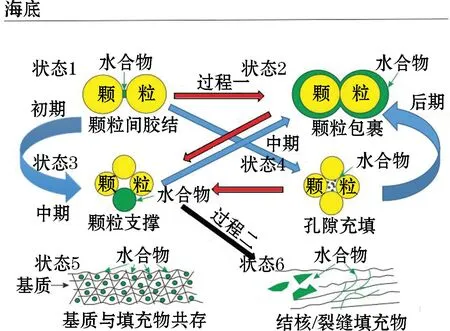
图1 天然气水合物在海底的6种赋存状态[7,10,21-23]Fig.1 The six main occurrences of natural gas hydrate below the sea floor[7,10,21-23]
不同类型水合物的存在对沉积层的声学特性有直接的影响,会产生不同的地震波场特征。含不同赋存状态水合物沉积层的物性参数计算流程见图2。当沉积层中不含水合物时,按照图中主干部分(黑色边框)的计算流程,代入相关的参数值,求出地层整体的弹性模量、密度、速度;当沉积层中储存水合物时,根据不同的赋存状态,选择图中分支部分(彩色边框)相应的计算流程,求出含不同赋存状态水合物地层的弹性模量、密度、速度。然后,根据不同的正演模型(图2中黑色实心箭头),确定相应的参数。因篇幅所限,本文对计算公式不做具体介绍,详见文献[6,22,24-25]。

图2 含水合物沉积层的物性参数计算流程Fig.2 Flow chart for calculating physical parameters of hydrate-bearing sedimentary layer
2 正演模拟的理论模型
地震波传播理论是各类地震学科的基础,核心内容之一就是地震波传播和介质模型[26]。弹性波动方程是地震波传播的动力学核心,解释了地震波在复杂地层中的传播机理。不同的模型中介质的速度、相态、密度等参数的计算方法各有不同,主要通过孔隙度和饱和度来界定,进而影响地震波的传播。本文主要使用二维各向同性的声波模型、弹性波模型和双相介质(即孔隙流体介质)模型,其波动方程详见文献[27-29]。在地震波场的模拟方法中,有限差分法因实现简单、计算效率高等优势被应用于多项研究。董良国等[30]将高阶差分法和交错网格相结合,这一方法目前在地震波场数值模拟研究中被广泛使用。除此之外,差分格式的相容性、收敛性、稳定性和边界条件等问题也已被前人研究[27-28,30-33]。
参考Ecker对海底沉积物的参数设定[20],本文模拟的沉积层中各矿相的物性参数值见表1,其中沉积骨架由5%的石英、35%的方解石和60%的黏土共同构成[34]。为对比3种正演模型的差异,设计了一种双层模型(图3),物性参数见表2;其中,上部是孔隙度为35%的饱水沉积层,下部是孔隙度为20%的饱水沉积层。计算模拟的波场空间为1 500 m×1 500 m,网格大小为5 m×5 m,时间步长为0.5 ms。采用交错网格有限差分法,精度为时间2阶、空间10阶。震源采用主频为25 Hz的雷克子波。

图3 双层模型Fig.3 Two-layer model

表1 沉积物中各矿相的物性参数Table 1 Physical property parameters of various mineral phases in sediments

表2 双层模型的物性参数表Table 2 Physical property parameters of two-layer model
图4 是0.25 s时刻地震波在3种模型中传播的网格化波场快照,展现了清晰的差异性:激发纯纵波在声波介质中波阻抗界面只存在透射和反射;当地震波到达弹性介质的波阻抗界面时,除了产生透射和反射,还会产生转换波;区别于弹性介质,震源在双相介质中会产生与快纵波相互伴生的慢纵波。慢纵波在实际地层传播过程中具有极大的衰减性,在波阻抗界面也会产生更多类型的地震波。观察波场快照还可知,基于等效弹性模量模型和Biot理论计算的双相介质参数,模拟的纵波走时与声波介质、弹性介质中纵波走时存在明显的差异,主要是由不同的拉梅系数计算方法导致的。

图4 0.25 s时刻地震波在3种模型中的网格化波场快照Fig.4 Meshed snapshots of seismic waves in the three models at time 0.25 s
3 波场模拟及对比分析
根据4个不同的层状模型(图5),设计了合理的地层孔隙度、不同赋存状态下水合物的饱和度以及游离气的饱和度,并依据图2的流程来计算相应层位的物性参数(表3)。采用与前文相同的波场空间、采样间隔和震源类型。在海水中激发纯纵波,炮点位于近海面处,检波器排列于炮点下方,61道接收,道间距为25 m。采用PML吸收边界,只考虑地震波在介质中的传播。对含不同赋存状态水合物的沉积层进行了大量的正演模拟分析,并挑选出几种含水合物沉积层的波场快照和地震记录,展开对比与分析。
层状模型1从上往下分别是海水层、饱水沉积层、含孔隙充填型水合物沉积层和饱水沉积层(图5a)。图6~图8给出了低频(子波主频采用25 Hz)条件下,在声波介质、弹性介质和双相介质分别模拟不含游离气的孔隙充填型水合物沉积层的典型波场快照、去除直达波的单炮地震记录和含水合物层底界振幅随偏移距变化的曲线。1)对比波场快照(图6)可知,地震波在声波介质中的反射波能量要明显强于弹性介质和双相介质,主要是因为纵波在弹性介质中向上部地层反射时,遇到了向下部地层透射的横波,产生能量耗散;在双相介质中,地震波不仅发生能量耗散,且孔隙流体的存在导致地震波将能量按孔隙度大小分配给了固、流相,反射振幅进一步减小。2)对比地震记录(图7)可知,当含水合物层下伏的沉积层中不含游离气时,声波介质和弹性介质模拟含水合物层底界只表现出与海底反射极性相同、与水合物层顶界反射能量相近的反射;双相介质模拟含水合物层顶界的反射微弱,但底界的负极性反射异常明显。3)从含水合物层底界振幅随偏移距变化的曲线(图8)可知,由于所提取曲线受到了其他波的干扰,造成个别位置产生局部跳动,但不影响整体的变化。随着偏移距的增大,声波介质模拟的反射振幅明显增大,弹性介质模拟的反射振幅整体上减小,而双相介质模拟的底界振幅是先增大后减小。

图5 正演模拟与对比所需的层状模型Fig.5 Forward simulation and layered model for the purpose of comparison
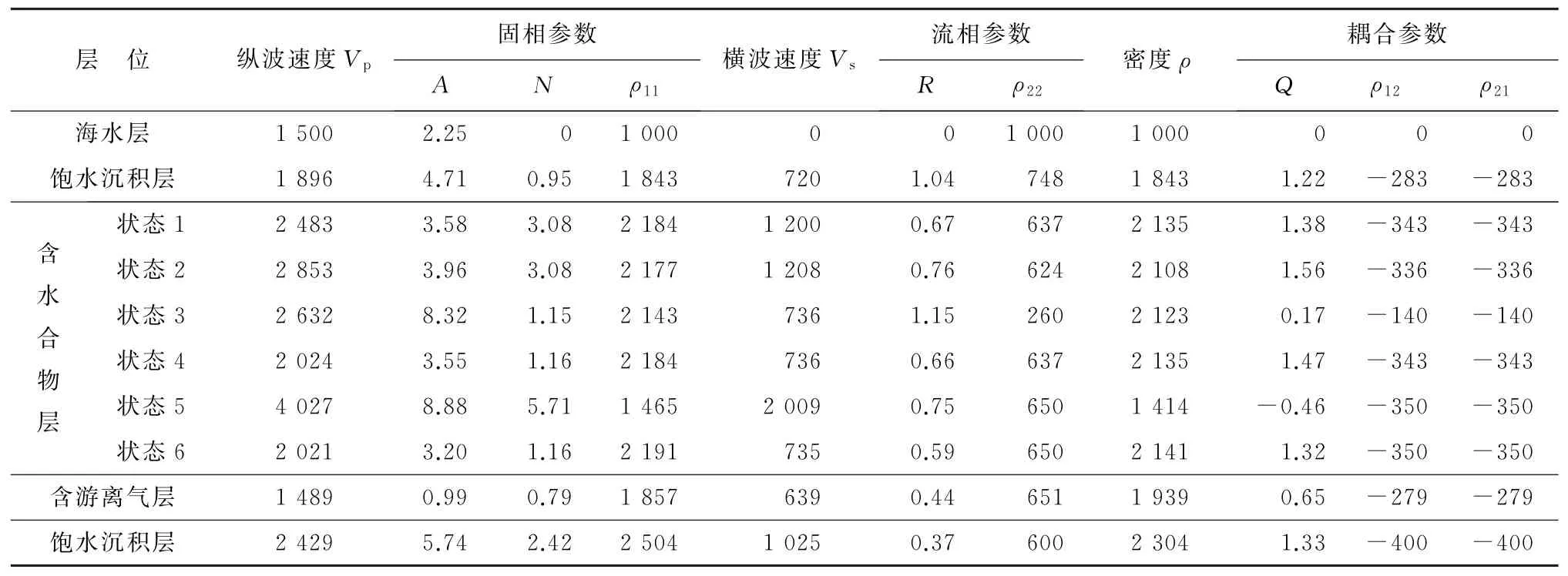
表3 基于等效弹性模量模型和Biot理论计算的层状模型物性参数Table 3 Physical property parameters of layered model calculated based on equivalent elastic modulus model and Biot theory
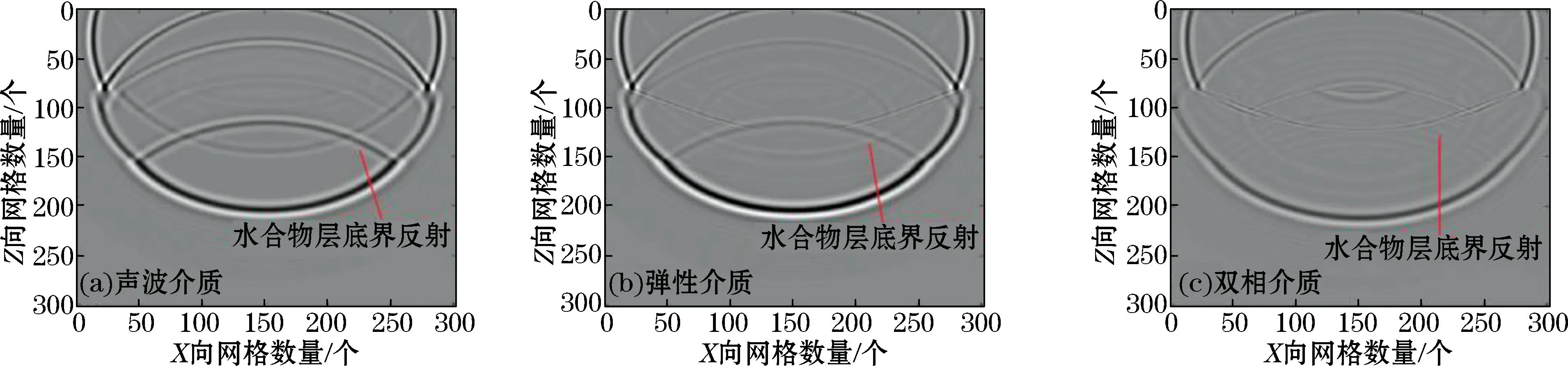
图6 模拟孔隙充填型水合物的网格化波场快照Fig.6 Snapshots of gridded wavefields that simulate pore-filling hydrates

图7 模拟孔隙充填型水合物的去除了直达波的单炮地震记录Fig.7 A single shot seismic record that simulates pore-filling hydrates with direct waves removed

图8 模拟含孔隙充填型水合物层底界振幅随偏移距变化的曲线Fig.8 The variation curve of the base amplitude of the simulated pore-filling hydrate layer with offset
层状模型2从上往下分别是海水层、饱水沉积层、含颗粒包裹型水合物沉积层、含游离气层和饱水沉积层(图5b)。低频(子波主频采用25 Hz)条件下,在3种介质分别模拟含游离气的颗粒包裹型水合物沉积层的正演结果。图9~图11分别展示了正演模拟得到的波场快照、单炮地震记录和含水合物层底界振幅随偏移距变化的关系。1)从波场快照(图9)可知,地震波在3种介质中反射的能量大小关系与图6相似,且含水合物高速层与含游离气低速层的界面反射与海底反射极性相反。2)对比地震记录(图10)可以看出,3种介质模拟水合物底界都有清晰的BSR响应[35],与波场快照的现象吻合;弹性介质和双相介质模拟含水合物层底界的振幅在红色边框处突然变小,而声波介质模拟不存在这一现象。究其原因,猜测是由于临界角的变化或者是极性相反的波形相叠加造成的。3)从振幅随偏移距变化的曲线(图11)可知,随着偏移距的增大,声波介质模拟水合物层底界的反射振幅整体上先保持稳定,后快速增大;弹性介质模拟水合物底界的振幅先缓慢减小,后产生震荡式变化;双相介质模拟水合物底界振幅整体上呈震荡式减小。与图6~图8相比,当含水合物层下伏沉积层中含游离气时,无论使用哪一种正演模型,水合物层底界的负极性反射都尤为明显。区别于图9~图11,将子波主频提高为40 Hz后,地震波形变窄。声波介质模拟水合物底界的反射振幅连续性较好,弹性介质和双相介质模拟水合物层底界的同相轴出现振幅突然减小的特征。相比于图9~图11,提高子波主频对3种正演模型识别含水合物沉积层的影响不大。

图9 模拟颗粒包裹型水合物的网格化波场快照Fig.9 Snapshots of gridded wavefields that simulate particle-encapsulated hydrates

图10 模拟颗粒包裹型水合物的去除了直达波的单炮地震记录Fig.10 A single shot seismic record that simulates particle-encapsulated hydrates with direct waves removed
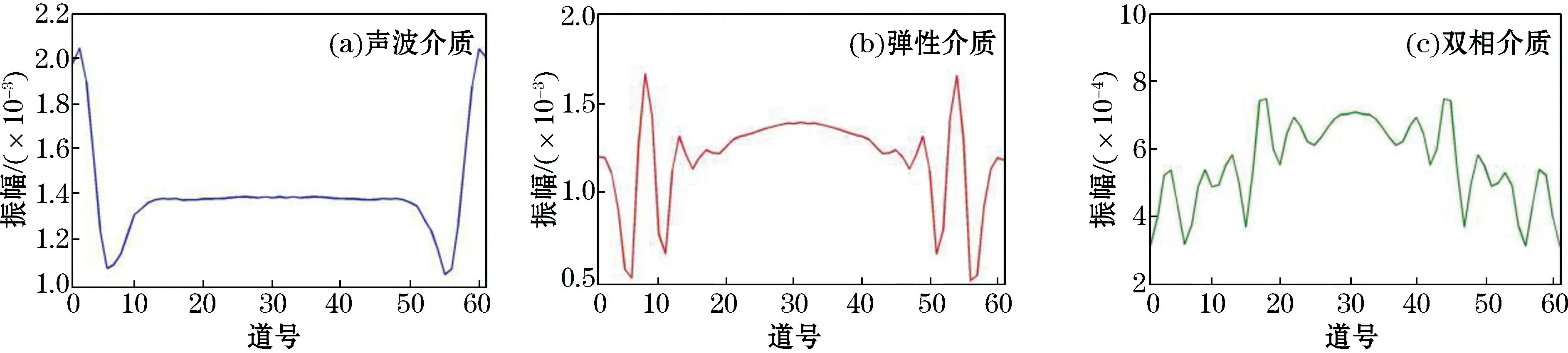
图11 模拟含颗粒包裹型水合物层底界振幅随偏移距变化的曲线Fig.11 The variation curve of the base amplitude of the simulated particle-encapsulated hydrate layer with offset
层状模型3从上往下分别是海水层、饱水沉积层、含颗粒间胶结型水合物薄层、含游离气层和饱水沉积层(图5c)。低频(子波主频采用25 Hz)条件下,在3种介质分别模拟含游离气的颗粒间胶结型水合物薄层的正演结果。图12~图14分别展示了正演模拟得到的波场快照、单炮地震记录和含水合物层底界振幅随偏移距变化的关系。1)从波场快照(图12)可以看出,透射纵波在声波介质中传播时的能量最强,弹性介质中次之,双相介质中最弱。2)由地震记录(图13)可知,当含水合物沉积层的厚度较薄时,声波介质模拟含水合物层顶界的反射较为明显;在弹性介质中可以清晰地看到薄层顶底面的反射,且纵波走时相差很小,两种极性相反的同相轴相互干涉;而双相介质中能在含水合物薄层与含游离气层之间看到明显的负极性反射,却几乎看不到薄层顶界的反射。3)从振幅随偏移距变化的曲线(图14)可以看出,随着偏移距的增大,声波介质模拟薄层底界的振幅逐渐增大,而弹性介质和双相介质模拟的振幅都逐渐减小。
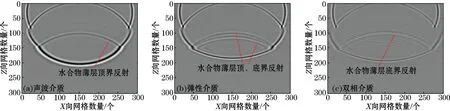
图12 模拟颗粒间胶结型水合物的网格化波场快照Fig.12 Snapshots of gridded wavefields that simulate interparticle cementation hydrates

图13 模拟颗粒间胶结型水合物的去除了直达波的单炮地震记录Fig.13 A single shot seismic record that simulates interparticle cementation hydrates with direct waves removed

图14 模拟含颗粒间胶结型水合物层底界振幅随偏移距变化的曲线Fig.14 The variation curve of the base amplitude of the simulated interparticle cementation hydrate layer with offset
将层状模型3(图5c)中含水合物薄层中水合物的类型改为颗粒支撑型后进行分析,得到高频(子波主频采用40 Hz)条件下,在3种介质中分别模拟含游离气的颗粒支撑型水合物薄层的正演结果(图15~图17)。1)从波场快照(图15)可知,在提高子波主频后,地震波形变窄。声波介质和弹性介质模拟水合物薄层顶底面的反射可以被区分。与之相比,双相介质模拟水合物薄层顶底界的反射能量要弱很多,不易被识别。2)从地震记录(图16)可知,声波介质和弹性介质模拟的水合物薄层出现了相互叠加的同相轴,但不影响薄层顶底面的识别。3)从振幅随偏移距变化的曲线(图17)可知,随着偏移距的增大,声波介质和弹性介质模拟薄层底界的振幅整体上逐渐减小,而双相介质模拟的振幅整体是增加的。与图12~图14相比,图15~图17中声波模型对水合物薄层顶底面的识别能力在高频条件下得以增强,弹性波模型识别水合物薄层的能力差别不大,而双相介质模型对其识别能力在高频条件下得以削弱。

图15 模拟颗粒支撑型水合物的网格化波场快照Fig.15 Snapshots of gridded wavefields that simulate particle-supported hydrates
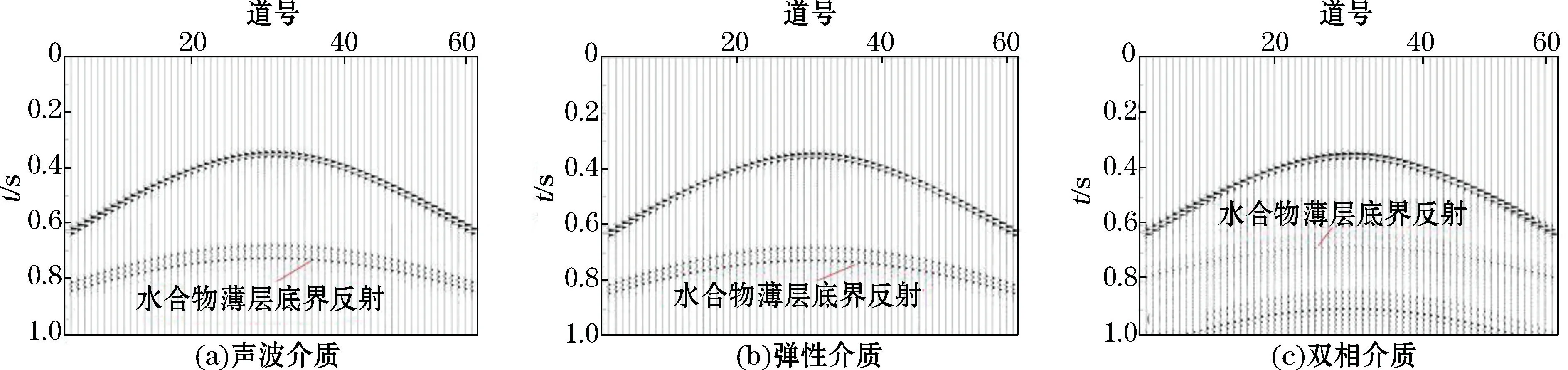
图16 模拟颗粒支撑型水合物的去除了直达波的单炮地震记录Fig.16 A single shot seismic record that simulates particle-supported hydrates with direct waves removed
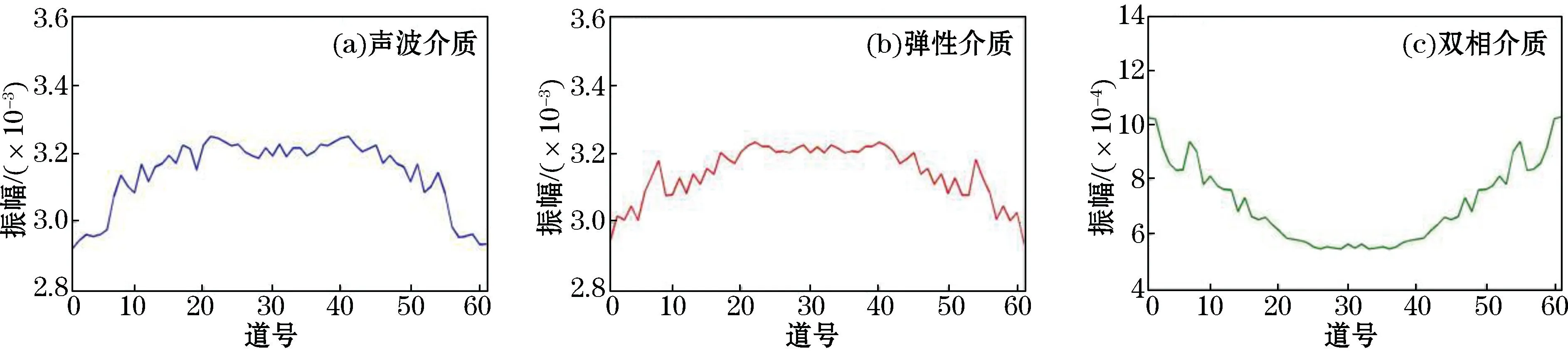
图17 模拟含颗粒支撑型水合物层底界振幅随偏移距变化的曲线Fig.17 The variation curve of the base amplitude of the simulated particle-supported hydrate layer with offset
层状模型4从上往下分别是海水层、饱水沉积层、含结核型水合物层和饱水沉积层(图5d)。低频(子波主频采用25 Hz)条件下,在3种介质分别模拟含结核型水合物沉积层的正演结果(图18~图20)。多个聚集成块状体的纯水合物(以下称“结核”)分布在沉积层中,形成多个波阻抗界面。1)从波场快照(图18)可知,3种介质模拟波场的能量大小关系和前文模拟的相似,在水合物结核处出现明显的振幅空白特征,主要是因为水合物结核内部阻抗差异较小,反射较弱;各种地震波之间相互干涉,波场异常复杂。2)从地震记录(图19)可知,由于水合物下部不存在游离气,声波介质模拟水合物底界的反射呈正极性,与图7a模拟的结果一致;弹性介质模拟水合物底界的反射呈负极性,这与图7b模拟的结果相反;双相介质模拟水合物底部的反射与弹性介质模拟的规律一致,与图7c模拟的结果相似。3)从振幅随偏移距变化的曲线(图20)可知,3种介质模拟水合物底界的振幅变化有着相似的规律,且除了双相介质模拟的在大偏移距处能量较小之外,其他位置基本一样。

图18 模拟结核型水合物的网格化波场快照Fig.18 Snapshots of gridded wavefields that simulate nodule hydrates
分析上述试验,对比结果见表4。其中,3种介质模拟水合物层底界的反射振幅大小整体高于10-3数量级的标记为强振幅,否则,为弱振幅。在利用声波介质与弹性介质模拟上层含20%水合物且下层不含游离气的波场时,孙小芳[36]发现含水合物层底界基本不产生负极性的BSR现象且振幅较小;相同的地质模型下,吴志强等[37]也认为很难看到明显的似海底反射现象。本文图6~图8中设定的地质模型和水合物饱和度与之相似,得到的试验结果也基本一致。当下伏介质含少量游离气且上层介质含适量的水合物时,含水合物层底界就会产生强振幅的负极性反射[36],与本文图9~图11中得到的试验结果基本一致。吴志强等[37]在研究水合物饱和度的变化对沉积层顶底界振幅的影响时,发现在其他条件相同的情况下,水合物饱和度达到40%以上将使含水合物层的顶界出现明显的反射。同时,该研究还认为提高子波主频对分辨薄层水合物十分有效。这两点在本文图12~图14和图15~图17的对比中都得到了验证。

表4 三种介质模拟不同类型水合物地震波场的对比Table 4 Comparison of three media simulating different types of hydrate seismic wave fields
4 结 论
本文总结介绍了天然气水合物在海洋中的6种主要赋存状态类型,概述了每种赋存状态之间的相互转化关系及其物性参数计算方法,并基于这些方法,求取了层状模型的各项参数。通过改变沉积层的厚度、子波主频信息,利用3种正演模拟方法对含不同赋存状态的水合物沉积层进行波场模拟,对比分析波场快照、地震记录的差异性,得到以下结论:
1)当地层中存在孔隙充填型水合物且下伏地层不含游离气时,声波介质和弹性介质模拟含水合物层底界表现出与海底反射极性相同的弱反射,而双相介质模拟含水合物层底界表现出负极性特征。当地层中充填结核型水合物且下伏地层不含游离气时,3种介质模拟水合物底界反射能量相近。声波介质模拟水合物底界依然表现出与海底反射极性相同的弱反射,而弹性介质和双相介质模拟水合物底界呈负极性。
2)当地层中充填颗粒包裹型水合物且下伏地层含游离气时,在低频条件下,3种介质模拟含水合物层底界的负极性反射明显;随着偏移距的增大,声波介质模拟水合物层底界的振幅先趋于稳定,后快速增大,而弹性介质和双相介质模拟的振幅呈震荡式变化。提高子波主频,地震波形较窄,水合物层底界反射依然明显。
3)当沉积薄层中充填颗粒间胶结型水合物且下伏地层含游离气时,不同于声波介质,弹性介质和双相介质模拟水合物薄层底界的反射振幅随偏移距的增大而减小;将水合物类型改为颗粒支撑型并提高子波主频,不同于双相介质,声波介质和弹性介质模拟水合物薄层底界的反射振幅较强,且随着偏移距的增大而减小。
本文使用的正演模型是二维各向同性的,而实际的地层情况较为复杂,建议将正演模型推广到三维的、各向异性的情况。同时,还需要不断优化算法,提高计算效率,设计更多符合实际地层的模型进行测试。文中的研究方法尚未对实际地层中的水合物数据进行应用,建议对实际数据进行应用,以利于后续研究。
