不同波纹倾角微型板片的传热与流动分析

2021-05-21于航韩向阳梁晓明

能源化工 2021年2期

于航，韩向阳，梁晓明

(青岛科技大学机电工程学院，山东青岛 266100)

计算流体力学Computational Fluid Dynamics(CFD)是可以通过使用计算机来求解流体力学控制方程并分析相应的流体力学问题，使用CFD 的方法研究板式换热器的板片得到越来越多的研究者的重视。

Patankar 等[1]使用CFD 的方法，对换热器进行了数值模拟研究和分析。Vafajoo 等[2]通过对波纹角度不同的人字板进行数值模拟，选择合适的波纹角度，大大了提高传热效率。Yoon 等[3]通过将通道节点和分支组成流动网格方法，对板式换热器进行数值模拟，结果表明优化入口流道设计可以提高精度。Kanaris 等[4]提出了板式换热器波纹的设计方法，数值模拟结果与已公布的结果一致。

Hu 等[5]用等雷诺数方法构建了试验装置，对由12 个人字板组成的6 个通道进行研究。袁俊飞等[6]发现微通道入口节流装置能够有效提高换热器的传热和流动性能。周正龙等[7]对微通道进行疏水性改造后，发现平均传热率明显提高。常宏旭[8]对设计的2 个微通道换热器可视化后，发现Z 型微通道的整体结构优于U 型微通道结构。张割等[9]对微通道水冷板进行设计和数值分析后，发现微通道与槽板相结合方法可以解决某些问题。吴秋瑜[10]通过数值模拟和试验比较了凹型和矩形微通道换热器，结果表明表面凹型微通道的传热性能良好。刘英楠[11]对平板微型通道的换热器不同长宽比进行模拟研究，结果发现当长宽比为1.67 时，平板微型通道的热交换性能最佳。

笔者主要通过数值模拟的方法，分析不同波纹倾角对微型板片传热和流动性能的影响，通过对努塞尔数的计算和分析建立了一种包含波纹倾角α的微型波纹板片换热准则方程。

1 建立几何模型

设计了一种微型波纹板片，结构示意见图1。

图1 波纹板片结构示意

图1 中选用的波纹倾角α为30°，45°，60°，70°，80°，波纹间距l 均为4.8 mm，波纹深度h 均为3 mm，模型尺寸均为100×100 mm，共5 组方案作为变量进行数值模拟研究。

首先用Solidworks 软件绘制出单张板片的物理模型，然后建立由5 片波纹板组成的四通道换热单元，四通道截面图见图2。微型波纹板片的网格图见图3，划分的板片网格数量见表1。

图2 换热板组结构示意

图3 网格示意

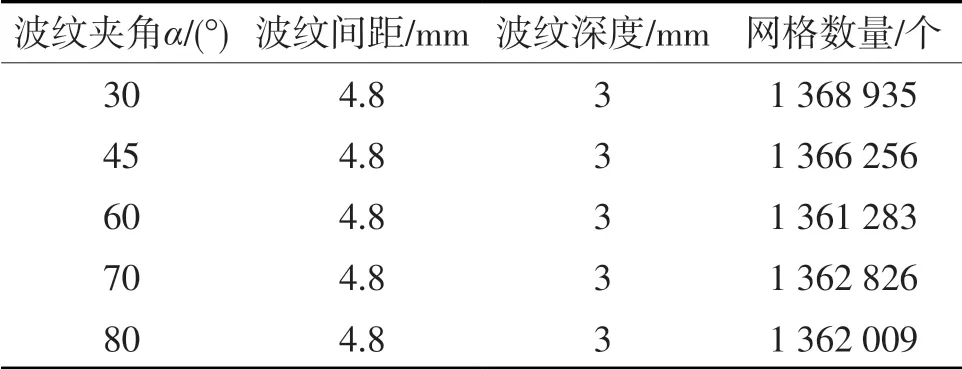
表1 不同波纹倾角α的板片网格数量

网格划分是数值模拟关键的一个重要计算步骤，网格划分中不同单元格的类型以及单元格大小等因素均会直接影响数值模拟运行时间及有计算结果[12]。选取非结构化的四面体网格对模型划分网格，网格数均大于100 万。网格数量变化对计算结果的影响见表2，其中j 为换热因子，f 为摩擦因子。

表2 网格变化数对计算结果的影响

由表2 可见：网格步长设定为1.5 mm，网格数约为136 万时，网格数对传热系数和摩擦系数影响不大，表明双通道冷热流体模型的网格密度能够满足模拟精度的需要。

2 控制方程及边界条件

2.1 数学模型

1)基本假设。波纹板片数值模拟过程中，板间介质没有发生相变，温度的变化也极小。因此在建立数学模型时作如下假设[13]：①工质的流动假设为定常流动；②工质流动时由黏性耗散相互作用产生的黏性耗散热效应忽略不计；③可视工质为不可压缩的黏性流体，工质在流道内的物性设为常物性；④忽略重力与浮升力的影响；⑤假设工质为均匀流动，忽略工质在流道入口的不均匀性。

2)控制方程。采用经典的连续性方程、动量及能量守恒方程，湍流模型选用Realizable k-ε模型。

2.2 边界条件

冷热工质流动示意见图4。冷热工质选择均为液态水，其物性参数见表3。

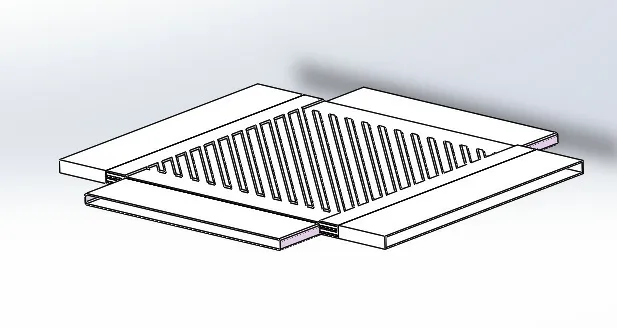
图4 流动示意

表3 冷热工质物性参数

在数值模拟计算过程中，冷、热工质入口边界均选为速度入口边界条件。入口边界处湍流的湍动为：

式中：k——入口界面处湍流动能，m2/s；——流体的平均速度，m/s；

I——湍流强度。

湍流强度公式为：

湍动耗散率为：

式中：ε——湍流耗散率，m2/s3；Cμ——经验系数，取值为0.09；

l——湍流尺度，m；

Ld——入口端特征尺度，m。边界条件见表4。

表4 冷热工质边界条件

通过数值模拟计算得到耦合边界条件中的波纹板表面换热系数、表面温度等值，其他设置为绝热壁面条件[14]。板片材料的物性参数见表5。

表5 板片材料的物性参数

2.3 求解计算

采用基于压力的分离求解器、SIMPLE 算法对压力进行修正和二阶迎风差分离散格式，收敛可信残差均值为1×10-5。

3 模拟过程及分析

在数值模拟结果数据处理中，用到如下几个物理量。

计算的板的非圆截面特征度为当量直径de，其计算方法为：

式中：a——板片通道长度，m；

b——板片间距，m。

努赛尔数Nu，在此次数值模拟过程中采用平均的Nu方法：

式中：q——平均壁面热通量，W/m2；

Tw——平均壁面温度，K；

Tf——流体平均温度，K；

λ——导热系数，kJ/(kg·K)。

3.1 不同波纹倾角微型板片的速度场分析

不同波纹倾角微型板片的速度场分析见表6。采用表4 的边界条件开展模拟研究，主要考察随着波纹倾角的不断增加，换热器内部冷、热侧流体流速变化情况。

由表6 可见：当波纹角逐渐增大至45°～ 60°时，流道方向切向力和流体流动方向是相互垂直的，流体会发生二次涡流，湍流度增强，传热效果明显增强，可以增强板式换热器的传热效果。当波纹角增大到70°时，湍流度减小，来自流道方向的切向力分量与流体流动方向相反，流体流动的转向点从波纹板边缘变为上板槽底与下板槽顶之间的间隙，形成一个小的波纹流，称为锯齿形流[13]。当α=80°时，流体流动模式是混乱的，流体只从几个流道流出。综上结果，当α=45°和60°时，流速相对均匀，传热效果较好。

3.2 不同波纹倾角微型板片的温度场分析

不同波纹倾角微型板片的温度场分析见表7。采用表4 的边界条件开展模拟研究，主要考察随着波纹倾角的不断增加，换热器内部冷、热侧流体温度场变化情况。

表7 不同波纹倾角微型板片的温度场

由表7 可见：当α=30°时，热侧波纹板的板间流速较小，流体流动不均匀，波纹角为30°时波纹板的温度场传热较差效果。当α=60°时，波纹板效果的传热效果最好。当α=70°时，由于流体的曲折流动，湍流度降低，流体流动变得不均匀，导致板片的传热效果降低较多。当α=80°时，流体流动板片的换热效果进一步降低。

3.3 不同波纹倾角微型板片的压力场分析

不同波纹倾角微型板片的压力场分析见表8。采用表4 的边界条件开展模拟研究，主要考察随着波纹倾角的不断增加，换热器内部冷、热侧流体压力场变化情况。

表8 不同波纹倾角微型板片的压力场

由表8 可见：当α=30°时，波纹板片流道沟槽的压力损失最小。当α=45°时，波纹板片流道沟槽的压力损失和换热的综合性能较好。当α=70°时，波纹板片流道压力损失进一步增大，是因为来自流道方向的切向力分量与流体的流动方向相反，这与流体在流道的运动状态相匹配。当α=80°时，波纹板片流道沟槽的压力损失最大。因此，在设计板式换热器时，应考虑传热与流阻的相关性，不应盲目追求较大的传热系数。

3.4 不同波纹倾角对换热强度的影响

不同波纹倾角对换热强度的影响见图5。

由图5(a)可见：雷诺数Re由500 升到3 500过程中，当α=30°时，Nu由27.64 增至149.54，增幅441%；当α=45°时，Nu从30.32 增至174.68，增大了5.7 倍。

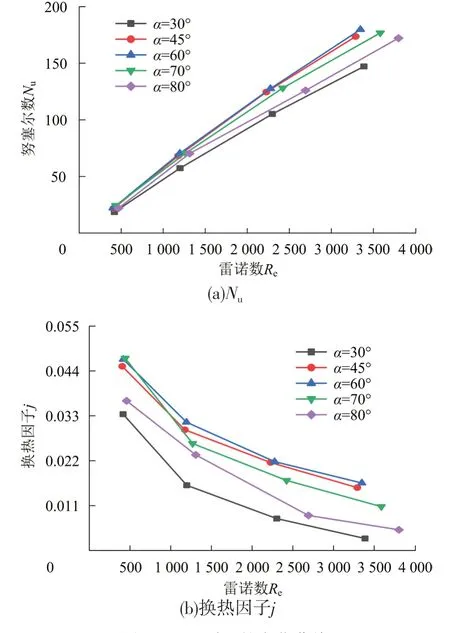
图5 Nu和j随Re的变化曲线

由图5(b)可见：当α=30°时，换热因子j 从0.042降到0.028；当α=60°时，换热因子j 从0.049 降到0.035；当α=80°时，换热因子j从0.043降到0.029。这主要是由于随着波纹角的增大，板间流体的流动状态由横流变为锯齿形流动。从换热效果方面考虑，波纹板片倾角应该选取α=45°或α=60°。

3.5 不同波纹倾角对流动阻力的影响

不同波纹倾角对流动阻力的影响见图6。

由图6(a)可见：当α=30°时，板片的压降从0.005 MPa 升至0.26 MPa，板片的压降增加了52 倍。当α=80°时，板片的压降从0.08 MPa 升至6.78 MPa，板片的压降增加了84.8 倍。表明大波纹角度的压降要比小波纹角度的压降增长倍数高很多，极高的压降也会带来更多额外的泵功，且对板片有冲击，影响板片的使用寿命。

由图6(b)可见：当α=30°时，板片的摩擦因子f 从1.39 降到1.05。当α=60°时，板片的摩擦因子f 从5.87 降到5.78。当α=80°时，板片的摩擦因子f 从20.76 升到27.65。仅从波纹板的阻力性能分析，波纹倾角小的热交换性能更好。

3.6 不同波纹倾角对面积质量因子的影响

面积质量因子j/f 的大小可以直接反映波纹板片传热和流动性能的综合质量，其数值越大，换热效果越好。不同波纹倾角对面积质量因子的影响见图7。

图6 Δp和f随Re的变化曲线

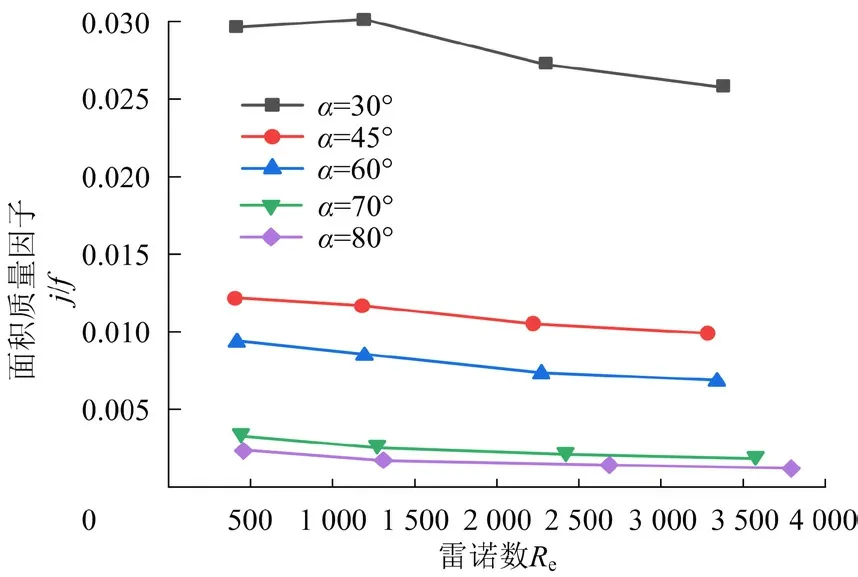
图7 j/f随Re的变化曲线

由图7 可见：当α=30°时，板片的j/f 数值从0.030降到0.026。当α=45°时，板片的j/f 数值从0.012降到0.01。当α=80°时，板片的j/f 数值从0.002 降到0.001，这主要是由于换热因子j 随着雷诺数不断减小而摩擦因子f 变化不大。从板片换热效果方面考虑，选取α=45°或者60°的波纹板片。综合j/f数值变化情况分析，则板片波纹角度选取45°。