自适应小波阈值滚动轴承故障振动信号降噪方法

纪俊卿，张亚靓，孟祥川，许同乐

(山东理工大学 机械工程学院，山东 淄博 255049)

0 引 言

在机械轴承的工作过程中，由于设备处于压力变化大、温差大和腐蚀气体含量高的特殊环境中，其机械轴承常常出现故障[1-3]。在仪器的检修过程中，轴承的振动信号通常比较微弱，且伴随大量噪音，传统的小波降噪方法不能满足提取轴承微弱故障振动信号的要求。采用合适的信号降噪的方法，对于机械轴承故障的预防检测起着关键作用[4-6]。

由于小波变换的降噪方法降噪能力差，Donoho、Johnstone等学者于1995年提出了一种通过小波阈值函数将含噪信号分解、重组的降噪方法，与小波变换相比，它能够更清楚的反映信号的非平稳变化的特性，提取其微弱的有效信号[7-10]。所提出的小波降噪方法有两种：硬阈值法和软阈值法。而硬阈值法和软阈值法分别有存在间断点、与原信号相比有恒定误差的缺点，有效特征不明显，并不能满足如今信号处理分析的要求。国内有许多学者针对软硬阈值的缺点对其进行改进，但由于缺少灵活因子，适应性较差以及偏差较大等问题，降噪效果并不理想。比如有的学者[11]为了克服传统方法的缺点，在半软阈值的基础上提出新的阈值函数，但新阈值降噪的信号仍含有一定程度的误差；文[12]以软硬阈值为基础，提出一种改进阈值来解决传统方法存在问题，但由于每一层分解阈值固定不变，在一定程度上限制了算法的灵活性。

对于不同噪声的适应能力不强，降噪能力不高。针对上述降噪方法所存在的问题，本文在传统阈值函数的基础上提出一种自适应小波阈值函数。通过相关系数对新的小波阈值进行优化，同时提出一种自适应小波阈值函数，既能够有效的克服不连续的缺点，还可以解决降噪信号与原信号含有误差的问题，实现对采集信号的降噪，最大化的保持有效信号的特征。

1 传统小波阈值降噪

在信号降噪处理的领域中，实际上可以将小波阈值函数降噪表示为一个滤除噪声、提取有效信号的过程。小波阈值降噪就是通过对含噪信号的分解重组，将主要集中在高频小波系数的噪声滤除，提取出存在于低频小波系数的振动信号[13]。因此，小波降噪的核心就是对被测振动信号滤波与有效特征提取相结合的一个过程。

1.1 小波阈值理论

传统的小波阈值降噪过程为：首先给采集的轴承振动信号选择适当的小波阈值函数以及最大小波分解层数，根据小波阈值函数计算出每层的小波系数；其次将传统的阈值函数量化，计算出估计小波系数；最后通过每一层的小波系数和估计小波系数将分解后的信号重新组合，得到处理后的信号，实现降噪处理[14]。

1.2 传统小波阈值降噪的方法及其不足

在液压系统机械轴承的信号采集过程中发现，噪声信号大多数出现在高得小波系数中，而有效信号通常分布在低的小波系数中，硬阈值和软阈值降噪法可以很好的滤除噪音，但同时对有效信号产生影响。

1.2.1 硬阈值降噪法

首先，将阈值函数η初始化，并与小波系数wj,k进行对比，如果|wj,k|≥η，那么保持原有阈值函数；相反的，如果|wj,k|<η，将其置零[15]。该原理表示为:

1.2.2 软阈值降噪法

将阈值函数η初始化，并与小波系数wj,k进行对比，如果|wj,k|≥η，那么更新后的小波系数为|wj,k-η|；相反的，如果|wj,k|<η，将其置零[16]。该原理表示为

2 自适应小波阈值函数降噪方法

2.1 自适应小波阈值

对于传统的小波阈值处理振动信号的方法，是否能够选取合适的小波阈值将直接影响处理精度[17-22]。若选择的小波阈值过大，可能将信号当中的有效信号和关键信号滤除，有效特征不明显，不能保留信号的原始特征；反之，如若选择的小波阈值过小，信号中的干扰不能充分滤除，导致信噪比较低。

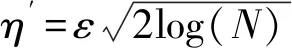
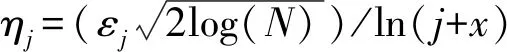
其中：x为调节参数；εj为均方根误差，通常ε=median(|Wj,k|)/0.674 5，median(*)为计算中值；N为信号长度。

假设原始的一组数据为a1=[a11,a12,…，a1n]T，以及每层分解后的一组数据a2,j=[a21,a22,…，a2n]T，将每层小波阈值分解后的信号与原信号进行相关系数r1,2的计算，其中r1,2表示为：

其中：Cov(a1,a2,j)为a1,a2,j的样本协方差；Var(a1)Var(a2,j)为a1,a2,j的样本方差。且|r1,2|≤1。

综上，小波在进行每一层的分解得到的数据与原始数据相关性不同，小波阈值相应的取值也有所不同，根据相关系数自适应的选取小波阈值，提高算法的适应性。

2.2 自适应阈值函数的提出

对于上述小波阈值存在的问题，提出了一种自适应小波阈值函数的信号处理方法。自适应阈值函数如下：

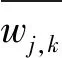
2.3 自适应阈值函数的理论分析

1)连续性

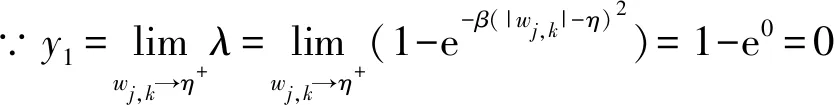
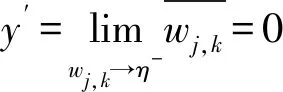
所以，由上述推导可知，自适应阈值函数在±η处连续，克服了硬阈值函数的问题。

2)偏差性

同理：

wj,k)=0

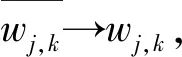
3)阈值调节因子的分析

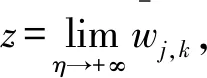
ⅱ)当β→+∞,那么λ=1-e-β(|wj,k|-η)2=1-e-∞=1，将λ=1带入z可知：当wj,k≥η时，z=wj,k，相反，z=0。

由上式可知该阈值函数能够完成从硬阈值与软阈值相互转化的过程，能够对不同工况下的信号进行降噪处理，极大地克服渐进半软式阈值和改进指数阈值函数的问题，增强降噪能力。图1为新阈值与软硬阈值降噪曲线对比。

3 仿真分析及实验验证

本次实验对轴承故障振动信号进行故障诊断和分析，通过对故障信号的频域以及频域信号的细化谱的对比，分析本文算法的降噪性能。其中，实验用到的数据为美国凯斯西储大学采集的轴承振动数据，其型号为6205-2RS型。基本参数如表1所示。图2、3、4分别为振动故障信号降噪流程图、不同阈值函数的频域信号和频域信号的细化谱。

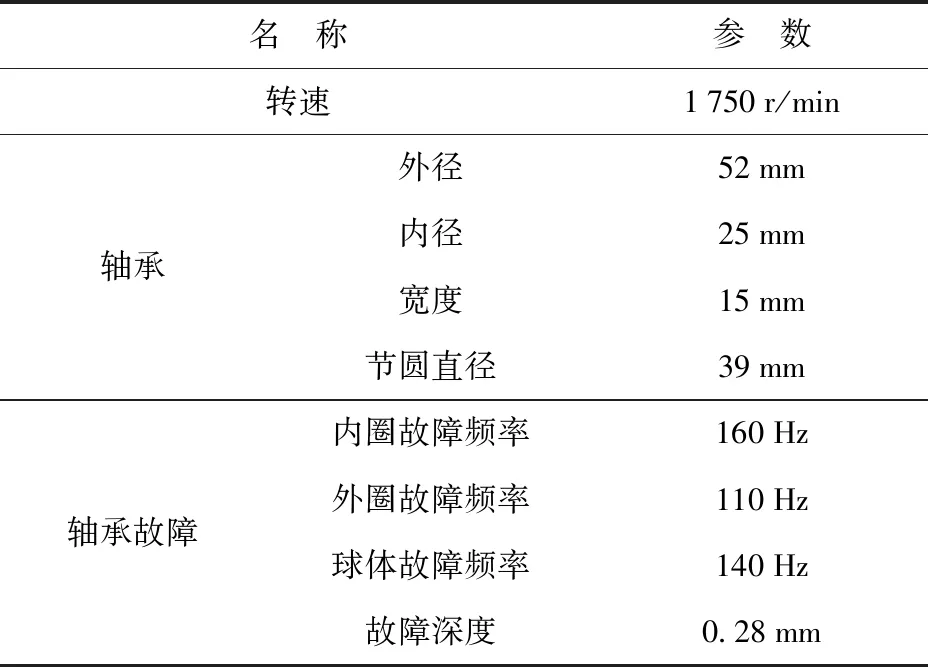
表1 轴承规格参数与故障频率参数

图2 振动故障信号降噪流程图Fig.2 Noise reduction flow chart of sinusoidal signal with noise

具体的仿真流程为：

1)首先根据轴承运行工况确定最大分解层数i，将待测信号进行分解；

2)每层分解后得到的数据，都要与原始数据进行相关性分析，得到相关系数的r1,2，进而选择合适小波阈值η；

3)计算出信噪比SNR和均方差MSE，并输出分解后的波形；

4)随后分别利用不同阈值函数对阈值大小进行计算，最终将经过阈值处理后的小波系数进行重组，并将经过各阈值降噪的波形进行对比分析。

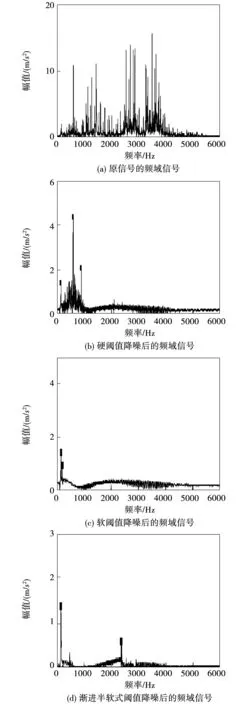
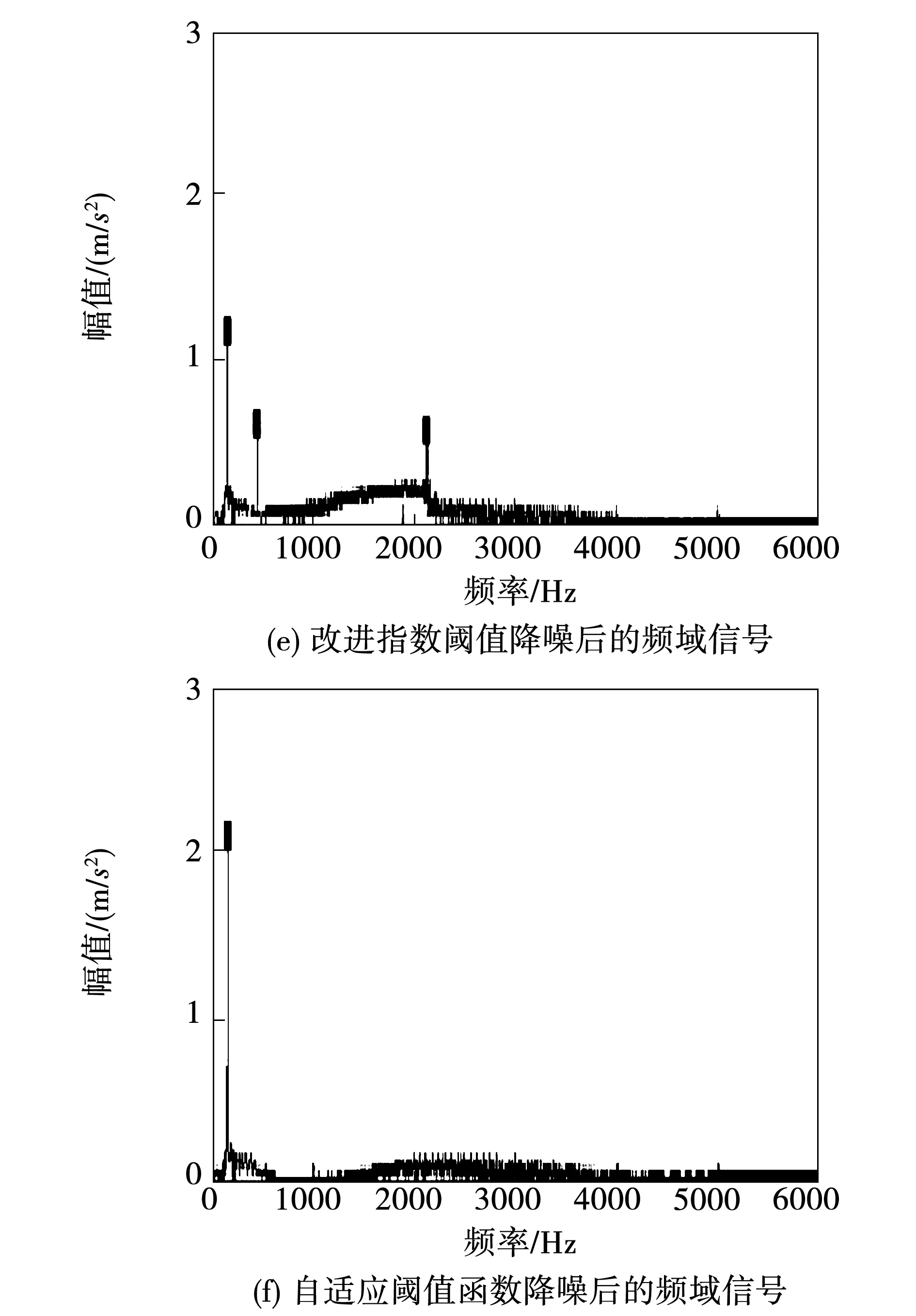
图3 不同阈值函数降噪处理的频域信号Fig.3 Frequency domain signals with different threshold functions for noise reduction

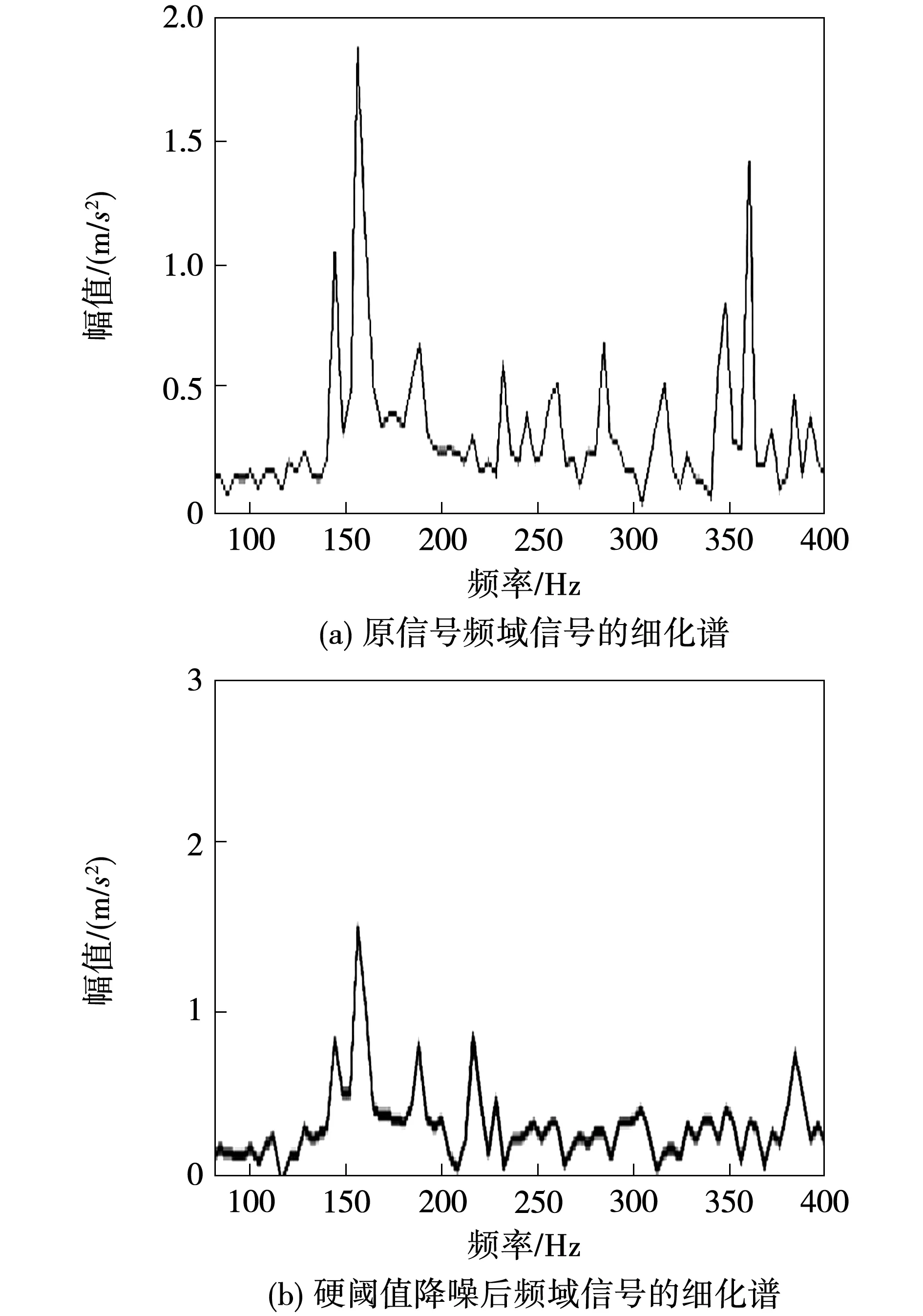
图4 不同阈值函数降噪处理频域信号的细化谱Fig.4 Refinement spectrum of frequency domain signal with different threshold function noise reduction processing

由图3、4中可以得出以下结论：

1)通过从硬阈值处理后的频域信号及其细化谱来看，虽然在一定程度上滤除噪声，但是能量分布并不集中，如在频率0～1 200 Hz内噪音较大，而在细化谱中几乎所有显示的频率段上都含有噪声，不能将有效的故障信号提取出来；

2)软阈值函数处理过的待测信号，虽然滤除掉一部分噪音，但是破坏了原信号的有效特征，造成有效信息的丢失，这一点通过频率谱就可以看出，图中几乎没有峰值，也就是将有效信号的关键特征滤除掉了；

3)经过渐进半软式阈值和改进指数阈值降噪后的频谱图以及频谱细化图可以看出，虽然降噪性能较好，但是由于有效特征提取不够完整且峰值出现没规律，所以不能够快速、准确地判断出现故障的类型；

4)经过自适应阈值降噪的频谱以及细化图分析来看，可以看出降噪比较彻底，且只在频谱信号细化谱的160 Hz处都有峰值，通过表1可以得出待测故障为轴承内圈故障。本文分别计算了3种不同的阈值函数的信噪比(SNR)和均方根(RMSE)误差。表2、3、4为不同小波阈值算法降噪效果的对比。

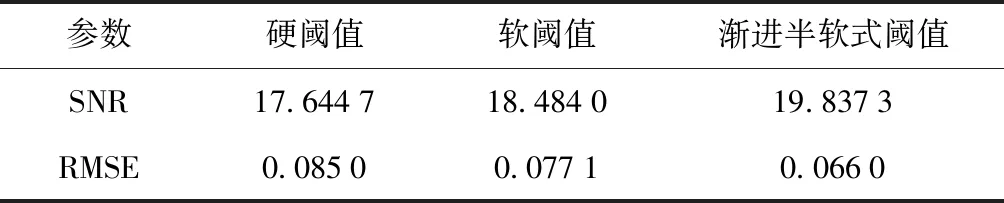
表2 渐进半软式阈值与传统降噪方法对比

表3 改进指数阈值与传统降噪方法对比

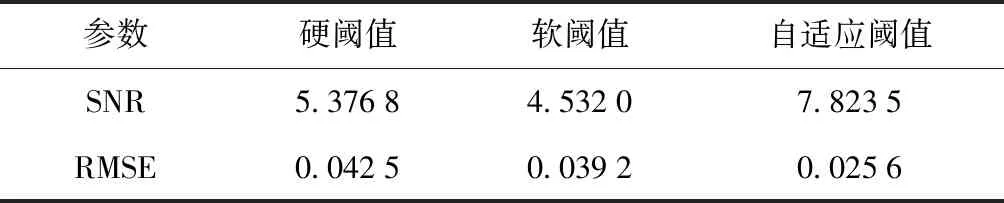
表4 自适应阈值与传统降噪方法对比

通过表2、3、4观察得出，本文所提出自适应小波阈值方法与渐进半软式阈值和改进指数阈值相比，MSE更小，SNR更高，且能够适应不同工况下的轴承故障特征的提取。

4 结 论

本文研究了一种自适应阈值函数勇用于不同工况下的轴承故障信号的提取，通过以下三点，说明自适应阈值算法能更好的提取机械轴承振动的微弱信号。

1)通过理论分析可以得出，自适应小波阈值克服了硬阈值不连续的问题，并且减少降噪后的信号与原信号的恒定偏差。利用改变调节因子实现新阈值函数在软、硬阈值函数之间过渡转化，灵活性好，适应能力强；

2)通过对轴承振动信号的时、频域以及频域信号的细化谱分析可知，自适应小波阈值方法对原始信号的降噪更为彻底，能量更为集中，幅值变化更为明显、规律，通过计算，迅速确定轴承的故障类型，能够更好的对液压系统的机械轴承故障进行排查、处理；

3)本文通过对软阈值和硬阈值以及现有的阈值降噪方法MSE和SNR的对比，本文所提出的阈值降噪方法SNR更高，MSE更低，能够更好的提取微弱的有效信号，优化降噪性能。