基于链导法则的梁弯曲变形的精确分析

张晓晴，刘 晗，许银胜，李志强

(1.华南理工大学 a.土木与交通学院，b.机械与汽车工程学院，广州 510641； 2.太原理工大学 机械与运载工程学院，太原 030024)

结构设计中的基本要求是结构安全性[1-2]，安全性主要由结构中的各个构件体现，常见的构件为梁和柱。结构安全性主要包括结构的强度和刚度。在结构设计的过程中，强度往往有精确的计算方式，而刚度的计算方式——挠曲线方程，是在忽略一些高阶微量的条件下得到的近似方程。周根华等[3]基于近似挠曲线方程，建立了常用载荷作用下梁的转角方程与挠曲线方程用挠曲线增量表示的解析式。赵红华等[4]基于分析梁在偏心轴力、剪力作用下挠度曲线得到的挠曲线方程，推导出反映弯曲、剪切、扭转、翘曲和P-δ效应的相互影响的刚度矩阵。可见挠曲线方程在基础力学研究中的重要地位，推导出更加精确的挠曲线方程具有一定的实用价值。

国内学者针对近似挠曲线方程做了一些研究改进，张世杰[5]用待定系数法求梁在集中载荷作用下的挠曲线方程；刘明超等[6]利用拉氏变换求解梁的挠曲线方程；刘海波等[7]在不忽略任何高阶微量的基础上，对挠曲线函数进行了精确推导，增加了刚度计算的精度，但也存在忽略链导法则引入的高阶微量的情况。基于此，为了进一步对梁弯曲变形进行精确分析，本文不采用其他学者忽略部分微量进行近似分析的方式，而考虑链导法则引入的高阶微量，从几何特性和微量关系出发，降低和消除梁弯曲变形推导过程产生的误差，得到精确转角函数，并在精确转角函数的基础上，得到精度更高的梁位移函数。

1 传统梁挠曲线近似方程

梁刚度主要包括转角和挠度两部分，国内外绝大多数材料力学教材中[8-11]对挠曲线近似函数的描述为：

(1)

式中：M(x)为梁的弯距；E是梁的弹性模量；I是弯曲轴的惯性矩。

将式(1)左右两边同时积分，得转角函数：

(2)

其中θ(x)为梁的转角。对式(2)左右两边同时积分，得到挠曲线近似函数：

(3)

通过两次积分最终得到挠曲线近似函数，在转角较小时，通过式(3)计算得到的误差较小，但是在转角较大时，其误差可达10%.在实际工程中使用时，特别是结构荷载较大时，式(3)的使用有较大的局限性，所以有必要对转角函数和梁变形位移函数进行精确推导。

2 基于链导法则的精确推导过程

链导法则是求复合函数的导数或偏导数的法则，其定义为：

若I，J是直线上的开区间，函数f(x)在I上有定义且在a点(a∈I)可微；函数g(y)在J上有定义(J⊃f(I))且在f(a)处可微，则复合函数(g°f)(x)=g(f(x))在a点可微(由上述条件易得g°f在I上有定义)。

若记μ=g(y)，y=f(x)，又因为f在I上可微，g在J上可微，所以易得(g°f)′(x)=g′(f(x))f′(x).

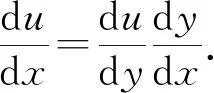
利用链导法则，可以对梁弯曲变形做精确推导，即考虑链导法则引入的高阶微量，进一步提高精度，过程如下：

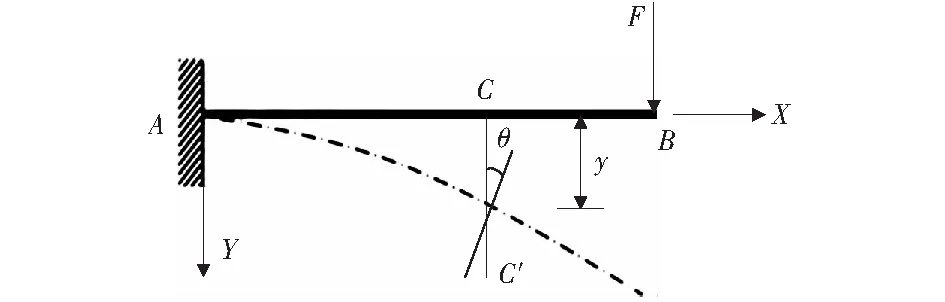
图1 梁受弯形变示意图[6]Fig.1 Bending deformation of cantilever beam

如图1所示，为了简化推导过程，利用悬臂梁模型进行推导，该悬臂梁左端为固定约束端，右端为自由端，在B端仅受一竖直下的力F，梁受力后弯曲至图中虚线位置。图中虚线即为挠曲线f(x)，θ(x)即为所求的梁弯曲转角函数，以向右为x轴，向下为y轴建立坐标系。通过几何关系可得，θ(x)实际上也为挠曲线上一点的切线与过该点的水平直线所成的锐角，根据求导的定义可得：

f′(x)=tan(θ(x)) .

(4)

由于曲率和梁的弯矩存在下列关系：

(5)

式中：ρ(x)为曲率半径；M(x)为梁的弯矩；E是梁的弹性模量；I是弯曲轴的惯性矩。需要注意的是，M(x)可能为常函数，但M(x)始终存在连续可导的区域，此处推导忽略了M(x)上的奇点情况。

在数学几何上，存在下式：

(6)

对式(4)左右两边同时对x求导得：

(7)

利用链导法则进一步化简得：

(8)

化简得：

(9)

将式(4)、式(9)代入式(6)中得：

(10)

因为1+tan2[θ(x)]=sec2[θ(x)]，所以式(10)可以化简为：

(11)

联立式(5)和式(11)得：

(12)

式(12)等号两边同乘dx得：

(13)

式(13)等号两边同积分得：

(14)

化简得：

(15)

所以精确的转角与弯矩函数间存在下列关系：

(16)

式(16)中的正负号仅用以保证等号两边的符号相同，对比式(16)与式(2)，不难理解在转角较小时，sinθ(x)和θ(x)十分接近，此时使用式(2)进行计算得到的结果误差较小，但随着转角的增大，sinθ(x)和θ(x)的差值增大，此时使用式(2)计算所得的结果就与实际情况相差较大。式(16)等价于：

(17)

式(17)即为精确的梁弯曲转角函数。对于任意非纯弯曲的受弯梁，其精确转角都可以用式(17)求得；同时，若给定材料的几何尺寸、弹性模量和加载位置和加载方式，可以通过式(17)初步确定荷载的上限，具体如下：

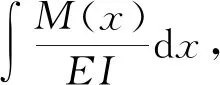
3 基于精确转角函数的挠度函数

由于式(17)所求出的弯曲转角的精度较高，在式(17)的基础上得到的近似挠曲线方程较传统挠曲线方程的精度也会相应提高。即：

(18)

式(18)的计算十分复杂，可利用相关软件求得数值解。式(18)的推导中运用了近似，若利用式(17)依据dx，θ，dθ的几何关系，可以精确推导出梁的挠曲线方程，但是精确的挠曲线方程形式十分复杂，相关内容将会在后续研究中进行。

4 有限元分析

利用ANSYS参照图1建立悬臂梁模型，有限元模型的相关参数如表1所示。

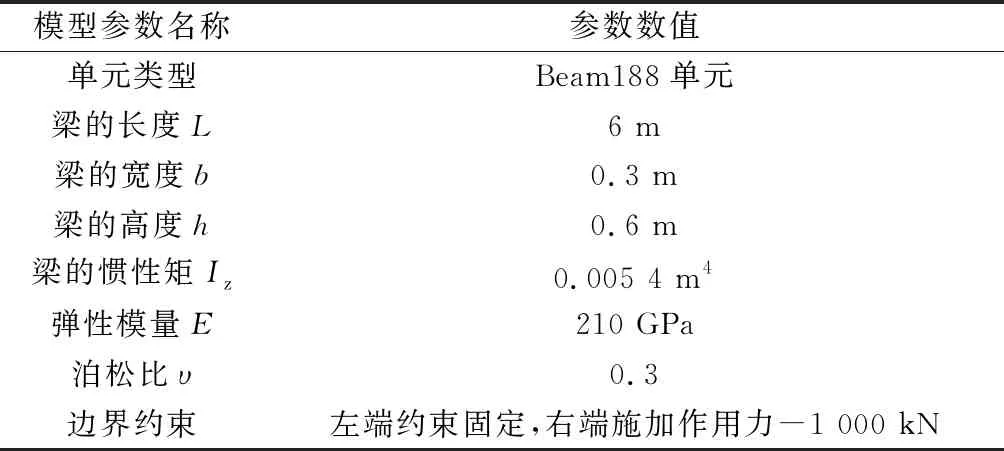
表1 有限元模型相关参数Table 1 Relevant parameters of the finite element model

按照表中的边界约束条件在ANSYS中对悬臂梁模型施加载荷，求解得到梁上6点的转角和挠度。如图2为悬臂梁模型的节点分布，如图3为悬臂梁各节点处的转角结果，如图4为悬臂梁各节点处的挠度结果。

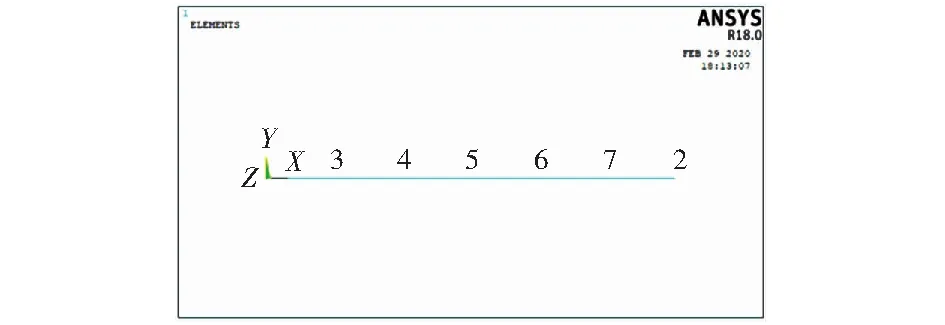
图2 悬臂梁节点分布Fig.2 Cantilever node distribution

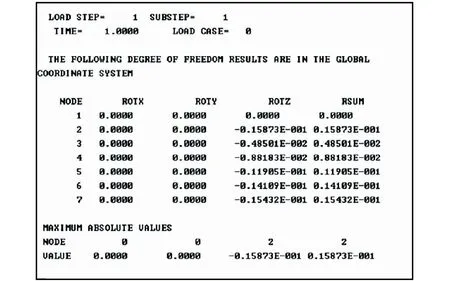
图3 悬臂梁各节点处转角结果Fig.3 Rotation angle at each node of the cantilever beam

5 结果分析

依照式(17)写出梁的精确转角函数，利用精确函数计算转角和挠度，具体过程如下：

M(x)=-Fx+FL=-1 000x+6 000 .

(19)

所以转角和挠度分别为：

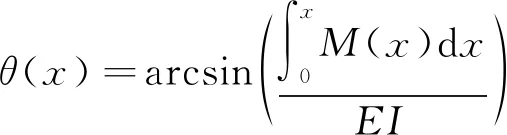
(20)

(21)

(22)

利用式(21)-(22)计算梁上6点的转角和挠度值，结果如表2所示。

表2 精确函数计算的各节点转角和挠度值Table 2 Each node’s angle of rotation and deflection by the precise function

为了更加直观地观察本文所述精确转角函数的精确性，将运用本文所述精确转角函数计算出的悬臂梁各节点处转角结果与有限元软件分析得出的转角结果绘制于同一坐标图中，如图5所示。

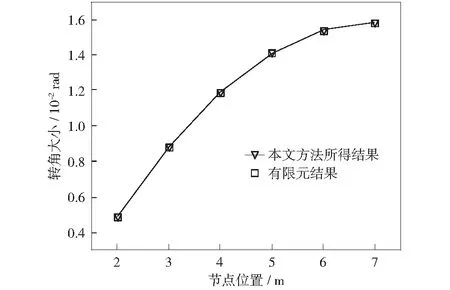
图5 悬臂梁各节点处转角结果不同方法对比Fig.5 Comparison of rotation angle results at each node of cantilever beam by different methods

将运用本文所述精确转角函数计算出的悬臂梁各节点处挠度结果、有限元软件分析得出的挠度结果和其他学者所述方法计算出的挠度结果绘制于同一坐标图中，如图6所示(以梁向下弯曲变形的挠度值为正方向)。

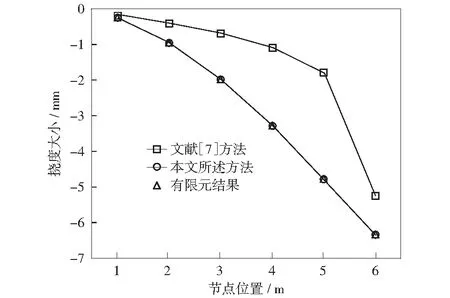
图6 悬臂梁各节点挠度结果不同方法对比Fig.6 Comparison of cantilever beam deflection results by different methods

将图4中运用本文方法所得结果与有限元转角结果对比可得，精确转角函数计算的结果与有限元结果十分接近，误差在1%以内，可以说明精确转角函数的精确性。从图5可得，基于精确转角函数推出挠度函数的计算结果与有限元仿真结果相比，误差在3%以内，而采用传统近似函数，最大误差接近10%[7]；且采用本文方法计算的挠度结果相较于文献[7]所述方法计算得到的结果更接近于有限元仿真结果。

通过对比可以说明，利用精确函数计算得到的挠度结果，其误差降低、精度提高，并且当梁上荷载增大时，传统近似函数的误差普遍增大，此时精确函数的结果仍具有相当高的精度，误差范围基本在1%～3%之间，可满足实际工程的设计要求。

6 结论

1) 精确转角函数与挠度函数符合实际且计算精度较高，可以用于实际工程，利用相关软件可以快速地得到计算结果，可用于设计辅助软件的开发，拥有广泛的应用前景。

2) 通过考虑链导法则引入的高阶微量，明显降低转角和位移误差，并且在梁上荷载增大时，精确函数仍具有较高精度，而传统公式误差偏大。

3) 精确函数的推导过程侧面证明了传统公式的可行性，同时解释了在荷载增大导致梁转角增大时，传统公式误差增大的原因。

4) 利用精确转角公式可粗略估计结构上外加荷载的上限，为加载试验提供参考。