NRS-SVM两阶段遗传算法的多晶硅铸锭配料质量分析

徐静林，黄丽霞，张雪英，李凤莲，杜海文，于丽君，马 秀

(1.太原理工大学 信息与计算机学院，太原 030024；2.山西省中电科新能源技术有限公司，太原 030024)

随着光伏行业的迅猛发展，多晶硅电池凭借其较高的性价比一直占据着光伏市场的主导地位[1]。铸造多晶硅是多晶硅电池制作过程中的一个重要环节，提高多晶硅的铸造质量是保证电池质量的关键。目前多晶硅铸造生产工艺已经相对成熟，所以生产工艺对最终多晶硅生产质量的影响相对较小，而配料在高效多晶硅铸锭生产过程中起着决定性的作用，对高效多晶硅铸锭的电学性能有着至关重要的影响，同时有效合理的配料工艺对成本也有着关键性的影响。所以，对多晶硅铸锭配料数据的分析有较大的工业价值。

20世纪80年代以前一般都是靠人工对多晶硅铸锭质量进行分析，这种方法效率低且准确率不高。随着大数据技术的发展，许多新的数据分析方法开始用于工业生产中。例如文献[2]利用核主元分析(KPCA)提取特征向量，将提取后的主元作为SVM的输入，对故障进行诊断和分类。文献[3]提出一种DB小波与RBP神经网络的方法对短期电力负荷预测，但训练样本过大时，训练速度会很慢。文献[4]提出将邻域粗糙集与支持向量机结合，进行固结系数预测，减轻了SVM的训练负担，但由于实际数据中，数据变化较大，邻域半径取值及分类器参数基本是凭经验和反复实验来确定，所以如何准确快速得到邻域半径及SVM分类器中惩罚系数c与核函数参数g的取值，在工业生产分析的实用性方面有很大的研究意义。基于以上分析，本文提出一种邻域粗糙集-支持向量机模型与遗传算法相结合的两阶段遗传算法(NRS-SVM-GA)，该算法通过遗传算法优化NRS-SVM参数，并将遗传算法分两个阶段进行，根据每个阶段的目的提出相应的适应度函数及终止条件。第一阶段在代数观点下的邻域近似质量和约简集合长度基础上，提出了新的约简性能评价函数，并将其作为遗传算法第一阶段的适应度函数，通过搜索邻域半径参数得到该适应度函数下最佳的约简集合；其次，在SVM的分类精度及第一阶段约简结果基础上提出第二阶段适应度函数，通过调整惩罚系数c及核函数参数g训练出准确率较高的分类模型。该方法不仅克服了以往根据经验或实验选择参数的弊端，而且避免了通过分类器来评价约简性能所带来的时间消耗，且实现了NRS-SVM快速自动化特征提取及分类预测。

1 相关原理简介

1.1 邻域粗糙集理论

粗糙集作为一种属性约简方法，能够有效地分析低维且不完备的工业生产数据。但Pawlak粗糙集定义在经典等价关系和等价类基础之上[5]，只适合处理名义型变量，对于实际生活中普遍存在的数值型变量却不能直接处理。胡清华等[6]将邻域概念引入到粗糙集中，克服了经典粗糙集不能直接处理数值型数据的缺陷，但邻域半径的取值一般采用经验值或者通过反复实验获得，极大限制了工业应用的自动化程度，且会导致输出结果不稳定。因此，本文对邻域半径参数进行优化，提高其在工业应用中自动化程度。邻域粗糙集相关原理如下：

给定一个邻域决策系统NDT(U,C∩D,V,f)，其中U为对象的非空无限集合，称为论域，C为条件属性，D为决策属性，V为各属性值的集合，f是信息函数，表示样本、属性和属性值之间的映射关系。

定义1[6]对于任意的xi∈U，B⊆C，xi在属性子集B上的σ-邻域定义为：

σB(xi)=|xjxi∈U，ΔB(xi,xj)≤σ| .

(1)

式中：σ≥0，ΔB为两样本点之间欧式距离。

由于在实际工业生产中，决策属性大多都为数值型数据，在进行属性约简时仍需将其离散化处理，本文将邻域粒度概念扩展到决策属性中，重新定义了论域U对决策属性D的划分，这样不需要再对数值型决策进行离散化处理，且相比离散化处理细化了决策对论域的划分。

定义2 给定一个决策系统NDT(U,C∩D,V,f)，xi在决策属性D上的决策划分情况为：

D(xi)=|xixi∈U,ΔD(xi,xj)≤σ| .

(2)

定义3 给定一个决策系统NDT(U,C∩D,V,f)，B⊆C生成U上的邻域关系NB，σB(xi)表示对象xi在属性B下的邻域，决策属性集D关于条件属性B的下近似和上近似分别为：

NBDi=|xiσB∈Di,xi∈U| .

(3)

(4)

那么数据的边界域定义为：

(5)

定义4[7]给定一个决策系统NDT(U,C∩D,V,f)，对∀B⊆C，决策属性D关于条件属性B的邻域近似质量可以定义为：

(6)

式中：正域POSB(D)=NBD.

1.2 支持向量机理论

支持向量机作为一种有效的分类模型，可以在一定程度上检验邻域粗糙集属性约简结果的可靠性，且常作为属性约简评价指标之一。其原理是先将所有的训练向量映射到一高维空间中，然后在这个空间中构建一个最大间隔超平面。支持向量机的核函数主要分为4种：线性核、RBF(radial basis function，径向基)核、多项式核和Sigmoid核。本文采用RBF核。

如果要构建一个SVM，就需要先选择SVM的惩罚因子c及核函数参数g.惩罚因子c控制学习复杂度，理论上随着c的增大复杂度逐渐增高，但当c大到一定程度，超过空间复杂度的最大值时，对支持向量机的性能就不会再产生影响。核函数参数g的改变实质上是支持向量机向高维度投影的特征空间的复杂度改变，当核参数增大时，投影空间复杂度降低，线性可分程度也降低；而当核参数趋于0时，特征空间的复杂度会趋于无穷，此时虽然将任意数据映射为线性可分，但会造成过拟合现象。因此需要针对数据集设置合理的惩罚因子c及核函数参数g，从而获得较好的分类效果。但在实际工业数据分析中，对于参数c、g的寻优会耗费大量时间，影响分析效率。本文针对属性约简后的多晶硅配料数据，对SVM参数进行优化，减少其训练时间。

1.3 NRS-SVM模型标准遗传算法

NRS-SVM模型已经广泛应用于数据的特征提取及分类预测[8]，虽然目前针对SVM参数寻优问题已有相对成熟的寻优算法，但对于邻域半径参数往往使用经验值或者多次试验获得，最终通过对比不同邻域半径取值下分类器的分类精度来得到相对较好的邻域半径取值，这样会造成大量由分类器所带来的时间消耗，同时也极大限制了工业应用中NRS-SVM的自动化程度。NRS-SVM模型标准遗传算法通过分类器分类精度及约简集合长度来综合评价约简性能，当搜索邻域半径取值时会产生多个约简结果，需要对每个约简结果都进行分类，产生巨大时间消耗。因此，本文提出NRS-SVM两阶段遗传算法。

2 NRS-SVM两阶段遗传算法

针对NRS-SVM模型参数问题，采用遗传算法对其进行参数寻优。遗传算法(genetic algorithm，GA)起源于对生物系统研究的计算机模拟研究，是模拟生物界遗传形式和参考生物进化理论而形成的一种可以并行随机搜索的优化方法，它把自然界生物自然选择优秀个体的方法引入到优化参数问题形成的串联编码群体中，参照自然界适者生存的选择办法，按照所选择的适应度函数对个体进行测试和选择，通过选择、交叉和变异等步骤对个体进行筛选，使适应度好的个体得以保留[9]。近年来，遗传算法作为一种模拟生物进化和遗传规律搜索寻优方法，具有通用性强、全局最优、搜索速度快等优点，目前已成为解决各种复杂问题的有力工具[10]。

本文提出基于NRS-SVM的两阶段遗传算法(NRS-SVM-GA)，即采用两个阶段标准的遗传算法，每个阶段的不同在于适应度函数和终止条件设置不同。第一阶段的目的是寻找到较优的约简集合，第二阶段的目的是训练出准确率较高的分类模型。这样，第一阶段通过搜索最佳邻域半径参数λ(本文采用标准差下的邻域半径δ=Dst/λ)来保证数据较高的邻域近似质量和相对较少的配料特征个数，进而将第一阶段约简结果作为第二阶段SVM的输入。由于以往都是通过分类器下的分类精度来评价约简性能，而本文第一阶段属性约简的适应度函数没有用SVM分类精度作为约简性能评价指标，所以不用再对第一阶段得出的每个约简集合都进行SVM分类，极大减少了运算量；第二阶段直接使用第一阶段的约简结果，通过搜索最佳惩罚因子c及核函数参数g来训练出较高的分类模型。算法流程如图1所示。算法中各参数设置如表1所示。

2.1 适度函数

2.1.1第一阶段适应度函数

适应度函数为两阶段遗传算法的核心部分，一个好的适应度函数既可以满足所要达到的目的，同时也可以减少算法的复杂程度。本文所提算法NRS-SVM-GA中，第一阶段的目的是通过寻找最佳邻域半径来准确地刻画基本信息粒子，从而保证数据较高的邻域近似质量且保留相对较小的约简集合，由式(3)-式(6)可看出，较高的邻域近似质量可以保证数据较高的正域，正域越大，边界域越小，知识的不确定性越小，数据的分类性能就越好。根据以上目的，提出第一阶段适应度函数：

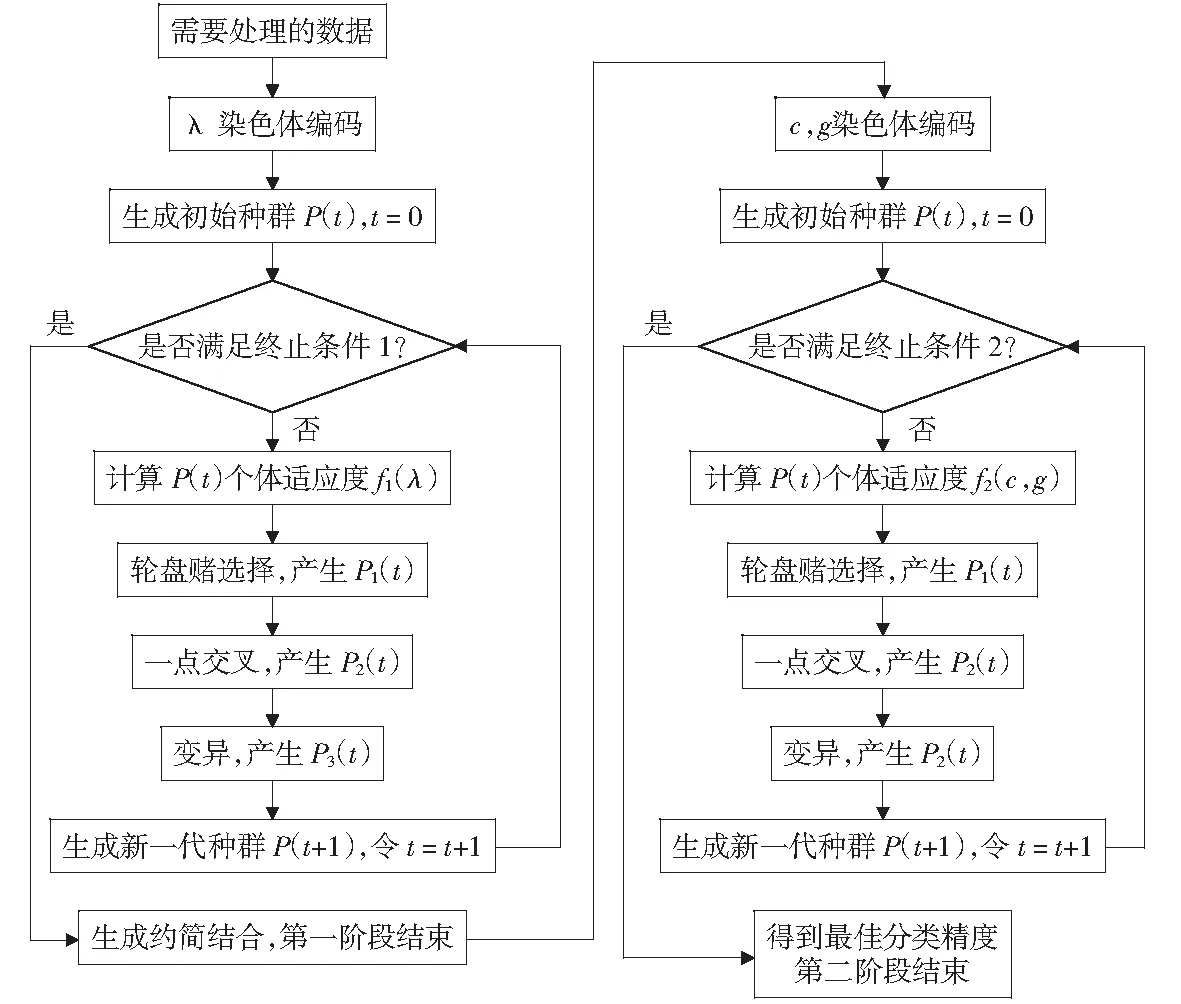
图1 算法流程图Fig.1 Algorithm flow chart

表1 算法参数设置Table 1 Algorithm parameter setling

(7)

式中：l为约简集合长度；T为所有条件属性个数；γB(λ)为邻域近似质量。为了防止在某些λ取值下约简集合个数过少致使核属性被约简，导致数据的分类性能严重下降，所以，通过(l(λ)-T/3)来保证最终约简集合长度不少于总长度的1/3，若小于1/3则适应度为负数，直接淘汰。这在一定程度上防止了核属性被约简的情况，且为了减少其对最终适应度大小的影响，将其比上本身的绝对值使其大小归为±1；(1-l(λ)/T)来保证约简集合长度越小越好的原则；μ为邻域近似质量与约简集合长度的可信度参数；同时为了使遗传算法收敛更快，采用指数函数。

由式(7)可以看出可信度参数μ的取值决定了适应度函数对约简集合长度或邻域近似质量的侧重度，所以可信度参数取值直接影响最终约简结果。对于可信度参数μ，取[0,1]之间以0.1为步长的10组数字，采用多晶硅G6和G7产品配料数据，比较不同μ下的邻域近似质量和约简集合长度来衡量可信度取值。实验结果如下图所示：

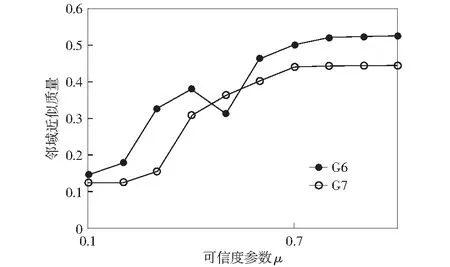
图2 两类多晶硅产品在不同μ下的邻域近似质量比较Fig.2 Field approximation mass comparison of two polysilicon products under diflerent reliability parameters

图3 两种多晶硅产品在不同μ下的约简集合长度比较Fig.3 Comparison of approximately combined set lengths of two kinds of polysilicon products under different reliability parameters

由图2和图3可以看出当可信度为0.7时，G6和G7数据的邻域近似质量达到相对较大值且趋于稳定，且都可以保持相对较小的约简集合长度4.同时考虑实际需求，对于工业数据的属性约简，约简结果的可靠性往往更加值得关注，所以本文的可信度取0.7.

2.1.2第二阶段适应度函数

将第一阶段输出的约简集合作为第二阶段的输入。第二阶段的目的是通过寻找最佳的惩罚因子c及核函数参数g来训练出准确率较高的分类模型。所以将第二阶段的适应度函数设置为测试集的预测精度(accuracy)，且为了综合评价NRS-SVM-GA模型，将第一阶段得到的约简集合长度(l)的适应值也写入适应度函数中，并设置其权重各占0.5，第二阶段适应度函数为：

(8)

同时本文采取k-折交叉验证(KCV)，首先将原始数据随机地分成k个互不相交的子集，每个子集的大小大致相等。用其中的一个子集作为测试集，其余子集的合集作为训练集，共进行k次训练和测试，每次选择不同的测试集，这样会得到k个模型，并用k个模型最终测试结果评价指标的平均数作为此KCV下的性能指标[11]。此外，在分类训练时对特征类别做标签化处理，按照工厂标准认为少子寿命值大于5.8 ms为合格类，小于5.8 ms为不合格类。

2.2 算法终止条件

由于算法两个阶段的目标不同，所以设置的终止条件也不同。

第一阶段的目标是得到较短的约简集合和较大的邻域近似质量，所以终止条件设为：当邻域近似质量大于某个峰值且约简集合长度为当前种群中的最小值时算法终止，根据大量多晶硅实际数据实验，这里将邻域近似质量峰值设为0.8；但在传代过程中可能出现无法满足上述终止条件的情况，所以如果满足连续传代个体最佳适应度保持N次不变或达到最大传代次数时算法也终止，考虑到算法的效率，将N设为5.

第二阶段的目的是训练出较好的分类模型，即较高的分类精度。所以直接将终止条件设为：当连续传代个体最佳适应度N次不变或达到最大传代次数时算法终止，同样考虑算法效率将N设为5.

3 实验分析

针对多晶硅铸锭生产的配料数据集，分别从运行时间和最终适应度两方面来对比标准遗传算法与两阶段遗传算法。

3.1 实验数据

本实验采用中电科2019年下半年多晶硅铸锭生产配料数据，其中包含G6和G7两种产品，每种产品包含8个配料类别，分别为免洗原生多晶块料、非免洗原生多晶块料、碎多晶铺底、碎片、中料、循环料、提纯锭芯(自产)、提纯锭芯(外购)，属性值为配料质量，最终评价指标为少子寿命值，属性值为其寿命值。其中G6产品有500个样本，G7产品有520个样本。G6与G7产品由于生产工艺及原料质量存在差异，导致少子寿命值评价标准不同，G6产品为少子寿命值大于5.8合格，G7产品为少子寿命值大于6.2合格。表2为G6产品的部分数据示例。

表2 G6多晶硅生产配料部分数据Table 2 Some date of polysilicon G6 production ingredients part of data

3.2 标准遗传算法参数设置

为了确保实验具有可比性，标准遗传算法参数与表1设置相同，由于标准遗传算法要同时满足得到较短约简集合和较高的分类精度，所以适应度函数设为两阶段遗传算法的第二阶段适应度函数:

(9)

终止条件与两阶段遗传算法第二阶段终止条件相同。

3.3 结果分析

由于多晶硅铸锭生产的配料数据集中在G6和G7两种产品上，因此本文分别使用标准遗传算法和两阶段遗传算法进行约简和分类，每种算法都进行20次实验，运行时间和适应度取其均值。两种算法的运行时间如图4所示，适应度如表3所示。

由图4可以看出，两阶段遗传算法在运行时间上远少于标准遗传算法，这是由于标准遗传算法要同时进行约简和分类两项操作，每产生一个约简集合都要进行一次分类训练，通过分类的结果来评价约简性能，这样极大地增加了算法的运算量。假设约简要进行n次循环，对每个约简结果的分类训练要进行m次循环，那么标准遗传算法的时间复杂度为T(n)=n+mn=O(mn)，而两阶段遗传算法将约简和分类操作单独进行，第一阶段属性约简的适应度函数不包含第二阶段的分类结果，所以极大减少了运算量，时间复杂度为T(n)=n+m=O(n+m).

图4 两种算法运行时间对比Fig.4 Comparison of the running time of the two algorithms

由表3可以看出，标准遗传算法的约简结果会出现核属性被约简掉的情况，导致分类精度直线下降，但适应度仍然较高，如产品G6的约简集合长度为2，但分类精度降低到73.22%.这是由于标准遗传算法的适应度函数是为了得到较少的约简集合个数和较高的分类精度，但忽略了某些邻域半径参数λ值下，为了达到约简个数越小适应度越高的目的，会使核属性也被约简掉，导致数据的分类精度大幅度下降，但由于约简集合个数较少，适应度仍然会保持较高的状态。而两阶段遗传算法在第一阶段给出了在约简个数不能少于总个数1/3的前提下，约简个数越少越好的原则，在一定程度上防止了数据核属性被约简掉的情况，且保证了数据整体较高的邻域近似质量，使边界域变小，从而降低数据的不确定性，同时也保证了数据的可分性。

表3 标准遗传算法与两阶段遗传算法适应度对比Table 3 Comparison of fitness between standard genetic algrithm and two-stage genetic algrithm

对比表3中两种算法可以看出，两阶段遗传算法中G6配料数据集中有12次适应度基本保持在0.704 4左右，G7数据有15次适应度基本保持在0.702 1左右；而标准遗传算法G6数据集中有17次出现核数性被约简掉的情况，G7数据集有18次核数性被约简掉的情况。由此可见，两阶段遗传算法的稳定性远高于标准遗传算法。

取两阶段遗传算法中适应度最高的G6和G7运行结果作为最终的多晶硅铸锭配料约简和分类结果，图5以柱状图形式表示出G6产品与G7产品的配料对少子寿命值影响所占权重。

由图5可见，G6产品中提纯锭芯(外购)对少子寿命值影响最大，而G7产品中提纯锭芯(自产)对少子寿命值影响最大；碎片、中料和循环料对G6和G7产品的少子寿命值均有一定影响且影响程度基本相同；免洗原生料、非免洗原生料和碎多晶对G6和G7产品的少子寿命值均无影响，该结果与实际专家给定值相符。

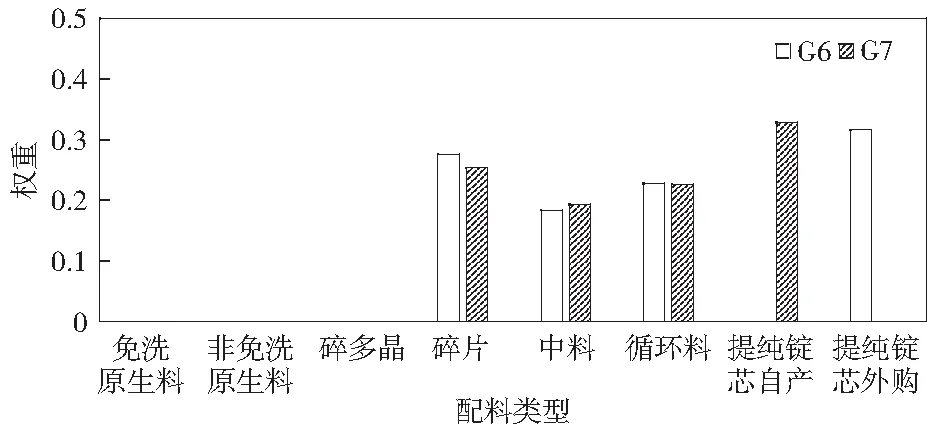
图5 G6和G7产品配料对少子寿命值影响所占权重Fig.5 The weight of G6 and G7 product ingredients on minority carrier lifetime

对于G6产品的属性约简结果为碎片、中料、循环料和提纯锭芯外购，并对其进行SVM预测，预测准确率可达到90.88%；G7产品的属性约简结果为碎片、中料、循环料、提纯锭芯(自产)，SVM的预测准确率可达90.43%，对实际多晶硅生产有一定的指导意义。

4 结论

传统的邻域粗糙集邻域半径取值采用经验值或者多次实验的方法来获得，往往不能快速有效地获取邻域半径，大大限制了邻域粗糙集在实际生产中的应用。本文采用遗传算法优化NRS-SVM模型参数，并将遗传算法分为两阶段进行，第一阶段提出通过代数观下的邻域近似质量及约简集合长度来综合评价约简性能，避免了以往通过分类器来评价约简性能所带来的时间消耗；将第一阶段约简结果直接作为第二阶段SVM分类器的输入，将其与标准遗传算法对比，实验结果表明，该算法在多晶硅铸锭配料数据集中平均运行时间在5～7 min，相比标准遗传算法平均减少了70 min，极大减少了工业数据分析中的时间消耗，且输出结果稳定，实现了NRS-SVM自动化特征提取及分类预测，为工业生产提供重要参考价值。