模块化软体机器人多模式运动分析
2021-05-21方占萍
方占萍
(酒泉职业技术学院,甘肃 酒泉 735000)
随着时代的发展,科学技术日新月异。在技术的支持下,软体机器人孕育而生。制作软体机器人材料有很多,如SMA[1]、硅胶等。运用这些材料可通过柔性方法让机器人改变尺寸结构。与传统机器人相比,这种机器人更加智能,不仅能实现人机交互,还能在医疗等领域大展拳脚,因此具有广阔的应用前景[2]。国内外学者纷纷加入研究队伍,Ge 等人以蚯蚓为参照物设计出一款软体机器人,王旭设计出一款可以完成蠕动爬行的软体机器人。本设计之所以采取模块化处理,优势在于方便运动速度及模式。将多个相同模块拼接在一起,可实现丰富运动序列的目的。
1 模块化软体机器人
1.1 结构设计
软体模块主要由2 部分构成,一是2 条多气囊结构,二是由底层、中间层、顶层组成的底板。之所以要让多气囊结构处于对称状态,目的在于让软体机器人拥有做差速运动的能力。在底板中,上下2 层均使用硅胶材质,中间层做特殊处理,使其具有不可拉伸的作用,防止底板变形。单个软体模块的规格是长度110 mm、宽度82 mm。
要想气囊运动,需要辅以驱动器。图1 展示的是气囊驱动器截面情况,其中Sa等于 13 mm,Sb等于 2.5 mm,Sc等于1 mm,Si等于14 mm,其余均为3 mm。利用3D 技术将驱动器的模具打印出来,再通过浇铸,即可获得成品。为让驱动器与底板连接紧密,需要使用粘结剂。一般情况下,选用硅胶或硫化胶。
软体机器人的运动方式参照尺蠖,由6 个模块构成。这些模块之间并无结构差别,只是独立供气。正是由于这一特点,使得软体机器人拥有诸多主动件,使得可选择的驱动序列有很多,这为丰富运动模式提供了可能。
1.2 前进波传递
图2将机器人前进波传递过程完整呈现。图中字母代表不同含义,a代表初始状态,这时还没有运动。b代表尾部模块,此时波形开始传递。d代表头部模块,此时波形已传递至此。c代表传递过程中,此时波形由2点向3点传递。当传递1 个周期后,机器人的位置情况见e。在完成4 个周期后,位置情况见f,此时机器人前进了11.6 cm的距离。
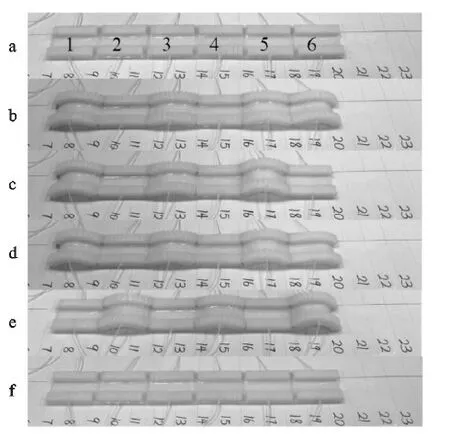
图2 A1D1模式的实验效果Fig.2 The experimental effect of A1D1 mode
2 多模式运动分析
2.1 单向前进运动
软体机器人要想具备单向前进的功能,需要满足2 个条件:一是在进行充气操作时,后方必须传递过来能量;二是在进行放气操作时,模块可将变形量向前方传递。
软体机器人的待放气模块位于左侧,待充气模块位于右侧。在待放气模块的左右各有一个变量,在待充气模块右侧也有一个变量。三变量之间的关系发生变化,运动情况也会随之改变[3]。
第1种情况,充放气模块运动。m代表一个模块的质量,μ代表摩擦因数,θ代表弯曲角度,far、fbl为静摩擦力。当模块两侧收到压力时测试结果表明,模块两侧的拉力值F和气压值p(t)、变形量Δl有着直接联系,其中当模块充气操作完毕后,此时变形量为ΔL。要想知道变形结果,关键要看运动前后的摩擦力值。已知a小于b,那么可以得出far<fbl。通过分析现有条件,可以看出模块后侧的摩擦力率先达到峰值,在力的作用下,模块后侧移动一段距离,此时模块模块中心点移动的距离ΔX等于至此,ΔX与a、b之间的关系就可梳理出来。
对于待充气模块M而言,ΔX与a、b之间存在如下关系:
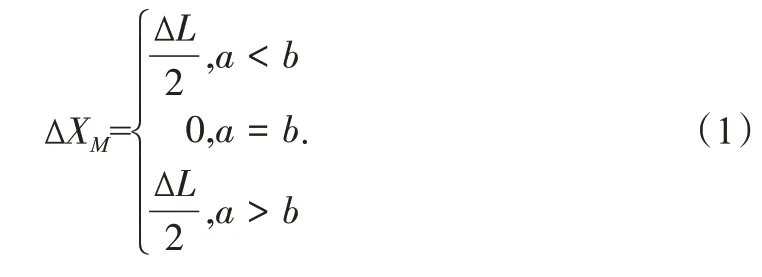
对于待放气模块N而言,ΔX与a、b之间存在如下关系:
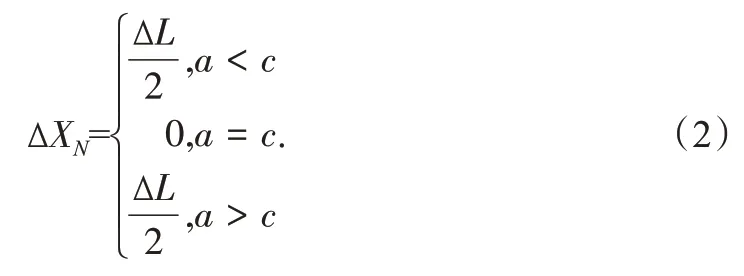
将2 个公式合并,可以得出:当a<b或a<c时,软体模块具备向前运动的能力。当a=b或a=c时,软体模块会把波形向前传递,但不会发生位移。
第 2 种情况,a等于b或a等于c。当a=c且a<b时,则有far小于fbl的结论,意味着此时模块左端的摩擦力处于峰值。
在完成一组传递后,如果模块N的中心点未发生变化,则能得出模块M右端不滑动的结论。此时模块M的变形量是在这个条件下,可以获得清楚最终拉力值模块N做完充气操作后,最终拉力值假设a等于c,那么FM与FN相等。
前文提到,与驱动力相关的因素只有2 个,一是气压,二是变形量。很显然模块M与模块N的变形量不一样,所以FM=FN的结论不成立,说明模块N的中心点会发生移动,并且是向右侧运动。因此,在a=c且a<b的条件下可达成运动传递的目标。同理可知,在a=b且a<c的条件下,模块运动量会向前传递。
综上所述,当满足a<b或a<c条件时,软体机器人可完成单向前进运动。
第3种情况,三者取值相同。假设一套操作完成后,模块N摩擦力的方向180°旋转,由向右变为向左,并且设定摩擦力向右作用距离为向左作用距离为Δx- Δz。经过测试观察可以看出,t放气<t充气。完成放气操作后,模块N会在力的作用下继续移动,此时移动距离为正。
无论做何种运动,都会遵循能量守恒定律,模块充放气过程亦是如此。当充气操作完成后,此时定义模块M的势能为EM(P,ΔLM),模块N的势能为EN(P,ΔLN)。在充气过程中,除了气体会做功,模块N的势能也会进行转化。这一过程可用下面公式表现。
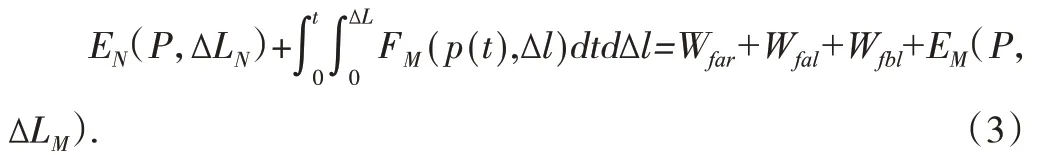
处于待放气状态的模块N,不同操作下能量变化方程有所不同。在充气时,方程是在 放 气 时 ,方 程 是EN(P,ΔLN)=
P(t)只和模块结构以及气压有关。当对模块M进行充气操作时,外摩擦力当对模块N进行充气操作时,外摩擦力已知a等于c,那么就可得到ΔLM等于ΔLN的结论。
综上可得:
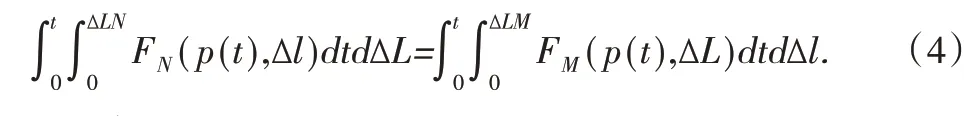
继而推导出:

将本节公式汇总到一起,就可获得这一方程:
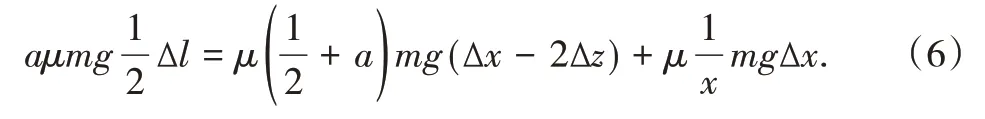
当a取值为 0 时,可以得出 Δx等于 Δz的结论,这与实验结果不符,说明在前进波传递中并不会形成新的能量。
当a取值为 1 时,结果是已知 0<Δz<可得出Δx的取值区间,即由此可以得出模块的中心位移范围,即
2.2 驱动序列分析
假设A代表模块处于充气状态,D代表模块处于待充气状态,i代表连续的充气模块,j代表连续的待充气模块,那么有AiDj代表不同类型的运动模式。充气模块相互组合即可形成前进波,再配以充气模块,就能组成一组驱动序列。a中拥有2 组驱动序列,模块1 与模块2 正进行充气操作,这种状态记作A2,模块3、模块4、模块5属于待充气状态,记作D3,模块6处于待放气状态,为下一组驱动序列的提供前进量[4]。
通过观察示意图,还可得出这样的数量关系。一般情况下,a等于i-1,b与c相等,均为j-1。倘若充放气模块紧挨边界,这时b或c不大于j-1。结合上一节内容来看,当j大于等于i时,软体机器人可实现单向前进运动。当二者取值相等时,a等于b等于 c 成立。在A1D1运动模式中,a值为 0,此时软体机器人无法前进。图8将这一模式下的运动效果整体呈现,由图可见,机器人在做完1 个周期运动后,基本没有挪动位置。在A2D2运动模式中,a值为1,此时机器人可完成单向前进运动。在A3D3运动模式中,a、b、c的取值不为2,必然会出现a值为2,b与c的取值为1 的情况,在这条件下无法实现单向前进运动。
综上所述,满足单向前进条件的运动模式有7种,分别是A1D2、A1D3、A1D4、A1D5、A2D2、A2D3、A2D4。只有在特定条件下,即i小于等于j,A1D6、A2D5、A2D6才能实现单向运动。
3 结语
本文对软体机器人进行模块化处理,内含多个驱动器,为驱动序列选择留有余地。通过一系列测试,获得模块之间的间隔关系,得到有效驱动序列。同时,联系前后文,准确判断出6 模块软体机器人可实现10 种运动模式。需注意的是,其中3种模式要在特殊条件下才能实现。
