基于改进MOPSO算法的区域侦察弹性星座重构方法
2021-05-21王浩张占月张海涛姜平
王浩,张占月,张海涛,姜平
1. 航天工程大学,北京 101400 2. 中国人民解放军63601部队,酒泉 732750
星座中部分卫星因故失效后重新调整星座构型的措施称为星座重构[1],按重构方式不同可分为在轨卫星重构和发射重构。在轨卫星重构是利用星座中现有卫星重新部署;发射重构是通过发射新的卫星提升受损星座性能。对区域侦察弹性星座的重构方法进行研究,可为侦察星座的建设提供参考。
文献[2-3]对在轨卫星重构方法进行了研究,提出了一种基于Lambert理论的星座重构方法,该方法采用Lambert转移对卫星进行轨道机动,对机动过程中的速度增量进行了优化。文献[4]对COMPASS导航星座的重构方法进行了研究,分别提出了利用低、中、高轨卫星和临近飞行器对失效星座进行重构的方法。文献[5]对以电推进方式进行轨道机动的星座重构方法进行了研究,运用组合算法解决了在星座重构过程中多星耦合机动的优化问题。文献[6]对全球导航星座的重构方法进行了研究,对受损星座中剩余卫星采用轨道机动的方式,通过遗传算法对调整卫星的选取及调整后卫星的相位进行了优化。文献[7]对区域覆盖星座的重构方案进行了研究,提出了保持轨道基本属性和星座构型的预置量轨道机动重构方法。文献[8]对导航星座的重构方法进行了研究,采取单颗邻位卫星机动、两颗邻位卫星机动和全部卫星机动的重构策略,考虑重构能量、重构时间、能量消耗均衡度、星座的可恢复性、性能提升程度,建立了星座重构优化模型。文献[9]对侦察星座的在轨重构方法进行了研究,考虑平均重访时间、最大覆盖时间,以及基于任务调度的覆盖总时长指标,建立了重构优化模型,并提出了一种变量维数可变的多目标差分进化算法,可有效求解重构过程中机动卫星和机动目标位置耦合优化问题。文献[10]提出发射新卫星和在轨卫星机动相结合的重构方法,通过发射卫星和在轨卫星机动形成一个新轨道面,对每颗卫星的位置及重构策略进行了优化,但并未考虑发射过程对重构的影响。文献[11]针对通信星座的重构方法进行了研究,采取在轨卫星相位重置的方式进行,以网络传输速率和延迟作为优化目标,建立了重构优化模型。
目前对星座重构方法的研究大多以在轨机动的方式对星座进行重构,该方法具有成本低、重构时间短的特点,在不考虑备份卫星机动的情况下只能减少星座性能下降程度,难以彻底恢复原有星座性能,而发射卫星重构的成本较高,重构时间与快速发射能力有关,将两者结合进行重构的方法研究较少。本文针对区域侦察星座重构问题进行研究,提出一种一箭多星发射和在轨卫星相位机动相结合的星座重构方法。首先对重构评估指标进行分析,提出弹性指数作为星座弹性的评估指标,其次对一箭多星发射过程和在轨卫星相位机动过程进行分析,建立基于重构时间和重构成本最优的重构优化模型。针对重构优化模型中的混合变量优化问题,对传统MOPSO算法进行改进,通过变量转化将离散优化变量转化为连续优化变量,提出基于学习机制的种群更新策略,并将改进的MOPSO算法应用于重构优化模型求解过程。
1 重构性能评估指标
覆盖指标众多,常用的覆盖指标有覆盖率、最大重访时间及空间分辨率,分别衡量星座对目标空间维、时间维和质量维的覆盖能力[12]。最大重访时间定义为目标区域内的点连续两次探测最大时间间隔的最大值,可通过网格点法计算[13]。本文选取最大重访时间作为侦察星座覆盖能力的度量指标。
重构成本按重构过程可分为发射的新卫星成本和在轨卫星机动成本,发射新卫星的成本由卫星载荷、总装集成测试、运行控制、地面支持设备以及发射成本构成,可利用小卫星成本估计模型(small satellite cost model, SSCM)计算单颗卫星的成本Csat[14]。卫星在轨机动成本可通过卫星机动所消耗的推进剂质量来衡量,对需机动的卫星进行编号,i为编号值,由火箭方程[15]可计算出卫星i所消耗的推进剂质量mi,如下式所示。
mi=m0(eΔvi/g0Isp-1)
(1)
式中:e为自然常数;m0为卫星质量;Δvi为卫星i机动所需速度增量;Isp=300 s为火箭发动机比冲;g0=9.8 m/s2为重力加速度。
假设在轨卫星机动消耗单位千克推进剂的成本为Cm,则可计算出重构总成本C。
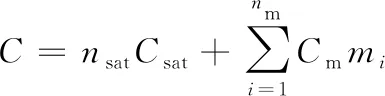
(2)
式中:nsat为新发射的卫星数量;nm为需进行轨道机动的卫星数量。
重构时间按重构过程可分为发射过程时间和在轨卫星机动时间。发射过程时间指新卫星通过一箭多星发射进入目标轨道所需要的时间,不考虑新卫星均匀部署到目标相位的时间。在轨机动时间指在轨卫星轨道机动到达目标位置所需时间。两个过程分步进行,先发射卫星形成新的轨道面,再对在轨剩余卫星机动,保证即使卫星发射失败,原星座构型保持不变,避免性能再度下降。重构总时间T可表示为:
T=tL+tphase
(3)
式中:tL为发射过程时间;tphase为在轨卫星机动时间。
弹性是衡量星座抗毁能力大小的指标,可通过星座受损后覆盖能力下降程度来衡量[14]。本文更关注于覆盖指标中最大重访时间的下降程度,将星座受损状态定义为星座中单颗卫星失效后最大重访时间下降幅度最大所对应的状态,定义弹性指数为星座从满站位状态到受损状态的最大重访时间下降幅度相对于满站位状态下最大重访时间的比例,弹性指数E如下式所示。
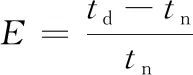
(4)
式中:tn为星座满站位状态下的最大重访时间;td为星座受损状态下的最大重访时间。
2 基于一箭多星发射和在轨卫星相位机动的星座重构方法
采用一箭多星发射和在轨卫星相位机动相结合的方式对星座进行重构,需要考虑两个方面,一是如何确定重构后星座的构型;二是在轨卫星如何通过相位机动到达目标位置。两者相互耦合,需要对问题解耦,首先对一箭多星发射过程和在轨卫星相位机动过程进行分析。
2.1 一箭多星发射过程分析
通过一箭多星快速发射形成新的轨道面是恢复星座性能的一种有效手段,发射任务流程如下:1)发射准备阶段:从发射任务下达开始到发射准备工作完成。2)发射等待阶段:发射准备工作完成后等待发射窗口的过程。3)发射阶段:从卫星发射到进入目标轨道的过程。4)调相入轨阶段:卫星在目标轨道上通过调相至目标轨道相位。
对发射过程分析之前,做如下假设:
1)采用机动发射方式。
2)为节省发射成本和入轨成本,采用共面发射方式,单共切入轨方式。
3)发射卫星型号、载荷与在轨卫星相同。
为保证星座构型的相对稳定,发射新轨道面的半长轴和倾角与原星座一致,轨面内卫星均匀分布。发射过程如图1所示,发射场经纬度(λ0,φ0),机动发射车速度为Vvehicle,机动发射区域为以发射场为圆心的球面圆形区域,其半径由机动发射车速度和发射准备时间决定,由几何关系可计算出机动发射区域的经度范围[λLmin,λLmax]和纬度范围[φLmin,φLmax]。机动发射点L的经纬度为(λL,φL),B点为L点天顶方向与目标轨道的相交点,C点为入轨点,发射新轨道面升交点赤经为Ωtar。以降轨发射为例,则从L点发射的等待时间tw为:
ϑ(t)-λL,2π)-tp
(5)
式中:mod 表示对两个数相除取余;Itar为发射新轨道面的倾角;ϑ(t)为初始时刻t的格林尼治恒星时角;w′为J2项摄动下目标轨道相对于地球的旋转角速度;tp为发射准备时间。
同理,采用升轨发射,发射等待时间tw为:
ϑ(t)-λL,2π)-tp
(6)
经过tw+tp时后,火箭从机动发射点L发射,经发射段飞行tf后到达入轨点C。已知发射地心角为αL,将火箭发射过程近似看做两冲量的开普勒轨道,则发射轨道上发射点L的真近点角fL=π-αL,发射轨道上入轨点C真近点角fC=π,根据轨道力学知识可得L点和C点满足下式[16]。
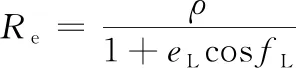
(7)
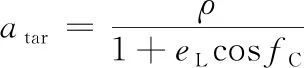
(8)
式中:Re为地球半长轴,取6 378.14 km;eL为发射轨道偏心率;ρ为发射轨道半通径;atar为目标轨道半长轴。
式(7)和式(8)联立解得ρ、eL,进一步求得发射轨道的半长轴aL:
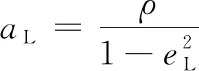
(9)
根据真近点角与平近点角的关系,可求得发射点L的平近点角μL,则可计算出发射段的飞行时间tf:

(10)
式中:μe为地球引力常数。
进入目标轨道后,新卫星按重构后的构型均匀部署于轨道面内。
2.2 在轨卫星相位机动过程分析
假设原星座各轨道面内卫星均匀分布,对存在失效卫星的轨道面内剩余正常卫星采取均匀相位的操作。如图2所示,该轨道面内卫星6、7、8失效,剩余正常卫星通过相位机动重新形成相位均匀的相对构型。已知存在失效卫星的轨道面数为I,按升交点赤经大小进行编号,i=1,2,…,I为编号值,轨道面内的卫星按纬度幅角大小进行编号,j为编号值。第i个轨道面内第1颗卫星的纬度幅角为Mi,1,则该轨道面内第j颗卫星的纬度幅角为Mi,j,如下式所示。
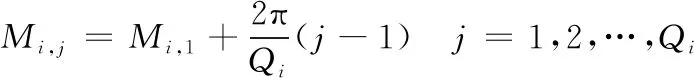
(11)
式中:Qi为第i个失效轨道面内原卫星总数。
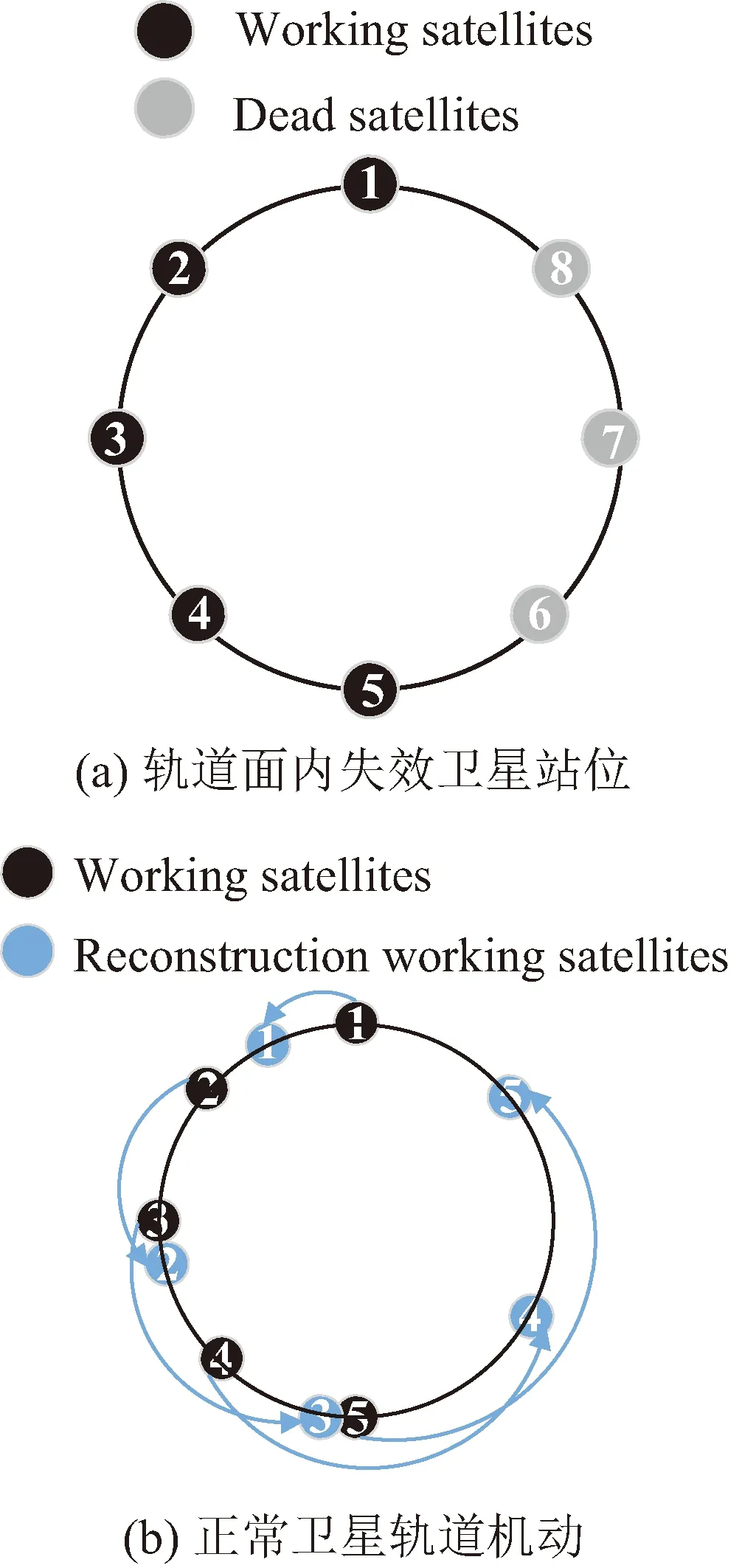
图2 在轨卫星均匀相位Fig.2 On-orbit satellites uniform phase
除去失效卫星后,重新按纬度幅角大小进行编号,k为编号值,则该轨道面上第k颗正常卫星的纬度幅角为Mi,k。
均匀相位可采用高轨调相和低轨调相方法进行。高轨调相过程如图3所示,卫星1从当前相位移动到目标位置,调相方式为卫星进入比目标轨道半长轴大的调相轨道,利用两个轨道的周期不同,逐渐减小卫星1和目标位置的相位差。具体实施方式为:卫星1首先沿速度方向加速进入调相轨道,在调相轨道运行一定圈数后到达目标位置时,再施加一个沿速度反方向的冲量进入目标轨道。低轨调相过程与此相反。当调相时间固定时,调相所需速度增量与卫星相位调整量成正比,当相位调相量ΔM∈(0,180]时,采用低轨调相所需速度增量更小,当ΔM∈(180,360)时,采用高轨调相所需速度增量更小。
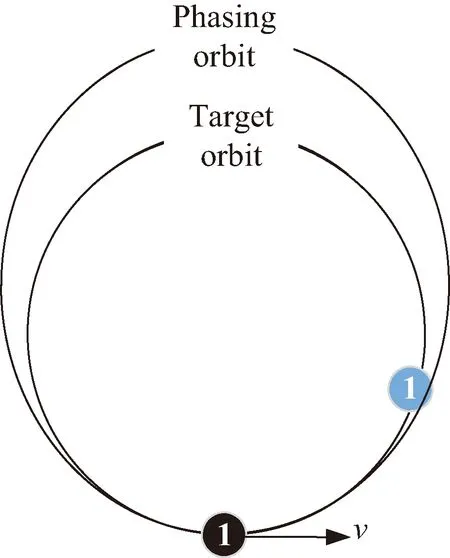
图3 高轨调相Fig.3 High orbit phase adjustment
均匀相位后第i个轨道面第1颗卫星的纬度幅角为Ki,1,则该轨道面第k颗卫星的纬度幅角为Ki,k,如下式所示。
k=1,2,…,Qi-Si
(12)
式中:Si为第i个轨道面内失效卫星数量。
第i个轨道面第k颗卫星相位调整量为ΔMi,k=Ki,k-Mi,k。当ΔMi,k∈(0,180]时,采用低轨调相,当ΔMi,k∈(180,360)时,采用高轨调相。
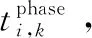
(13)
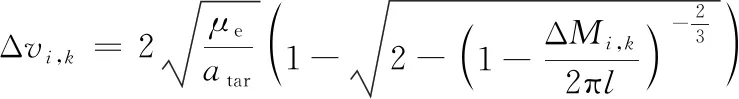
(14)
式中:Torbit为失效轨道周期。
若采用高轨调相,同理可得调相时间和调相所需速度。
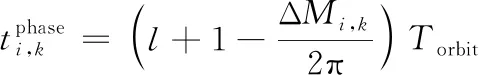
(15)
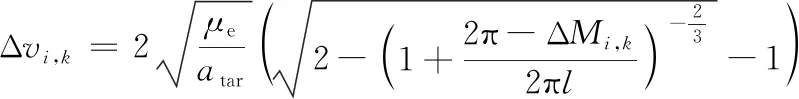
(16)
由式(1)和式(2)可计算出所有失效轨道面上正常卫星机动所需成本Cn为:
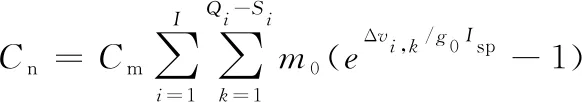
(17)
调相阶段所需总时间tphase为:
i=1,2,…,I;k=1,2,…,Qi-Si
(18)
2.3 基于重构时间最优的重构优化模型
以恢复原有星座性能为目的,要求重构时间最短,建立重构优化模型,该模型主要应用于应急状态下的重构任务。共存在5+I个优化变量:发射形成的新轨道面内卫星数S,机动发射点经度λL,发射点纬度φL,新轨道面的升交点赤经Ω以及轨道面内第1颗卫星的纬度幅角M0,第i个失效轨道面相位均匀后第1颗卫星的纬度幅角Ki,0(i=1,2,…,I)。
优化目标:
min (F,T,E)
(19)
式中:F为星座对目标区域的最大重访时间。
优化变量:
x=(S,λL,φL,Ω,M0,Ki,0)
(20)
约束条件:
1)为保证机动发射点能够发射目标轨道的卫星,机动发射点的纬度φL需满足:
φL≤itar
(21)
2)由于机动发射区域为球面圆区域,机动发射车速率为Vvehicle,发射准备时间为tp,机动发射点的经纬度除满足边界约束外,还需满足:
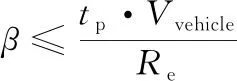
(22)
式中:β为机动发射点与发射场的地心夹角。
3)在轨卫星机动过程中,当ΔMi,k∈(0,180]时,优先选择低轨调相机动,调相轨道半长轴ai,k需高于低轨调相所允许的最小轨道半长轴。若不满足,则选择高轨调相。
ai,k≥Rx
(23)
式中:Rx为低轨调相所允许的最小轨道半长轴,一般取6 678 km;ai,k为第i个失效轨道面第k颗正常卫星的调相轨道半长轴。
2.4 基于重构成本最优的重构优化模型
重构目的为最小重构成本恢复原有星座性能,适用于常规场景下的重构任务,建立星座重构优化模型。模型中的优化变量、约束条件及优化步骤与基于时间最优的重构优化模型类似,不再叙述。
优化目标:
min(F,C,E)
(24)
添加约束条件:
1)发射过程优先选用降轨发射,当发射时机不满足降轨发射时,即降轨发射等待时间tw<0,表明无降轨发射时机,则选择升轨发射。
2)规定重构最大时长为Tmax,则重构总时间小于重构最大时长。
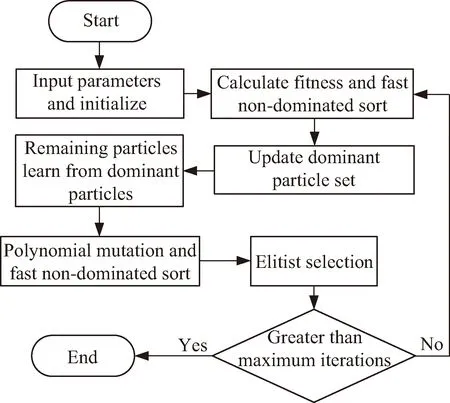
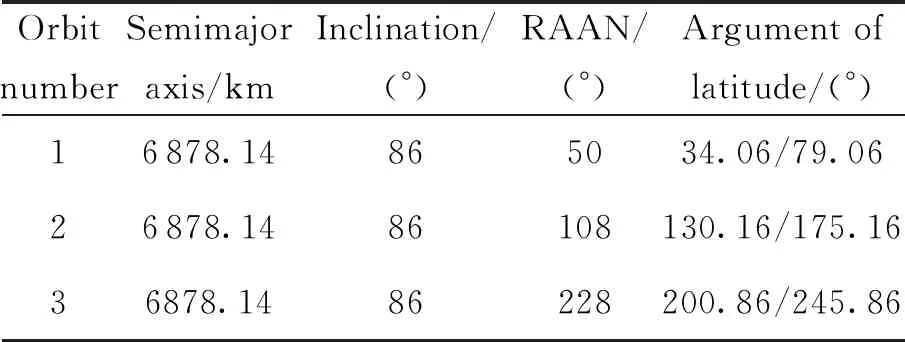
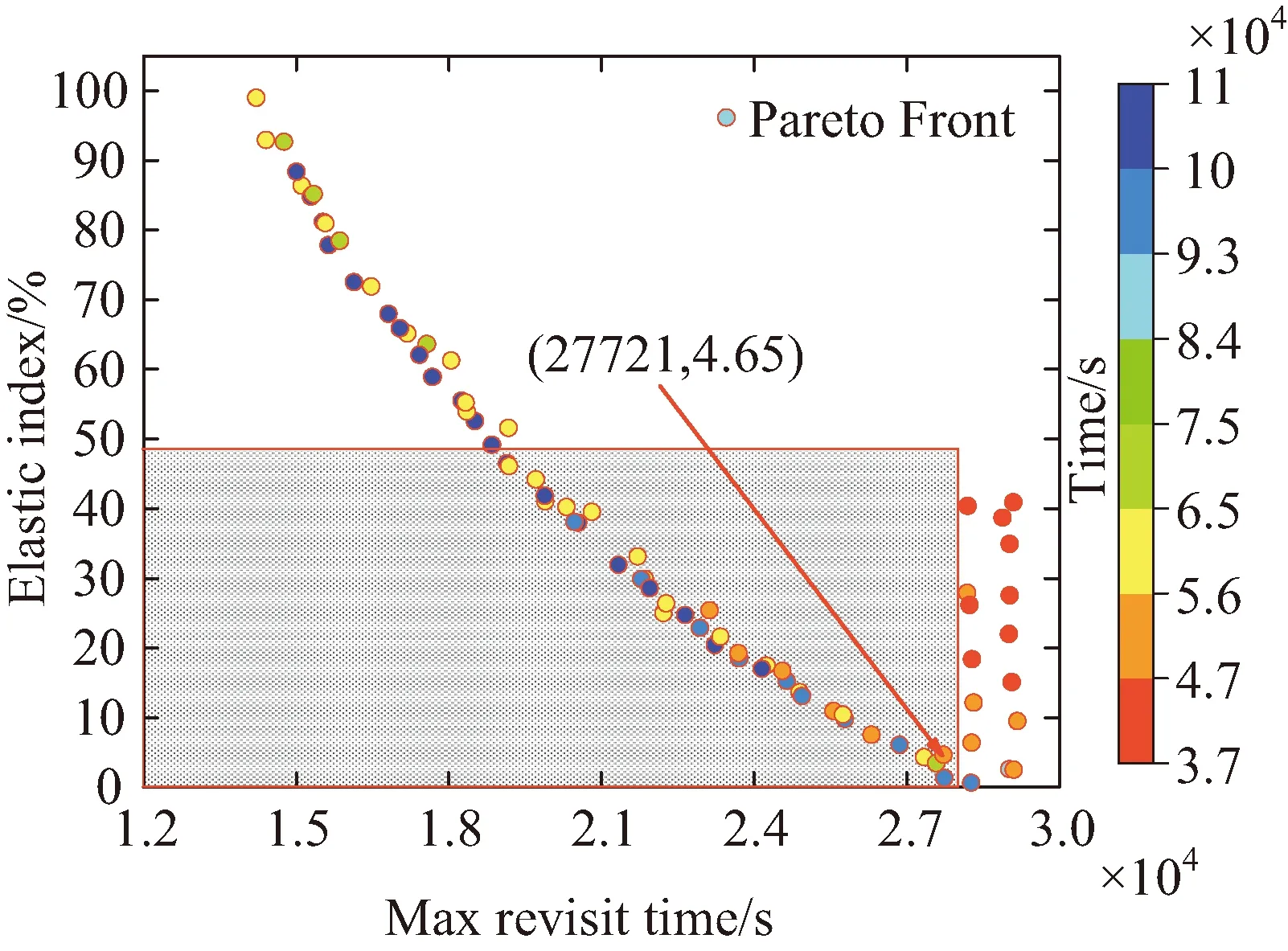
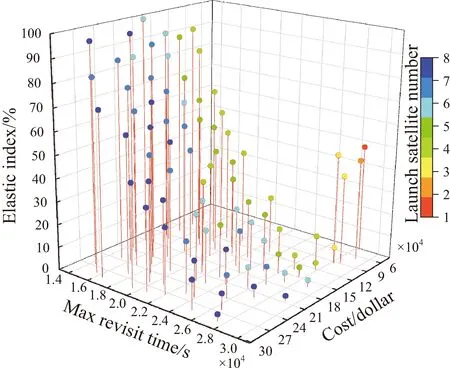
T (25) 传统的多目标算法对离散变量优化时多采取圆整和转化为约束条件的操作方法,而星座构型问题的离散变量一般为卫星数量和轨道面数,与轨道参数一同确定星座构型,共同影响星座的性能。若采取去圆整的方法将导致初期进化阶段卫星数量和轨道面数变化太快,无法对变量空间进行充分搜索,遗漏最优解。星座问题的强非线性导致约束条件越复杂越难得到最优解,将整数变量转化为约束条件加大了算法的收敛难度。针对这些问题,本文提出一种改进的MOPSO算法,首先通过变量转化法将离散变量转化为连续变量进行处理,其次利用约束支配关系将约束融入优化过程中,之后对种群进行Pereto支配排序,依据排序等级及拥挤度构建优势子种群集合,种群中其余粒子向优势粒子学习,算法流程如图4所示。 图4 MOPSO算法流程Fig.4 MOPSO algorithm flow chart 建立多目标优化模型,如下式所示。 min(f1(x),f2(x),…,fn(x)) (26) (27) 式中:f(x)为优化目标;x为优化变量;g(x)为不等式约束条件;h(x)为等式约束条件;n,m,p分别为编号值;M为不等式约束个数;P为等式约束个数。 优化算法常采用约束违反度cv来衡量解违反约束的程度,如下式所示,约束违反度越大,表明该解的适应度越差。 (28) 式中:ε为等式约束容忍值。 针对基于Pareto支配的多目标优化算法,通过约束支配关系可处理算法中目标与约束之间的关系。加入约束后支配关系如下[17],对于任意两个解xa、xb,当xaPareto支配xb时,需满足以下条件之一: 1)xa是可行解,xb是不可行解。 2)xa、xb都是不可行解,但cv(xa) 3)xa、xb都是可行解,xaPareto支配xb。 变量转换是一种利用映射关系将多种不同变量转换为同一类型变量的方法,从而有利于优化过程中对变量进行操作,常见的两种变量为离散变量和连续变量。将转化后的变量称为名义变量,连续变量的转化关系如下[18]: xr=a+bxk (29) 式中:xr为连续变量;a、b为实数;xk为名义变量,xk∈(0,1)。例如xr∈[2,7],则可通过名义变量表示为xr=2+5xk。 离散变量的转化关系如下[18]: xI=c+d·floor(xk) (30) 式中:xI为离散变量;c、d为整数。例如xI∈[1,5],则可通过名义变量表示为xI=1+floor(4xk)。 传统MOPSO算法需要建立外部档案,保存粒子的历史信息,操作复杂。本文提出基于学习机制的种群更新策略,只对当代粒子进行操作,增强了算法的收敛性。策略分为两步,第一步构建优势子种群。根据Pareto等级和拥挤距离选择优势粒子构建子种群方法如下:假设优势子种群的粒子个数为N1(N1 第二步对种群中其余N-N1粒子进行学习操作,粒子i学习过程如下:1)随机选择优势子种群中的一个优势粒子。2)粒子i向该优势粒子进行学习,使得种群逐渐靠近真实的最优解集。参考PSO算法中粒子速度和位置更新策略对种群进行更新,用该优势粒子替代历史最优粒子,用所有优势粒子的平均值代替全局最优粒子。速度更新公式为: (31) 位置更新公式为: xi+1=xi+vi+1 (32) 对更新后的种群粒子进行变异操作,以保证种群探索新粒子的能力,一般采用多项式变异。合并原种群和更新后的种群,进行精英选择,构成新种群参与下一代进化。 仿真时间为2021-01-01 00:00:00—2021-01-02 00:00:00,通过STK和MATLAB联合进行仿真。原星座参数:轨道高度为500 km,轨道倾角为86°,3个轨道面升交点赤经分别为50°、108°、228°,每个轨道内8颗卫星均匀分布,3个轨道面第1颗卫星的纬度幅角分别为34°、40°、20°。每个轨道面存在2颗失效卫星,轨道参数如表1所示。 表1 失效卫星轨道参数 经STK计算,可得星座满站位状态下对某一区域的最大重访时间为2.797 4×104s,弹性指数为0.48。在受损状态下,星座对区域的最大重访时间为3.97×104s,弹性指数为0.09。 设置初始参数如下:发射场经纬度值(100.5,41.1),机动发射车速度88 km/h,发射准备时间tp=2 h,则机动发射点经度值范围[98.4,102.5],纬度值范围[39.50,42.68]。卫星总质量m0=120 kg,在轨卫星机动消耗单位千克推进剂的成本Cm=200美元,火箭最大搭载量1 t,发射地心角αL=10°。在轨卫星机动阶段原失效卫星运行圈数l=5。 建立基于重构时间最优的重构优化模型,并通过改进的MOPSO算法求解,得到的Pareto解集如图5所示,图6为Pareto解集的最大重访时间与弹性指数的关系。 图5 Pareto解集(时间最优)Fig.5 Pareto solution set(time optimal) 图6 Pareto解集的最大重访时间与弹性指数的关系(时间最优)Fig.6 The maximum revisiting time and the elastic index of the pareto solution(time optimal) 如图6所示,阴影部分为重构后星座大于原有星座性能的重构方案,箭头所指的重构方案的重构时间最短,为51 711 s,为重构时间最优方案。具体发射方案为需要发射6颗卫星,机动发射点经纬度值为(100.53,40.68),发射的新轨道面升交点赤经为112.32°,面内第1颗卫星的纬度幅角为49.54°。在轨卫星相位机动方案为:均匀相位后3个失效轨道面内第1颗卫星的相位分别为32.75°、11.18°、29.03°。重构后星座对该区域的最大重访时间为2.772 2×104s,弹性指数为0.047,均优于原星座满站位状态下的指标值,满足重构要求。 以重构成本作为优化目标,建立基于重构成本最优的重构优化模型。规定最大重构时长为1天,得到的Pareto解集如图7所示,图8为Pareto解集的最大重访时间与弹性指数的关系。 图7 Pareto解集(成本最优)Fig.7 Pareto solution set(cost optimal) 图8 Pareto解集的最大重访时间与弹性指数的关系(成本最优)Fig.8 The maximum revisiting time and the elastic index of the pareto solution(cost optimal) 如图8所示,阴影部分为重构后星座大于原有星座性能的重构方案,箭头所指的重构方案重构成本最少,为1.09×105美元。具体发射方案为需发射4颗卫星,机动发射点经纬度值为(101.85,40.82),形成的新轨道面升交点赤经为177.46°,面内第1颗卫星的纬度幅角为154.57°。在轨卫星相位机动方案为:均匀相位后3个失效轨道面内第1颗卫星的相位分别为32.06°、49.57°、35.77°,重构后星座对区域的最大重访时间为2.723 6×104s,弹性指数为0.13,均优于原星座满站位状态下的指标值,满足重构要求。 本文对区域侦察弹性星座的重构问题进行了研究,提出了基于MOPSO的区域侦察弹性星座重构方法,并应用于某一受损星座的重构优化中。结果表明提出的方法及算法可有效解决重构时间最优和重构成本最优两类区域侦察弹性星座的重构问题。同时该方法也可拓展应用于通信、导航等星座的重构任务,只需将性能指标替换为通信、导航任务所关注的指标即可。本文仅分析了在轨卫星相位机动情况,除此机动方式之外,结合轨面间机动和发射考虑的重构方法可进一步进行研究。3 改进的MOPSO算法
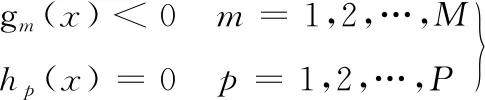
3.1 约束处理
3.2 变量转换
3.3 基于学习机制的种群更新策略

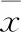
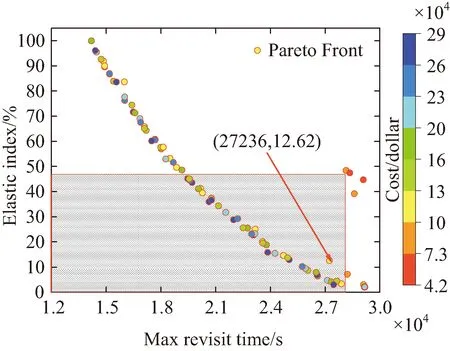
4 仿真校验

5 结束语
