航天器用低温多层隔热性能计算方程

张暘，赵剑锋，韩崇巍，张宁莉，宁博，杜卓林，赵欣，赵啟伟

1. 北京空间飞行器总体设计部, 北京 100094 2. 空间热控技术北京市重点实验室, 北京 100094

多层的一维纵向传热模型，普遍采用基于导热和辐射的形式[9-17]。传热模型分为两类,一类为半经验方程,另一类为逐层建模的方法。半经验方程以Lockheed[15-16]为代表，多层漏热量仅与多层内外表面温度有关，方程中的导热项系数和辐射项系数由试验确定。不同的结构、材料，导热项系数和辐射项系数有较大差异。并且，方程的辐射项为温度的4.67次方，不便于仿真软件使用。逐层建模的方法以McIntosh[17]为代表，需建立多层所有相邻反射屏间的传热方程。McIntosh给出了适用于间隔层为涤纶网、蚕丝网、玻璃纸的层间接触传热系数计算公式。此方法受多层结构、材料的限制较小，但是必须求解所有反射屏的温度，不便于工程应用。

本文将Lockheed和McIntosh的方法相结合，给出了适用于不同组成结构，并且便于工程应用的纵向传热模型获取方法。具体方法为：第一，按照McIntosh的方法逐层建立多层纵向传热模型，计算不同热边界情况下多层的传热量。第二，将多层传热模型简化为类似Lockheed方程的形式，辐射项改为温度的4次方，以适应仿真软件。利用第一步得到的计算数据，采用二元线性回归分析的方法，获得简化方程的导热项系数和辐射项系数。以国产低温多层为例，研究了常用10单元多层的隔热性能计算方程。通过等效方法及两个应用实例，验证了该方程的准确性。根据研究结果，指出了纯辐射模型以及纯导热模型的问题根源。

最后，研究了如何选取多层热平衡试验工况的问题。其难点是如何通过有限的试验工况获得足够的回归分析数据，即如何选择典型试验工况。经分析，确定了7个典型的试验工况，并给出了试验装置的选择建议。

本文的研究成果可以直接用于国产航天器低温多层的热设计、热仿真。考虑到低温多层的相似结构，本文提出的研究方法可用于其他类型低温多层。

1 一维纵向传热模型

1.1 热数学模型

航天器用低温多层包括两部分：多层芯和面膜。多层芯由反射屏和间隔层组成。反射屏为6 μm厚的双面镀铝聚酯打孔膜，间隔层为涤纶网。1层反射屏和1层涤纶网组成一个隔热单元。常用的隔热单元数为5单元、10单元、20单元。为便于多层制作，常增加1个反射屏，使多层芯的内外表面均为反射屏。面膜有两种：一种是黄膜，为25 μm厚带ITO膜的单面镀铝聚酰亚胺薄膜；另一种是黑膜，为25 μm厚黑色渗碳聚酰亚胺膜。图1为多层组成结构示意。

图1 多层结构组成Fig.1 Assembly structure of MLI

将多层纵向传热模型简化为仅有辐射和导热，忽略比重较小的层间分子导热(高真空)。按照图1可建立n单元多层相邻反射屏间的n个传热方程：

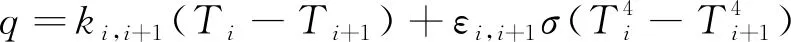
(1)

式中：i=1～n为反射屏编号；Ti为第i个反射屏的温度(K)；εi,i+1为反射屏间的等效发射率；σ为波尔兹曼常数；ki,i+1为层间接触传热系数(W·m-2·K-1)；q为多层传热量(W/m2)。面膜和第n+1层反射屏之间无间隔层，可认为二者是等温的。

反射屏间的等效发射率εi,i+1为：

εi,i+1=1/(1/εi+1/εi+1-1)

(2)

文献[17]给出了反射屏发射率εi随温度变化的计算式，考虑了反射屏打孔的影响：

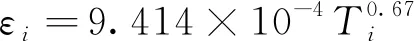
(3)

根据文献[15]可得间隔材料为涤纶网时层间接触传热系数ki,i+1的计算公式：

ki,i+1=0.008×f×k/ΔX

(4)

式中：f为涤纶网的相对密度(涤纶网面密度÷网厚度÷涤纶的体密度); ΔX为涤纶网的厚度。NASA某运载上面级低温储罐用多层[18]使用的涤纶网相对密度f=0.03。实测国产涤纶网面密度为10.615 g/m2，涤纶网厚115 μm，查材料手册涤纶的密度为1.39×106kg/m3。得国产涤纶网相对密度f=0.0664。k为涤纶材料的导热率，

k=0.017+7×10-6(800-Tm)+0.022 8ln(Tm)

(5)

式中：Tm为相邻反射屏的算术平均温度。

按式(1)可得n个方程，未知数为q，T1～Tn+1共n+2个，对任意给定的(T1、Tn+1)组合方程组均可解。

1.2 隔热性能计算方程

为了便于工程应用，期望隔热性能计算方程具有以下特性：第一，形式为导热项加辐射项(温度的4次方)；第二，变量仅包括传热量、多层冷/热面的温度；第三，等效导热项系数keff、等效辐射项系数εeff均为常数。

(6)

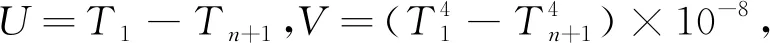
二元线性回归方程q=f(U,V)描述的是空间的一个平面，平面区域的轮廓由自变量U、V的取值范围确定。样本到平面的距离，代表回归方程的偏差，偏差越小回归方程的效果就越好。

线性回归的效果与样本密切相关[18-19]，一般要求样本容量大于30，并且在求解区域内均布。应用于低温多层的情况：首先，确定U、V的取值范围、确定求解区域；其次，在求解区域内均布样本。U、V的取值范围需要由T1、Tn+1转换。根据低温多层的耐温能力及应用经验，可以确定冷热面温度范围。T1为多层热面温度，取值范围为150～390 K(-123～117 ℃)；Tn+1为多层冷面温度，取值范围为90～390 K(-183～117 ℃)，由T1、Tn+1组成的求解区域如图2(a)所示。图2(a)中，ΔABE的区域与梯形ABCD内的区域关于直线AB对称，因此仅需考虑梯形ABCD区域。梯形ABCD区域映射为图2(b)所示的纺锤形区域B′C′D′A′(B′)。在图2(b)中均布35个样本，不含坐标原点。35个样本在原坐标系下的分布如图2(a)所示。

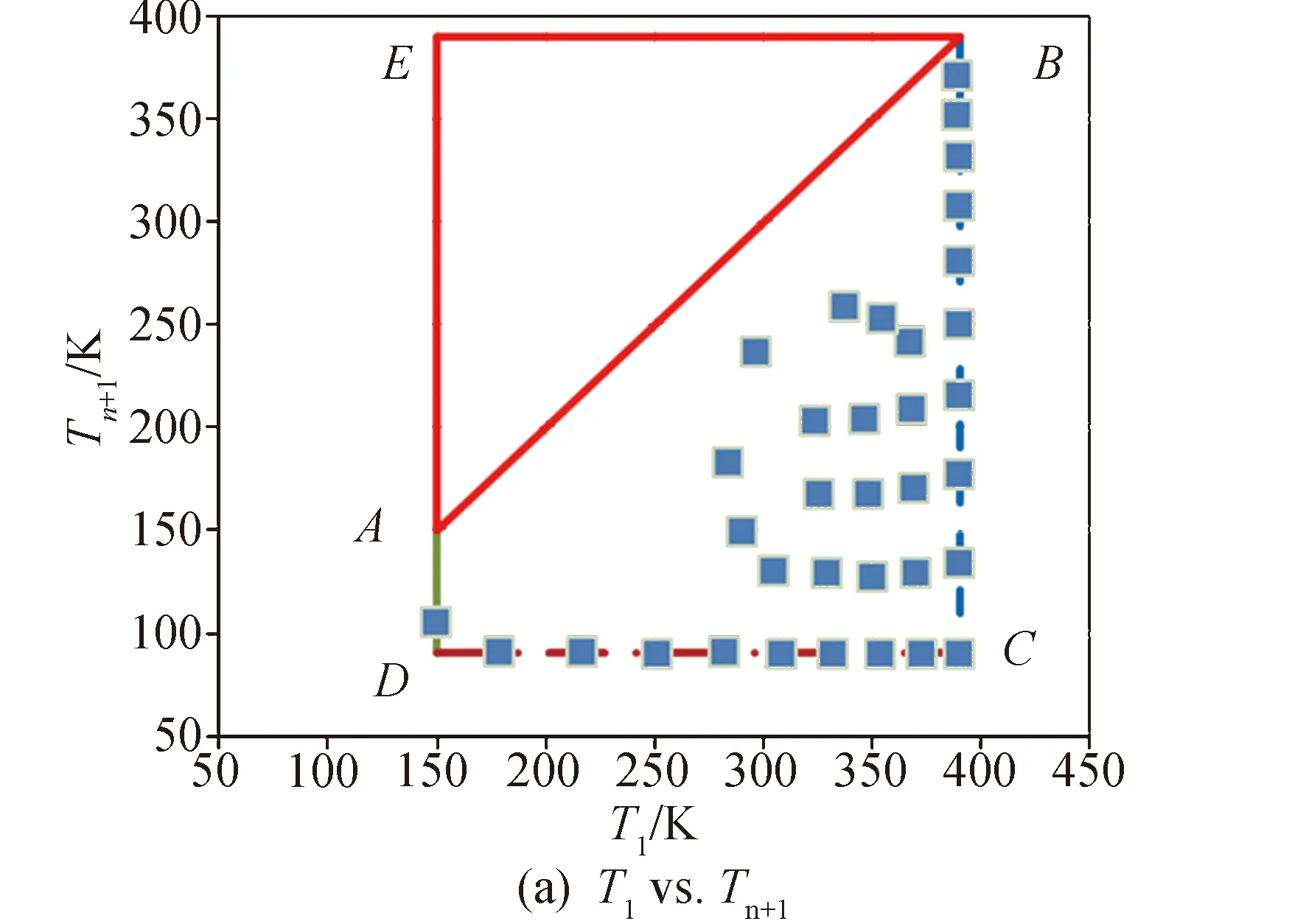
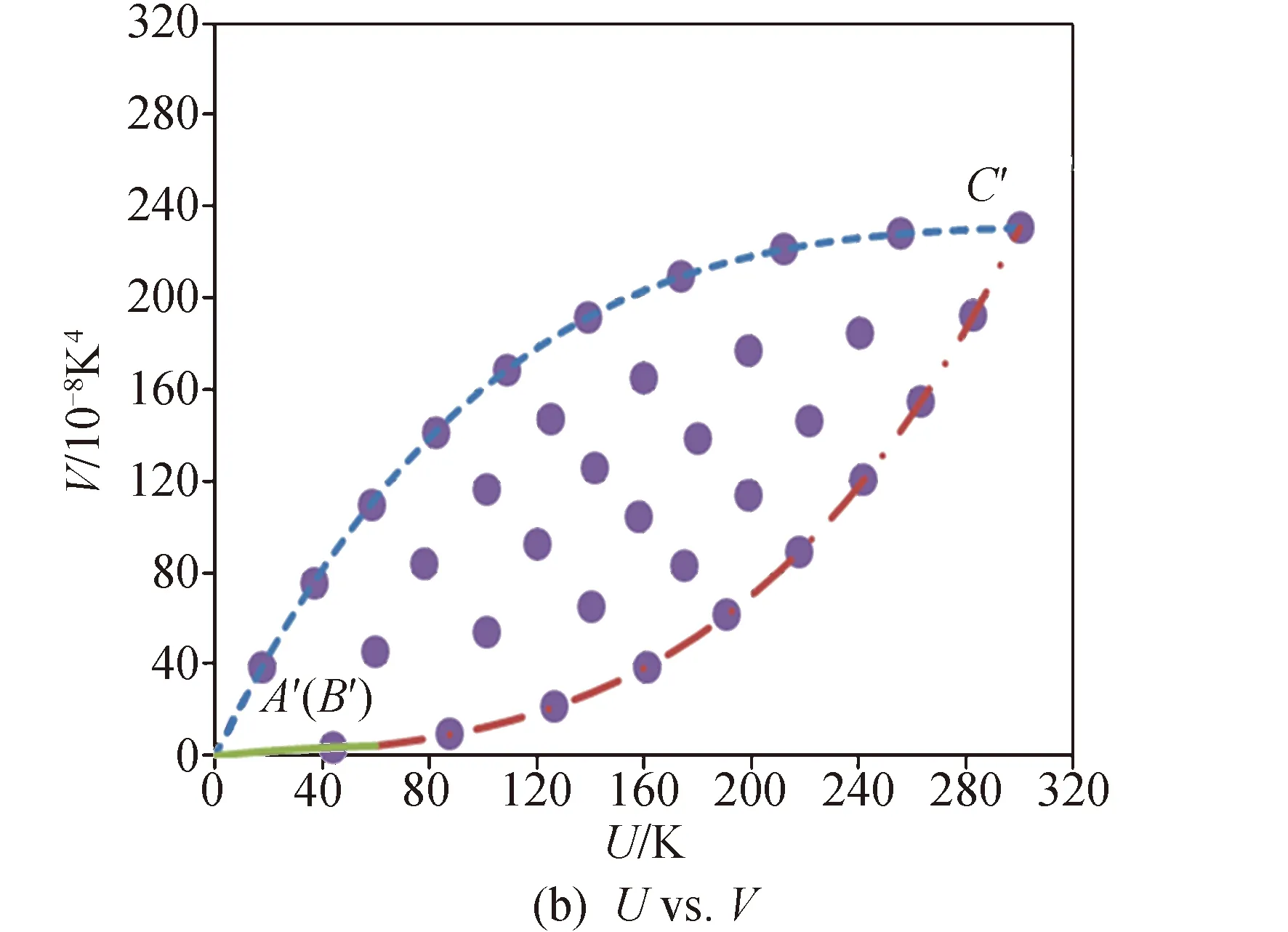
图2 求解区域及样本分布Fig. 2 Solution region and sample distribution

线性回归的效果还需通过回归方程的显著性检验及回归系数的显著性检验[18-19]。检验项目以及判据见表1。R2检验用于衡量回归方程的优劣性，即拟合程度如何。F检验用于检验因变量与自变量是否存在显著的线性相关关系。t检验用于检验每个自变量的系数是否显著为零，即方程中是否有多余的自变量。表中，k为自变量个数，n为样本容量。

表1 显著性检验项目

综上所述，获得隔热性能计算方程一般分4步。第一，确定样本的自变量取值。根据图2确定(T1、Tn+1)的35种组合。第二，获得样本的因变量值。对每一对自变量，求解按第1.1小节建立的方程组，获得35个因变量值(q)，从而获得35个观测样本(q，T1，Tn+1)。第三，利用观测样本，按式(6)进行线性回归，获得常数项系数。第四，按表1进行显著性检验。

2 算例

以10单元低温多层为例。按第1.2小节的方法获得了两组观测样本，分别对应f=0.064、f=0.03，如表2所示。从表2可知，f值对多层的漏热量q影响较大，国产多层应采用相对密度更小的涤纶网以提高隔热性能。将两组样本绘制成三维散点图，并将散点拟合成三维曲面，如图3所示。可见散点拟合的曲面均为平面，直观判断式(6)的形式是正确的。

利用专业软件做回归分析，回归方程的形式为：

q=b0+b1U+b2V

(7)

得b0=-0.007 8，b1=0.061 4，b2=0.02/5.67。b0很小，对漏热量影响可忽略，令b0=0。对照式(6)，得keff=0.061 4，εeff=0.02/5.67。最终，将隔热性能计算方程写为：

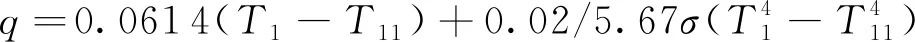
(8)

显著性检验结果为：R2=0.999 9接近于1；F检验为1.75×105>F0.05(2,32)=5.34。回归系数的显著性检验结果为：b1的t值为482.4，b2的t值为135.3，均大于t0.05(32)=2.04。可见，回归方程的效果是很好的。此外，按式(8)计算的漏热量与样本q值最大偏差为2.4%，平均偏差为0.8%，方程的精度较高。

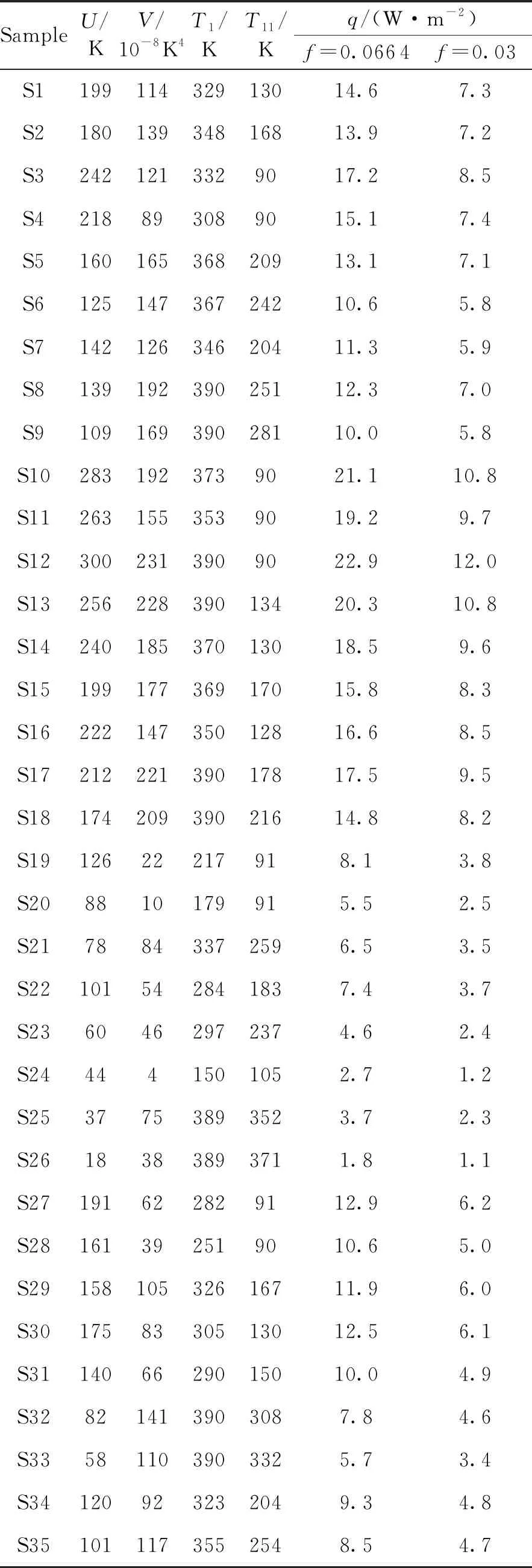
表2 10单元多层样本

图3 样本三维曲面Fig. 3 Sample 3D surface

3 验证计算方程

3.1 常用温度条件等效验证

为了避免有限次试验数据带来的误差，并且省去大量、繁杂的试验数据处理工作。先采用等效的验证方法，验证常用温度条件。再进行典型低温、高温工况的验证。

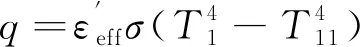
(9)

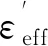
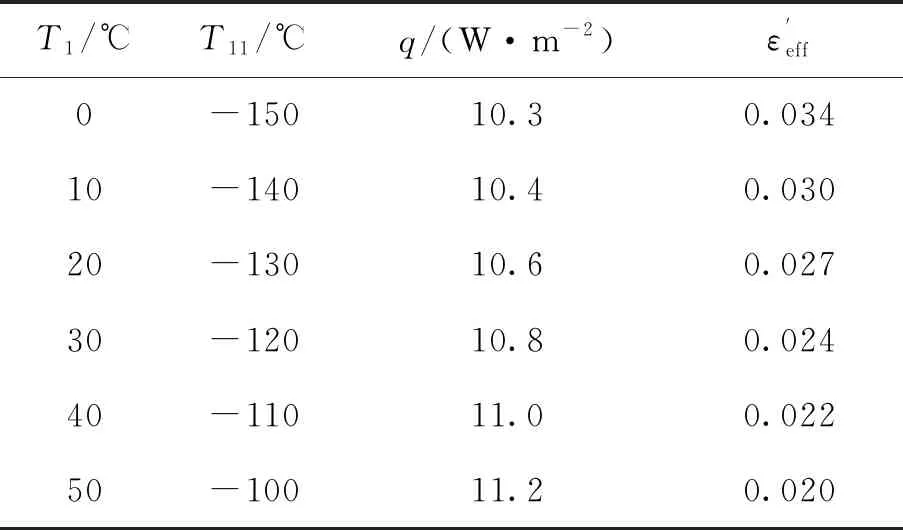
表3 10单元多层等效验证

3.2 典型高温、低温工况验证

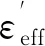
表4 地面试验仿真结果

图4 在轨仿真结果Fig. 4 Inorbit simulation result

4 有效发射率取经验值的问题根源

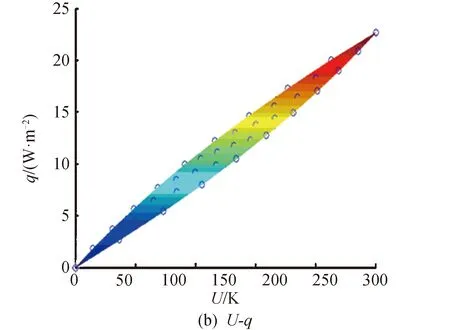
图5 平面投影Fig. 5 Plane projection

5 试验工况设计

本文只研究试验工况设计相关的问题，包括两方面：如何选取试验样本，即试验工况如何确定；以及如何实现试验工况，即采用什么试验装置完成试验。

多层热平衡试验时间很长，真空罐、液氮等试验费用昂贵。若按第1.2小节取35个样本，很难实现，因此需要研究最小样本容量。按文献[20]，可得样本容量的下限要求。第一，欲使回归参数存在，样本容量(n)至少比模型自变量个数(k)多1，即n≥k+1；第二，t检验对样本最小容量要求为n>k+5；第三，为了提高估计精度，要求n>2k。因此，对二元线性回归，样本容量至少为7个，不含坐标原点。按照样本均布的原则，布置7个样本，如图6中S1～S7。样本的坐标及其对应的多层冷热面温度见表5。

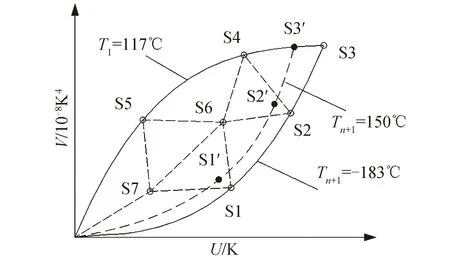
图6 试验样本分布Fig. 6 Thermal balance test sample distribution

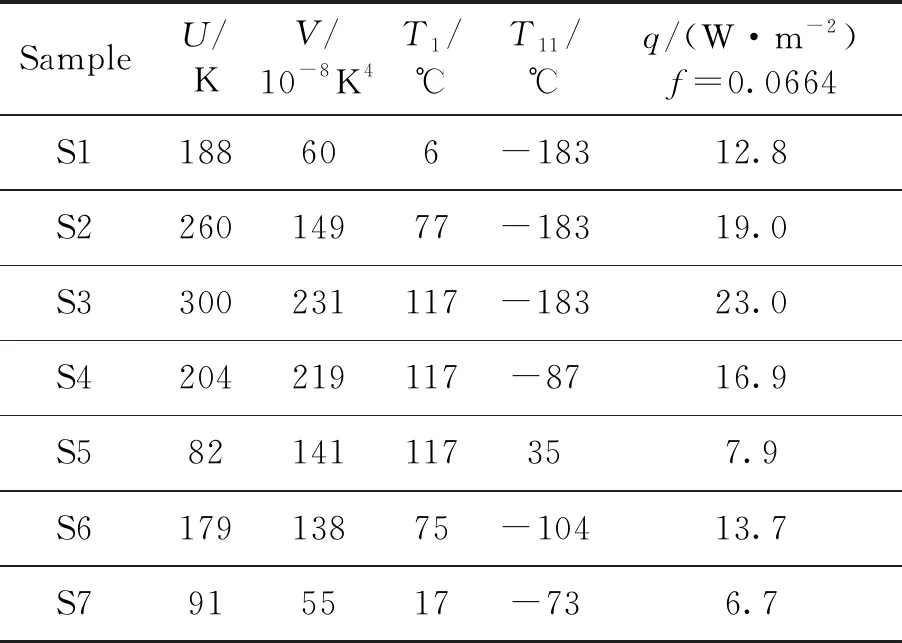
表5 热平衡试验样本

要实现表5的试验样本，多层冷、热面都必须控温。多层热面控温比较容易实现，控制热面加热器功率即可。多层冷面温度控制要复杂得多，与试验装置有关。根据冷面不同的控温原理，将试验装置分为三类[6,10]。第一类为汽化型，第二类为对流换热型，第三类为辐射换热型。

汽化型装置：多层的冷面紧贴一个容器，容器内填充低温工质(液氮、液氦等)，靠液态工质汽化维持冷面温度恒定，并根据汽化量计算多层漏热。这种试验装置精度高，一般用于多层冷面温度较低情况的性能测试。缺点是试验系统复杂,费用昂贵。

对流换热型装置也需要一个容器存放低温工质，但工质不汽化，靠工质与容器壁面对流换热控制冷面温度。这类设备适用于冷面温度不是很低的情况。测量精度不如汽化型，但冷面温度可连续控制，装置简单，费用不高。

辐射换热型装置更简单，仅需将试验件吊挂在真空罐内，多层冷面与真空罐壁直接辐射换热。根据经验，此方法所得的多层冷面温度受多层热面温度影响很小，冷面温度一般为-150℃左右，该方法对冷面的主动控温效果较差。

综上所述，针对表5的S1～S3样本，可采用汽化型装置，选液氮为汽化工质。为了节约试验经费也可以采用辐射换热型装置。此时冷面温度为-150℃左右，对应的样本变为S1′S2′S3′，稍偏离原样本。其余样本需采用对流换热型装置，实现多层冷面温度的主动控温。

6 结束语

本文以间隔层为涤纶网的国产10单元低温多层为例，研究了获取低温多层隔热性能方程的方法。此方法具有普遍适用性，可用于任何单元数、间隔层为玻璃纸或蚕丝网的情况。

与低温领域常用的Lockheed方法相比，本文给出的隔热性能计算方程可更方便地用于热仿真软件，并且有足够的计算精度。

本文描述的隔热性能计算方程针对一维纵向传热过程，适用于大面积应用的多层。若多层面积较小，还需考虑多层的横向漏热问题。