基于熵权-模糊层次分析法的战场通信网抗毁性指标研究*

宋玉龙，王 磊，武欣嵘，姚昌华，曾维军，宋天挺

（1.陆军工程大学，江苏 南京 210007；2.南京信息工程大学，江苏 南京 210044；3.东部战区陆军参谋部，福建 福州 350001）

0 引言

随着网络化科技的不断发展，现代战争对通信系统的依赖程度日益增大。通过指挥控制将作战单元、武器装备，以及单兵等联系起来形成整体作战能力，是掌握战争主动权的关键。战场通信网作为指挥控制的重要依托，受到恶劣环境、敌方攻击等影响，提高战场通信网维持其功能的能力对于打赢信息化战争具有重要的军事价值。网络抗毁性是评价战场通信网的一个重要性能指标。受到广泛认可的网络抗毁性定义为网络中的节点（边）故障或遭受摧毁失效后，网络能继续完成其任务的能力。在对战场通信网进行综合评估和建模优化时，都需要一个合适的测度衡量网络抗毁性，并以抗毁性测度为目标对网络进行分析研究。

网络抗毁性指标是近年来的研究热点，学者们从不同角度衡量网络抗毁性，取得了较多的学术成果。以建立生存性较高的网络为目的，采用点（边）连通度衡量网络抗毁性，即网络变为不连通需要失效的最少节点（边）数。以图论为基础，学者们提出了坚韧度、粘连度、完整度和离散数等抗毁性指标。但是随着网络规模增大应用存在局限。以复杂网络为背景，提出最大连通子图和平均最短距离等网络抗毁性指标。近年来，考虑网络冗余度、谱测度和自然连通度，以及加权自然连通度作为抗毁性指标优化网络拓扑受到广泛关注。此外还有聚类系数、网络效率、介数以及临界移除比等自定义抗毁性指标。针对战场通信网的抗毁性指标研究应用也取得了一定的进展。文献[1]针对防空反导指挥网络特点构建抗毁性评估指标体系，通过专家打分量化得到数据，利用BP 神经网络训练得到网络抗毁性评估模型。文献[2]利用基于图论的抗毁性指标对军事通信网进行建模，分析节点（边）重要度以及网络抗毁性。

对于抗毁性指标的研究已经取得了较多的成果，但是以单一指标衡量网络抗毁性研究为主，从多属性决策的角度考虑建立网络抗毁性综合评价指标研究较少。本文根据战场通信网的需求特点，针对网络拓扑构建抗毁性指标评价体系，提出基于熵权的模糊层次分析法，对指标赋权得到抗毁性综合评价指标，并对典型战场通信网进行分析验证，得到的加权抗毁性指标对战场通信网建模优化提供一定的理论建议和支撑。

1 战场通信网抗毁性指标

战场通信网是一个相对复杂的网络。在高技术条件下的现代战争中网络规模、战场信息成倍增长。研究表明，战场通信网表现为一个复杂网络的小世界，且无标度特征[3]。根据战场通信网网络连通性和网络效率要求高等特点，针对网络拓扑结构，主要分析以下6 种抗毁性指标，其中基于复杂网络抗毁性指标为自然连通度、网络效率、平均聚类系数和介数，以及基于图论的抗毁性指标为平均度数与极大连通子图。

（1）自然连通度。为基于特征谱的测度，其原理是节点间路径的冗余度，根据网络邻接矩阵的特征值得到，定义如下：

式中：N为网络中节点个数；λi为网络邻接矩阵的特征根，将网络的特征谱与网络抗毁性建立了联系。

（2）网络效率。网络中两节点之间存在最短路径，最短路径越短信息传递经过的跳数越少，网络效率越高，即网络效率与节点间最短路径的长度成反比，定义如下：

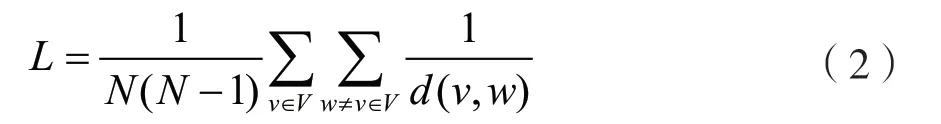
式中，N为网络节点个数，V是网络节点集合，v、w是网络中的节点，d(v,w)为两节点间的最短路径长度。

（3）平均聚类系数。聚类系数反映了节点附近网络的连通性，平均聚类系数是网络中全部节点聚类系数的平均值，用来衡量整个网络的连通性，定义如下：

式中，N是网络节点个数，Ei是节点i的近邻之间存在的连通边数目，k代表与i有连线的节点数目。

（4）平均介数。介数分为节点介数和边介数两类。节点介数是网络中最短路径通过某一节点的条数，平均节点介数是全部节点介数的平均值。平均节点介数定义如下：

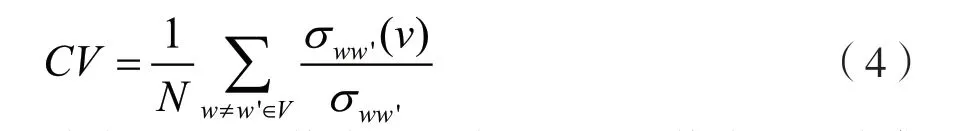
式中，v是网络中的节点，V是网络中的节点集合，σww'是节点w和w'之间的最短路径数，σww'(v)是节点w和w'之间所有最短路径经过节点v的条数。

边介数是网络中最短路径通过某条边的条数，平均边介数是全部边介数的平均值。平均边介数定义如下：

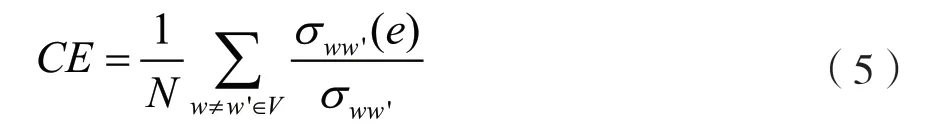
式中，e是网络中的边，V是网络中的节点集合，σww'是节点w和w'之间的最短路径数，σww'(e)是节点w和w'之间所有最短路径经过边e的条数。

（5）平均度数。节点度数是某一节点的所有连边数，平均节点度数是全部节点度数的平均值，定义如下：

式中，V是网络中的全部节点集合，N是网络中节点个数，当i,x之间有连接时aix=1，当i,x之间没有连接时aix=0。

（6）极大连通子图。图G的极大连通子图称为图G的连通分量，即图G最大连通分支中包含的节点数目。定义如下：

式中，G'是图G的连通分支，num(G')是连通分支的节点数。

2 熵权-模糊层次分析法

2.1 层次分析法

层次分析法[4]（Analysis Hierarchy Process，AHP）是将决策者对某一事物的主观评价进行量化的方法，是一种定性与定量相结合、层次化、系统化的分析方法，得到决策问题的定量结果。层次分析法主要有以下4 个步骤。

（1）建立层次结构模型。根据需要解决的问题、所要达到的目的构建层次结构模型如图1 所示。

图1 层次结构模型

指标层中每个因素都对目标产生影响，其中指标层可根据实际情况进一步细分，构建多层次模型。

（2）构造比较判断矩阵。按照成对比较结果构造比较判断矩阵A，表示本层所有因素对上一层某一因素的相对重要性的比较，即采用一定的标度对人的主观感觉进行量化，常用的标度方法有1-9、1/9-9/1、10/10-18/2 和指数标度法等。aij为要素i与要素j的比较结果。比较判断矩阵A表达式如下：

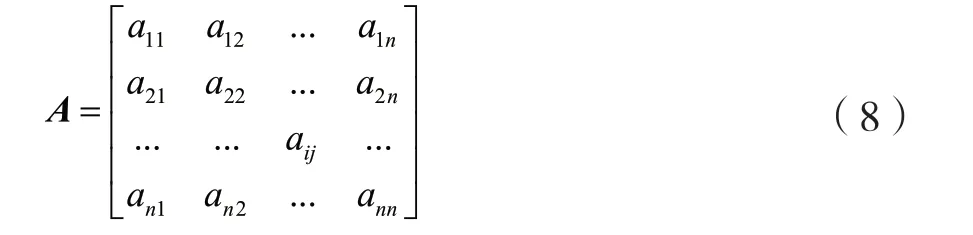
比较判断矩阵A是正互反矩阵，满足aij=1/aji＞0和aii=0。

（3）一致性检验并计算权向量。在使用比较判断矩阵A求权重前必须进行一致性检验，若正互反矩阵A满足aik=aij×ajk，则A为一致性矩阵。然而A往往是不一致的，所以要进行一致性检验。利用以下3 个步骤完成一致性检验。

①计算一致性指标CI，公式如下：

式中，λmax、n分别是矩阵A的最大特征值和阶数。

②根据表1 查找对应的平均随机一致性指标RI。

表1 平均随机一致性指标

③计算一致性比例CR，公式如下：

若CR＜0.1，则认为A的一致性可以接受；否则需要对A进行修正。

在比较判断矩阵A通过一致性检验后，可利用算术平均法、几何平均法以及特征值法计算权重量。

（4）计算组合权向量。组合权向量可作为决策者选择方案的依据。

2.2 模糊一致矩阵

针对层次分析法中比较判断矩阵存在的问题，采用模糊数学中的模糊一致矩阵[5]替换传统层次分析法的比较判断模型。

2.2.1 相关定义

若存在一个方阵Fn×n，第i行第j列元素为aij，则有：

（1）满足条件F=(aij)n×n,其中0 ≤aij≤1，则矩阵F是模糊矩阵；

（2）满足条件F=(aij)n×n,其中0 ≤aij≤1 且aij+aji=1，则矩阵F是模糊互补矩阵；

（3）满足第1 个条件且同时满足条件aij=aikakj+0.5,其中i,j,k∈{1,2,…,n}，则矩阵F是模糊一致矩阵。

2.2.2 模糊一致矩阵性质

模糊一致矩阵具备模糊性、对称性以及一致性，能较好地应用到传统层次分析法。

（1）模糊性。模糊一致矩阵中所有元素都在0到1 之间，传统层次分析法中需要对因素两两比较得到相对重要值，利用模糊性可以将重要值放缩到0 到1 之间，从模糊关系的角度得到因素之间的重要程度。

（2）对称性。矩阵对角线上的元素aii=0.5，表示因素与自身对比重要性相等。当矩阵元素aij＞0.5时，表示因素i比因素j重要。当矩阵元素aij＜0.5时，表示因素j比因素i重要。若aij=k表示因素i相对因素j重要程度，则aji=1-k表示因素j相对因素i重要程度，从线性角度给出了衡量因素重要性的数值。

（3）一致性。若aij表示因素i相对因素j重要程度，aik表示因素i相对因素k重要程度，akj表示因素k相对因素j重要程度。一致性满足以下两个定义：一是加性定义aij=aik-ajk+0.5；二是乘性定义aijajkaki=ajiakjaik。判断矩阵一致性的充要条件为矩阵任意行与其他行的差是一个常数。一致性符合逻辑定义且相较于传统层次分析法中一致性检验计算复杂度较低。

2.3 熵权法

熵权法[6]是一种客观赋权的方法，其原理是根据指标的变异程度大小，即所包含的信息量大小进行赋权。熵权法计算权重步骤如下：

（1）建立评价数据矩阵。假设有n个评价对象和m个评价指标，则评价数据矩阵为：

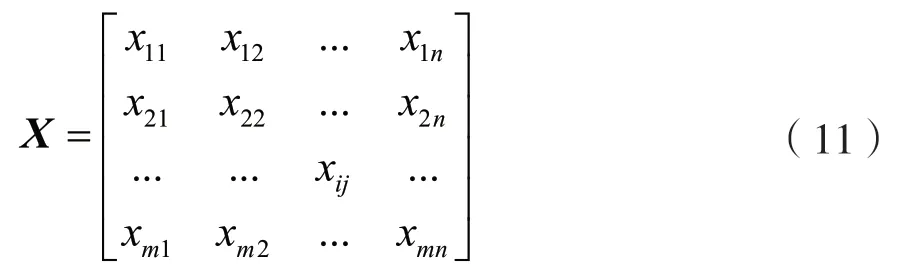
式中，xij为第j个指标下的第i个评价对象的值。

（2）利用式（12）对指标进行归一化。

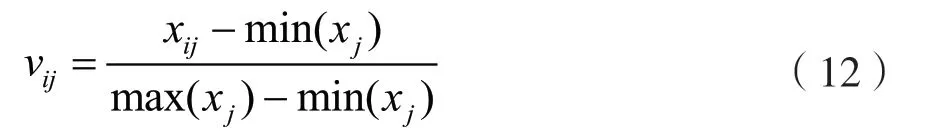
式中，max(xj)和min(xj)分别为在指标j下所有对象的最大值和最小值，且满足0 ≤vij≤1。

（3）计算指标权重。利用式（13）计算指标权重We=(w1,w2,…,wn)：

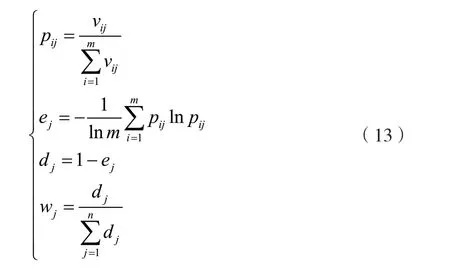
式中，ej是第j项指标的熵值，dj是信息冗余度。

熵权法作为客观评价方法，基于客观数据进行赋权，不受主观因素影响。

2.4 基于组合赋权的熵权-模糊层次分析法

结合传统层次分析法、模糊一致矩阵以及熵权法，提出基于组合赋权的熵权-模糊层次分析法。具体步骤如下。

（1）建立研究对象层次结构模型。

（2）构建优先关系矩阵R。对于矩阵元素，rij=1 时表示因素i比因素j重要；rij=0.5 时表示因素i和因素j同等重要；rij=0 时表示因素i不如因素j重要。

（3）根据矩阵R构造模糊一致矩阵F=(fij)n×n，方法如下。

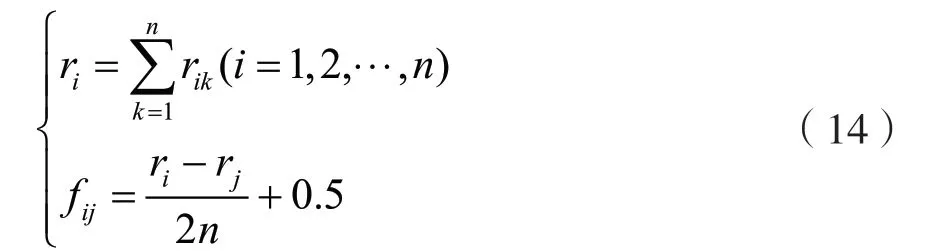
（4）计算模糊层次分析法权值Wf，公式如下：

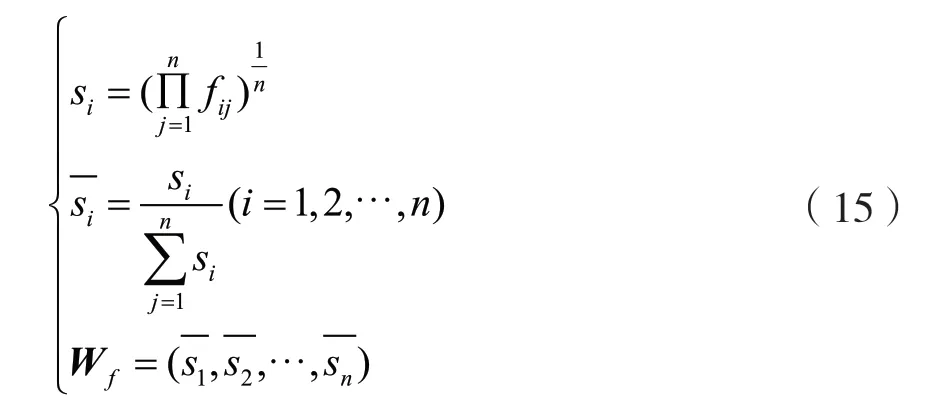
（5）根据评价数据矩阵X，采用熵权法得到权值We。

（6）计算综合权重。采用组合赋权的形式得到综合权重为：

式中，α∈[0,1]为权重线性组合参数。一般情况下α取0.5，即主客观同等重要。

3 战场通信网抗毁性综合评价指标

3.1 典型战场通信网概况

对于一个具有110 个节点、260 条链路的战场通信网进行抗毁性分析，利用节点度数优先攻击策略，即优先攻击网络中度数较高的节点，得到网络抗毁性指标随攻击节点个数变化情况，归一化处理之后的变化曲线如图2 所示，未归一化处理的抗毁性指标数值如表2 所示。

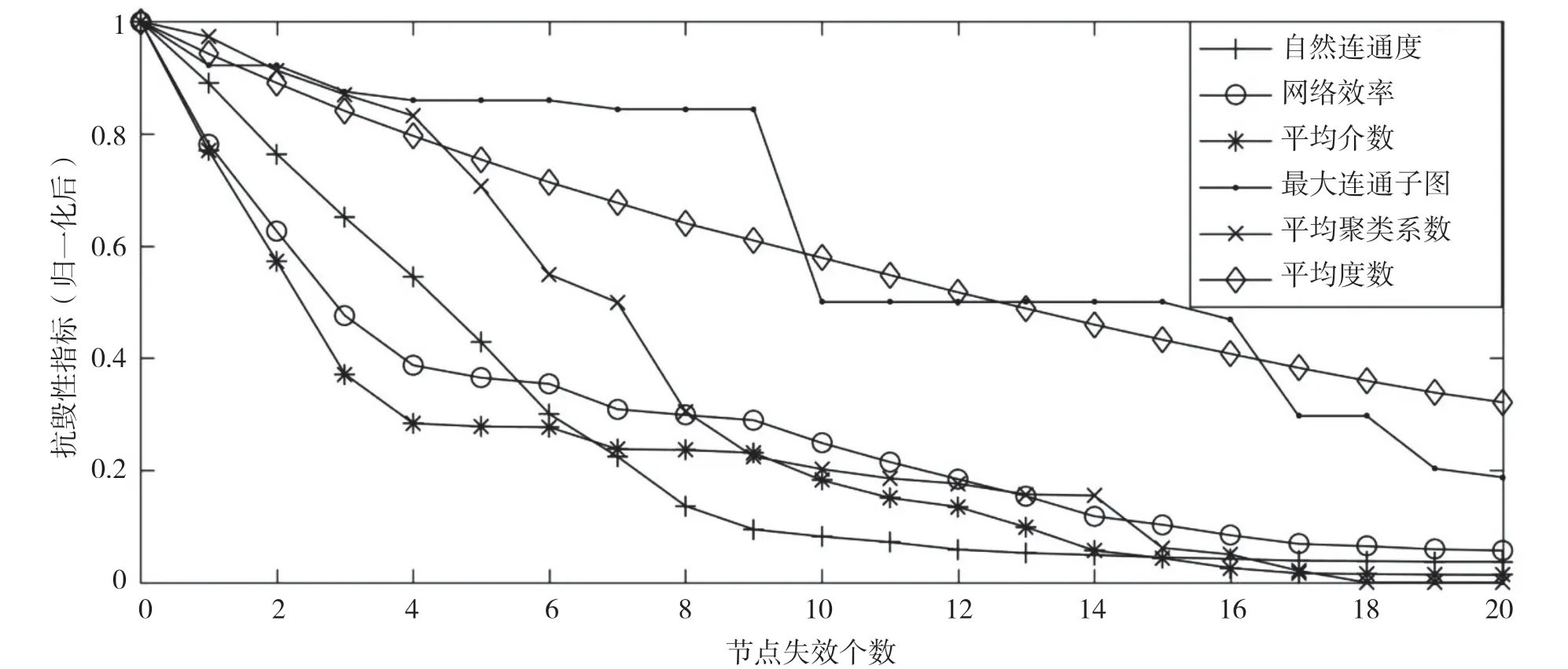
图2 抗毁性指标随节点失效个数变化曲线

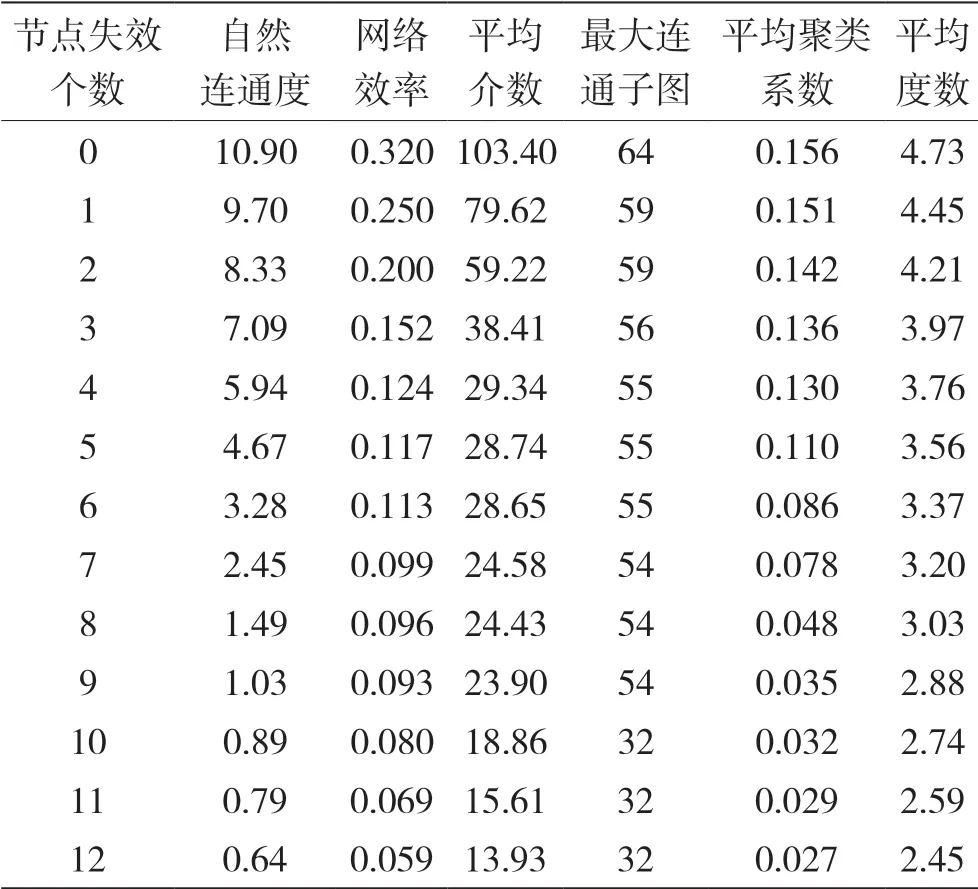
表2 抗毁性指标随节点失效个数变化数值

3.2 基于熵权-层次分析法的抗毁性综合评价指标

利用2.4 节提出的熵权-层次分析法对战场通信网抗毁性指标进行赋权，得到抗毁性综合评价指标，具体步骤如下：

（1）建立战场通信网抗毁性指标层次结构模型。本文仅对指标赋权进行研究，所以只需建立两层模型如图3 所示。

（2）构建优先关系矩阵。通过咨询专家对抗毁性指标两两比较得到优先关系矩阵为：

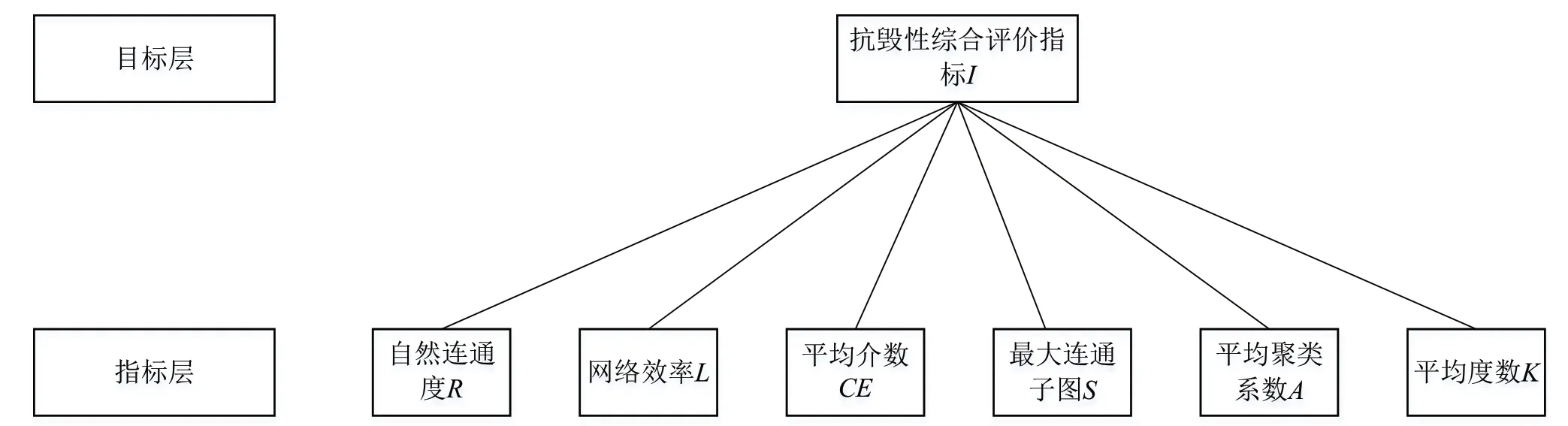
图3 战场通信网抗毁性指标层次结构模型

（3）由矩阵R根据式（14）构造模糊一致矩阵为：

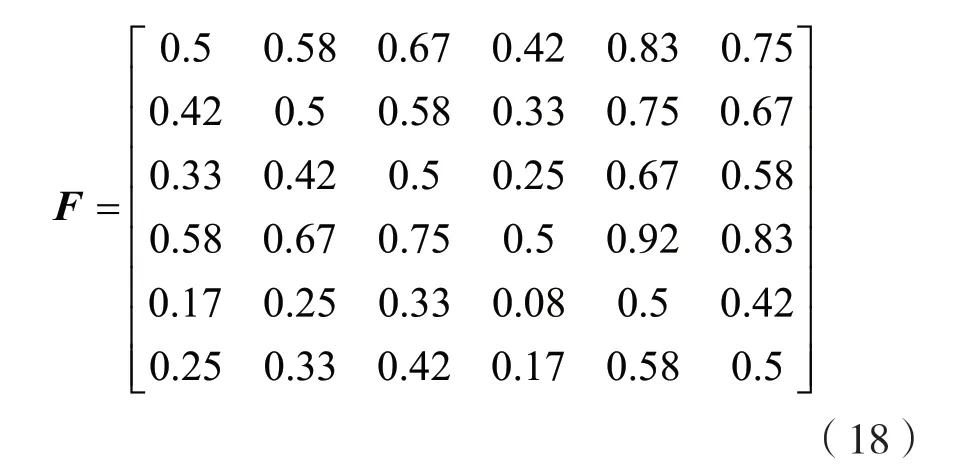
（4）根据式（15）得到使用模糊层次分析法得到的权重为：

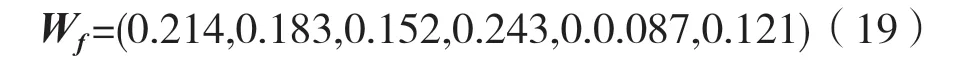
（5）由表2 数据建立评价数据矩阵X，利用2.3节的熵权法得到权重为：

（6）根据式（16）取α=0.5 时，战场通信网抗毁性综合指标权重为：

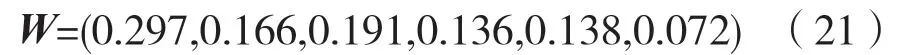
采用传统层次分析法、模糊层次分析法、熵权法以及熵权-模糊层次分析法得到的抗毁性指标权重如表3 所示。

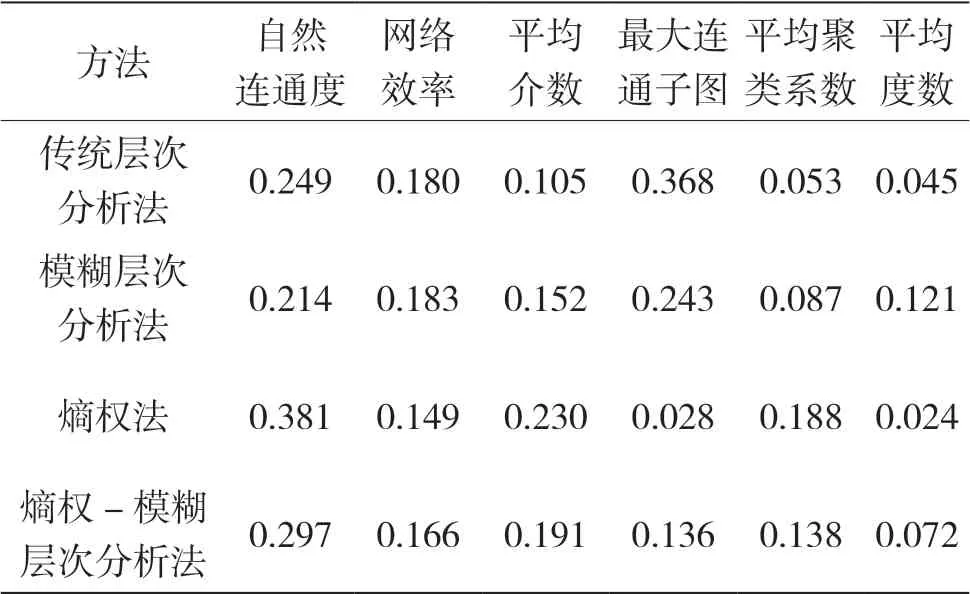
表3 不同方法得到的抗毁性指标权重

对于不同的权重线性组合参数α，得到的战场通信网抗毁性指标权重如表4 所示。

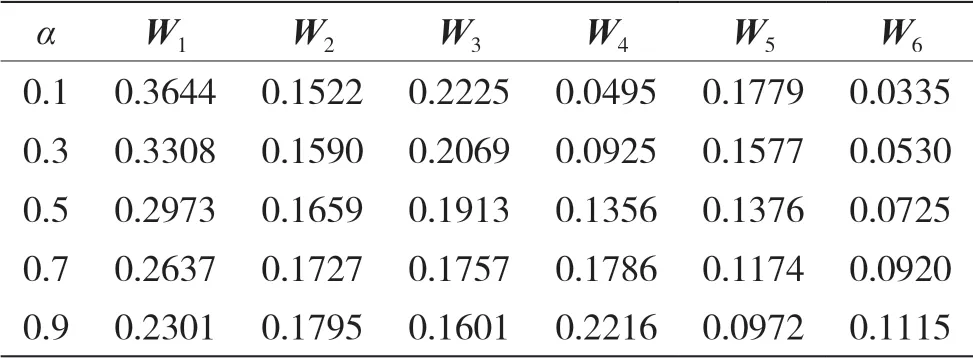
表4 不同线性组合参数的抗毁性指标权重

3.3 基于熵权-层次分析法的抗毁性综合评价指标

模糊层次法得到的指标权重Wf是由专家主观评价得到的，可以看出网络最大连通子图、自然连通度以及网络效率对网络抗毁性影响较大。由表2对比传统层次分析法与模糊层次分析法的结果相差不大，表明提出的模糊层次分析法是有效的。熵权法得到的指标权重We是由指标性质客观决定的，可以看出自然连通度、平均介数以及平均聚类系数对网络抗毁性影响较大，对比图2 与式（20）发现指标变化越大所占的权重也越大，表明了熵权法的有效性。

通过表3 对比层次分析法与熵权法结果，发现抗毁性指标最大连通子图权重差别较大，表明计算指标权重时主客观差别可能较大。式（21）通过权重线性组合的方法得到综合权重指标，同时考虑了主客观因素对指标权重的影响。由表4 知，对于不同的参数α，指标权重也随之动态变化，决策者可根据主观因素重要程度确定参数α；当参数α变化时W1数值相对较大且变化不大，即对单一指标而言，自然连通度能较好地衡量战场通信网抗毁性。

4 结语

结合战场通信网需求特点，重点研究自然连通度、网络效率、平均介数、最大连通子图、平均聚类系数以及平均度数6 种基于拓扑的网络抗毁性指标，提出熵权-模糊层次分析法对指标赋权。该方法相较于传统层次分析法避免了比较判断矩阵不一致问题且降低了算法的计算复杂度，同时采用熵权法削弱主观因素对指标测度的影响。仿真实验表明，所提方法对战场通信网抗毁性指标赋权是有效的，得到的加权抗毁性指标对战场通信网建模优化提供一定的理论建议和支撑。另外，本文所提方法也可拓展应用，当研究对象涉及的影响因素、指标较多时，可使用所提方法建立多层次结构模型进行综合赋权，同时也可使用所提方法对不同网络抗毁性进行综合评价选择性能较好的网络。