应用型本科高等数学课堂教学改革方法浅析

于新艳

（长春光华学院，吉林 长春130031）

利用大约两年的时间，课题组对应用型本科高等数学课堂教学改革进行了系统化和科学化的探索与实践，通过对试点教学班级的实验数据进行统计与分析，课题组初步确定了应用型本科高等数学课堂教学改革的方案与方法。

1 思想政治课有机融入高等数学课堂

思想政治与高等数学从外在来看貌似两门毫不相干的课程，可实质上二者都是哲学的分支体系，属于同宗同源，二者都是高度思维凝练的课程，所以二者内在上并不冲突。不过二者思维方式有所不同，所以在高等数学的课堂中引入思政元素，就要多以数学思维的角度去分析和评论问题。我们采取在课堂上及线上开展时事新闻和热点时政话题的小探讨及评论，教师通过这样的课堂思政方式来了解和掌握学生的思想动态从而引导学生客观地看待、分析和解决问题。

2 有效的课堂设计

高效的课堂教学离不开有效的课堂设计。我们课题组经过反复的摸索，最终确定了如下的课堂教学设计方案。

2.1 复习

高等数学的知识往往是环环相扣，有效地巩固前面所学的知识，才能更好地服务当堂课所学知识。例如：在学习不定积分运算前，先要复习导数及其相关公式，因为二者是互逆的运算关系，在这一复习过程中既把知识体系进行了串联，也开拓训练了学生的逆向思维能力。所以，我们每节课都有复习环节，复习的范畴不一定全是上一节课的内容，而是要考虑到本节课的知识内容与前面学过的知识点间的联系进行相关的复习设计。

2．2 引入

每一节课的内容我们都不是平铺直述，而是要通过适当的方法进行知识的引入。我们高等数学课堂内容的引入方法主要是：例题引入法、几何图形引入法、错题引入法等。一般我们多数采用例题引入法，例如：导数的定义、定积分的概念等的引入都有成型的经典引例，参照这些引例我们对其他内容的引入也都适当配置了典型例题。这样做，使得我们课堂的切入更加具体和形象，便于学生理解和进一步的学习。对于一些理论性强的内容可以适当应用几何图像引入法，如微分中值定理：我们直接把几何图形画出来进行讲解，形象有效地引入定理。错题法则主要在习题课上应用，针对作业、习题有误的问题和题目采用此法引入，使学生明确错在哪里，通过“对”与“错”的对比，加强学生仔细审题与思考的能力。

2.3 讲解与互动

高等数学课堂与文史类课堂最大的区别在于讲解与互动环节，高等数学课堂往往是老师一个人的“独角戏”，而文史类课堂则是师生的“对手戏”，所以如何设计课堂讲解互动环节成了高等数学课堂打破教师“独角戏”模式的一个关键点。根据注意力曲线规律，我们采取1-2-3的课堂互动模式：“1”是指从引入本节课内容开始，教师先讲解10分钟左右，在学生专注力平稳期即将到来时设计互动一次；“2”是指教师利用20分钟左右精讲完本节课重点内容后，在学生专注力开始下降的初始设计互动2次；“3”是指在学生专注力低潮期互动3次。这一互动模式是为了有效提升学生课堂专注力，互动内容有问答及讨论，互动对象是学生个体或小组，每次互动时间控制在2分钟以内。

2.4 课堂小结

以往我们认为课堂小结就是对当堂课程内容的概括，而实际并非如此简单。课堂小结是课堂教学很重要的一环，它既是当堂内容梗概的梳理与总结，也是引发学生思考、预习及复习的重要引导环节。课堂小结相当于写作文扣题段落一样，首尾呼应，并能“承上启下”才最好。所以我们对每一节课的小节都做了精心的设计。例如：我们在完讲一阶导数求导方法这部分内容，小节时我们自然会启发学生联想到：一阶导数（导函数）仍是函数，那么它是否可以再求导数？它的导数如果存在，如何定义？这样小节就为高阶导数的引入埋下了伏笔，同时也使学生加深了对导函数的认识。

2.5 积极地课后复习与练习

课后往往被视为非课堂环节，实则不然。课堂的45分钟想让学生全部“吃”透所学内容是不现实的，学生课下有效地复习与练习是高等数学课堂教学必不可少的一环。我们采取课后教师在线（免费）指导学生有目的、有针对性地复习与练习，督促学生学会自主地学习，积极地思考，教师利用线上这一辅助模式时时帮助学生解决学习上的盲区与难点，这同时也是我们高等数学课程线上线下混合式教学建设的一部分。

这样5步课堂教学环节构成了如下的一个

教学闭环设计见图1。我们每一堂课都按这样的闭环设计进行完整的高等数学课堂教学，这样就形成了我们高等数学课堂教学的良性循环。

图1 教学闭环设计

3 影响课堂教学的因子的量化研究

影响课堂教学的主体因素是课堂教学的两大主体：教师和学生，我们把这二者对高等数学课堂教学的能动性定义为影响课堂教学的因子。我们设教师的能动性这一影响因子为k1（0＜k1＜1），学生的能动性这一影响因子为k2（0＜k2＜1），学生的平时成绩为X1（0＜X1≤100），学生的期末卷面成绩为X2（0＜X2≤100），学生最终的总评成绩为Y（0＜Y≤100），则我们最终成绩评定公式由Y=0.4X1+0.6X2（这是我校目前的期末成绩总评公式）改为：

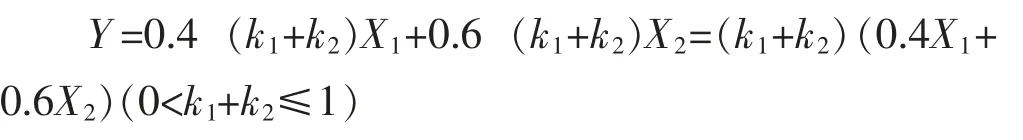
这个公式体现了教师与学生这两大主导课堂教学因素的量化关系。不难发现，以往我们是假设k1+k2=1，而实际上k1+k2往往小于1，这是导致学生高等数学成绩标准差往往偏大或偏小的主要原因。在课堂教学中，我们尽可能地使k1+k2趋向于1，那么k1，k2分别取多少更合适呢？经过我们近两年的课堂教学改革观察：当k1≤k2时更能降低师生彼此影响的负效应，从而提升课堂教学的有效性。通过对这个公式的研究，我们发现在学习高等数学的过程中，学生占主导地位，教师要养成为学生“服务”的意识，让k2增大，也就是激励学生参与课堂教学的能动性，教师则起到带头指路的作用。

4 高等数学在专业课领域应用性问题的课堂教学开展

学习最终的目的是为了用，高等数学作为公共基础课程，其主要目标之一就是服务于各个专业课领域。近年来，我们在高等数学教学和课改方面一直在探讨高等数学的应用性问题，目前，我们在高等数学应用方面已经形成了两大主要应用分支，一是课堂上涉及到物理、工学和经济学方面的运算应用；二是数学建模课程的开展。显然如果在课堂上我们把高等数学的应用问题融合得好，那么不单单是服务于专业课程的需求，也为后续的数学建模课程的开展奠定了坚实的基础。

综上所述，解决高等数学课堂教学的主要点在于“人”，教师有效地引导加上学生主动地参与，结合有效的课堂设计方法，融合思政元素和线上教学元素，一定可以打造高效的应用型本科高等数学课堂教学体系。