冗余喷涂机器人的帕累托优化解集流形分析

易强　吴加富　宋子瑜

摘  要：针对冗余喷涂机器人逆运动学优化解空间难以确定的问题，提出一种基于帕累托优化解集的解流形分析方法，对喷涂机器人逆运动学解流形在解空间中的优化分布问题进行了研究。帕累托优化解集一方面将喷涂冗余机器人的解空间流形与数学中帕累托解集联系起来，另一方面将喷涂冗余机器人的关节逆运动学拓展到数学领域的解空间流形进行研究，更易得到具有物理和几何意义的结论。最后通过空间旋转壳体逆运动学仿真证明了所用方法的合理性。

关键词：冗余机器人  帕累托  流形  优化

中图分类号：TP242.2          文献标识码：A            文章编号：1672-3791（2021）02（a）-0052-04

Manifold Analysis of Pareto Optimization Solution Set for Redundant Spraying Robot

YI Qiang1，2  WU Jiafu2  SONG Ziyu3

（1.Suzhou Ruisai Precision Tools Co.， Ltd.， Suzhou， Jiangsu Province， 215104 China;2.Suzhou Funaair Technology Co.， Ltd.， Suzhou， Jiangsu Province， 215009 China;3.School of Automation， Beijing Institute of              Technology， Beijing， 100102 China ）

Abstract： Aiming at the problem that the inverse kinematics optimization solution space of redundant spraying robots is difficult to determine， a solution-manifold analysis method based on the Pareto optimization solution set is proposed to solve the optimization distribution problem of the inverse kinematics of the spraying robot in the solution space. On the one hand， the Pareto optimization solution set links the solution space manifold of the spraying redundant robot with the Pareto solution set in mathematics， and on the other hand， it extends the joint inverse kinematics of the spraying redundant robot to the solution space flow in the field of mathematics. It is easier to get conclusions with physical and geometric significance by studying the shape. Finally， the inverse kinematics simulation of the space rotating shell proves the rationality of the method.

Key Words： Redundant robot; Pareto; Manifold; Optimization

噴涂机器人在工业应用领域越来越广，尤其是在条件复杂，障碍物较多的工作场所一般需要关节较多的冗余喷涂机器人，而冗余喷涂机器人有无数个逆运动学解，在所有逆解中找到符合条件的最优化逆解成为冗余喷涂机器人工作中的关键问题[1-2]。流形是目前描述机器人逆运动学最高效的理论与方法，帕累托优化解集又是优化解流形的集中描述[3]。

该文针对旋转喷涂工作曲面的冗余机器人，在空间流形基础上提出算法，帕累托优化解集在李群流形基础上分析了冗余喷涂机器人的关节构型空间优化解集，帕累托优化解集一方面将喷涂冗余机器人的解空间流形与数学中帕累托解集联系起来，另一方面将喷涂冗余机器人的关节逆运动学拓展到数学领域的解空间流形进行研究，更易得到具有物理和几何意义的结论[4-5]。通过MATLAB仿真得到了冗余喷涂机器人在不同臂形标志下的自运动流形仿真，最后通过喷涂壳体的仿真证明所用方法的正确性[6]。

1  帕累托优化流形分析

基于机器人运动关节空间的多目标优化性能泛函有如下数学描述：

（1）

式（1）中，表示为目标函数，代表冗余喷涂机器人的解空间向量，M表示为高维空间流形，该文中n=8，分别代表关节运动的下限和上限，冗余喷涂机器人解流形的多目标优化函数之间一般来说是相互冲突的，很难找到唯一的优化解，因此通过流形降维理论优化出的逆解应该是一个最优解集，数学上称之为帕累托（Pareto）最优解集。

1.1 帕累托最优解

如果机器人解空间M中的解θ是非劣的，那么解θ属于帕累托最优解，帕累托最优解之间没有差别      关系。

1.2 帕累托所有最优解组成的集合成为帕累托最优解集

（2）

定义关节构型空间：

（3）

式（3）中，C1为移动关节构型空间，C2到C7为六自由度机械手各转动关节空间构型，C8为旋转空间构型，当壳体运动时，冗余喷涂机器人将会呈现出曲面流形的结构，它包括了冗余机器人的全部逆解。

定义位置关节构型空间：

（4）

定义位置关节工作空间流形：

（5）

式（5）中，low是从基座标系原点到冗余喷涂机器人腕点的矢量，，Cwl为位置关节      流形。

定义姿态关节构型空间：

（6）

定义姿态关节工作空间流形：

（7）

式（7）中，代表末端工具坐标系的姿态，，表示为姿态工作空间      流形。

2  流形分析优化

基于冗余喷涂机械手解流形的局部线性嵌入优化算法有如下表达。

以右上臂形位置关节空间仿真流形为例简述流形优化的基本过程：

（1）给定样本数据集，根据样本数据点的欧氏距离找到每个点的k个相邻空间，Ti为样本数据点的k个邻域下标集合。

（2） 得重构权值矩阵：

（8）

权值集中体现了样本数据点θt对θi在重构数据点时的贡献大小，如果θt不是θi的邻近数据点，则=0。所以重构权值矩阵W是以最小二乘算法最小化每一个样本数据点的重构误差来实现的。针对样本点的旋转特点和缩放特性可以保持重构权值矩阵保持不变，为了能使重构权值矩阵的平移数据保持不变，对所有θi进行权值约束：

（9）

利用拉格朗日乘子算法可以得到重构權值矩阵W的封闭解。

（3）低维嵌入θ'的求解，算法要求其低维嵌入及其邻近点可以反映θ空间中相对应样本数据点的重构权值关系，即最小化损失函数：

（10）

针对加入约束：

（11）

可得：

（12）

式（12）中属于n×n矩阵，要使代价函数取最小值，低维嵌入θ'应该取M的特征值对应的特征向量：

（13）

3  流形仿真验证

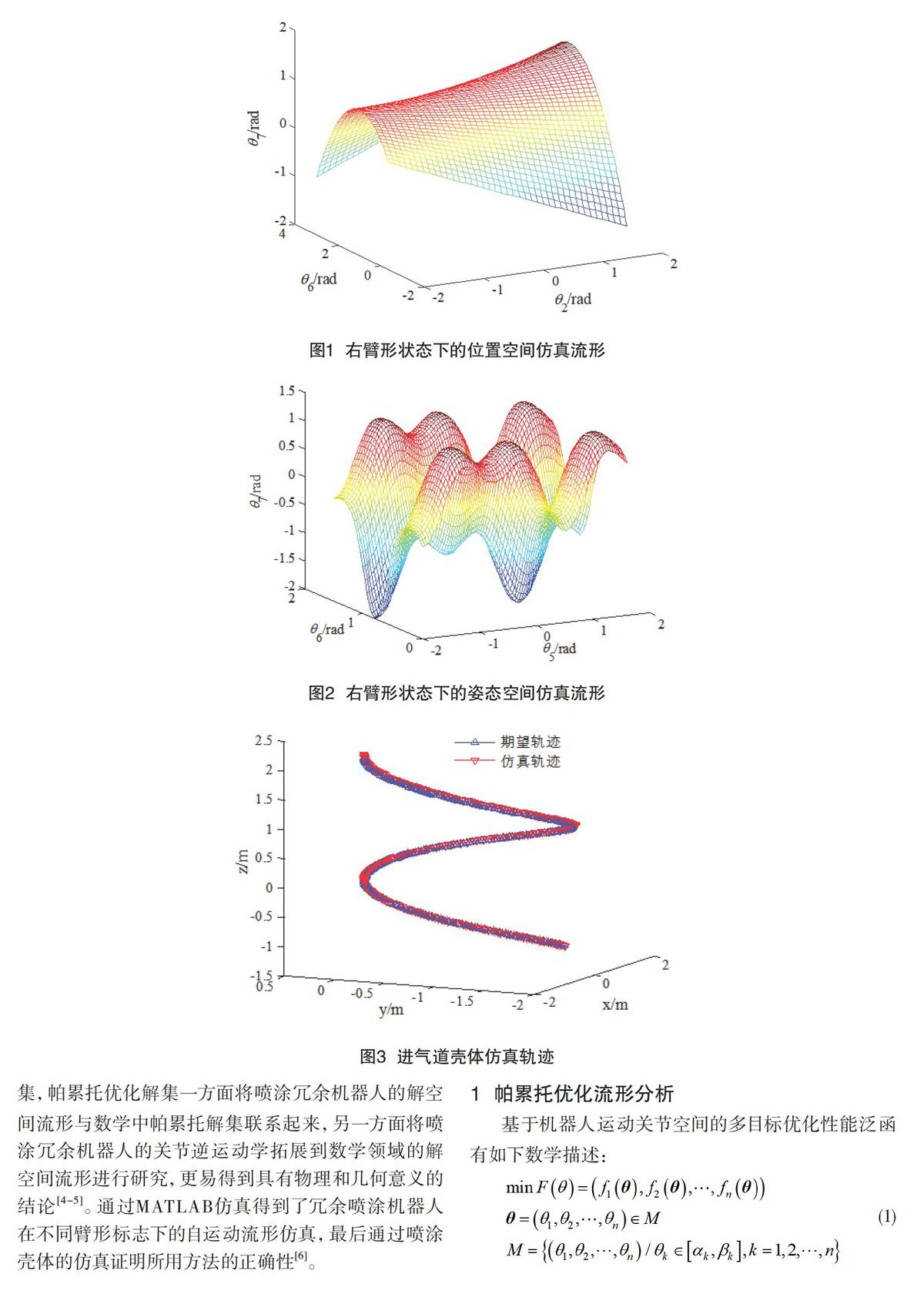
冗余喷涂机器人在各个臂形标志下都有其不同的灵活工作空间，不同的灵活工作空间对应不同的优化解流形，从而其帕累托优化解集也不一样，考虑到右上臂形一般是喷涂冗余机器人在实际喷涂工作中所处的臂形，所以该文针对右上臂型分别在位置空间和姿态空间做了相应的自运动流形仿真，分别见图1、图2。

为了验证所得流形的正确性，该文利用进气道旋转壳体进行仿真来验证所得结论的正确性，进气道旋转壳体具有非常复杂的曲面外形，对逆解流形的计算精度有很高要求，如仿真点位和实际点位高度吻合，则证明算法是可信的，如果误差较大则仿真曲线将会偏离实际曲线较大，具体见图3，冗余喷涂机器人期望轨迹和仿真轨迹高度吻合，充分证明所得运动学逆解流形是正确的。

5  结论

本文针对冗余喷涂机器人关节空间所得位置逆解和姿态逆解，基于帕累托解集最优化理论提出一种流形优化算法，所有优化逆解构成机器人解空间的帕累托优化解集，流形优化方法主要目的在于发现嵌入在高维数据空间中的低维流形结构，数据原始几何特性保持不变。通过仿真得到最优解集的位置关节流形和姿态关节流形。最后以喷涂壳体为例进行仿真验证了所用方法的合理性。

参考文献

[1]徐朋，赵东标，应明峰等.8自由度喷涂机械手的自运动流形分析[J].东南大学学报（自然科学版），2017， 47（2）：254-258.

[2]裴九芳，许德章， 王海. 基于旋量理论的三指机器人灵巧手逆运动学分析[J]. 中国机械工程， 2017（24）：2975-2980.

[3] Nassim A， Abderrahmane A. Boosting scores fusion approach using front-end diversity and adaboost algorithm， for speaker verification[J]. Computers and Elec Engineering， 2017， 9（2）： 1-15.

[4] Krakowski K A， Machado L， Leite F S， et al. A modified casteljau algorithm to solve interpolation problems on stiefel manifolds[J]. Journal of Computational and Applied Mathematics， 2019， 311： 84-99.

[5] Meng L， Breitkopf P， Le Quilliec G. An insight into the identifiability of material properties by instrumented indentation test using manifold approach based on P-h curve and imprint shape[J]. International Journal of Solids and Structures， 2019， 106： 13-26.

[6] Sandoval J， Su H， Vieyres P， et al. Collaborative framework for robot-assisted minimally invasive surgery using a 7-DOF anthropomorphic robot[J]. Robotics and Autonomous Systems， 2019， 106： 95-106.