高频变压器漏电感简化计算方法

叶志军， 谭锴佳， 于旺， 林晓明， 罗继亮， 胡特

(1.华侨大学 信息科学与工程学院，福建 厦门 361021；2.国网株洲供电公司，湖南 株洲 412000；3.湖南联众科技有限公司，湖南 娄底 417000)

0 引 言

高频变压器(high frequency transformer，HFT)，通常是指通过电力电子技术和高频磁链技术实现输入与输出电气隔离和电能变换的小型变压器[1]。由于跟传统变压器相比较，HFT具有频率高、体积小、重量轻和功率密度高等特点，因此其广泛应用于电源和电力电子变压器当中，并在新能源发电和电动汽车等新兴领域具有广阔的应用前景[2,3]。

但是，随着工作频率的提高，HFT寄生参数的影响不容忽视，漏感与分布电容之间形成回路向外辐射能量形成电磁干扰[4-5]。高频工作条件下为了减小开关损耗和噪声，需要利用HFT的漏感作为谐振电路的电感实现软开关[6]。但是漏感非常小将无法实现软开关，漏感太大会导致开关管在关断瞬间承受很大的反向电动势，造成开关管损坏[7]。因此在HFT设计阶段准确而快速的计算HFT漏感参数对HFT乃至于整个变换器来说都是至关重要的[8]。

然而，传统算法没有考虑漏磁分布的频变特性，认为绕组区域的磁场呈简单的线性变化，因此传统方法计算误偏大，难以满足设计要求[9-10]。针对这一问题，文献[11]Dowell推导了高频损耗的计算公式，并通过绕组阻抗公式虚部得到了漏感参数的解析模型，但当绕组孔隙率小于0.7时计算误差较大。文献[12]和[13]基于Dowell公式分别将绕组区域的漏磁能量分为3区和5区，然后推导了单层和多层HFT漏感精确计算公式，计算精度较高但推导过程繁琐。文献[14]基于前者考虑了绕组的曲率效应，增加拐角漏磁计算，采用能量法推导了HFT漏感计算公式，虽然提高了计算精度，但降低了通用性，结论公式复杂，计算量大，在实际工程中难以使用。文献[15]为了提高计算速度和公式通用性，采用磁链法并假设磁通与其所在绕组不交链或全交链，然后分别计算取平均值来简化计算公式，但实际应用过程中计算依旧比较复杂，且上述方法都没有考虑绕组结构，仅适用于叠层绕组HFT漏感计算。

本文在研究HFT绕组区域漏磁空间分布频变特性的基础上，分析了变压器漏感分布的结构特性。并基于磁链分割思想和等效变化原理，提出了一种新的HFT漏磁分布模型和漏感计算方法。最后基于该方法推导了计算公式，并通过仿真模型计算和样机实物测量证明了该方法的准确性和可行性。

1 高频变压器漏感计算原理

漏磁是指单独和原边或副边绕组匝链的磁通。在HFT中，一个绕组电流产生的漏磁通存在于绕组绝缘层与导体内且不和另一个绕组相交链。漏磁存储磁场能量，该效应可以用漏感参数Lk来体现。漏感与磁芯窗口内漏磁场强度H密切相关。而HFT绕组受到自身和邻近绕组产生的高频磁场作用，在导体内存在严重的高频涡流，进而形成严重的集肤效应和邻近效应[16]。涡流分布取决于频率、绕组布置方式等，其直接影响绕组电磁参数的空间磁场分布[17]。如图1所示，HFT绕组区域磁通密度B空间分布具有复杂的频变特性。

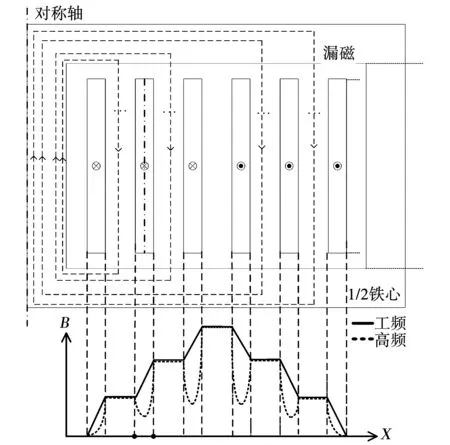
图1 磁芯窗口内不同频率的磁通密度分布图Fig.1 Magnetic flux density distribution profile within the transformer window at different frequencies

按计算原理不同，HFT漏感计算可分为磁链法和能量法，其计算原理如下：

(1)

(2)

式中:I为绕组电流；μ表示绕组磁导率；n表示绕组层数；N表示每层匝数；S表示漏磁面积；V表示漏磁体积。

磁链法通过计算绕组间隙和绕组导体内的漏磁链，以及磁链和电感的关系求得漏感。能量法通过计算绕组间隙和绕组导体内的漏磁能量，以及磁场能量和电感的关系求得漏感。两种方法本质都基于电磁场基本公式，并无优劣之分，代入相同的漏磁分布模型计算并考虑部分匝链，最终两种方法所推导出的结论公式是一致的[15]。

有限元计算法在仿真软件涡流场分析下对HFT进行电磁场数值扫频计算，得到变压器各个绕组的自感L、互感M以及耦合系数k，通过下式分别计算出初级和次级绕组的漏感：

(3)

(4)

式中：k表示耦合系数；M表示互感；L1和L2分别表示一二次侧自感。

但这种方法难以建立解析计算公式，在有限元软件中进行建模计算，不满足工程设计上快速计算的要求。

工程上通常采用短路试验测量变压器的漏感。其实验原理如图2所示，将副边绕组短路，由于漏感远小于励磁电感Lm和电阻Rm，励磁支路被认为开路，从原边绕组测量的电感值近似为变压器的原副边的总漏感值[18]。变压器漏感解析公式的推导也是在这种假设下进行[19-20]。

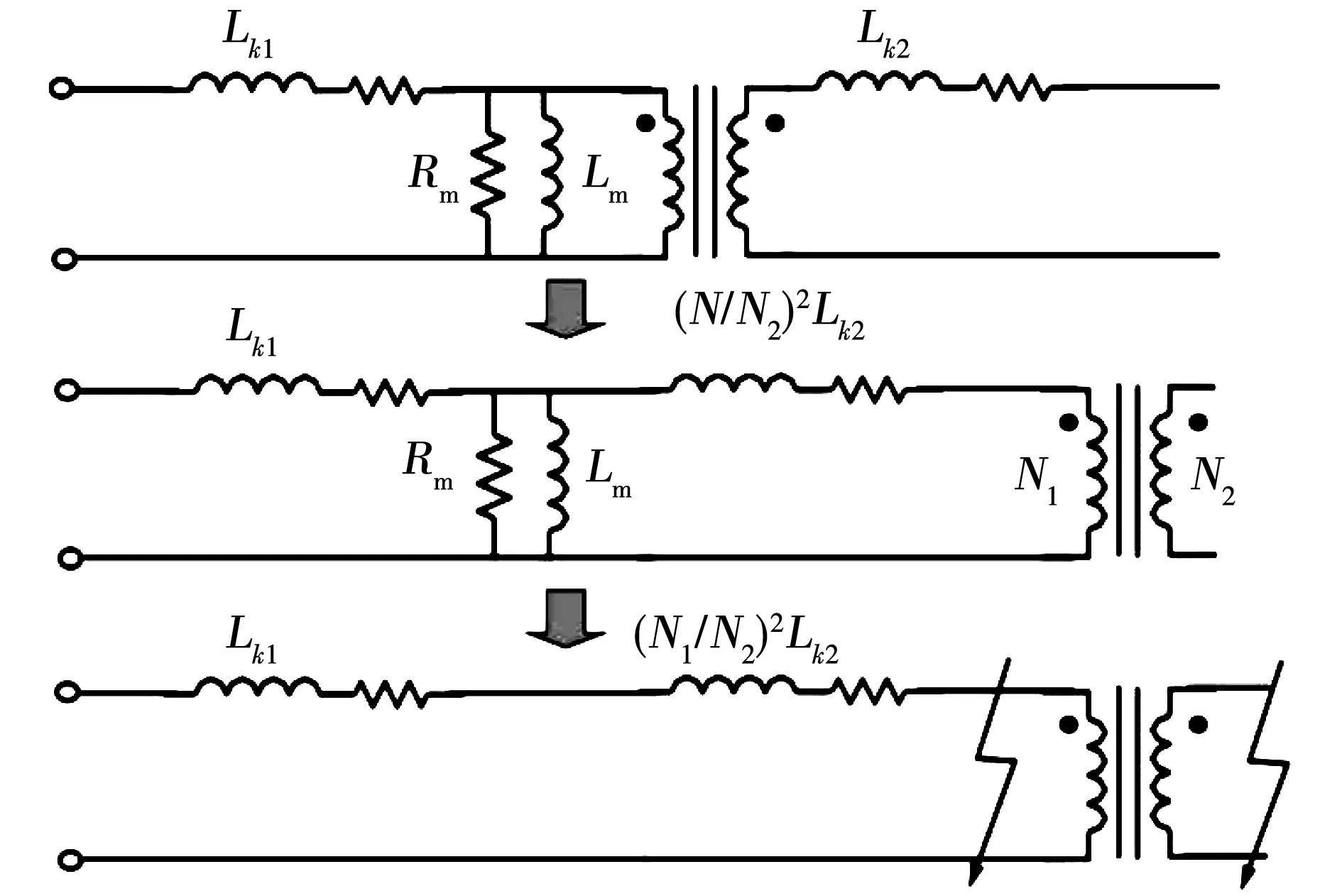
图2 短路实验测量变压器漏感原理图Fig.2 Principle of measuring transformer leakage inductance by short circuit experiment

图3 高频变压器绕组结构示意图Fig.3 Schematic diagram of winding structure of high frequency transformer

2 高频变压器漏磁分布模型

2.1 经典漏磁分布模型

图4为传统叠层式n层双绕组HFT结构示意图。传统算法将低频磁通密度分布曲线作为漏磁分布模型计算HFT漏感，认为绕组导体漏磁密度线性增大，绕组间隙漏磁密度均匀不变，即HFT绕组区域磁场强度按梯形线性分布。根据磁路全电流定律得到绕组间隙和绕组导体的漏磁密度表达式：

(5)

(6)

(7)

式中：d该层绕组的厚度；h为该层绕组的高度；Bm和Bw分别为第n层绕组层外侧间隙和内侧间隙的漏磁密度；Bx为第n层绕组层导体内某点的漏磁密度，其中0≤x≤d。

经典漏磁分布模型不考虑高频涡流效应，认为漏磁通密度在磁芯窗口内沿导线绕制方向呈线性变化，结合变压器结构参数可直接计算出漏感，优点是解析计算式简便，缺点是忽略了高频涡流效应，高频下变压器漏感计算误差较大。

2.2 实际漏磁分布模型

对于多层绕组HFT由安培环路定理可得间隙层的漏磁分布模型。而绕组导体层实际漏磁分布模型较为复杂，对同心双绕组HFT应用麦克斯韦方程和媒质方程得到所需形式的修正麦克斯韦方程组：

(8)

▽×B=μσE。

(9)

因为Bw和Bm分别平行于绕组导体层内外表面，所以Bw和Bm与z无关。由于HFT几何对称，导体层内电磁强度E和漏磁密度B满足下式：

(10)

(11)

式中E仅含y分量，B仅含z分量，所以E和B只是x的函数。则式(8)和式(9)可简化为：

(12)

(13)

将式(13)导入式(12)得到二阶微分方程

(14)

式(14)是一个修正贝塞尔方程，其通解为

B(x)=CI0(αx)+GK0(αx)。

(15)

其中α=(1+j)/δ为传播系数,δ=(2/ωμγ)1/2为集肤深度，ω=2πf为角频率，γ为导体电导率。将绕组边界条件式(5)和式(6)代入式(15)可得通解系数：

(16)

(17)

假定αx>>1，则修正贝塞尔方程渐进形式简化为：

(18)

假定(xmxw)≈(xmx)≈(xwx),其中x∈(xw,xm)，将式(16)、式(17)、式(18)代入式(15)中后可得绕组导体的漏磁实际分布模型。

(19)

由于其中xm-xw=d，因此设xw=0、xm=d，化简后可得绕组导体的漏磁密度分布表达式为

(20)

相比式(7)的线性分布，式(20)表示为双曲函数的非线性分布，更加贴近漏磁实际分布。

2.3 漏磁分割法基本思想

考虑到实际漏磁分布模型公式较为复杂，求解的过程不仅涉及复变量和双曲函数，还需对其平方再进行积分运算，求解过程繁琐，结论公式复杂，计算量较大，实际工程中较难使用。因此，针对n层双绕组隔离HFT，基于等效变换原理，本文采用漏磁分割法和面积补差法重新建立漏磁分布模型，并采用分区计算绕组区域漏磁链的方法简化HFT漏感计算解析表达式。

图4 高频变压器绕组区域漏磁分布模型示意图Fig.4 Schematic diagram of flux leakage distribution model in winding area of high frequency transformer

图4所示为漏磁分割法计算漏感的原理示意图。这里以实际漏磁分布曲线代表HFT绕组区域真实漏磁分布，而其他模型的分布曲线与实际漏磁分布曲线所包围的面积表示为其与真实值的误差面积。从图5可以出看出传统法的误差面积(S7～S9)很大，因此传统法计算误差大。而分割法的误差面积(S1～S6)远远小于传统法，与实际曲线基本吻合。且分割法存在的误差是对非线性分布模型进行线性化等效变换后导致的必然误差。设S1～S6为误差面积，S12、S34、S56为补差面积。通过分析可知对于等效分布模型，当补差面积小于误差面积时，计算值偏大，当补差面积大于误差面积时，计算值偏小。因此，这里可以通过补偿系数Kg=2δ/d≤1来调节误差，即G点选取比实际值更小，让补差面积和误差面积接近。分割法本质是由非线性模型的线性逼近来近似描述漏磁在绕组区域的频变特性，进而从简单的线性系统中得出实际复杂的非线性系统的结论。根据HFT绕组区域实际漏磁分布曲线，通过割点G将绕组导体区域漏磁分割成左半导体层P1和右半导体层P2两部分，并假设高频下P1和P2区域的漏磁都是线性变化的，以等效简单的单折线分布代替实际复杂的双曲线分布。

2.4 等效漏磁分布模型

为了简化漏感计算，得到更为简单结果表达式，对HFT绕组导体区域漏磁实际分布模型采用线性化处理，得到更为简洁的等效分布模型。即在计算中仅考虑导体层中线的漏磁频变特性，而忽略中线两侧的变化。这样一来相比实际漏磁分布模型需要考虑导体层上无数个点的漏磁频变特性，等效后只需考虑三个特殊点，进而简化推导过程和结论公式，把非线性分布变成简单的线性分布模型，将复杂的双曲线换为简单的单折线，最终得到图4实线所示的漏磁分布模型。值得注意的是，分割法变换是一种等效变换，变换前后变压器绕组导体和间隙中的漏磁能量不变。

对于式(20)所示的复杂函数公式，本文用一个简单的分段函数替代。设割点G(Xg，Bg)，左边界点W(Xw，Bw)，右边界点M(Xm，Bm)。为简化推导过程，先求解单层绕组的漏磁密度分布公式，设导体层厚度为d，其中Xm-Xw=d，则有Xw=0，Xm=d，Bw和Bm由式(5)和式(6)可以得到，将Xg=d/2代入由式(20)，则Bg可由下式计算得到：

(21)

(22)

而考虑到等效模型存在的固有误差，通过Bg乘以补偿系数Kg减小误差，提高精度。

已知如图4所示3个点，可以分别求得左半导体层和右半导体层内的漏磁分布函数的斜率分别为：

(23)

(24)

将式(23)、式(24)和点代入直线方程可以得到HFT绕组导体层区域的等效漏磁分布模型表达式为

(25)

这是一个简单的线性分段函数。

3 高频变压器漏感计算方法

传统HFT漏感参数一维解析模型基于Dowell理想变压器模型，假设绕组层高度和磁芯窗口高度基本一致，然而实际工程中，磁芯窗口要安装骨架，并且当采用铜箔绕制时也无法保证绕组高度和磁芯窗口高度一致。因此在实际计算时，假定漏磁为理想分布，所有磁力线都有一个相同的计算高度h′=h/ρ，其中ρ=1-D/πh为洛氏系数，D为漏磁场总宽度，由下式可计算得到：

(26)

将HFT窗口漏感Lk划分为5个部分：原边绕组Lip、原边间隙Ljp、副边绕组Lis、副边间隙Ljs、原副边隔离层Lps。采用分区计算的原则计算各部分漏感，最后叠加即可得到变压器总漏感，即

Lk=Lip+Lis+Ljp+Ljs+Lps。

(27)

能量法的优势在于其默认考虑部分匝链，计算准确但计算复杂，而磁链法可以假设漏磁不匝链(n-1)N，全匝链nN，平均匝链nNx/d来简化计算，计算灵活。为了简化计算，采用磁链法计算HFT绕组导体区域漏感，将式(20)代入式(1)，假设平均匝链，匝链数为nNx/d，求和化简后可得到原边和副边绕组导体层的漏感为：

(28)

(29)

(30)

(31)

式中：dp、Tp、hp、np、Np分别为原边绕组厚度、长度、高度、层数、匝数；ds、Ts、hs、ns、Ns分别为副边绕组厚度、长度、高度、层数、匝数。

将绕组间隙层漏磁密度分布表达式(6)代入式(1)或式(2)可以求得绕组各绝缘层漏感，然后求和可以得到整个绕组间隙区域的漏感为：

(33)

将绕组隔离层漏磁密度分布表达式(5)代入式(1)或式(2)中可以求得原副边绕组隔离层区域的漏感为

(34)

式中:djp为原边绕组间隙层厚度；djs为副边绕组间隙层厚度；dps为原副边绕组隔离层厚度；Tps为原副边绕组隔离层长度。

将式(25)代入式(1)，采用磁链分割法简化考虑频变特性的绕组导体层区域的漏感计算式，即

(35)

(36)

HFT漏感计算的关键在于绕组导体层内的漏感准确与否，式(35)和式(36)采用分割法分别计算绕组左右两半导体层区域的漏磁磁链，可得：

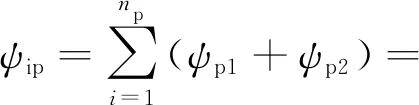
(np-1)(3+β)]，

(37)

(ns-1)(3+β)]，

(38)

(39)

在计算得到了绕组各个区域的漏磁磁链后，将式(32)、式(33)、式(34)、式(37)、式(38)代入式(27)后计算得到HFT总漏感。

4 实验模型与计算方法验证

4.1 实验模型及有限元仿真模型

为了验证新方法的有效性，本文设计并绕制了一台叠层式绕组结构的高频变压器样机，样机绕组采用0.3/15 mm铜箔，原边和副边分别绕3匝，磁芯采用EE40/17/12锰锌铁氧体，骨架采用EE40-PET，绕组间隙隔离层采用0.1 mm绝缘胶带，如图5(a)所示。

为了保证计算精度，使仿真计算值更加贴近实际值，采用Ansoft Maxwell有限元分析软件搭建几何尺寸1∶1的HFT三维仿真模型，如图5(b)所示。为分析频率对HFT电磁参数的影响，研究漏感参数的频变特性，采用涡流场求解器对HFT的模型进行扫频分析，在高频情况下要设置导体的涡流效应，且在设置导体类型时选择Solid作为传导电流实体，实体的路径需要计算表层感应电密分布，从而考虑集肤效应。

涡流场求解器设置以10 kHz为陡度，对10 kHz到100 kHz取10个点对实验模型进行扫频计算。利用场计算器计算短路测试条件下磁芯窗口内绕组及其层间绝缘的漏磁能量，通过漏磁场能量与漏感之间的关系，进而计算出HFT的漏感。也可以通过设置参数矩阵，模型求解后由运算结果可以得到各个频率下原副边各个绕组线圈的电感参数和其电感耦合系数，通过绕组电感、耦合系数与漏感之间的关系，进而计算出HFT的漏感。

图5 实验模型与仿真模型Fig.5 Experimental model and measurement platform

4.2 漏感计算及实验验证

基于相同的漏磁模型，推导漏感公式，磁链法比能量法更加简便。而采用相同的方法，分割法比现代法更简单，比传统法更加准确。表1分别总结了采用分割法归算到变压器一次侧的HFT各区域漏感计算公式。

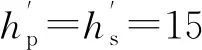
表1 归算到一次侧的各区域漏感计算公式

采用WK6500B阻抗分析仪测量实验样机漏感。变压器原边绕组的引脚之间用夹具电极固定，副边绕组短接，并设定宽频范围内测量电感。最终可以测得等效到原边的等效漏感。在50 Hz～1 MHz宽频范围内测量并计算高频变压器样机漏感，如图6所示为漏感测量平台。

图6 实验模型与测量平台Fig.6 Experimental model and measurement platform

4.3 结果比较与分析

图7为本文提出的基于磁链分割的漏感解析计算方法、传统计算方法、有限元仿真方法与实验测量法在0～1 MHz宽频区间范围内的漏感值对比曲线图。

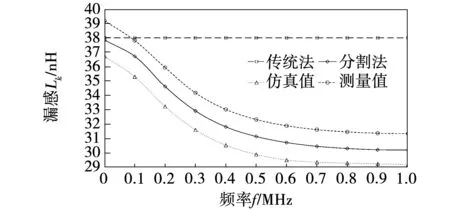
图7 不同计算方法和仿真与测量的对比曲线图Fig.7 Comparison of leakage inductance obtained by the different method, FEA simulation and measurement

分析图7可以看出：1)相较于传统计算方法，分割法的计算值曲线与仿真和测量的变化趋势更趋于一致，计算误差更小，解析公式和仿真模型都满足工程的要求；2)在宽频范围内，计算值与测量和仿真存在误差，这是因为分割法是基于理想条件计算的，其所用的漏磁分布模型为等效的线性分布模型，较实际漏磁非线性分布模型存在一定的偏差。

5 绕组结构对漏感的影响

变压器绕组结构与变压器绕组区域漏磁分布息息相关，在实际工程中为了减小高频变压器漏感，通常采用交叉换位技术将绕组绕制交错式和夹心式绕组结构。

5.1 交错式绕组结构

对于交错式绕组结构的变压器，假设其原副边共n层，m级交错，当m=1时，为1级交错，即完全交错。将变压器绕组的所有导体层分成n/m个部分，每部分m层原边导体和m层副边导体。如图8所示。这样就把复杂的n层交错式多绕组结构变压器漏感计算简化为了简单的m个叠层式双绕组结构变压器漏感计算。

将绕组线圈的结构理想化，设绕组平均匝长为T，即Tp=Ts=Tps=T,Np=Ns=N,djp=djs=dj,dp=ds=dl,hp=hs=h,np=ns=n，则交错式绕组高频变压器的漏感可以简化为

(m-1)(3+β)]。

(40)

频率设置为0.1 MHz，二级交错，导体厚度dl=0.8 mm，间隙厚度dj=0.1 mm，绕组层数n=4，每层匝数N=1，绕组高度h=15 mm,平均匝长T=68 mm，代入式(40)得变压器漏感为12.3 nH。

图8 交错式绕组结构的漏磁密度分布图Fig.8 Magnetic flux leakage density distribution of interleaved winding structures

5.2 夹心式绕组结构

对于夹心式绕组结构的变压器，可以将绕组部分分为两个n/2层的层叠式双绕组结构，如图(9)所示。设n/2=x，并对变压器绕组做上述同样理想化简化，则交错式绕组高频变压器的漏感可以简化为

(x-1)(3+β)]。

(41)

频率设置为0.1 MHz，导体厚度dl=0.8 mm，间隙厚度dj=0.1 mm，绕组层数n=4，x=2，每层匝数N=1，绕组高度h=15 mm，平均匝长T=68 mm，代入式(40)得变压器漏感为29.9 nH。

5.3 分析与比较

基于上面第4节模型准确的前提下，利用Ansoft Maxwell有限元分析软件改变变压器绕组结构，建立如图10所示不同绕组结构变压器的有限元仿真模型。图10(a)、10(b)和10(c)分别为叠层式、夹心式和交错式绕组结构的漏磁能量分布情况，由图11可知，绕组交叉换位后，绕组内部磁场强度降低，漏磁能量减小，由式(2)可知，这必然导致变压器漏感减小。

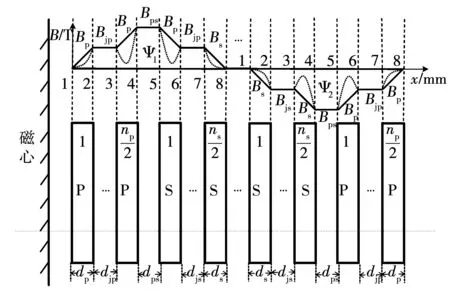
图9 夹心式绕组结构的漏磁密度分布图Fig.9 Magnetic flux leakage density distribution of sandwich winding structures

图10 三种绕组结构Fig.10 Three winding configurations

图11 磁芯窗口内磁场能量分布Fig.11 Leakage energy distribution in core window

图12为不同绕组结构高频变压器在宽频范围内的漏感分布曲线，表2为不同绕组结构高频变压器漏感的计算值和仿真值。由图12和表2可知，夹心式相较于叠层式，变压器漏感减小约64%，而交错式相较于叠层式和夹心式，变压器漏感分别减小约79%和41%。通过交叉换位技术改变高频变压器绕组结构，不但可以显著减小高频变压器漏感，同时还能削弱频率对漏感的影响，减缓高频变压器的频变特性曲线。

表2 不同方法的漏感计算值

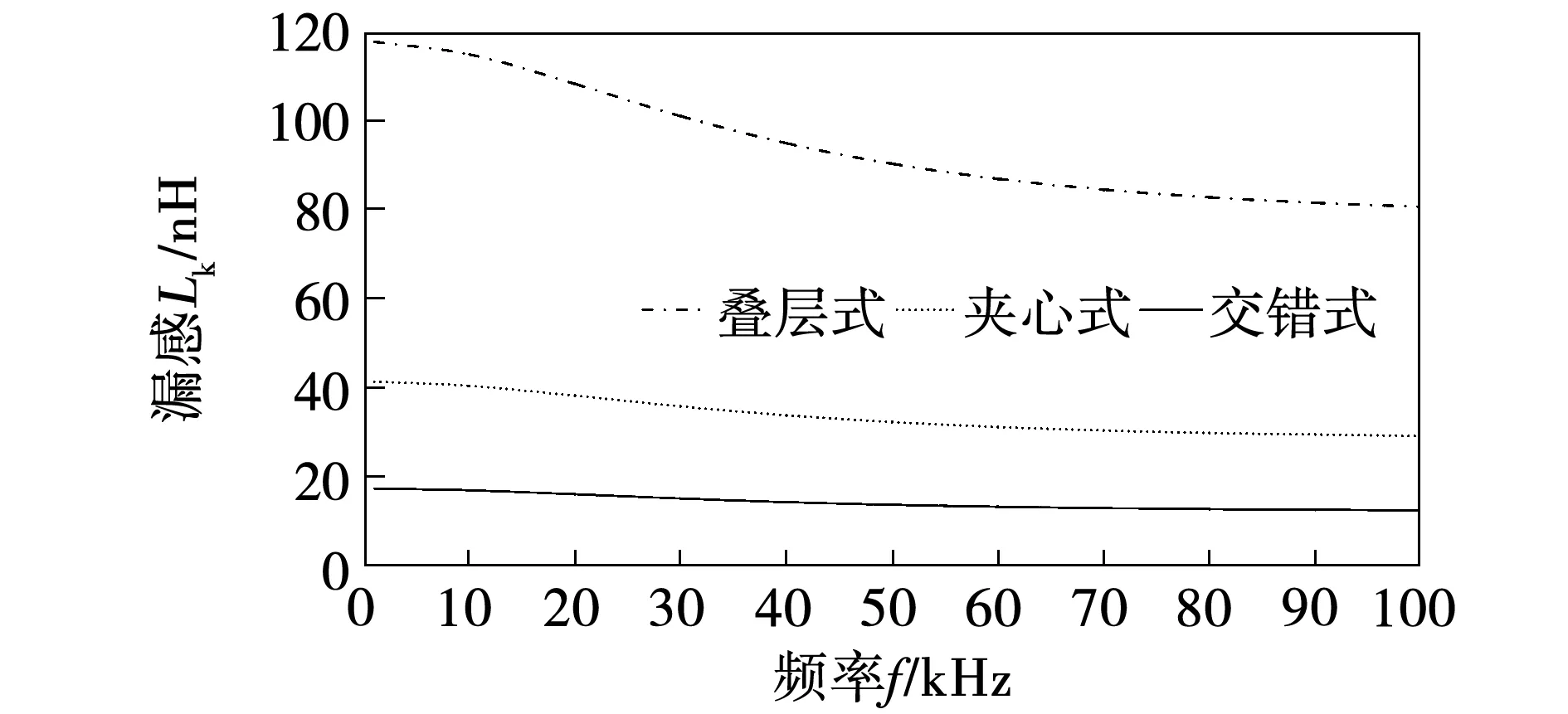
图12 不同绕组结构的漏感对比曲线图Fig.12 Comparison of leakage inductance under different winding configurations

6 结 论

本文分析了应用于电源的高频隔离变压器的漏感参数计算原理与方法。变压器运行频率升高，高频涡流所产生的集肤效应和临近效应影响绕组区域的磁场和电流分布，使其漏磁实际分布较为复杂。而忽略其漏磁频变特性必然导致漏感计算误差偏大，基于实际漏磁分布模型考虑频变特性又会造成计算过程繁琐，计算公式复杂等问题。本文基于磁链分割法建立了高频变压器实际漏磁分布等效变换模型，并给出了计算模型的解析计算表达式，该方法不仅考虑了漏磁频变特性，还考虑了不同绕组结构的分布特性，相较于传统法精度更高，相较于其他方法计算过程更简单，可用于高频变压器漏感参数的快速计算。