横向预应力张拉引起的模架耦合效应分析及简化计算

毕树兵

(中铁十八局集团第五工程有限公司，天津 300451)

满堂支撑架具有搭设方便、实用性强等优点[1,2]，在我国土木工程施工领域得到了广泛的应用[3,4]，目前常用的满堂支撑架有扣件式、碗扣式和盘扣式等，且各种满堂支撑架都有其配套的设计规范[5,6]。对于大跨度超宽箱梁结构多采用三向预应力体系，在落架前多需要进行预应力张拉，结构会因此发生非均匀变形，进而引起荷载在支架内重分布，即模架耦合效应。特别是对于采用满堂支架法现浇施工的大跨度斜拉桥，横向预应力张拉时荷载不能及时转移到桥墩等永久结构上，致使有的立杆会卸载，也有的立杆荷载需求会大幅度增加，如果在支架设计时不能充分考虑，有引发安全事故的风险。为此，本文以保定乐凯大街转体桥为例，根据规范进行了现浇支架设计验算，并建立有限元模型，研究了横向预应力张拉引起的支架内力重分布现象，在此基础上提出了考虑横向预应力张拉模架耦合现象的简化计算方法，可为类似工程提供参考。

1 工程概况

如图1所示，保定乐凯大街转体桥采用(145+240+110)m子母塔斜拉桥结构体系，子塔转体重量35 000 t，母塔转体重量46 000 t。子塔转体部分在支架上分为5段现浇，纵向节段为40 m+40 m+44 m+40 m+40 m，合拢段长度均为3 m。主梁采用三向预应力W型截面薄壁结构，梁顶宽39.7 m，底宽18.0 m，梁高3.5 m；标准段顶板厚30 cm，底板厚35 cm，外侧斜腹板厚40 cm，内侧斜腹板厚30 cm；预应力钢束均采用高强低松弛钢绞线，张拉控制应力均为1 339 MPa。标准段顶板布置M1(7-∅15.2 mm)和M2(7-∅15.2 mm)横向预应力筋，M1和M2交错布置，中腹板布置M4(9-∅15.2 mm)横向预应力筋，具体如图2所示。为确保施工安全，在进行现浇支架设计验算时需要考虑预应力张拉引起的模架耦合效应。

图1 全桥立面(单位：cm)

2 现浇支架设计验算

该桥箱梁采用盘扣式满堂支撑架施工，箱梁标准节段盘扣支架顺桥向立杆间距初步选为150 cm，横桥向90～150 cm，横截面一排支架布置39根立杆，其中底板和腹板下31根，两侧翼缘板下各4根；主龙骨采用12 cm×12 cm(3.5 mm)方钢，横桥向布置，次龙骨采用6 cm×10 cm钢木梁，模板为15 mm厚竹胶板，基础采用30 cm厚C30混凝土硬化，其支架布置断面如图3所示，盘扣支架主要技术指标如表1所示。

2.1 按规范设计验算

根据规范分别取横截面整体和底腹板部位进行支架立杆受力验算。

图2 箱梁断面(单位：cm)

图3 盘扣支架方案(单位：mm)

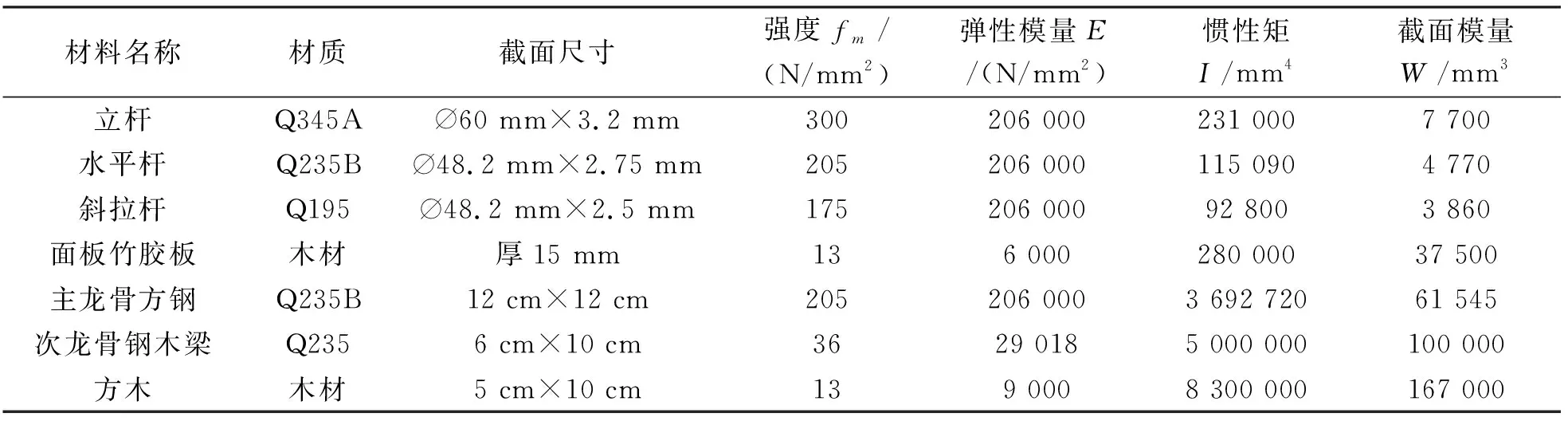
表1 材料特性一览表

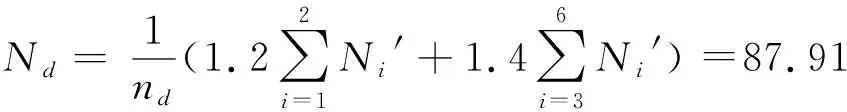
由此可知支架立杆最大轴力设计值为Nmax=Nd=87.91 kN。

(3)立杆承载能力计算：按照《建筑施工承插型盘扣式钢管支架安全技术规程》(JGJ231-2010)5.3.2，盘扣支架立杆计算长度l0=max{ηh,h′+2ka}。式中：l0为支架立杆计算长度(m);a为支架可调托座支撑点至顶层水平杆中心线的距离(m)；h为支架立杆中间层水平杆最大竖向步距(m)，方案为1.5 m；h′为支架立杆顶层水平杆步距(m)，取1.0 m；η为支架立杆计算长度修正系数，取1.2；k为悬臂端计算长度折减系数，取0.7，计算得：l0=max{1.2×1.5 m,1.0+2×0.7×0.4 m}=1.8 m。

参照《建筑施工承插型盘扣式钢管支架安全技术规程》(JGJ231-2010)5.3.3，取强度f=300 MPa；截面积A=571 mm2，回转半径i=2.01 cm，长度l0=1.8 m，长细比λ=l0/i=89.55，稳定系数φ=0.55，计算得立杆承载能力为[N]=φAf=94.2 kN>Nmax=87.9 kN,验算通过。

2.2 考虑横向预应力张拉效应验算

为更好地模拟混凝土浇筑及横向预应力张拉引起的箱梁与模架的耦合效应，建立箱梁与模架有限元模型，考虑混凝土模板与支架的接触效应和预应力张拉作用。模型中主梁C50混凝土采用solid45单元模拟，弹性模量为3.45×104MPa，泊松比为0.2，材料密度为2 650 kg/m3；横向预应力筋采用link8单元模拟，弹性模量为1.95×105MPa，泊松比为0.3，材料密度为7 850 kg/m3；材料的线膨胀系数为1.2×10-5m/℃；预应力筋的抗拉强度值为1 860 MPa；支架立杆采用beam3单元模拟，弹性模量为2.0×105MPa，泊松比为0.3，密度为7 850 kg/m3。支架立杆顶端与箱梁在竖向采用接触单元模拟，立杆顶端设置conta175接触单元，箱梁底面设置targe170目标单元，接触类型为只接触不滑移；支架底端设置全约束。

根据支架的初步设计方案，取立杆纵向间距为150 cm，采用以上有限元模型计算得横向预应力张拉前后箱梁和支架变形如图4所示。由此可知：

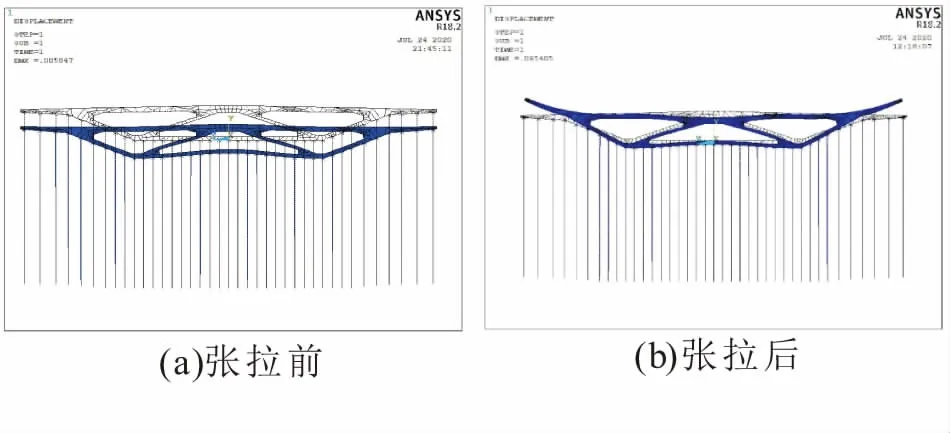
图4 梁体和支架横向预应力张拉前后变形结果

(1)立杆纵向间距为150 cm时，在混凝土浇筑后横向预应力张拉前，采用有限元计算得支架立杆的最大轴力Ne1=83.3 kN(见图5(a))，发生在腹板与翼缘板、顶板相交位置，此处混凝土最厚，比规范简化计算得出的Nmax=87.91 kN略小，有限元模拟与实际情况符合。

(2)横向预应力张拉后，立杆的竖向最大荷载Ne2=110.0 kN(见图5(a))，此时立柱最大荷载发生在腹板与底板相交位置，不仅远大于按规范简化计算得出的Nmax=87.91 kN，而且超过了立杆的承载能力[N]=94.2 kN。

由此可知，在不考虑箱梁横向预应力张拉效应时计算支架竖向受力是满足规范要求的，但考虑横向预应力张拉后支架立杆的最大轴力大幅度增加。虽然按规范简化计算是满足要求的，但实际上却存在一定的安全隐患。

为安全考虑将立杆纵向间距调整为120 cm，采用相同方法进行有限元计算的横向预应力张拉后立杆的最大承载力需求为Ne2=81.1 kN< [N]=94.2 kN，如图5 (b)所示，满足要求。

图5 预应力张拉前后支架立杆轴力

3 考虑横向预应力张拉耦合效应的模架受力简化计算

采用满堂支架进行预应力混凝土箱梁现浇施工是工程领域较为普遍的施工方案，应用范围非常广。虽然施工现场工程技术人员对预应力张拉引起的模架耦合效应有一定的认识，但满堂支撑架构件数量庞大、杆件约束复杂，并需要繁杂的进行纵横向不均匀分布荷载的数据处理[7]，让其建立接触非线性有限元模型进行分析还有一定的难度，因此提出既能较为准确地考虑模架耦合效应，又便于一线施工技术人员接受的简化计算方法非常必要。

简化计算方法利用结构力学基本原理，取纵向1榀支架立杆为计算单元，将现浇支架和预应力混凝土箱梁简化为平面结构，用梁单元模拟支架和箱梁截面，箱梁简化为闭口超静定结构，将预应力作为外荷载，并考虑预应力的偏心效应，利用结构力学求解器来计算结构的位移和内力响应。由于常规箱梁多为横向对称截面，故只建立一半箱梁和支架模型即可：将预应力作为外荷载，结构自重和施工荷载等简化为竖向外荷载，施加到对应位置的梁单元上，如图6所示。需要注意的是，因张拉过程导致自重分布和结构体系不断变化，严格的计算分析较难实现，在混凝土硬化前，假定支撑系统内力按硬化后的自重分布计算，从而形成统一的结构体系计算。

图6 模架简化计算模型

简化模型计算主要步骤如下：

(1)建立完整的箱梁横截面CAD模型，用于确定具体参数尺寸。

(2)划分单元，根据CAD模型对箱梁顶板、底板、斜腹板进行单元划分，求出各段单元的截面特性。

(3)建立箱梁和支架的杆系模型，根据CAD划分的截面中心位置建点、连线、赋予截面特性，施加边界条件。

(4)施加自重和预应力荷载，求解结构内力和变形。

(5)修改模型，去除受拉的立杆。

(6)重复步骤(4)～步骤(5)直至没有受拉立杆为止，求出最大立杆受力。

为了验证该简化计算方法的准确性和适用性，以依托工程为例，对不同支架高度情况下简化计算结果与有限元计算结果进行对比，结果如图7所示。由此可知：

(1)简化计算方式可以较好地反映预应力张拉引起的耦合效应，不论是张拉前还是张拉后，采用简

图7 结算结果对比分析

化计算出的立杆轴力都与考虑接触非线性有限元的结果比较接近。

(2)在支架高度越矮、竖向刚度越大的情况下，预应力张拉效果越明显，简化计算与有限元分析结果吻合度越好。

4 结论

以保定乐凯大街转体桥工程超宽预应力混凝土W型薄壁箱梁现浇施工支架为例，进行了支架设计验算，并建立接触有限元模型分析了预应力张拉引起的模架耦合效应及其对支架受力的影响，在此基础上提出了考虑预应力张拉耦合效应的支架受力简化计算方法。研究结论如下：

(1)对于支架现浇超宽大预应力混凝土梁，预应力张拉引起的支架内力重分配现象比较明显，支架高度越矮耦合效应越明显，应引起足够重视。

(2)本文提出的考虑预应力张拉耦合效应的简化计算方法能够较为准确地计算出预应力张拉后满堂支架立杆的实际受力情况，计算思路清晰，过程简单，具有较好的工程实用性。