基于和声搜索算法的分散式风场无功优化方法研究

王香香，慕 腾

（1.国网蒙东供电服务监管与支持中心，内蒙古 通辽 028000；2.内蒙古电力科学研究院，内蒙古 呼和浩特 010020）

0 引言

能源短缺、环境污染等问题驱使清洁可再生能源发电技术迅猛发展，对配电网提出了接纳清洁能源发电的新要求，分散式风电作为分布式可再生能源发电的一个重要组成部分和表现形式，将得到前所未有的发展。分散式风电接入配电网，为风电的消纳提供了很好的途径，同时提高了传统电网运行经济性，靠近负荷侧一定量的风电接入，既可避免远距离输电所带来的电能损耗，也可以避免电网输电线路的潮流压力［1-2］。分散式风电开发虽为风电的消纳提供了很好的解决途径，但是随着其在配电网中渗透率的提高，风速随机性、波动性引发的分散式风电出力波动以及风电机组自身特性将给配电网电压稳定［3-5］、网络损耗［6-8］以及继电保护［9-10］造成影响，威胁配电网的安全稳定运行。因此，研究分散式风电接入配电网后如何保证配电网的安全稳定运行，建立分散式风电优化运行模型具有重要的基础意义和应用价值。

研究分散式风电接入配电网的无功电压问题，建立了以经济性、安全性为优化目标的无功优化模型，并提出解决多目标权重系数易受主观臆断的层次分析法，引入求解条件的处理方面更宽松、适用性广的智能算法进行求解，通过在IEEE33 节点系统中的求解测试，对所述的策略的正确性验证，同时与不同智能算法相对比，验证其有效性。

1 含分散式风场的配电网无功优化数学模型

1.1 无功优化目标函数的建立

配电网无功优化对配电系统的经济性、安全性有着至关重要的作用，也是提高经济效益与电能质量的必要手段之一。首先定义经济性目标，即配电网的网络损耗最低值为

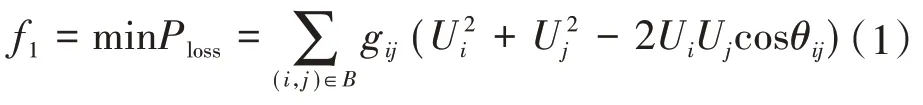
式中：ΔPloss为有功网损；B为网络支路集合；i、j分别为节点编号；θij为节点i、j电压的相角差；gij为支路i-j的电导。Ui、Uj分别为节点i、j电压幅值。

节点电压幅值是对系统安全性的关键因素之一，电压偏差过大会对用户的正常运行，同时危害系统安全。定义安全性目标为

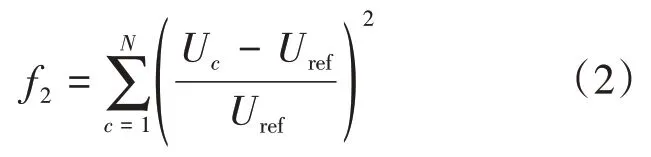
式中：N为场群内各单场个数；Uc为并网点电压；Uref为目标电压值。

根据式（1）和式（2）建立考虑分散式风场经济性与安全性的两个优化运行子目标函数，采取层次分析法（Analytic Hierarchy Process，AHP）来获得权重，使得两个目标的优化运行模型转化为单目标优化模型为

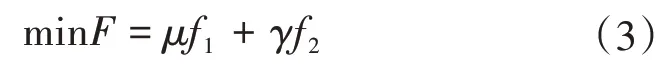
式中：μ、γ为权重系数，且μ+γ=1。

1.2 目标权重系数的确定方法

针对优化模型中两个目标的权重系数选取问题［11-12］，利用AHP来确定权重，增强优化运行的鲁棒性。

首先，比较两个目标函数的相对重要性，根据判断准则生成判断矩阵An×n。判断准则如表1所示。

表1 重要性判断准则

根据生成的矩阵A计算权重，首先计算A矩阵各行因素的乘积Vr为

得出Vr的n次方根Mr，并对其进行归一化，得

则ω=[ω1，ω2，...，ωn]T为所求权重系数。

1.3 无功优化的约束条件

1）潮流方程约束［13-14］为

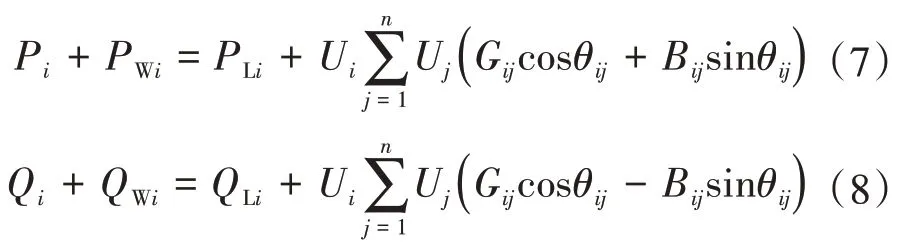
式中：Pi、Qi分别为节点i处系统的有功出力和无功出力；Pwi、Qwi分别为节点i处风机的有功出力和无功出力；PLi、QLi分别为节点i处有功与无功负荷；Gij、Bij、θij分别为支路i-j的电导、电纳以及相角差。

2）线路传输功率约束。从线路功率的角度考虑，线路上的有功功率还应满足输电线路的传输功率极限约束。

式中：Pline.max为配电网线路传输功率的最大值。

3）风机无功出力约束。第x个风电场无功出力为无功补偿设备出力约束Qt与风机的无功功率约束Qwx的约束条件为：

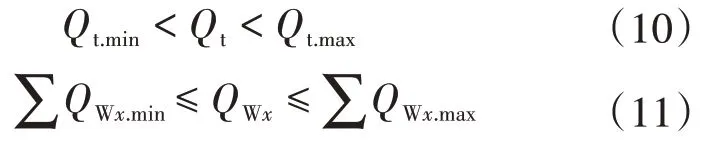
式中：Qwx.max、Qwx.min分别为第x个分散式风电发出的无功功率的上、下限；Qt.max、Qt.min分别为无功补偿设备无功出力的上、下限。

2 求解算法分析与介绍应用

上述模型包含两个目标，属于多目标中非线性规划问题，其中决策变量与约束条件较多，优化运行模型在一个优化周期内进行优化。智能算法对求解条件的处理更宽松、适用性广，被广泛使用［6］。

和声搜索算法（Harmony Search Algorithm，HSA）的主要思路来自音乐表演过程，音乐家根据和音的调节与不断的判断比较来使演奏更加完美。音乐家分别在和声记忆库（Harmony Memory，HM）中选择和声通过相应局部扰动与微调后进行使用。音乐家采用不同方法创作得出新和声且演奏出优美声乐，再通过音乐经验来判断出音乐效果是否好于中最差一个和声，并替换删除旧和声［15-16］。

首先判断出和声库的范围即大小Hms，在HM中，随机生成Hms个初始变量。在HM 中根据选择概率、局部扰动等规则产生新解，并代入目标函数进行求解，同时判断产生的新解是否优于HM 中的最差解，从而来决定是否取代最差解，若未取代，则一直重复之前步骤直到满足其停止要求。

HM的初始化规则为

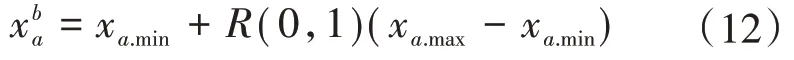
所生成的记忆库为：

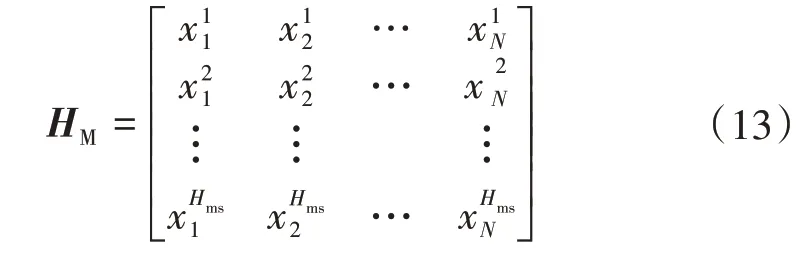
根据记忆库搜索、局部扰动和随机选择3 个规则产生新的和声。具体规则为

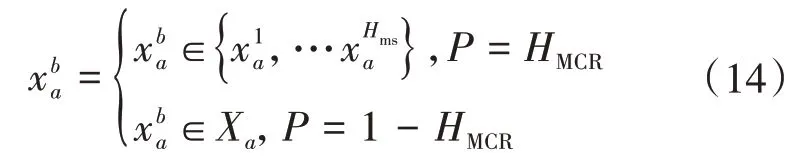
式中：Xi为HM外变量的可行域；P为随机概率；HMCR为和声记忆库保留率。

变量新生成后进行判断是否需要局部微调，若需要，调整规则为

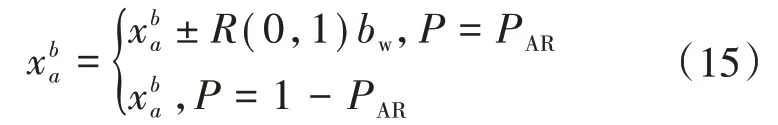
式中：bw为频带宽度；PAR为音高调整率。

上述两种微调方法均是尽可能避免算法陷入局部最优，采用和声搜索算法计算分散式风场无功优化模型。求解流程如图1所示。

具体流程为：

1）初始化配电网参数、风电场运行数据、和声记忆库数量Hms、和声记忆库保留率HMCR、频带宽度bw、音高调整率PAR和创作次数NI等算法参数。

2）形成新的和声向量。

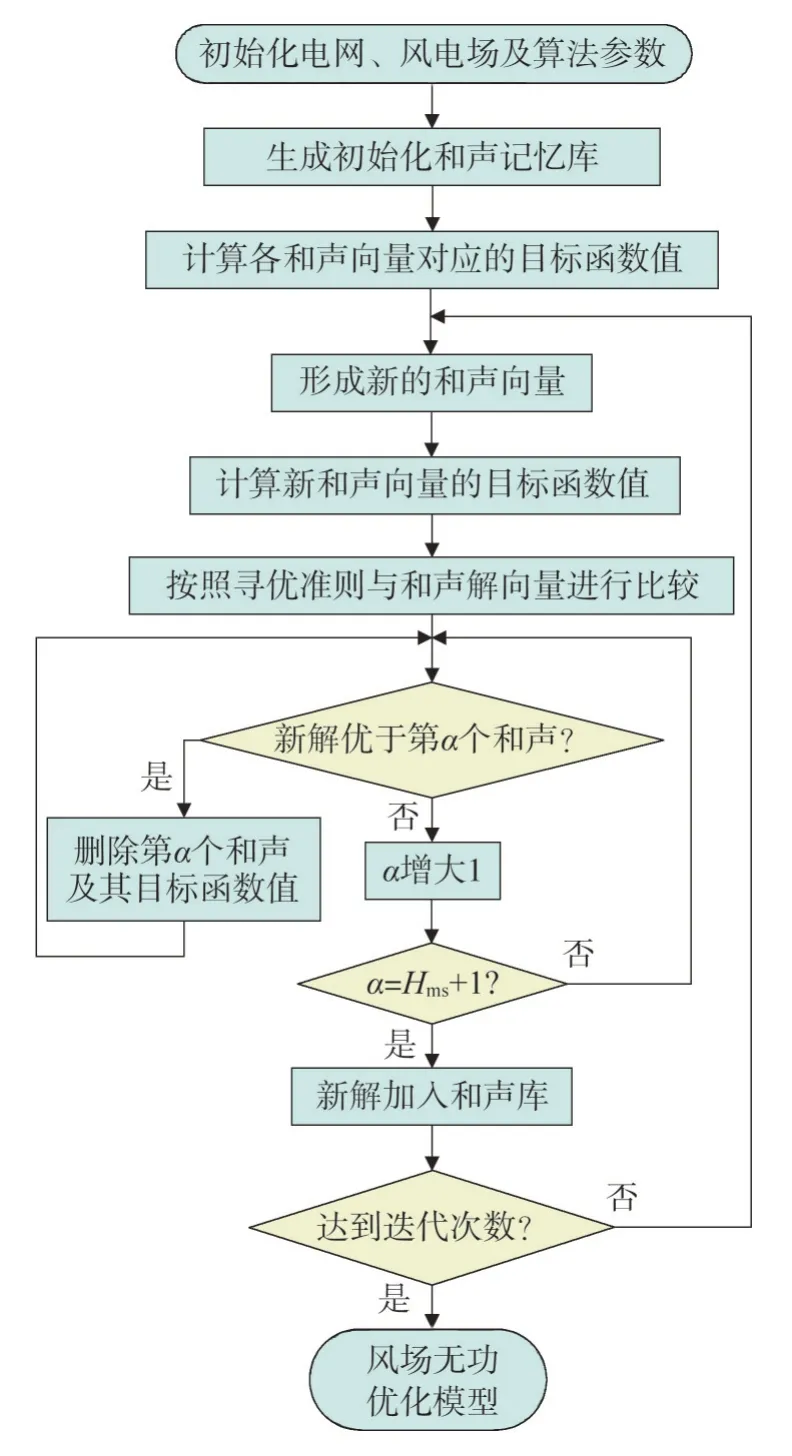
图1 利用和声算法求解无功优化模型流程

3）通过和声记忆库保留率、微调扰动和随机选择来生成新的满足约束的新和声元素，同时求出其和声的目标值。

4）若新生成的和声元素优于HM中若干个和声元素，则删除库中劣质解所对应的满意度，由新元素代替。反之，将新和声删除。

5）替换完成后，判断系统各节点电压、网络损耗是否满足范围，若满足，则输出控制结果；若不合格，重复上述步骤直至达到迭代次数。

3 算例验证

3.1 仿真模型及其基础数据

采用IEEE33 节点配电系统来测试无功优化模型的有效性，具体网架结构如图2 所示。参照文献［17］对风电场无功规划结果，分别在各节点接入相关风机与电容器组，具体参数如表2 所示。其中，和声算法的参数设置为：和声记忆库的大小Hms=10，和声记忆库保留率HMCR=0.85，音高调整率PAR=0.6，频带宽度bw=0.01，迭代次数取1 000。

图2 改进IEEE33节点配电系统

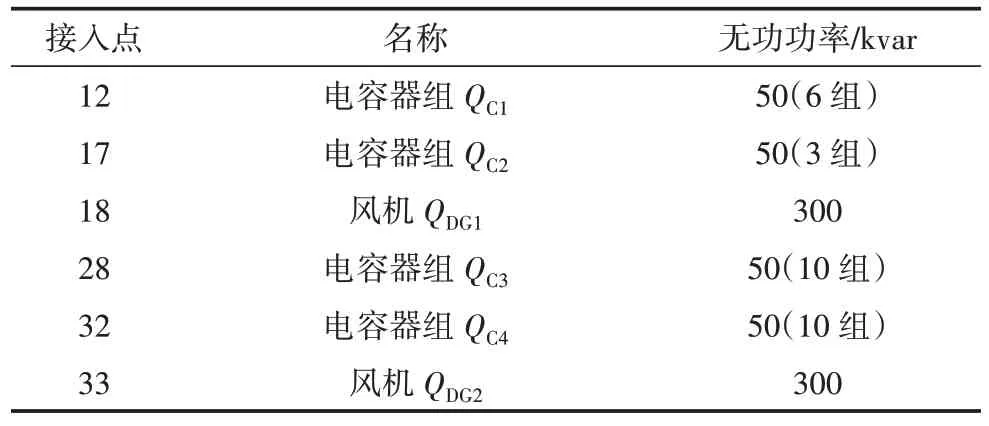
表2 无功优化装置配置

将风电场无功功率调节能力范围以风电场实时有功功率在功率因数为0.95 时对应的无功能力为限。两台风机出力与负荷曲线如图3和图4所示，其中两台风机出力情况一致。

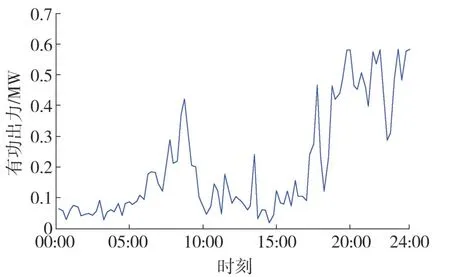
图3 两台风机出力变化曲线

图4 典型日负荷变化曲线

3.2 无功优化结果分析

首先考虑发挥风机自身无功能力，在满足连续运行的约束条件下，进行前后优化比较。采用HSA与粒子群算法（Particle Swarm Optimization，PSO）对IEEE33 节点配电系统所接风场与电容器组进行优化计算，其中，PSO 的对应参数如：种群规模，迭代似乎以及权重系统均与和声算法一致。优化结果如表3所示。

表3 不同算法优化效果分析

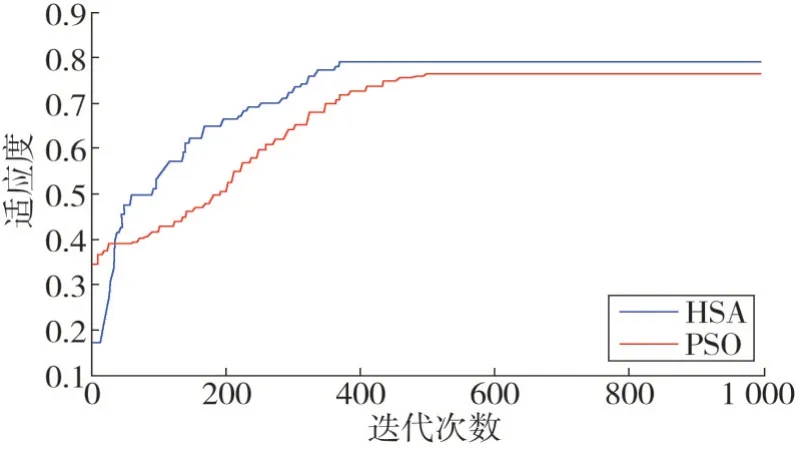
图5 迭代收敛过程

由表3 可知，两种算法均可实现风机自身无功能力的充分利用，并且网络损耗从192.7 kW 分别降低至130.5 kW、110.9 kW。同时，相较于网损或者如图5所示迭代收敛速度两方面，HSA均优于PSO。

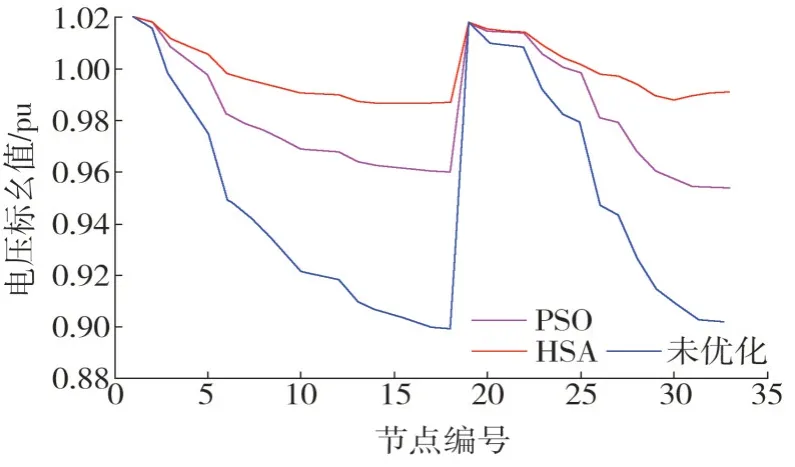
图6 不同运行方式下电压分布

由图6 可知，优化前系统整体电压水平较低，个别节点电压甚至低于0.9 pu，优化后，各节点电压均恢复至0.95 pu 以上，电压水平合理。综上所述，所建立的无功优化模型在改善节点电压与提升经济效益方面效果明显，并且所采用的和声搜索算法在求解多目标问题中更能满足电网需求与发展。

4 结语

对含分散式风场的无功优化问题进行了研究，以配电系统各节点电压合格、经济性为目标，构建了含分散式风场无功优化数学模型。考虑双馈风机自身的无功输出能力的前提下，利用和声算法与粒子群算法进行分别求解无功模型，最后在IEEE33 配电系统进行数据测试。仿真结果表明，所采用的无功优化控制策略可以提高电压质量，同时兼顾经济性，同时，和声搜索算法相比于传统的粒子群算法可以更快收敛，得到较优于粒子群算法的解，验证了所研究和声搜索算法的正确性和有效性。