基于机器学习技术的蒸发皿蒸发量估算模型
2021-05-19龙亚星黄勤李成伟
龙亚星 黄勤 李成伟
(1 陕西省大气探测技术保障中心,西安 710015; 2 秦岭和黄土高原生态环境气象重点实验室,西安 710016; 3 陕西省气象信息中心,西安 710015)
引言
机器学习是人工智能研究领域中一个极其重要的研究方向,在当下的大数据时代背景下,捕获数据并从中发现有价值的信息或模式,成为气象行业创新综合观测、预报预测和气象服务方式的重要手段[1-2]。基于气象观测数据,机器学习技术在农业用水调度、空气质量预测、天气雷达超折射回波识别等社会生产生活领域中得到了广泛应用[3-5]。蒸发是水循环的重要环节,是自然界物质能量循环代谢的主要手段,通过蒸发将植物、土壤、大气和水分紧密的联系在一起,其在全球气候变化研究中具有敏感的指示作用[6-10]。
有研究表明,西北干旱区蒸发潜力在1993年出现了一个明显的转折变化,由显著下降逆转为显著上升的趋势,气候变暖、蒸发水平增大对西北干旱区生态效应的负作用已日趋凸显[11]。于占江等[12]分析近40年京津冀蒸发皿蒸发量与影响因子的相关系数发现,气温日较差、日照时数和平均风速是影响京津冀地区蒸发皿蒸发量变化的主要因子,在平原地区,平均风速是主导因子;在山区和高原地区,日照时数是主导因子。申双和等[13]利用中国472个气象站1957—2001年20 cm口径蒸发皿的实测资料分析了中国小型蒸发皿蒸发量的变化趋势及其变化原因,结果表明:尽管在这45年间中国年平均气温以0.2 ℃/10a的趋势递增,但是蒸发皿蒸发量总体上却以-34.12 mm/10a的速度递减;通过对彭曼公式中能量平衡项和空气动力项的分析表明,东部蒸发皿蒸发量的下降主要是因为供蒸发的能量显著减少,而西部地区蒸发皿蒸发量的下降主要是供蒸发的动力下降所致;对各气象因子的趋势分析和相关分析表明,影响蒸发量的主要因子为风速和日照时数。陕西位于中国西北内陆东部,以北山和秦岭为界,从北到南为温带干旱性气候、暖温带湿润性气候和亚热带大陆性气候3个气候带,形成陕北黄土高原、关中平原和陕南秦巴山地,地貌多样,具有多种农牧业生产方式,用水矛盾突出,生态环境问题是该区域的重要问题[14-16]。
全国地面气象观测自动化改革后,小型蒸发皿人工观测任务全部取消,涉及全国2 000余个国家级气象观测站。如何弥补国家基准气候站、基本气象观测站冬季结冰期以及(常规)气象观测站蒸发皿蒸发量观测资料的空缺,是一个值得研究的科学问题。吴华斌等[17]利用地面气象观测资料,探讨了日蒸发量与其他气象因子的相关性,建立了基于多元线性回归的日蒸发量估算方程,年蒸发量估算值与实测值的平均相对误差达到17.2%,估算绝对误差在[-1.0,1.0]区间的比例达到83.2%。徐俊增等[18]建立了基于气象预报的参考作物蒸发蒸腾量的神经网络预测模型,平均相对误差达到17.9%,相对误差在20%范围内的合格率为76.0%。闵骞[19]以彭曼公式为基础,根据中长期气候预报中一般可给出的月、旬平均气温和中雨(雪)以上降水天数,对彭曼公式进行分解,通过分别建立月、旬水面辐射平衡值R、空气干燥力Ea2个参数的预测模式,建立月、旬水面蒸发量预测模型,月、旬水面蒸发量的预测平均相对误差分别达到11.9%、11.2%,相对误差在20%以内的合格率分别为70.4%、72.2%。以上建立的估算或预测模型均达到了生产上的一般精度要求,但部分指标值如平均相对误差、绝对误差等还存在提升的空间,且彭曼公式虽然可应用于蒸发皿蒸发量估算,但原公式中的水面辐射平衡值R和空气干燥力Ea参数还需要根据区域气候特征进行本地化修正,计算过程复杂。本文旨在利用常规地面气象观测资料,研究基于机器学习技术的不同气候区域、不同时间尺度的蒸发皿蒸发量估算方法,同时探索基于机器学习技术的日蒸发量数据质量控制内部一致性检查方法[20]。
1 资料与方法
1.1 资料来源
本文选取陕西省15个国家基准(基本)气象站2004—2015年的逐日地面气象观测数据,数据均通过CIMISS气象数据统一服务接口获取,资料站点分布见图1。

图1 陕西省15个国家基准(基本)气象站分布
各气象站蒸发皿蒸发量在结冰期由314 cm2表面积、约10 cm高的小型蒸发皿观测,其余时间由表面积3000 cm2、深度60 cm的E-601B大型蒸发皿测得。2种蒸发皿的主要性能参数见表1。

表1 小型蒸发皿与E-601B大型蒸发皿主要性能参数及观测资料精度
影响蒸发的主要气象因子为动力因子、热力因子和水分因子[21],因此选择逐日平均气压、平均气温、日照时数等15个气象要素作为影响蒸发(响应变量)的特征变量,某一日的特征变量及响应变量构成1个实例。为避免资料插补带来的误差影响,对于特征变量或响应变量存在缺测或数据错误的实例,不纳入数据集。同时,由于区别表面有无自由水存在的状况非常有必要,因此需要考虑水量、水的状态;且在干燥和半干燥地区,有必要区别蒸发面的大小及形状,因此将小型蒸发皿蒸发量折算为大型蒸发皿E-601B蒸发量,折算系数τ取陕西省年平均值0.62[22-25]。本文估算及检验的蒸发皿蒸发量与大型蒸发皿蒸发量对应。
分别建立陕北、关中和陕南3个区域数据集,以及分别属于陕北、关中和陕南的榆林、泾河和汉中3个单站数据集。每1个数据集包括训练集、验证集和测试集,训练集用于训练和构建模型,验证集用于参数优化及模型的选择,测试集用于对最终选择的模型进行检验评估。各区域、单站2005—2014年日资料中,75%的实例被随机地划分为训练集,其余25%的实例作为验证集。数据集基本情况见表2。

表2 区域及单站数据集基本情况
利用SPSS软件分别对各数据集2005—2014年数据进行分析,得出年尺度下蒸发皿蒸发与各气象要素的Pearson相关系数(表3),可以看出,同一类别的气象要素中,平均量一般不是最大的影响因子;平均气压、最高气压和最低气压对陕北、关中和陕南各区域整体和区域内代表性站点的影响程度存在较大差异,说明进行区域或单站蒸发量估算时需要考虑的主要气象因子及其权重系数不同。
1.2 资料标准化
在机器学习中,为便于训练和更好地反映各特征变量与响应变量之间的相关关系,对表3中的所有特征变量数据进行标准化,处理方法如下:
(1)


表3 年尺度下蒸发皿蒸发与各气象要素的Pearson相关系数
1.3 评价指标
本文机器学习模型的评价指标包括:均方误差MSE(Mean Square Error,MSE)、总相对误差TRE(Total Relative Error,TRE)、准确率CR(Correct Rate,CR)以及决定系数R2,评价估算值偏离实际观测值的程度和估算准确率,MSE为损失度量指标[26]。
(2)
(3)
(4)
(5)

2 估算模型
2.1 回归方法
根据日平均气压、平均气温等进行蒸发皿蒸发量估算,属于监督学习中的回归问题,学习的目标是选择损失最小的模型。本文采用的回归方法为k近邻法(KNN)、多层感知机(MLP)。KNN回归的主要算法如下:给定1个训练数据集,在训练数据集中找到与测试数据集中实例最邻近的k个实例,然后将这k个邻居的平均值作为该测试实例的估算值。本文中,KNN回归方法优化的参数为:k值(n_neighbors=k),由于数据集已进行标准化,本文距离度量采用欧式距离。
MLP又称为前馈人工神经网络,是一种广义的线性模型,除了输入、输出层,其中间可以有多个隐层,层与层之间为全连接,执行多层处理后得到结论。在MLP中,多次重复计算线性回归估算模型中加权求和的过程,并计算代表中间过程的隐单元,然后再计算这些隐单元的加权求和并得到最终结果。本文中,MLP回归方法优化的参数为:隐层数量(hidden_layer_sizes)、迭代次数(max_iter)。
2.2 初始模型
基于陕北、关中和陕南训练集及验证集,分别利用KNN(n_neighbors=5)、MLP(hidden_layer_sizes=100,max_iter=200)2种回归方法及其默认参数建立区域估算模型,模型在验证集上的指标值如表4所示。
从表4可以看出,除关中及陕南的TRE指标外,MLP模型各指标均优于KNN模型:MSE平均约低0.1、R2约高3%、CR约高4%。KNN、MLP回归模型的总相对误差TRE均在2%以内,但不同气候区域的R2指标性能差异较明显,均呈现以下特点:陕北>关中>陕南,级差平均约为4%。

表4 KNN、MLP模型在默认参数时的估算指标值
2.3 参数优化
为确保KNN、MLP模型具有最优泛化性能,利用S折交叉验证(S-fold cross validation)、管道(Pipe)和网格搜索技术(GridSearch),根据各模型R2指标性能和时间复杂性选择最优模型参数[26,29]。基于陕北、关中、陕南训练集及验证集的KNN模型不同k值(k∈[1,100])的R2曲线、MLP模型不同隐层数量及迭代次数的R2热图如图2所示。
从图2可以看出,各回归方法在默认参数条件下均未达到R2最优估算性能,但部分达到次优。图2a表明,KNN模型在不同区域的最优参数(即k值)基本接近:n_neighbors=20,默认值n_neighbors=5与其相差较大;图2b表明,陕北MLP模型的最优参数为:hidden_layer_sizes=10, max_iter=1 000,其在默认参数时的R2值较低,且可以看出,陕北MLP模型对参数较为敏感;从图2c、d看出,关中、陕南MLP模型的最优参数均为:hidden_layer_sizes=(5,12) ,max_iter=200,且默认参数为其次优参数。
2.4 估算模型检验
2.4.1 区域蒸发量估算
基于以上构建的区域估算模型及最优参数,利用2015年陕北、关中和陕南各区域测试集分别检验区域估算模型的应用效果,估算值与观测值的散点图及其拟合曲线以及评价指标值、估算值绝对误差分布等如图3所示。
从图3a、b、c可以看出,陕北KNN模型在测试集上具有良好的泛化性能,且各指标均优于MLP模型;MLP模型泛化性能较差:MSE、TRE分别达到3.16、20.4%,而R2、CR分别仅为0.459、27.8%,估算值绝对误差在[-1.0,1.0]区间的比例仅为55.4%。从图3d、e、f可以看出,关中MLP模型的MSE、R2和CR指标均略优于KNN模型,TRE指标相对较劣,KNN、MLP模型估算值绝对误差在[-1.0,1.0]区间的比例分别为86.3%、89.8%。从图3g、h、i可知,KNN、MLP模型在陕南的估算值指标性能基本接近,其绝对误差在[-1.0,1.0]区间的比例分别为92.2%、94.4%。KNN、MLP模型在关中、陕南均具有良好的泛化性能。
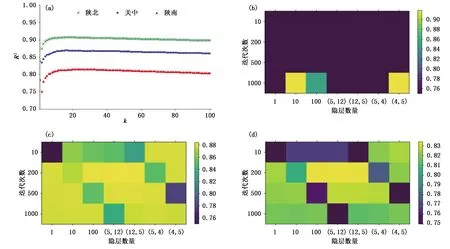
图2 回归模型不同参数在验证集上的R2值: (a)KNN模型R2曲线,(b)陕北MLP模型R2热图,(c)关中MLP模型R2热图,(d)陕南MLP模型R2热图

图3 2015年陕北、关中、陕南蒸发量估算值与观测值散点,评价指标值与估算值绝对误差
2.4.2 单站蒸发量估算
由于KNN模型在陕北、关中和陕南蒸发量估算过程中均表现出良好的泛化性能,因此分别利用KNN区域估算模型及其最优参数(n_neighbors=20),对各区域的代表性站点即榆林、泾河和汉中的2015年蒸发量进行估算。同时,基于榆林、泾河和汉中2005—2014年观测数据,分别建立各站点的KNN单站估算模型及其最优参数(榆林:n_neighbors=15,泾河、汉中:n_neighbors=25),对各站点2015年蒸发量进行估算。基于区域估算模型、单站估算模型的单站蒸发量估算值与观测值的散点图及其拟合曲线以及评价指标值、估算值绝对误差分布如图4所示。
从图4可以看出,基于单站估算模型的单站蒸发量估算指标性能均优于基于区域估算模型的单站蒸发量估算指标性能:榆林CR偏高9.9%,TRE偏低5.6%,区域估算模型的TRE值达到-7.1%,区域、单站模型估算值绝对误差在[-1.0,1.0]区间的比例分别为:84.7%、83.8%;泾河MSE偏低0.21,CR偏高4.3%,TRE偏低10.5%,区域估算模型的TRE值达到-12.7%,区域、单站模型估算值绝对误差在[-1.0,1.0]区间的比例分别为:78.4%、79.6%;汉中MSE偏低0.11,CR偏高8.2%,TRE偏低0.8%,区域、单站模型的TRE值均相对较高,分别达11.1%、10.3%,区域、单站模型估算绝对误差在[-1.0,1.0]区间的比例分别为:88.9%、94.2%。同时可以看出,榆林、泾河单站模型估算值绝对误差分布在0.0 mm时对应的实例数约为200,而汉中对应的实例数约为100,这可能与各单站模型的鲁棒性以及陕北、关中和陕南各区域天气、气候特征有关。

图4 2015年榆林、泾河、汉中蒸发量估算值与观测值散点,评价指标值与估算值绝对误差
3 结论与讨论
本文在建立陕北、关中和陕南区域数据集以及榆林、泾河和汉中单站数据集的基础上,分析了气温、地温和日照等气象要素与蒸发皿蒸发的相关性,通过优化模型参数,分别建立了蒸发量区域估算模型、单站估算模型,得出如下结论:
(1)年尺度下,影响陕北、关中和陕南各区域以及各区域代表性站点榆林、泾河和汉中蒸发皿蒸发量变化的主要因子存在差异,且同一类别气象要素中,平均量一般不是最大的影响因子;平均气压、最高气压和最低气压对陕北、关中和陕南各区域整体影响较小,但对各单站的影响较大。
(2)KNN、MLP估算模型在默认参数条件下均未达到最优R2估算性能,KNN模型在不同区域的最优k值基本接近(n_neighbors =20),但默认值(n_neighbors =5)与其差距较大,陕北MLP模型对参数选择较为敏感,关中、陕南MLP模型的最优参数相同,且默认参数为其次优参数。
(3)进行区域蒸发量估算时,KNN模型表现出良好的泛化估算性能,其MSE、TRE和CR指标值平均分别为0.42、2.1%、57.0%;陕北MLP模型的泛化性能较差,MSE、TRE和CR指标值分别为3.16、20.4%、27.8%;关中MLP模型的MSE、CR指标略优于KNN模型,TRE指标则相比较劣;陕南KNN、MLP模型指标性能基本接近。
(4)进行单站蒸发量估算时,基于k近邻法的KNN单站估算模型性能优于区域估算模型,MSE、CR指标值平均为0.48、55.0%,榆林与泾河TRE指标绝对值平均为1.6%,汉中TRE指标值偏高,达到10.3%。
以上研究结论及其与文献[17-19]的评价指标简单对比表明,本文建立的蒸发皿蒸发量估算模型部分评价指标表现良好,可以为陕西省不同气候区域及单站、不同时间尺度的蒸发量估算以及日蒸发量数据质量控制提供一种基于机器学习的方法。但是本文也存在一些问题,如未对其他估算或预测模型如彭曼公式进行本地化参数修正、验证以及与本文建立的估算模型进行基于同一数据集的检验与对比分析,也未对MLP模型应用于陕北蒸发量估算时泛化性能较差、汉中单站蒸发量估算时TRE指标值偏高的原因进行分析。因此,下一步将对影响蒸发皿蒸发变化的主要气象因子在不同气候区域及单站、不同时间尺度上的变化特征进行研究,并对比不同模型在同一数据集上的检验效果。
