辽东湾海岸侵蚀监测点控制网优化设计与实现

2021-05-19周玉洁

辽宁自然资源 2021年3期

周玉洁

（兴城市自然资源事务服务中心，辽宁葫芦岛 125100）

受国家海洋环境监测中心委托，对辽东湾海岸侵蚀监测点进行控制测量工作。测区位于绥中至兴城沿海一带，西起绥中万家止锚湾，东至兴城海滨乡，共布设15个监测点，埋设标石，东西距离75千米。

为减轻测量劳动强度，提高工作效率，本次项目拟采用GPS方法布设控制网，以GPS拟合高程代替水准高程。然而，GPS 直接测量的高程成果为GPS大地高，大地高只是一个几何量，不具有物理意义。正高是一种唯一确定的数值，可以用来表示地面的高程[1]，但是正高又不能精确的求定，我们实际工程中应用的是以似大地水准面为起算面正常高[2]，本次项目打算用两种方法分别拟合似大地水准面，然后选取最优模型，进行似大地水准面的优化，先将GPS测得的大地高转为1956年黄海高程系，再由1956年黄海高程系加常数转为1985国家高程基准。

一、概述

据2012年重点岸段海岸侵蚀监测显示，我国砂质海岸和粉砂淤泥质海岸侵蚀严重，侵蚀范围扩大，局部地区侵蚀速度呈加大趋势。辽东湾绥中海岸侵蚀给当地人民的生产和生活带来严重危害，因面临海岸侵蚀的较高危险性促使绥中沿海地区海岸侵蚀灾害危险性研究备受关注。海平面上升造成大部分地区呈现明显的强侵蚀和严重侵蚀状态（图1）。因此，基于未来海平面上升导致的海岸侵蚀危险度预测对海岸侵蚀研究有重要意义。

二、研究的主要内容

测区东西长75km，共布设14个控制点（原本布设15个控制点，其中25号桩被破坏），测区内可利用的控制点6个，控制点平面坐标成果为1980西安大地坐标系统、高程系统为1956年黄海高程系统，1985国家高程基准高程控制点个数不足，不能满足要求提供的1985国家高程基准要求，测区内只有其中两个控制点同时拥有1985国家高程基准高程，需要进行高程系统转换才能达到成果要求。故着重解决项目中遇到的GPS控制网优化设计、GPS高程拟合、不同高程系统间的转化问题。

三、GPS控制网的设计

1.GPS控制网基准选择

起算点平面坐标采用1980西安坐标系，高程系统采用1956年黄海高程系统整体平差，再转换至1985国家高程基准。GPS基线向量为WGS-84坐标系，时间系统采用北京时间，中央子午线经度为120°，测区位于高斯3度投影带第40带。

2.GPS网形设计

已知控制点6个，待测点14个，GPS接收机3台，测绘人员4人，结合仪器设备、人员、时间、成本等实际情况，宜采用边连接布网形式，观测18个时段，每时段观测120分钟，总基线54条（图2）。

3.GPS控制点优化

根据测区已有控制点成果，外业实地踏勘，发现已有资料的6个控制点均保存完好，表面上未遭到破坏。但在实际中发现，无约束平差时，基线向量解算合格；约束平差时，当6个控制点全部参加解算时，基线向量解算不合格。初步怀疑某个控制点可能有问题，故采用分析试验法进行控制点完好性检验。

图1 2012年绥中县砂质海岸侵蚀状况

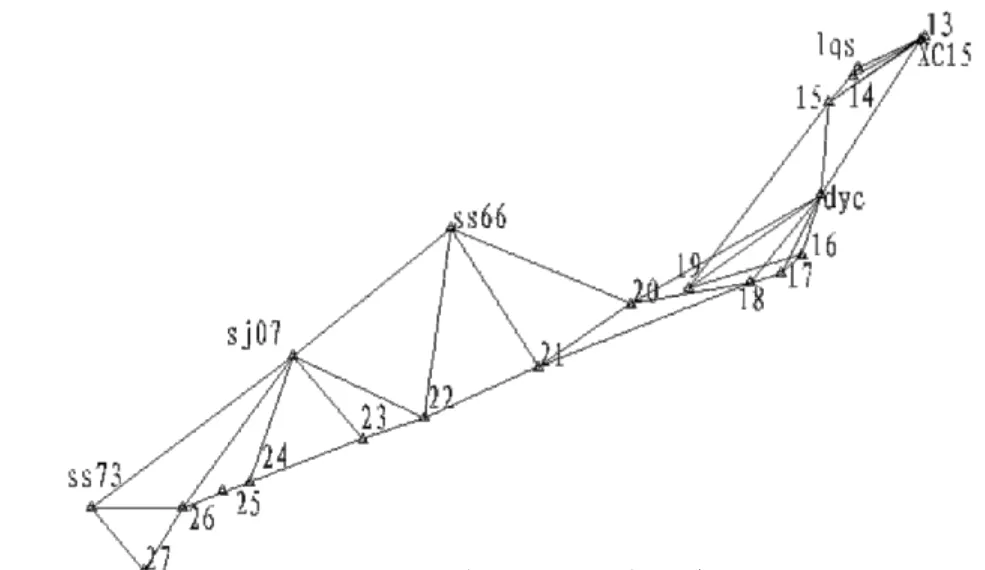
图2 2012年绥中县砂质海岸侵蚀状况

基本设计思路是：先选取相对稳定的控制点作为起算点，对解算成果进行分析，初步掌握可能存在问题的控制点；再选取解算精度较好的控制点作为起算点，对解算成果进行分析；经过几次分析后，最终确定有问题的控制点，再通过三等水准测量求得该点的水准高程。

4.平差处理

为全面考察GPS网的内部符合精度，首先进行无约束平差，以符合各项质量检验要求图的独立基线组成的闭合图形和三维基线向量及其相应的方差协方差阵作为观测信息，进行GPS网的无约束平差。

无约束平差处理后，进行约束平差，首先选取约束平差控制点，根据需要选择了xc15，lqs，dyc，ss66，sj07和ss73等6个控制点作为起算点，进行约束网平差。

四、GPS高程拟合

GPS高程拟合的基本思路就是在小区域的GPS网中，用水准测量的方法联测网中若干GPS点的正常高(这些联测点称为公共点)，那么根据各GPS点的大地高就可求得各公共点上的高程异常。然后由公共点的平面坐标和高程异常采用数值拟合计算方法，拟合出区域的似大地水准面，即可求出各点高程异常值，并由此求出各GPS点的正常高[3]。

本次高程拟合主要考虑平面拟合法、二次曲面拟合法。

1.平面拟合法程序设计

为了求得GPS点的正常高，首先需要建立似大地水准面的数学模型。一次曲面的一般形式为：

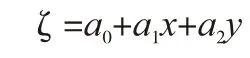
式中ζ表示已知高程异常值，表示已知高程拟合点的平面坐标值，a0，a1，a2为所求参数。根据这个原理，相应的数据模型就能以程序语言的方式表示出来（图3）。

2.二次曲面拟合法程序设计

二次曲面法拟合似大地水准面[4]的基本原理是将高程异常近似地看作一定区域内各点坐标的曲面函数，用已联测水准的GPS点高程异常拟合这一函数，求得函数的拟合系数，进而确定一定区域内高程异常与点平面坐标的函数关系。

二次多项式一般形式为：

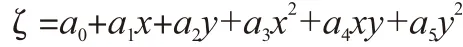
式中ζ表示已知高程异常值，表示已知高程拟合点的平面坐标值，a0，a1，a2，a3，a4，a5为所求参数。但是本项目中仅联测了6个已知控制点，只能采用不完全二次多项式曲面拟合模型，不包括x2和y2两项，共4个系数，可列立6个误差方程式，按最小二乘平差求出二次曲面拟合参数。那么，不完全二次多项式一般形式就变为：

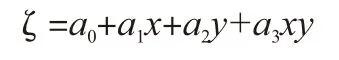
同样，根据此原理，相应数据模型也能以程序语言方式表示出来。

3.精度比较

根据编译好的程序，平面拟合计算后GPS水准拟合内附合精度为39.22mm。二次曲面拟合计算后GPS水准拟合内附合精度为17.52mm。可以看出，二次曲面拟合精度明显高于平面拟合精度，且能满足工程项目施工要求，故本次高程计算结果采用二次曲面拟合（表1）。

表1 拟合残差精度对照表单位：毫米

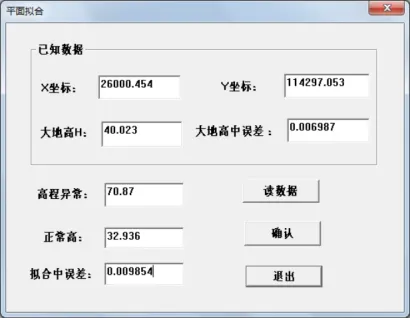
图3 平面拟合程序界面

五、不同国家高程系间的转换

辽东湾测区内搜集的已有控制点资料中，除sj7和dyc点同时具有1956年黄海高程系与1985国家高程基准高程值外，其余各点均只有1956年黄海高程系高程值，仅两个控制点无法通过GPS高程拟合来完成GPS大地高到正常高的转换，只能先将GPS大地高转为1956年黄海高程系下的正常高，再通过sj7和dyc已知的两个高程系下的高程差值，寻求一个加常数改正。