弥散吊顶通风系统气流相互作用原理分析

石盼弟 余 涛 袁艳平

弥散吊顶通风系统气流相互作用原理分析

石盼弟 余 涛 袁艳平

（西南交通大学机械工程学院 成都 610031）

弥散吊顶通风系统是一种利用多孔吊顶板作为末端向房间送风的新型通风方式，可实现低温送风且室内人员区无冷风感。然而，该通风系统中热源羽流与送风射流的相互作用原理缺乏相关研究。采用理论分析和数值模拟相结合的方法，建立了弥散吊顶通风系统的送风射流与热羽流相互作用模型，分析了热羽流与送风气流的相互作用规律。结果表明：热羽流和送风射流会在某个高度强烈混合，混合区域内热羽流浮力作用与送风射流动量相当；相互作用面高度随热源功率的增加而增加，随送风速度的增加而减小；且当热源大小与送风速度一定时，热羽流所受浮力大小几乎不变，作用面高度与送风温度基本无关。本研究可为弥散吊顶通风系统的设计提供理论基础。

弥散吊顶通风；热羽流；送风射流；浮力作用

0 引言

目前，民用建筑中最常见的通风系统是混合通风与置换通风。混合通风利用送风射流的诱导作用，从天花板或侧墙提供高动量空气与室内空气混合，进行热湿交换。置换通风则是将空气以低风速、低紊流度、小温差的方式，直接送入人员活动区的下部，与室内空气混合进行热湿交换。两种通风系统都能达到送风目的，但在高负荷、大风量、低温送风时，两种系统会出现室内热舒适性差、能耗高、噪音等问题[1]。

弥散吊顶通风系统（Diffuse Ceiling Ventilation System, DCV）作为一种新型的气流组织方式，起源于欧洲，最初应用于猪舍[2,3]等大型牲畜建筑物，该通风系统能耗小、投资成本低、可以实现低温送风且室内人员无冷风感、送回风温差大等特点[4,5]，近年来也逐渐应用在办公室、学校等室内负荷较大的建筑中。学者[6,7]对该系统的送风特性、室内热舒适性以及适用性进行了实验和数值模拟分析，但弥散吊顶通风系统下热羽流与送风射流的相互作用过程缺乏深入研究。

本文以弥散吊顶通风系统下室内单点源为研究对象，基于热羽流理论和送风射流理论，利用理论分析和数值模拟相结合的方法，对该通风系统下气流的相互作用过程进行分析。本研究有助于完善弥散吊顶通风系统的现有理论。

1 DCV下热羽流与送风射流相互作用过程

1.1 弥散吊顶通风系统原理

该通风系统由静压室（吊顶与楼板间的空间）、多孔吊顶板、下部房间三部分组成，如图1所示。

图1 弥散吊顶通风系统示意图

DCV首先将新鲜空气供应到静压室内，由于静压室的均压作用，新鲜空气通过多孔吊顶板均匀扩散到下部房间，达到通风降温的目的。该通风系统是以整个多孔吊顶板作为送风末端，风口面积大，新鲜空气以较低速度进入下部房间。利用送风气流的低动量和室内热源的羽流作用，在吊顶下部进行气流混合，人员区无冷风感，故可实现低温送风。

送风射流与热羽流在下部房间内某一平面处发生剧烈混合。把发生气流剧烈混合的面定义为相互作用面，相互作用面所对应的距热源顶部的距离称为相互作用面高度。当该高度大于0时，冷气流无法到达人员区，无冷风感。在作用面处，送风射流的动量变化与热羽流所受到的浮力相等，如式（1）所示：

式中：浮为热羽流所受的浮力大小，N；F为送风射流在作用面高度处的力，N，该力等于送风射流的动量变化量。

1.2 热羽流与送风射流相互作用理论

1.2.1 热羽流理论分析

热羽流是因靠近热源的气体受热而温度升高，密度减小，相对于周围的气体出现局部的密度差而产生浮力的一种常见的对流现象[8]。热羽流分析是以经典的点源理论为基础的，但工程应用中最常遇到的问题是实体热源，即面热源或体热源。目前常用的计算实体热源的方法有三个：虚拟点源法、积分法和数值模拟法。文献中[9]Skistad等人推荐的方法就是虚拟点源法，即真实热源的羽流可以认为是在热源下方某一位置处的虚拟点源的羽流。

本文对热羽流的分析采用的基本假设包括：卷吸假设、相似假设和密度假设。点源浮力羽流中控制流动最主要的参数是浮力通量，可由下式计算[10]：

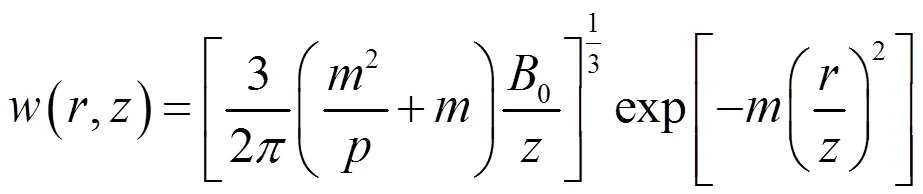
其中，为速度扩散系数，为温度扩散系数。故点源浮力羽流在高程断面上的体积流量为：

为了简化问题与消除空间参数，本文采用高帽分布，而且大量的研究结果表明，高帽分布能较好的描述羽流的运动发展情况。故羽流的轴心速度和折算重力加速度的表达式为：

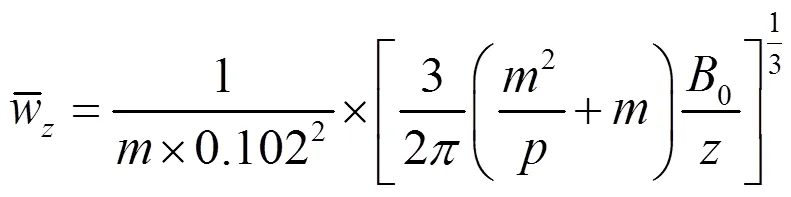
故羽流所受的浮升力为：

式中，，的值根据文献[13,14]取=96，=71进行计算。故由式（2）和式（8）可得出羽流上升过程中所受的浮力大小：

面热源与体热源的羽流量计算一般用到虚拟点源法，此方法的关键就虚拟极点距的确定。根据有关文献，面热源的虚拟极点距z一般是2.3—1.6，则对于直径为的圆形面热源，其浮力羽流量为：

同理，体热源的虚拟极点距可以根据文献[10]提出的经验公式得出：

无限空间自然对流换热的经验公式：

层流：=0.6，=1/5；紊流：=0.17，=1/4。经计算，在模拟的热源大小范围内，Ra最小为1.8×108，显然，热源侧壁流动处于层流状态，所以选用层流公式进行侧面竖壁自然对流边界层厚度的计算。

由上所述，圆柱体热源热羽流的羽流量公式为：

由于面热源与体热源的羽流量公式是利用虚拟点源法，所以面热源与体热源羽流上升过程中所受的浮力大小和点热源热羽流的浮力公式相等。

1.2.2 送风射流的理论分析

通风空调工程中所遇到的气流运动，大都是非等温送风。非等温送风射流是以动量和浮力为原动力进行送风。但由于本次研究中送回风温差太小，所以送风射流的浮力忽略不计，因此仅考虑送风射流Z轴上动量的变化，且本次研究以竖直向上的方向为正方向[16]。

当流体流过固体或者流体时，该流体可能会对流过的固体或者流体产生力的作用。因此对该方向上的送风射流应用动量守恒定理，则送风射流作用在作用面处的力由下列公式计算得出：

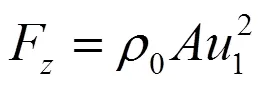
1.2.3 两气流相互作用

依据上述点源热羽流理论和送风射流理论，将式（9）和式（11）代入到式（1）就可以得出DCV下两气流在相互作用面处的理论解式（12）。

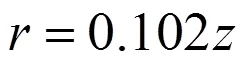
2 结果分析

2.1 单羽流作用的计算方法验证

热羽流作用可采用理论分析、实验与数值模拟的方法进行研究。为验证DCV下单羽流作用的计算方法是否合理，本文拟采用文献[17]中的实验结果与热羽流理论和数值模拟结果进行验证。文献[17]中采用现场实验研究了上下通风口分别设置在地面和屋面处，热源为点热源的单羽流作用过程。以该文献中的测点（=0.4m，=0.4m，=0-1m）处的实验温度与热羽流的理论速度分布为验证依据。面热源与体热源的验证与点热源相同，本文不在赘述，只分析面热源与体热源的气流混合特性。

图3 数值计算模型图

本文采用Fluent软件模拟单点源的热羽流作用，将房间简化成一个1m×1m×1m（L×W×H）正方体，室内热源简化为单独一个点（长方体足够小）源置于地板正中间，模型和热源附近的网格如图3（a）、（b）所示。该热羽流的数值模拟采用Realizable湍流模型，压力项采用Body Force Weighted，气体采用Boussinesq假设，出口为压力出口。

图4 温度和速度分布对比图

图4（a）为测点d处实验温度、模拟温度与理论温度的对比。实验温度与模拟温度分布规律基本相同。理论温度值在0.5m以下的变化趋势不明显，主要是由于本文采用的热羽流理论没有考虑温度分层，而实验和数值模拟结果存在温度分层。

图4（b）是某一高度处理论速度分布与数值模拟速度分布的对比图，热羽流在某一高度处为高斯分布。两种方法得出的结果相对误差均在20%以内。

因此，数值模拟采用上述湍流模型与边界条件是合理的，可用于下一步对热羽流与送风射流相互作用特性的模拟研究。

2.2 热羽流与送风射流相互作用的计算方法验证

基于上述的数值计算模型，对热羽流与送风射流相互作用理论进行验证。模型示意图如图2（a）所示，模拟房间大小为4m×4m×3m（L×W×H），房间底部距两边侧墙0.5m的长方形设为出口，顶部整个吊顶设为送风速度入口。

为了更好的验证两个气流的相互作用，本文对不同热源大小（70W，100W，250W，300W）和不同送风速度（0.25m/s—0.7m/s）多个工况进行了数值模拟验证。基于两气流相互作用理论式（13）和Realizable-湍流模型以及速度入口边界条件，在弥散吊顶通风系统下，对点热源产生的热羽流与送风射流的相互作用面高度进行数值模拟，并与理论公式结果进行对比。不同工况下的相互作用面高度绝对误差如图5所示。

结果表明，模拟结果与理论结果的作用面高度曲线变化趋势基本一致。理论结果与模拟结果的差异较小，相对误差均在20%以内。因此，由理论公式得到的作用面高度是合理的。

图5 不同热源下相互作用面高度模拟值与理论值对比

2.3 热羽流浮力

由热源羽流理论公式可知，当热羽流单独作用时，热羽流所受的浮力在某一截面成高斯分布，且该截面一般为圆形截面。该截面上的单位面积浮力大小与距离地面高度的示意图如图6所示。图6中当距离地面高度一定时，单位面积上的浮力大小随着热源功率的增大而增加，这是由于高度一定时，面积相同，不同的热源功率对应不同的浮力通量所导致的。当考虑送风射流时，如果要使得热羽流与送风射流相互作用的高度保持一致，不同的热源功率对应需要不同的送风速度，热源功率大小与所需送风速度成正比。

图6 单羽流作用时单位面积的浮力与高度的关系图

不同热源大小下热羽流所受的浮力通量0大小如表1所示。热羽流所受浮力通量随热源增加而显著增大。

表1 不同热源大小的浮力通量值

2.4 点热源气流相互作用特性分析

热源功率、送风速度与送风温度对室内热舒适和室内空气品质有重要的影响。在上述理论方法的基础上，进一步研究了不同热源大小、送风速度与送风温度下房间DCV系统的气流相互作用面高度。

2.4.1 不同热源大小下的作用面高度

图7 不同热源大小下的作用面高度

热源大小对作用面高度的影响如图7所示。根据两气流相互作用理论，送风速度一定时，相互作用面高度会随着热源功率的增大而增高。这是因为室内热源功率越大，需要更多的送风气流来平衡热羽流所产生向上的浮力。送风速度越大，相互作用面高度随着热源功率大小的增大而缓慢增加，如图7中速度0.7m/s曲线所示。送风速度越小，相互作用面高度随着热源功率大小的增大而快速增加。

2.4.2 不同送风速度下的作用面高度

图8中，在相同热源功率下，作用面高度随送风量的增加而逐渐减小。送风速度的增加导致送风动量的增加，根据上述理论公式，相同热源作用下作用面高度随着送风速度的增加而减小。当室内人员（100W）坐着办公时，热源高度约为1.1m，房间高度为3m。利用体热源的羽流量公式，根据送风速度与作用面高度的关系图，为满足室内人员活动区的舒适性要求，最低的送风速度约为0.11m/s，最大的风速为0.35m/s。同理，当室内人员（100W）站着活动时，热源高度约为1.7m，此时，送风速度范围是0.11m/s—0.15m/s。

图8 不同送风速度下作用面高度

2.4.3 不同送风温度下的作用面高度

在研究密度与作用面高度关系中，采用不同的送风温度（16℃—26℃），共设置4个工况，70W、0.2m/s，100W、0.3m/s，150W、0.4m/s，200W、0.5m/s。其余设置保持不变。

图9为热羽流和送风射流相互作用面高度与送风温度的关系图。在模拟中，假设送风温度分别是16℃—26℃，间隔2℃。由图可知，不同送风温度下，两气流的相互作用面高度变化不大。由于室内环境温度与送风射流温度的温差变化很小，所以密度差变化很小。因此，在相同热源和送风速度下，作用面高度变化不大。

图9 不同送风温度下相互作用面高度

2.5 面热源与体热源气流相互作用特性分析

2.5.1 面热源下气流相互作用特性分析

图10 热源直径与作用面高度的关系图

图11 热源面积与作用面高度的关系图

通过两气流作用面高度与热源直径的关系图10可以直观地看出，两气流的相互作用面高度与热源直径大小呈线性关系，作用面高度随着热源直径的增加而均匀减小。图11表明了两气流的相互作用面高度与热源面积呈负相关的关系，作用面高度随着热源面积的增加而减小，当面热源面积趋近于0时可以近似看成点热源，此时的相互作用面高度与点热源的模拟高度的误差在10%以内。

2.5.2 体热源下气流相互作用特性分析

图12表明了两气流的相互作用面高度与热源高度的关系。当热源高度变化1.6m时，热羽流与送风射流的相互作用面高度最多变化0.2m，因此，可以认为作用面高度随着热源高度的增加会缓慢减小。当体热源的热源高度变为0时，此时体热源就变为面热源，相同条件下的作用面高度与面热源的作用面高度误差在10%以内。

图12 体热源高度与作用面高度关系图

3 结论

本文通过理论分析和数值模拟研究了弥散吊顶通风系统下热羽流与送风射流相互作用，得出的主要结论如下：

（1）采用弥散吊顶通风系统时，室内某一高度存在强烈的气流混合区域，在该混合区域中，送风射流的动量变化与热羽流上升的浮力相当。

（2）通过动量守恒定律推导了单独点热源作用下热羽流与送风射流相互作用理论高度，其计算公式为：

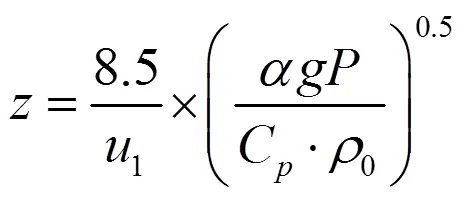
（3）两气流的相互作用高度随热源功率大小的增加而增加；随送风速度的增加而减小；且当热源大小与送风速度一定时，与送风温度基本无关。

本文研究了在弥散吊顶通风系统下点热源、面热源与体热源的气流相互作用特性分析，得到了相关气流相互作用高度的理论公式，可完善弥散吊顶通风系统原理方面的研究，有助于弥散吊顶通风系统的推广。

[1] B Yang, A K Melikov, et al. A review of advanced air distribution methods - theory, practice, limitations and solutions[J].Energy and Buildings, 2019,202:109359.

[2] A Wagenberg, M A H H Smolders. Contaminant and heat removal effectiveness of three ventilation systems in nursery rooms for pigs[J]. Transactions of the American Society of Agricultural Engineer, 2002,45(6).

[3] L Jacobsen. Air motion and thermal environment in pig housing facilities with diffuse inlet: PhD thesis, Department of Civil Engineering[D]. Aalborg University, Denmark, 2008.

[4] Tao Yu, P Heiselberg, B Lei. A novel system solution for cooling and ventilation in office buildings: A review of applied technologies and a case study[J]. Energy and Buildings, 2015,90:142-155.

[5] Tao Yu, P Heiselberg, B Lei. Experimental investigation of cooling performance of a novel HVAC system combining natural ventilation with diffuse ceiling inlet and TABS[J]. Energy and Buildings, 2015,90:165-177.

[6] Chen Zhang, Martin Heine Kristensen, Jakob Søland Jensen, et al. Parametrical analysis on the diffuse ceiling ventilation by experimental and numerical studies[J]. Energy and Buildings, 2016,111:87-97.

[7] 赵江东,余涛,雷波.弥散式吊顶送风在商场内区冬季供冷中的适用性分析[J].制冷与空调,2019,33(4):414-420.

[8] Chen Zhang, PerKvolsHeiselberg, Qingyan Chen, et al. Numerical analysis of diffuse ceiling ventilation and its integration with a radiant ceiling system[J]. BUILD SIMUL, 2017,10:203-218.

[9] G K. Heat convection and buoyancy effects in fluids[J]. Q. J. R. Met. Soc., 1954,80:339-358.

[10] Hakon skistad(ed), Elisabeth Mundt, Peter V Nielsen, et al. Displacement ventilation in non-industrial premises[M]. Norway: Federation of European Heating and Air-condition Associations, 2002.

[11] Morton, G I Taylor, J S Turner. Turbulent gravitational convection from maintained and instantaneous sources [J]. Proc. R. Soc. Lond. A, 1956,234:1-23.

[12] Hunter Rouse, Chiashun Yih, H W Humphreys. Gravitational Convection from a Buoyancy Source[J]. Tellus, 1952,4:201-210.

[13] Turner J S. Buoyancy effect in fluids. Cambridge[M]. University Press, Cam-bridge, 1973.

[14] 赵鸿佐.室内热对流与通风[M].北京:中国建筑工业出版社,2010.

[15] 张强,朱树园,周宇.圆形和圆柱形热源羽流计算方法的研究[C].全国通风技术交流大会,2007.

[16] 李先庭,赵彬,邵晓亮,等.建筑通风[M].北京:机械工业出版社,2002.

[17] 高晓攀,李安桂.基于工业厂房相邻热源耦合热羽流特性的热压自然通风研究[D].西安:西安建筑科技大学,2018.

Analysis of the Airflow Interaction Principle of Diffuse Ceiling Ventilation System

Shi Pandi Yu Tao Yuan Yanping

( School of Mechanical Engineering，Southwest Jiaotong University, Chengdu, 610031 )

Diffuse ceiling ventilation system is a new type of ventilation method using porous ceiling panels as the terminal device to supply air to the room, which can supply low-temperature air into the room without any cold draught in the occupied zone. However, there is still a lack of relevant research on the interaction principle between the heat source thermal plume and the supply air jet in this ventilation system. In this paper, a combination of theoretical analysis and numerical simulation is used to establish the interaction model of the supply air jet and the thermal plume of the diffuse ceiling ventilation system. The interaction pattern of the thermal plume and the supply air jet is studied. Results show that the thermal plume and the supply air jet strongly mix with each other at a certain height, and the buoyancy effect of the thermal plume in the mixing area is equal to the momentum of the supply air jet. The height of the interaction surface increases with the heat source power but decreases with the supply air speed. When the power of the heat source and the supply air speed are constant, the buoyancy of the thermal plume is almost constant, and the height of the interaction surface is basically independent of the supply air temperature. Research in this paper can provide theory for the design of diffuse ceiling ventilation system.

diffuse ceiling ventilation; thermal plume; supply air jet; buoyancy effect

TU831

A

1671-6612（2021）02-143-08

四川省科技厅重点研发项目——川西高原居住建筑太阳能通风内墙的传热机理与应用研究（19ZDYF0452）；国家自然科学基金青年科学基金项目——耦合太阳能热源的空心通风内墙蓄传热特性研究（51708453）；百叶遮阳“二次得热”的预测及控制研究（2019-YF05-01326-SN）

石盼弟（1996.04-），女，在读硕士研究生，E-mail：swjtu_spd@163.com

余 涛（1987.08-），男，博士，讲师，硕士生导师，E-mail：yutao073@swjtu.edu.cn

2021-01-26