高速列车隧道交会流场模拟
2021-05-19田栋栋
田栋栋 王 文
高速列车隧道交会流场模拟
田栋栋 王 文
(陕西铁路工程职业技术学院 渭南 714000)
采用计算流体力学软件Fluent,选用RNG-湍流模型,建立列车隧道交会时的二维动网格模型,对高速列车隧道交会引起的空气动力学效应进行了二维非定常数值模拟,分析列车交会时隧道内流速、压力分布变化规律。研究表明:两车交会时,两车中间部分压力值最小,靠近隧道壁面侧的压力较大,且两侧压力成对称分布;两车中间流场速度在0m/s附近波动,靠近隧道壁面侧形成明显环隙流;靠近车体部分由于拖曳力作用与车行方向同向,靠近壁面部分与车行方向相反,且所占空间较大;初交会时,列车头部挤压作用叠加,环隙流速、压力均有较大增幅;两车相离时,车尾部尾涡作用叠加,尾部涡流影响减弱。
隧道;列车交会;空气动力学;数值模拟
0 前言
高速列车通过隧道时,由于车头部分挤压作用,会使隧道压力突然增大,在隧道内形成活塞风。但隧道两车交会时,由于压缩波的叠加,隧道内流场、压力场变化较为复杂。同时高速列车隧道交会过程的研究对于行车安全及车体设计具有重要的意义。
周丹等[1]基于Fluent软件,选用标准-双方程湍流模型,采用滑移网格方法,对不同编组长度高速列车明线交会以及于各自最不利长度隧道通过和交会工况进行模拟,并对车体表面产生的交变压力载荷进行研究。魏洋波等[2]基于Fluent软件,选用标准-双方程湍流模型,采用滑移网格技术,对高速列车明线交会及隧道内交会时的空气流场进行数值模拟,研究不同线间距对高速列车交会压力波的影响。刘冬雪等[3]采用CFD软件Fluent,模拟研究了A型地铁列车在隧道内加减速时车体表面压力变化和车内压力变化,分析隧道净空面积与密封指数的关系,并采用动模型实验验证数值计算准确性。梅元贵等[4]采用STAR-CD软件,建立了列车几何模型和非定常可压缩湍流的三维流动模型,对高速列车隧道内等速和不等速交会的全过程进行了数值模拟。许建林等[5]基于CFD软件,采用三维可压缩非定常湍流流动的模型压力修正算法和任意滑移界面网格技术,对高速列车隧道内等速和不等速交会压力波进行数值模拟,分析了列车交会过程中车体外部压力场的变化。徐伟等[6]基于三维非定常不可压缩流动的N-S方程,采用LES湍流模型和动网格算法,对CRH2动车组以100m/s的速度通过长100m的隧道进行了动态数值模拟计算。
本文基于Fluent软件,选用RNG湍流模型和动网格技术,对高速列车隧道交会引起的空气动力学效应进行了二维非定常模拟,分析隧道内流速、压力分布变化规律,为车头结构进一步优化、对于隧道交会车速的确定提供参考。
1 数值模型
1.1 模型的建立
列车隧道交会引发的隧道空气流场是复杂的三维流动,但三维数值模拟对计算机硬件要求高,且计算效率低下。根据相关文献[7],二维模型能与理论分析结果较好的契合。本文采用二维模型,对隧道内列车交会过程进行非定常数值模拟。计算模型如图1所示。

图1 列车隧道交会示意图
1.2 基本方程
采用基于Navier-Stokes方程的风流模型,选取RNG湍流模型使方程组封闭。隧道内空气湍流流动用到的控制方程包括基本控制方程(连续性方程、动量方程、能量方程)、-模型方程和组分方程。方程形式如下:
基本控制方程通式:

方程:

方程:
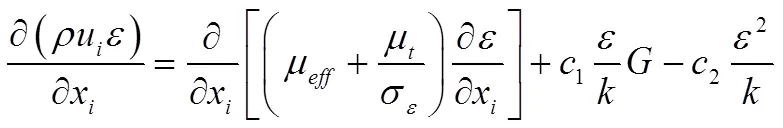
其中

式中:为待求通用物理量;Γ、S分别为对应变量的输运系数和源项;u为速度分量,m/s;为紊流动能,m2/s2;为紊流的动能耗散率,m2/s3;为紊流脉动动能产生项;为流体密度,kg/m3;为层流动力黏性系数,Pa·s;μ为紊流动力黏性系数,Pa·s;1、2、σ、σ、c为经验常数,1=1.44,2=1.92,σ=1.30,σ=1.00,c=0.09。
1.3 边界条件
(1)入口边界为压力入口,出口边界为压力出口,压力均为0Pa。
(2)隧道壁面为无滑移、绝热边界,粗糙度设为0.008m。
2 动网格模型的建立
2.1 动网格计算模型
对于通量,在任一控制体内,其边界是运动的,守恒方程的通式为:


2.2 程序的二次开发
建模中考虑列车运动带来的流场随时间改变的问题,采用Fluent软件建立动网格模型。将列车边界设置为动壁,两车用car1、car2区分。运用Fluent软件提供的DEFINE_CG_MOTION宏,用C语言编译列车运动的UDF。列车匀速相向而行,速度=56m/s,计算总时长=12s。
2.3 数值算法
列车交会过程的流场采用非定常隐式解法,选取RNG-ε湍流模型,流场迭代采用PISO(Pressure Implicit with Splitting of Operators)算法,压力场采用标准离散方式,其他采用二阶迎风格式离散。本文动网格计算中网格的动态变化过程选用弹簧近似光滑模型(spring-based smoothing)和局部重划模型(local remeshing)模型进行计算。时间步长设置为0.005s。
3 模型验证
Pope C W等[8]对帕斯威隧道内不同列车车型在隧道内运行所引起的活塞风和压力波进行了实测研究。隧道全长=1140m,隧道当量直径=4.97m,列车长度=196.6m,阻塞比=0.4,列车平均速度取35m/s。风速计布置在距隧道入口150m处,距边墙0.5m。
研究以实际隧道为模型,简化建立二维动网格模型。基于Fluent软件,选用RNG-ε湍流模型,对测点流速变化进行监测,并将模拟结果与试验结果进行比较验证,结果如图2所示。
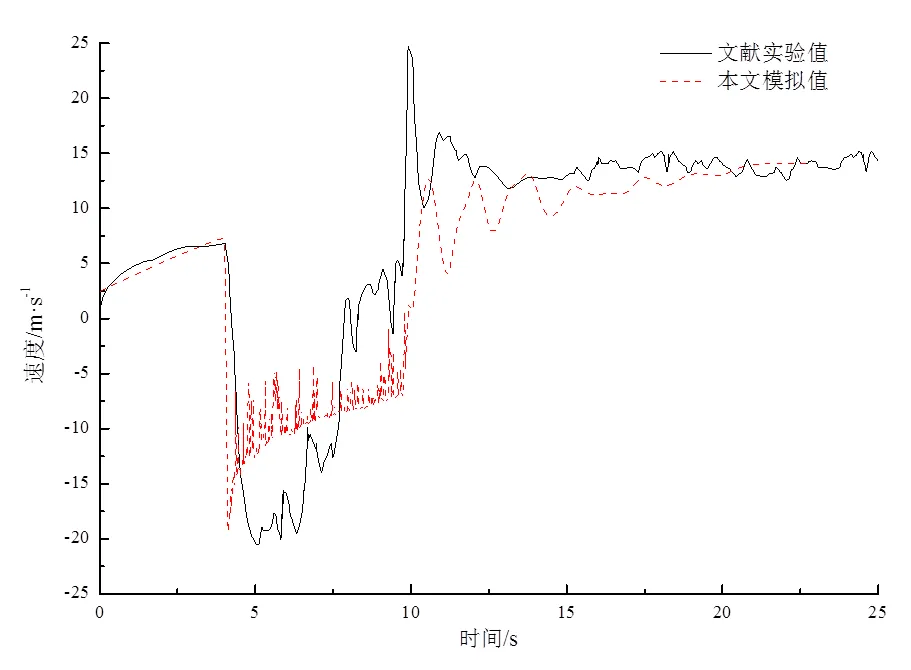
图2 模型验证
由图2可以看出,隧道内150 m处测点风速试验值与模拟值变化趋势较为一致,由于二维简化原因,在列车通过测点位置时的环隙流速存在较大差异。利用二维动网格模拟列车交会流场,具有一定的可行行和可信度。
4 结果与分析
列车在隧道交会前后,隧道内及车体周身流场分布区别明显。截取两车未交会和交会不同时刻两种工况下车头附近流场分布图(图3~图7),对其分布规律进行分析。
工况1:列车交会前
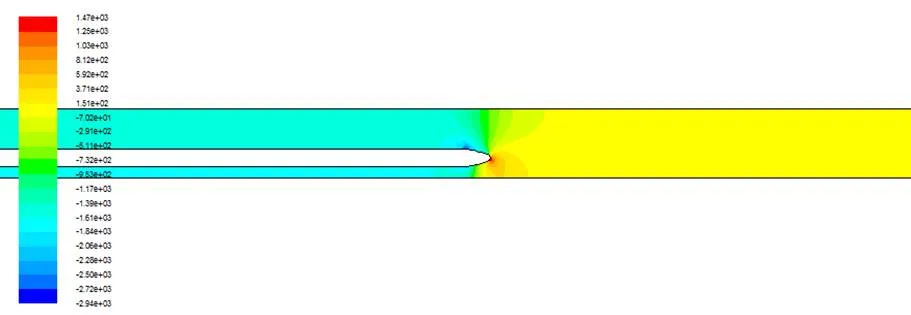
图3 交会前压力云图

图4 交会前流线图
由图3可以看出,因为隧道本身空间分布及相向列车压缩波的影响,车头鼻尖处压力分布不以车体中线呈对称分布,鼻尖高压力偏向靠近隧道壁面侧。由图4可以看出,流体部分沿车体与隧道形成的环隙空间向车行反方向流动,车头前方由于压缩波的作用,在隧道中呈型分布,与车行方向同向。且型分布只在靠近车头部的一定距离内,远离该距离时流场不在呈型分布。由于车体为无滑移壁面,将产生一拖曳力,故隧道中最大速度都是靠近车体表面部分。
工况2:列车交会
两车交会时,随着两车持续交错运行,隧道内速度、压力变化极为复杂,不同交会时刻下隧道内流场分布如图5~7所示。

图5 交会速度云图
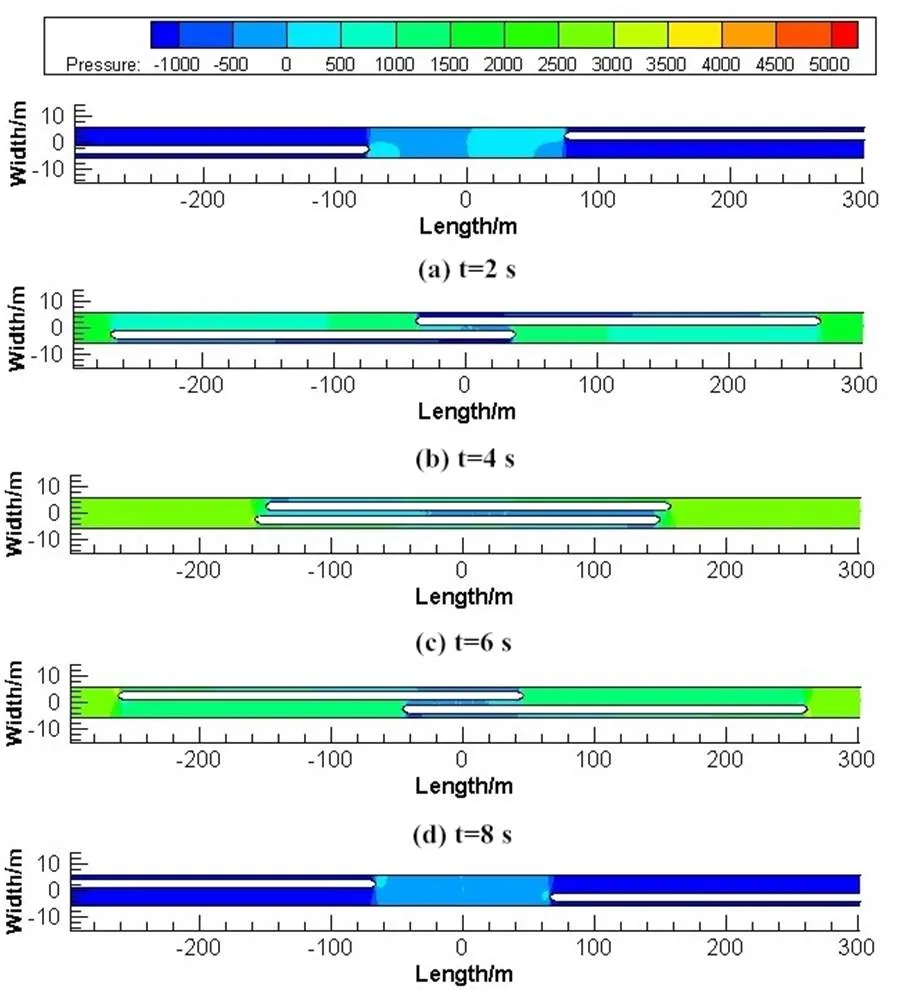
图6 交会压力云图
由图5可以看出,两车初相遇时,由于车头挤压作用,使活塞风与环隙流形成叠加,各车头前端流场流速较单车运行跟大,且流向与车行方向一致。两车相离时,各车尾部由于负压涡流区作用的相互抵消,流速很快归于0m/s附近。由图6可以看出,随着两车交会过程的进行,列车鼻尖处最大压力值逐渐增大。且负压值也增大,整个压力变化幅度变宽。两车相离后,由于尾涡作用的叠加,隧道交会点处压力很快归于稳定。

图7 矢量、流线图
由图7可以看出,两车初交会时,车头挤压作用明显,车身与壁面空间形成较高流速的环隙流场,与车行方向异相。两车相离时,在车尾形成尾涡区,两个尾涡相互干扰,使尾涡偏向隧道壁面侧,随着两车进一步相离,两车尾涡的作用相互抵消,交会点速度、压力快速达到稳定状态。
为分析列车交会时环隙流的分布变化,在两车交会中间点处设置监测线,对两车交会时环隙流场做模拟分析,结果如图8所示。
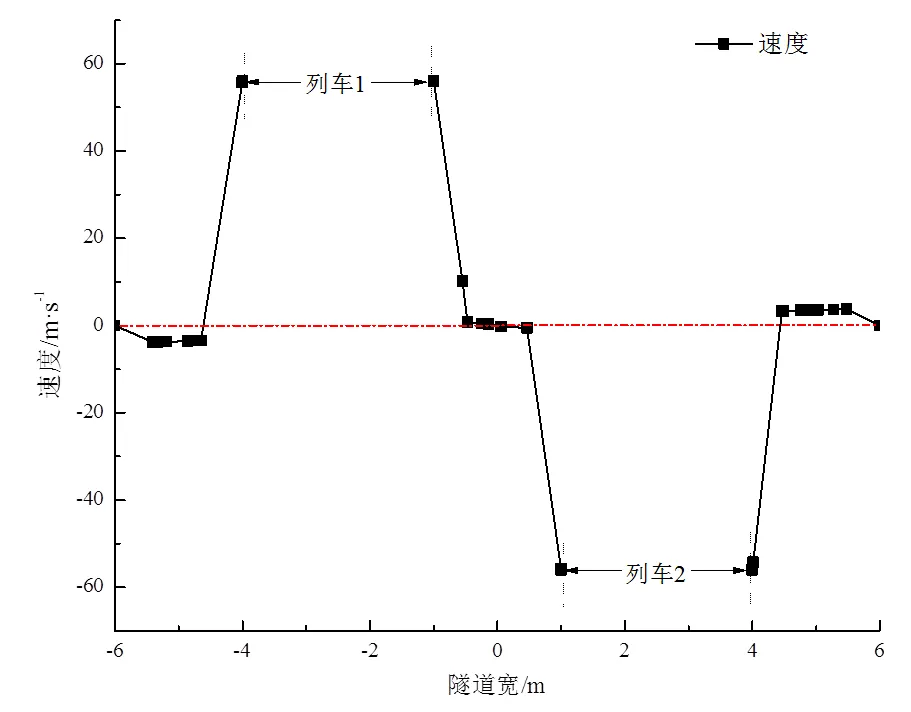
图8 环隙速度分布
由图8可以看出,两车交会时,由于两车拖曳力相互叠加作用,两车中间空间速度维持在0 m/s附近波动。而在靠近隧道壁面侧形成明显环隙流场,除靠近车体部分由于曳力作用与车行方向同向,其他空间部分环隙流方向与车行方向相反。
在两车交会点设置监测线,用以监测列车车距逐渐缩小过程中,隧道速度、压力在该位置时的纵向分布。监测结果如图9、10所示。
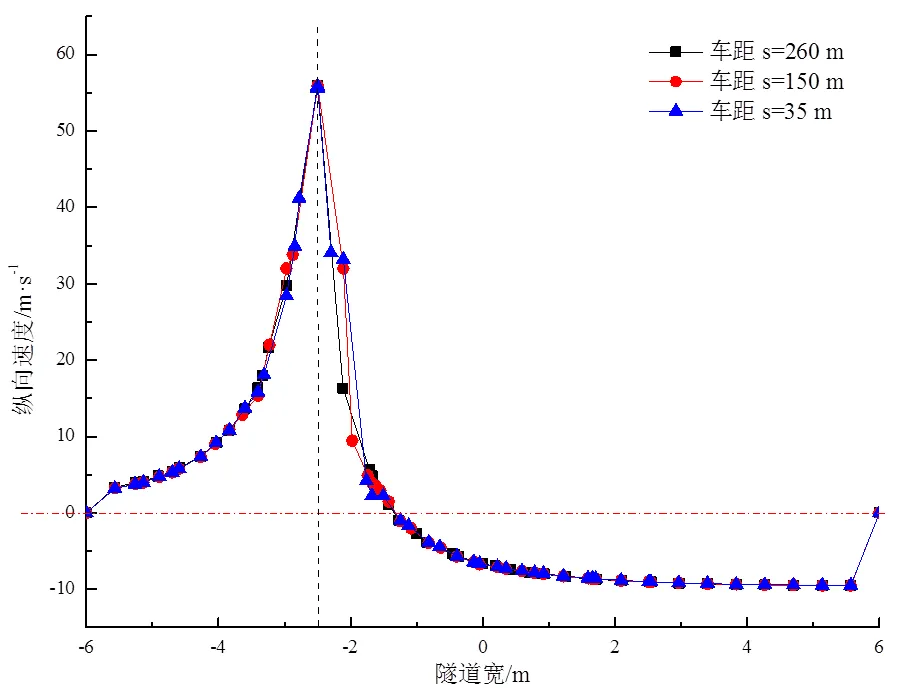
图9 速度分布

图10 压力分布
由图9可以看出,近壁侧速度均与列车车行方向一致,越靠近列车壁速度越大。远壁侧速度与列车车行方向相反,且由于列车动壁及隧道静壁曳力的作用呈型分布。由图10可以看出,由于相向列车活塞风及隧道空间的影响,列车鼻尖处最高压力偏向近壁侧。且近壁侧压力呈正压,远壁侧压力呈负压。
为分析列车头部速度、压力的分布变化规律,在距车鼻尖不同位置设置监测线,监测结果如图11、12所示。
由图11、12可以看出,随着测点与鼻尖间距的增大,列车头部最大速度及压力值逐渐降低,且下降幅值逐渐减小。距鼻尖越近,其速度与压力在近壁区呈最大正值,在远壁区呈最大负值。

图11 列车头部速度分布

图12 列车头部压力分布
5 结论
研究基于数值模拟软件Fluent,选用RNG湍流模型,采用动网格技术对高速列车隧道交会引起的隧道内流速、压力分布变化规律进行非定常分析,主要结论如下:
(1)通过模型验证,表明采用动网格技术对隧道内列车运行流场分析的方式可行,计算结果可靠。
(2)随着列车逐渐靠近,两列车头部速度、压力都偏向近壁区,且距离越近偏离幅值越大。两车尾部涡流相互影响作用,使涡流靠近隧道壁面侧。
(3)近壁侧速度均与列车车行方向一致,越靠近列车壁速度越大。远壁侧速度与列车车行方向相反,且由于列车动壁及隧道静壁曳力的作用呈型分布。近壁侧压力呈正压,远壁侧压力呈负压。
(4)列车头部挤压作用相互叠加,隧道内环隙流速增大。列车尾部涡流区叠加,使涡流影响减弱,车尾后部流场很快回归稳定。
[1] 周丹,贾丽荣,牛纪强.编组长度对高速列车表面交变压力载荷的影响[J].铁道科学与工程学报,2018,15(1):1-7.
[2] 魏洋波,梁习锋.线间距对交会压力波的影响研究[J].铁道科学与工程学报,2017,14(12):2525-2531.
[3] 刘冬雪,蒋雅男,杨明智.加减速时地铁列车隧道气动性能研究[J].铁道科学与工程学报,2018,15(1):178-187.
[4] 梅元贵,孙建成,许建林,等.高速列车隧道交会压力波特性[J].交通运输工程学报,2015,15(5):34-43.
[5] 许建林,孙建成,梅元贵,等.高速列车隧道内交会压力波基本特性数值模拟研究[J].振动与冲击,2016,35(3): 184-191.
[6] 徐伟,杨翊仁,张明禄,等.高速列车通过隧道时的气动特性研究[J].应用数学和力学,2014,35(S1):123-126.
[7] 王一伟,杨国伟,黄晨光,等.隧道长度对高速列车交会压力波的影响研究[J].中国科学:技术科学,2012,42(1): 82-90.
[8] POPE C W. Transient pressures in tunnels-A formula for predicting the strength of the entry wave produced by trains with streamlined and unstreamlined nosed[J]. British railway board tech aero, 1976,12.
Simulation of the Flow Field of the High-speed Train Meeting in the Tunnel
Tian Dongdong Wang Wen
( Shaanxi Railway Institute, Weinan, 714000 )
Using the computational fluid dynamics software Fluent and the RNG-turbulence model, a two-dimensional dynamic grid model at the intersection of train tunnels was established, and the aerodynamic effects caused by the intersection of high-speed train tunnels were simulated with two-dimensional non-constant values to analyze the train During the intersection, the flow velocity and pressure distribution in the tunnel change. The research shows that: when the two vehicles meet, the pressure value in the middle of the two vehicles is the smallest, the pressure near the tunnel wall is greater, and the pressure on both sides is symmetrically distributed; the velocity of the intermediate flow field of the two vehicles fluctuates around 0 m/s, and an obvious annular flow is formed near the tunnel wall; the part close to the car body is in the same direction as the driving direction due to the towing force, and the part close to the wall surface is opposite to the driving direction, and takes up more space; at the initial meeting, the squeezing effect of the train head is superimposed, and the annulus flow velocity and pressure are greatly increased; when the two vehicles are separated, the tail vortex effect of the parking space is superimposed, and the effect of the tail vortex is weakened.
tunnel;train rendezvous;aerodynamics;numerical simulation
U459.1
A
1671-6612(2021)02-169-06
陕西铁路工程职业技术学院科研项目(KY2017-032)
田栋栋(1987-),男,硕士研究生,讲师,E-mail:745908351@qq.com
2020-06-30
