BP神经网络和曲率模态理论在桥梁损伤识别中的应用

2021-05-18包龙生孟宪彪张筱薇

沈阳建筑大学学报（自然科学版） 2021年2期

包龙生，曹悦,2，赵宁，孟宪彪，张筱薇

(1.沈阳建筑大学交通工程学院，辽宁沈阳 110168；2.沈阳建筑大学土木工程学院，辽宁沈阳 110168；3.山东省交通科学研究院，山东济南 250100； 4.中铁十九局集团轨道交通工程有限公司，北京 101300；)

近年来，国内老旧桥梁倒塌事故频频发生，给社会带来了重大人员财产损失，因此桥梁全寿命周期内的安全问题越来越受到人们的重视[1]。为了避免此类事故的发生，如何实时准确地了解桥梁结构的状态并评判其安全性是桥梁管理部门核心要务。桥梁健康监测系统能够满足桥梁管理管理部门的需求，但起初受到传感器精度、环境、稳定性等因素的制约而未能广泛使用，后随着传感器技术的飞速发展，桥梁健康监测的精度和准确性大幅提高，越来越多的桥梁配备了桥梁健康监测系统[2-5]。桥梁健康监测系统应用范围的拓宽使桥梁健康监测逐渐成为土木工程学科中一个比较重要的研究领域[6-7]。桥梁在运营时伴随着各式各样的荷载和环境影响，会给结构带来不同程度的损伤。

当结构发生损伤时，一般会伴随着截面破损，甚至材料弹性模量的退化，如何在桥梁健康监测系统产生的大量数据中抓取有效的损伤指标是非常重要的。频率[8]和阻尼比常常会被作为评判结构是否发生损伤的指标，但通过对大量桥梁动载试验结果分析后，发现当桥梁未发生一定程度的结构性损伤时，频率及阻尼比并没有明显的变化，识别效果不明显[9]。而基于结构动力特性的指标，如振型、曲率模态、应变模态等[10-12]进行结构损伤识别时相比于频率和阻尼比，具有更好的敏感性[13-17]。

桥梁结构在进行健康监测时往往会采集大量的数据，在大量数据中能够快速分析出结果对于实际工程快速定损有很大的意义。人工神经网络作为一种基于仿生学理论的信息处理系统，可模仿人类大脑对外界信息进行处理，因其对信息处理的并行性、自学性、自组性及鲁棒性等优势，近些年被广泛应用于土木工程等相关领域[18]。应用大量测试数据对神经网络进行训练，可代替人工进行运算，从而快速地识别损伤位置及程度。张强等[19]通过BP神经网络系统对截齿磨损程度类型进行准确监测及识别。王柏生、郭杏林等[20-21]通过使用固有频率结合神经网络对结构发生的损伤进行验证，获得了比较理想的结果。

基于此,笔者使用专业编程软件编写程序，与有限元数值模拟数据直接对接,应用模态数据曲率化数据集对BP神经网络进行训练，再通过训练后的BP神经网络对结构损伤进行预测，最后结合最常见的两种桥型对该程序进行验证。研究表明:笔者开发的程序可以对桥梁的损伤进行很好地识别及预测，并可以智能输出。

1 基本理论与假设

1.1 曲率模态理论

在桥梁结构中，主梁作为主要受力构件，一般为受弯构件，主要以弯曲变形为主，其余变形如剪切变形可忽略不计。因此通过对虚功原理进行简化，其挠度表达式:

(1)

图1为桥梁挠曲线示意图，其中θ为转角，yi为挠度，曲线曲率公式为

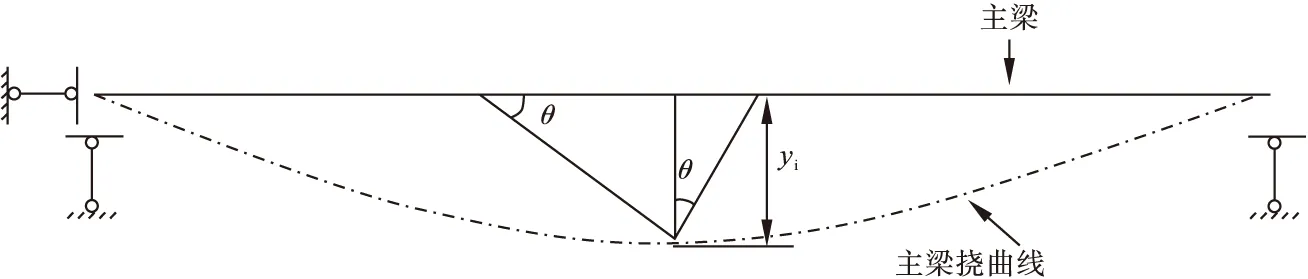
图1 挠曲线示意图Fig.1 Schematic diagram of deflection curve

(2)

式中:ρ(x)为曲率半径。

式(2)可转化为

(3)

梁内截面处弯矩与挠度有如下关系:

(4)

结合式(3)、式(4)可得出:

(5)

由式(5)可知主梁上某一点的曲率与其对应的刚度成反比，所以结构的刚度一旦发生变化，便可以通过曲率反映出来[22]。

在实际工程结构中，通常会在主梁上预先布置各类传感器，如GPS传感器、北斗传感器或其他位移传感器来配合采集系统实时采集结构的振动情况[23]，即采集桥梁测点在某一时刻的位移δ(xi)，经计算后便可得到结构整体的位移阵型δ，公式如下:

δ=[δ(x1)δ(x2)…δ(xi)…δ(xn-1)δ(xn)].

(6)

式中:i为布置传感器的个数。

曲率模态ρ(xi)可由位移阵型中心差分法求得，其计算公式:

(7)

式中:li-1,i为传感器i-1到i的距离；li,i+1为传感器i到i+1的距离。

实际计算时通常对曲率模态数据进行归一化处理，从而使损伤指标更加敏感。

1.2 BP神经网络

BP神经网络通过对人类大脑中的神经元应对外部刺激反应的模仿，建立多层感知模型，通过对信号进行正方向的传递，得到误差后再反向进行调节，不断地进行迭代试错学习，最终形成能够处理非线性信息的智能网络模型[24]:

(8)

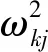
搭建好神经网络模型后，将模态参数作为神经网络的输入变量，以结构损伤指标为输出变量，利用神经网络的训练自学能力，使神经网络掌握输入变量与输出变量之间的非线性映射，从而实现损伤评估。

基于上述理论，桥梁结构损伤识别的流程如图2所示。

图2 BP神经网络结构损伤识别的流程图Fig.2 Flow chart of structural damage identification based on BP neural network

2 数值模拟与分析

分别对常见的两种桥梁结构进行仿真分析，验证该方法的可行性。编制的程序部分核心代码如下:

load data_data.mat

damage_curvature_Mode=diff(damage_mode，2)/x

undamage_curvature_Mode=diff(undamage_mode，2)/x

temp=randperm(size(damage_mode,1));

P_train=damage_mode(temp(1:n),:)′;

T_train=degree_of_damage(temp(1:n),:)′;

…

figure

plot(1:N,T_test,′b:*′,1:N,T_sim,′r-o′)

legend(′真实值′,′预测值′)

xlabel(′预测样本′)

ylabel(′损伤程度′)

string={′测试集损伤程度预测结果对比′;[′R^2=′ num2str(R2)]};

title(string)

bar3(curvature_difference)

xlabel(′测试集编号′);ylabel(′节点编号′);zlabel(′曲率模态差′)

2.1 简支结构模拟

案例1:以某简支梁桥结构为研究对象，简支梁结构总长10 m，整桥划分20个单元，材料弹性模量为3.45×104MPa。预设损伤时考虑到实际工程中一阶模态较易采集，因此仅仅采用一阶模态数据进行仿真分析。预设损伤程度为5%～20%，损伤设置为单一损伤，损伤模拟采用刚度折减实现，损伤位置从2号单元至19号单元依次对每个单元设置单一损伤，共得到72组数据。简支梁结构简图见图3。

图3 简支梁结构简图Fig.3 Simple beam structure diagram

再利用Matlab软件编制程序，对神经网络参数进行设置，迭代次数设置为1 000次，训练精度设置为10-3，学习率设置为0.01。通过案例1模态分析得到的72组训练集经开发的程序进行随机打乱次序处理，乱序后训练集中的输入变量与输出变量依然一一对应。取前60组数据集作为训练集，取剩余12组数据集作为测试集，经运算后输出的结果及图形如图4、图5所示。

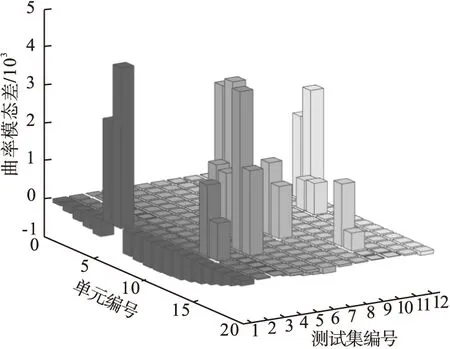
图4 简支梁测试集数据曲率模态柱状图Fig.4 Curvature mode histogram of simply supported beam test set data

从图4可以看出，12组测试集中原预设损伤单元的两边节点处均存在柱状激凸，并能够自动输出每个测试集的损伤位置。三维柱状图中不同高度的Z坐标对应不同的损伤程度，分别对应图5中12组测试集的损伤真实值。

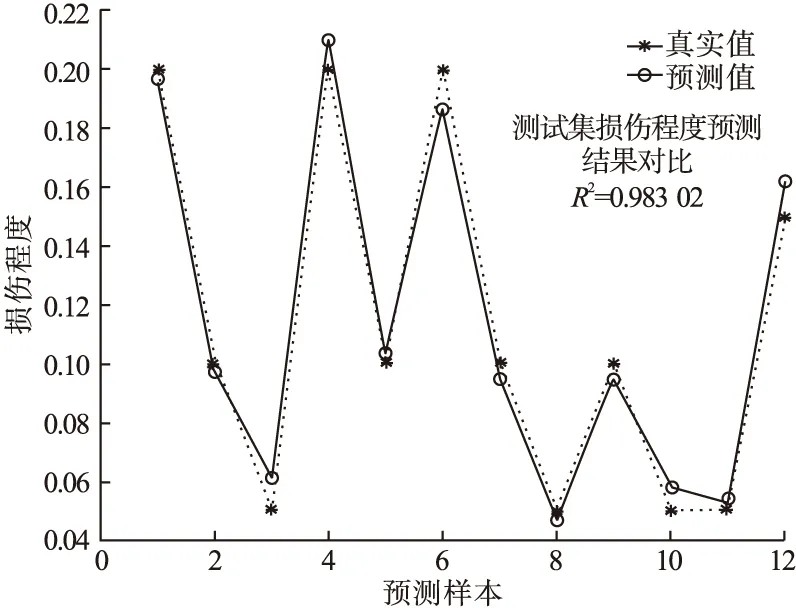
图5 简支梁测试集数据与实际数据对比图Fig.5 Comparison between test data and field data of simply supported beam

由图5可以看出，经过训练后的神经网络可对测试集损伤程度进行预测并输出。其中，真实值为提前预设的刚度损伤程度。如将结构单元划分更细致，图5中损伤处的Z坐标会更加突出。

2.2 连续梁桥数值模拟

案例2:以某3跨等截面预应力混凝土连续梁桥为研究对象，桥梁全长为106 m，跨径布置为30 m+46 m+30 m。主梁混凝土采用C50标号，桥梁纵、横断面如图6所示。混凝土弹性模量为3.45×104MPa。桥梁有限元模型共划分106个单元，损伤模拟采用刚度折减实现。应用较为容易采集的一阶模态数据进行分析。由于该桥单元划分多，故仅在第一边跨及中跨设置结构损伤，损伤位置选取表1中单元范围内的偶数单元进行设置。经整理，一共为84组数据集，损伤程度如表1所示。

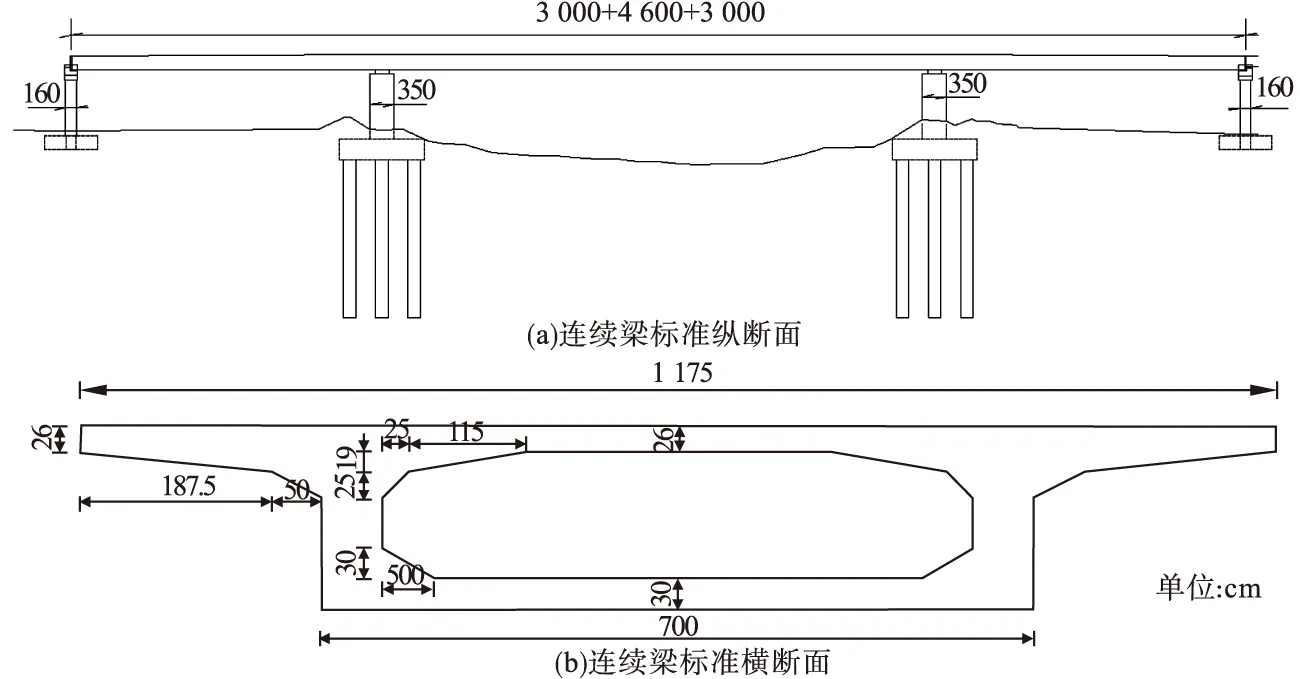
图6 连续梁立面图及横断面图Fig.6 Continuous beam elevation and cross-section diagram

表1 损伤程度表Table 1 Damage degree table

通过程序对24组测试集进行运算，输出结果如图7、图8所示。

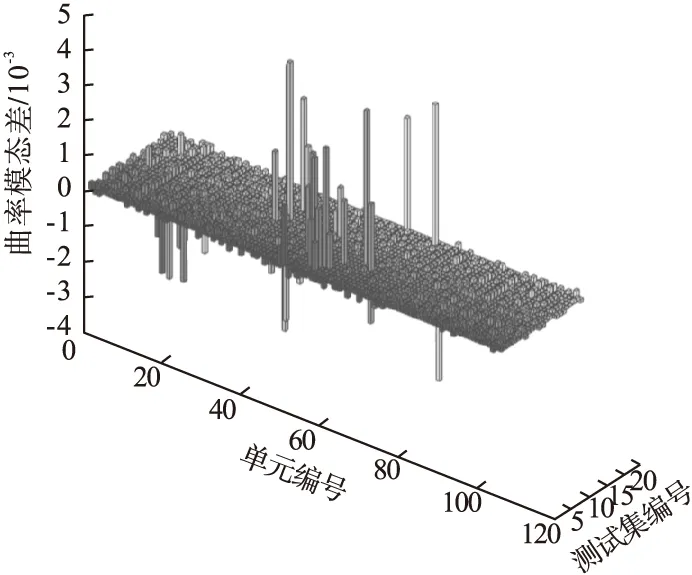
图7 连续梁测试集数据曲率模态柱状图Fig.7 Curvature mode histogram of continuous beam test set data

图8 连续梁测试集数据与实际数据对比Fig.8 Comparison between test data and field data of continuous beam

由图7可以看出，24组测试集原预设损伤单元处均存在柱状激凸，可以自动输出每个测试集的损伤位置。三维柱状图中不同高度的Z坐标对应不同的损伤程度，分别对应图8的24组测试集的损伤真实值。由图8可以看出，柱状图的方向有正有负，这是因为连续梁的振型在不同的跨得到的模态参数方向不同，当发生损伤时或大于未损伤，或小于未损伤，通过差值即存在正负不同现象。三维柱状图中测试集数量较多提取前两组测试集数据如图9所示。