基于BIM和遗传算法的填海地区深基坑支护结构优化研究

2021-05-18姜早龙张志军陈大川

沈阳建筑大学学报（自然科学版） 2021年2期

姜早龙,张杰,张志军,陈大川

(1.湖南大学土木工程学院,湖南长沙 410082;2.湖南湖大建设监理有限公司,湖南长沙 410082;3.中铁七局集团第三工程有限公司,陕西西安 710032)

目前,我国经济正步入高质量发展的新时期,为满足区域经济发展与产业布局调整的战略需要,深圳市妈湾跨海通道的建设也被提上日程。作为深圳市首条跨海隧道,建成后将极大拓展西部港区的发展空间[1]。但由于地处典型的填海淤泥地层,土体工程性质差导致极易出现基坑支护结构变形增大、地面不均匀沉降加剧等负面影响,对支护结构设计的合理性及可靠性提出了严峻考验[2]。

然而,目前我国深基坑支护结构优化设计仍采用半经验半理论的方法,技术规范性及指导性尚不完善,故不少学者对此展开了相关研究。YANG Zhuo等[3]基于改进粒子群算法建立了桩锚支护结构优化设计模型,成功降低了工程造价。蒋楠等[4]以某深基坑工程为例,运用遗传算法和非线性规划方法对支护结构设计参数进行了计算分析,并借助计算软件校核了结果的正确性。么梦阳[5]利用MIDASGTS建立了桩锚支护结构的三维模型,对桩径、桩距、锚固长度等参数进行优化，有效降低了基坑最大水平位移。宴明等[6]基于Plaxis对双排钢板桩支护结构的三维空间效应进行分析后,提出了间距优化的取值范围。刘萍[7]数值模拟了锚索倾角和锚索预应力对桩锚支护结构整体变形的影响。

通过上述研究可知,支护结构的各种优化设计方法正逐步实践于各类工程,但应用在填海地区深基坑工程的案例尚不多见。基于此,笔者以深圳市妈湾跨海通道工程为依托,围绕着填海地区深基坑支护结构优化设计展开相关研究,尝试提供一种新优化思路,以期为类似工程的优化设计提供借鉴。

1 工程简介

1.1 工程概况

妈湾跨海通道工程位于深圳市西部,沿南北向布置,南起于妈湾大道,向北依次穿过前海湾、大铲湾,最终止于大铲湾收费站和西乡大道交接处。其中填海明挖段施工里程为大铲湾侧RK5+200-RK6+200,开挖长度为1 000 m,基坑开挖平均深度主要集中为15 m,采用的支护方案为支护桩+钢筋混凝土内支撑组合(见图1)。

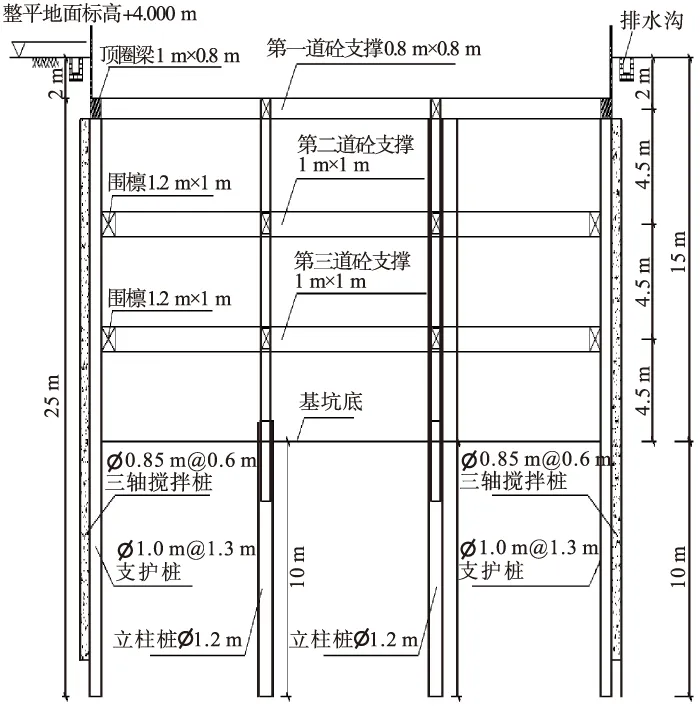
图1 基坑支护结构主要形式Fig.1 Main forms of foundation pit supporting structure

1.2 工程难点

工程地处深圳西部的填海地区,地下水丰富,受潮汐、洋流影响对支护结构产生的动力响应较大,地质条件复杂,各土层物理力学指标见表1。基坑施工范围内存在较多的流塑状淤泥,最厚处达7.2 m,大大增加了基坑上方土层纵向滑移风险。同时鉴于流塑状淤泥地层具有明显的“三高三低”特性,即含水量高、孔隙率高、压缩性高、强度低、渗透性低、固结系数低,造成在该地层成桩时孔壁易坍塌,若设计不当难以保证基坑支护结构的最终施工质量[8]。

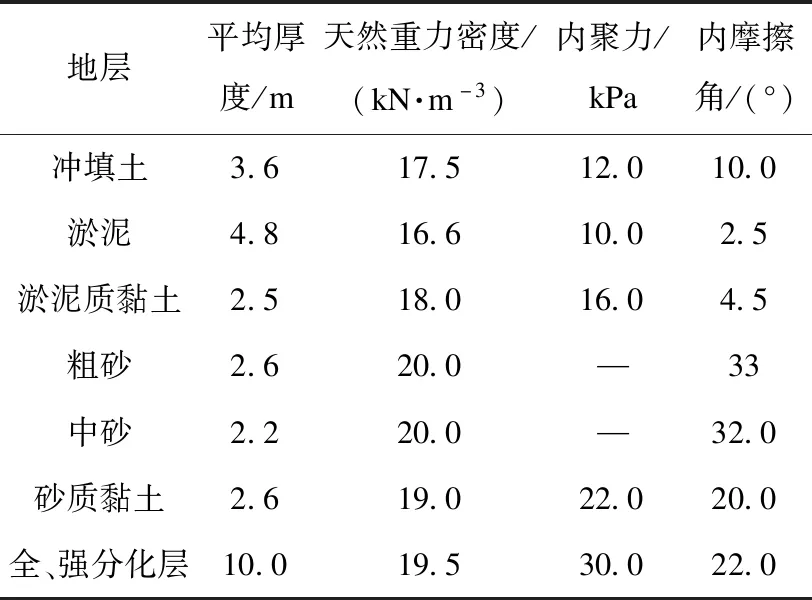
表1 各土层物理力学指标Table 1 Physical and mechanical indexes of each

2 BIM模型建立

2.1 BIM族库构建

目前BIM技术在深基坑工程方面的运用主要侧重于开挖施工的动画模拟、碰撞检测等,在深基坑工程支护结构优化设计方面的运用尚不成熟，因此,笔者在建立妈湾跨海通道深基坑支护结构BIM模型之前,先构建深基坑支护结构BIM族库,主要包括支护桩、钢筋混凝土支撑、立柱桩等(见图2)。通过BIM建模软件对上述族库的几何信息、材料信息等进行相关标注并整理归类,为后续优化数据查询及导出奠定基础。

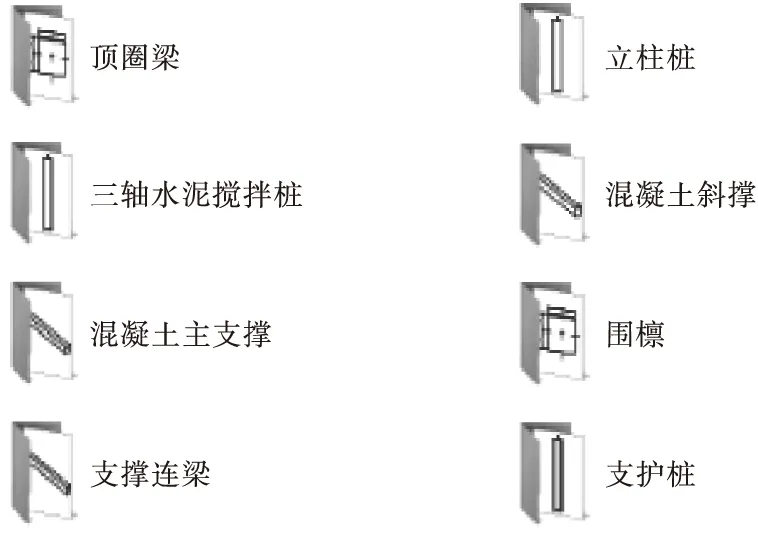
图2 支护结构BIM族库Fig.2 Support structure BIM family library

2.2 BIM模型参数化建立

填海地区深基坑工程一般多处于流塑或者软塑的海相淤泥层中,地层蠕变会让基坑支护结构变形具有较显著的时空效应[9]。为充分考虑深基坑施工的各阶段情况,应针对不同阶段的实际需求,动态收集和掌握现场信息,因此构建BIM模型时采用动态模型。在完成BIM族库构建的基础上,利用Revit软件中参数化建模方式实现支护结构的数字化、自动化建模,模型如图3所示。

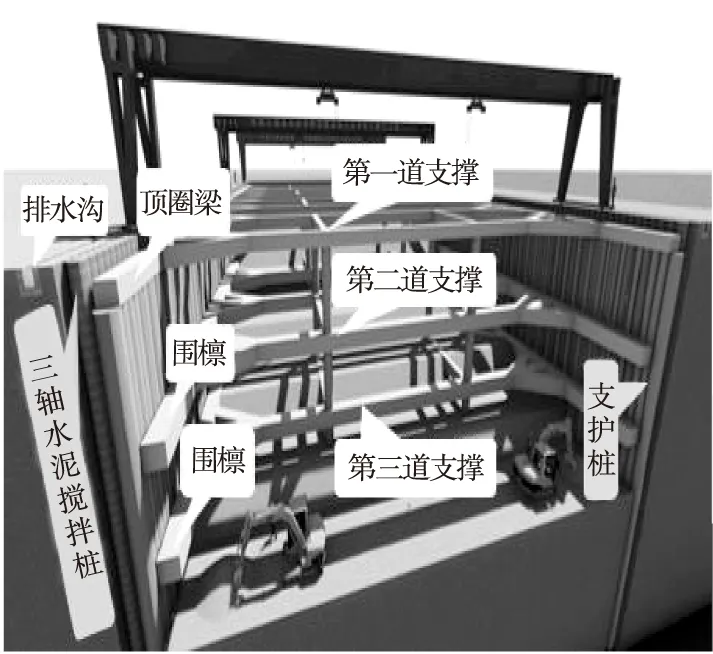
图3 基坑支护结构BIM模型Fig.3 BIM model of foundation pit supporting structure

3 优化模型设计

3.1 数学模型描述

填海地区深基坑支护结构优化设计模型用数学语言可描述为[10]

(1)

式中:x1，x2,…,xn为变量;n为变量数量;m为约束数量。

3.2 优化变量选择

将影响大、不易被设计人员确定的参数作为优化变量。为此以支护桩的最大位移为关键指标,利用理正深基坑支护计算软件对桩径D、嵌固深度hd、桩距S及支撑深度m做敏感性分析,结果如图4～图7所示。

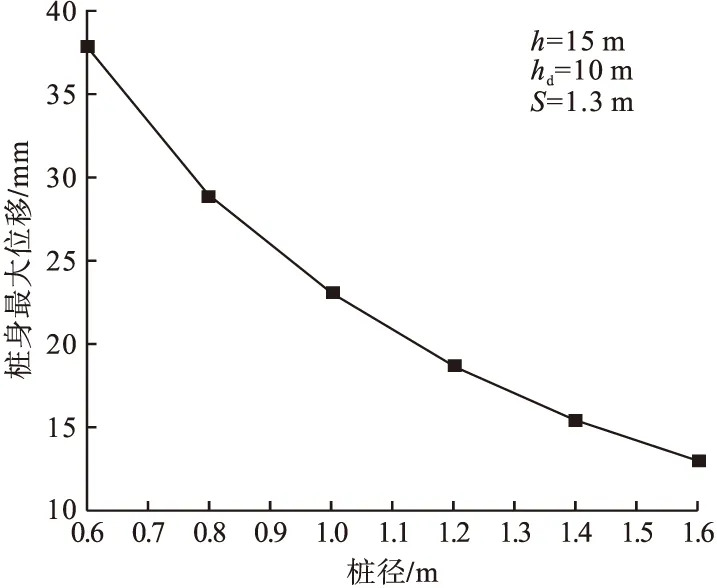
图4 桩身最大位移随桩径变化曲线Fig.4 The changing curve of maximum displacement of pile with pile diameter

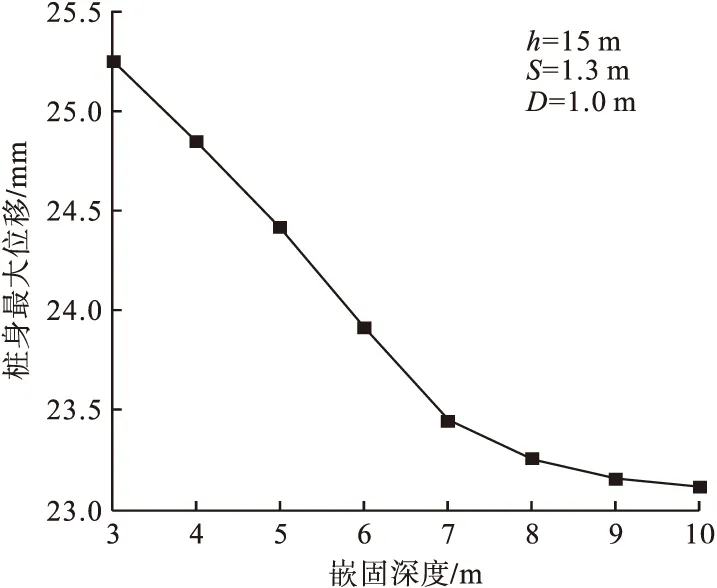
图5 桩身最大位移随嵌固深度变化曲线Fig.5 The changing curve of maximum displacement of pile with embedded depth

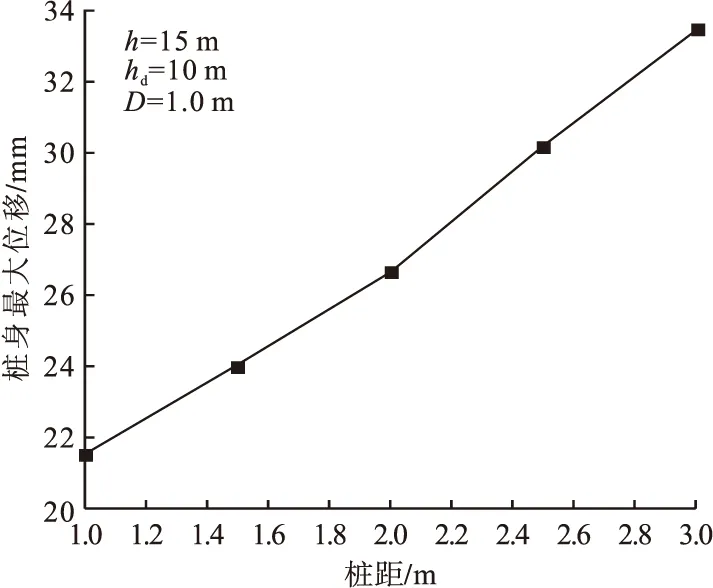
图6 桩身最大位移随桩间距变化曲线Fig.6 The changing curve of maximum displacement of pile with pile spacing

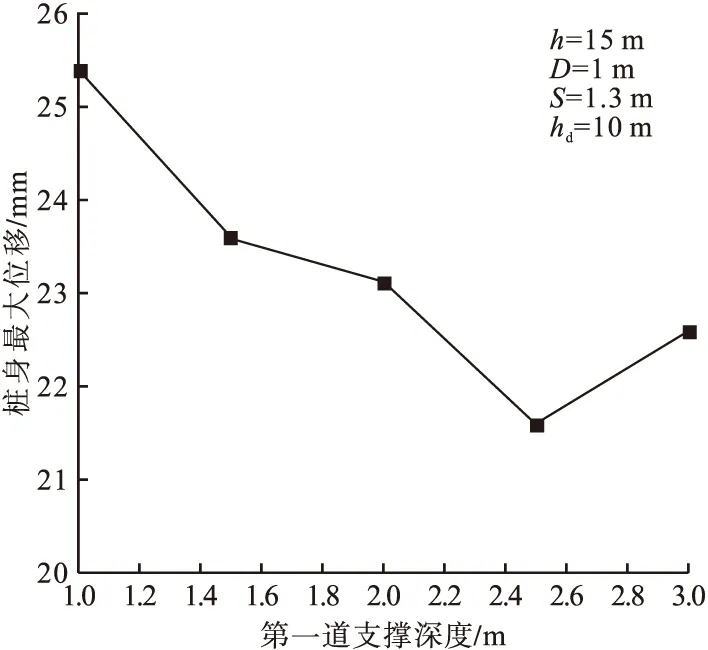
图7 桩身最大位移随第一道支撑深度变化曲线Fig.7 The changing curve of maximum displacement of pile with the first supporting depth

对敏感性分析结果可知,桩身最大位移在一定范围内随桩径、嵌固深度较剧烈变化,超过某临界点时,变化幅度变缓,甚至保持不变。从图4可以看出,桩径超过0.9 m时,桩身最大位移的减少幅度放缓;从图5可以看出,桩体嵌固深度超过9 m时,桩体最大位移基本不再改变,保持在23.16 mm;从图6可以看出,桩身最大位移随着桩距增大而增大,主要是由于桩与桩之间的相互约束作用减弱;从图7可以看出,桩身最大位移随着第一道支撑深度增大呈现先减小后增大的趋势:当第一道支撑深度介于1～2.5 m时,由于随着第一道支撑与第二道支撑距离的接近,对桩身约束作用明显加强;但当第一道支撑深度超过2.5 m,会对桩顶位移约束不足,造成最大位移重新增大。因此,合理选择设计参数对基坑支护结构安全性有着显著影响。

3.3 目标函数确定

为降低优化难度,利用BIM技术的工程量统计功能预先固定混凝土内支撑的施工造价以及其他次要造价,在优化过程中暂不考虑。故最终以桩体自身的材料造价作为目标函数:

(2)

式中:D为桩径;hd为桩嵌固深度;S为桩距;h为基坑深度;Cc为每方混凝土造价;L为基坑周长;λs为钢筋密度,一般取7.85 t/m3;As为纵向钢筋总截面面积;Cs为每吨钢筋造价。m为3道支撑深度,虽未直接体现在表达式中,但其取值不同会让桩身的受力状态随之改变,对桩径和嵌固深度产生影响,进而对目标函数及约束条件产生影响。

由于桩身位移与基坑支护结构安全息息相关,结合敏感性分析结果最终选取优化变量:桩径、嵌固深度、桩距及支撑深度。同时结合规范、地质条件、BIM模型等将能够明确或者影响较小的参数作为预知变量预先确定下来,如混凝土强度等级、内支撑截面尺寸、钢筋等级、支撑道数等。

3.4 约束条件确立

为保证填海地区深基坑支护结构的安全性和稳定性,在进行优化时必须满足一定约束条件,通常分为变量自身约束、变量耦合约束和设计准则约束三类[11]。

(1)变量自身约束

依据《建筑基坑支护技术规程》(JGJ 120—2012)和《深圳市基坑支护技术规程》(SJG 05—2011)等规范,可确定优化变量自身取值区间,得到支护结构参数范围。

①旋挖钻孔桩径D取值范围:D=[0.6,1.8];

②桩距S取值范围:S=[D,2D];

③多点支撑嵌固深度hd取值范围:hd=[0.2h,0.6h];

④第一道支撑深度m1[0.1h,0.5h];第二道支撑深度m2(m1，h);第三道支撑深度m3(m2，h)。

(2)变量耦合约束

变量耦合约束是指各优化参数之间相互影响、相互约束。根据文献[12-14]确定变量耦合约束条件如下。

①桩间距最大值。为确保土层自平衡,桩间距应符合式(3):

(3)

式中:θ=45°+ψ/2,ψ为内摩擦角;D为桩径。

②嵌固深度最小值。对于多点支撑结构来说,嵌固深度应满足式(4):

g2(D,hd,S,m)=hdmin-hd=0.2h-hd≤0.

(4)

式中:hdmin为最小嵌固深度;h为基坑深度。

(3)设计准则约束

设计准则约束指优化参数必须符合相关设计标准所规定的内力、变形约束。

①内力约束。为保证支护桩不发生破坏,桩身的最大弯矩应满足式(5):

g3(D,hd,S,m)=M-Mmax≤0.

(5)

式中:M为桩身承受弯矩；Mmax为桩身承受的最大弯矩。

②变形约束。填海地区深基坑支护结构的变形应符合式(6):

g4(D,hd,S,m)=δ-[δ]≤0.

(6)

式中:δ为桩身位移;[δ]为桩允许位移限值,取0.002h与30 mm的较小值。

4 优化模型的算法实现

4.1 编码及种群初始化

编码是运用遗传算法解决问题的关键,目前运用较为广泛的编码方式有二进制编码、浮点编码、多参数交叉编码等[15]。为平衡计算精度与算法收敛速度的矛盾,笔者采用二进制来表达染色体上的基因。种群初始化即在遗传搜索空间里均匀随机产生N个长度为Q的染色体,N取决于种群个体数,Q与计算精度、变量数、编码方式有关。

4.2 适应度函数变换

在填海深基坑支护结构优化问题中,需对各种繁多约束条件进行处理,采用惩罚函数来构造适应度函数,使原来受约束的非线性优化问题转化为无约束的非线性优化问题[16]。通过变换目标函数,将适应度函数定义为

(7)

式中:F(x)表示目标函数;c一般与违背约束条件的影响有关,文中取12;如果满足约束条件,则gj(x)取值为0,否则取为极大正参数T,表示对可行域外的目标函数值进行惩罚。

4.3 遗传算子设计及迭代终止

(1)选择算子

选择是遗传算法优化的内在驱动力,通过淘汰种群中适应值小的个体来促进种群的进化。基于此,利用轮盘赌来确定选择算子,具体步骤如下[17]。

①计算染色体选择概率pi及累计概率qk:

(8)

(9)

②确定新种群。在区间[0,1]随机产生一个随机数r,若r≤q1,则选择第1条染色体;否则寻求使qk-1

(2)交叉、变异算子

设计交叉、变异算子是新个体产生的主要途径,直接决定算法的求解效率及全局搜索能力。为减小运行过程中陷入局部最优解的机率,引入动态自适应技术对交叉、变异算子进行改进,让其按照式(10)、式(11)分别进行自适应变化[18]:

(10)

(11)

式中:Pc、Pm分别为交叉概率和变异概率;Pc1、Pc2分别为交叉算子的上下限;Pm1、Pm2分别为变异算子的上下限;f′表示两两交叉个体中较大的适应度值;f表示变异个体的适应度值;favg表示种群平均适应度值,fmax表示种群最大适应度值。

(3)迭代终止

经过选择、交叉、变异操作形成新种群,判断新种群的favg、fmax是否满足式(12):

(12)

式中:ε为预先设定的精度,文中取10-4。若满足收敛条件或运行到指定代数时迭代终止,输出此时fmax对应的可行解X0=[D,S,hd,m]即为最佳优化参数。

4.4 计算结果分析

基于BIM模型,首先获取妈湾跨海通道基坑支护结构优化的基本参数,将其代入到优化模型中,并利用遗传算法在Matlab软件中编程求解。在初始种群为20的情况下,经50代左右收敛,此时各优化变量达到最佳,结果见表2。

表2 优化结果与原设计比较Table 2 Comparison of optimization results with the original design

从表2可以看出,在桩径基本不变的情况下,桩距、嵌固深度都较原设计有不同程度的减低,与敏感性分析结果基本一致。对桩径、桩距、嵌固深度及支撑深度的优化调整,不仅可以节省材料造价,还能改善桩身的内力。在满足内力与变形约束的前提下,材料造价由原来的4 345万元降到4 162万元,造价降低了4%,经济效果明显。如图8所示,将优化后的参数代入理正深基坑软件计算可知,优化后的支撑深度也更加合理,随着支撑深度一定程度的下移,桩身的最大弯矩也得到改善,从880.42 kN·m降到756.97 kN·m,降低了14%。将表2中优化后参数重新输入到模型中,利用参数化建模方式即可完成填海地区深基坑支护结构BIM模型的自动化生成,模型如图9所示。