双母线直流微电网的级联稳定性分析

2021-05-18杜明桥张伟亮陈守克

电力自动化设备 2021年5期

张辉，杜明桥，孙凯，张伟亮，陈守克

（1. 西安理工大学电气工程学院，陕西西安710048；2. 清华大学电力系统及发电设备控制和仿真国家重点实验室，北京100084）

0 引言

直流微电网因光伏等可再生能源的安装与运维成本逐渐降低、居民用电安全诉求提升以及直流负载数量日益增加，而逐渐成为居民建筑和家居、数据中心等领域的主要供电架构［1-2］。随着更高效、可持续能源体系的不断完善，且单母线直流微电网具有工作容量有限、抗扰能力弱等问题［3］，采用双有源桥DAB（Dual Active Bridge）变换器连接各条母线，形成双母线、多母线等的拓扑结构［4］被提出，进而带来一些新的问题：①建立系统完整小信号模型以及分析其稳定性的难度增大；②母线间功率交互导致功率振荡和变换器阻抗特性改变［5］；③多种变换器（包括DAB变换器［6］）接入直流微电网，造成级联变换器之间相互作用，或与滤波器参数发生谐振，降低了系统的稳定性［7］。因此，研究双母线、多母线直流微电网的小信号建模和稳定性对系统的稳定运行具有重要的意义。

目前，有关单母线直流微电网稳定性分析方面的研究已较为成熟［8-10］，从传统的直流微电网稳定性分析方法（如时域特征值分析法、频域Nyquist 判据），发展至具有无需源荷系统内部参数、保守性适当、适用于复杂微电网等特点的阻抗分析方法（如Middlebrook 判据［11］以及幅值相角裕度GMPM（Gain Margin and Phase Margin）判据［12］）。而在双母线、多母线直流微电网的小信号稳定性方面，大多研究从小信号建模和特征值分析的角度讨论了控制环、负载供电稳定性和微电网稳定性。文献［13］建立了双母线直流微电网的小信号模型，基于特征值分析电池荷电状态、恒功率负载和线路阻抗对系统稳定性的影响；文献［14-15］在多母线直流微电网的柔性互联控制和协调功率控制下，给出了系统完整的通用小信号模型，并基于系统特征值分析发生阶跃扰动时母线电压的动态性和稳定性；文献［16-17］给出了双母线直流微电网在不同工况下的小信号模型，利用特征值分析法分析控制参数和滤波参数对系统稳定性的影响，达到了优化系统参数的目的；文献［18］为了采用基于阻抗的稳定性判据，将多母线直流微电网划分为单母线直流微电网，并提出了简化小信号模型，即利用特征值分析系统的低频稳定性；文献［19］针对含光伏的多母线微电网，建立了光伏微电网系统的详细小信号模型，揭示了相邻母线之间会产生超低频振荡和中低频局部振荡，母线间的相互作用还会降低系统阻尼，从而导致系统不稳定。

综上所述，有关微电网小信号稳定性的研究大多集中在控制策略的稳定性和单母线直流微电网中变换器与负荷的级联问题，而对于包含DAB 变换器的双母线、多母线结构的相关研究较少。为此，本文重点研究了双母线直流微电网在多种运行模式下的建模、阻抗特性分析以及系统负荷供电稳定性。首先，从阻抗分析角度出发，依据系统在不同运行模式下各变换器的源荷属性提出4 种阻抗模型，分析系统输入／输出阻抗伯德图及阻抗比Nyquist 曲线，研究不同运行模式、微源和负载阻抗特性对微电网小信号稳定性的影响；然后，对比3 种无源方案以提高系统的负载供电稳定性；最后，通过仿真和实验验证理论分析的正确性。

1 双母线直流微电网的等效阻抗模型

双母线直流微电网的拓扑结构见图1。直流母线1、2 分别为低压侧、高压侧母线（含并网接口），子网1、2 都包含光伏单元、储能单元和负载单元，其中光伏单元采用Boost 变换器，储能单元采用Buck／Boost 变换器，子网间隔离型DC／DC 互联变换器采用DAB变换器。

图1 双母线直流微电网的拓扑结构Fig.1 Topology structure of double-bus DC microgrid

1.1 隔离型DC／DC互联变换器阻抗模型

隔离型DC／DC 互联变换器采用DAB 变换器，其拓扑结构见图2。图中，C1、C2为两侧直流母线电容；Rs为线路等效电阻；L、RL分别为辅助电感及其等效电阻；iL为辅助电感电流；udc1、iin分别为母线1 的直流侧电压、变换器输入电流；udc2、io分别为母线2的直流侧电压、变换器输出电流；uC1、uC2分别为C1、C2的电压；n1∶n2为变压器T的匝数比。

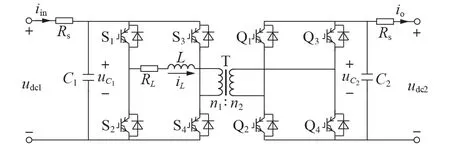
图2 DAB变换器的拓扑结构Fig.2 Topology structure of DAB converter

DAB变换器在传统单移相控制的基础上增加了柔性功率控制和恒压控制，分别用于实现两侧储能单元和光伏单元柔性功率分配与电压支撑。DAB变换器的电压控制和功率控制框图见附录中图A1。图中，Ppv1、Ppv2分别为子网1、2 中光伏单元的输出功率；kpv1、kpv2分别为子网1、2 中光伏单元容量的比例系数；Pdcb1、Pdcb2分别为子网1、2 中储能单元的输出功率；kb1、kb2分别为子网1、2中储能单元容量的比例系数。需要指出的是，稳态运行时母线电压由储能单元支撑，为了满足各储能出力均衡以及研究稳态模式的需要，本节建立了DAB 变换器柔性功率控制的闭环阻抗模型。

因传统状态空间平均建模法仅适用于状态变量扰动频率远低于开关频率的情况，不适用于具有高频状态变量的场景［20］，如DAB 变换器中高频变压器侧电感电流状态变量在一个开关周期内的平均值为0［21］。为此，本文采用广义状态空间建模法（GAM）对辅助电感电流进行一次和二次傅里叶分解［21］，使DAB 变换器的等效阻抗模型更精确。根据图2 建立DAB变换器的状态空间方程如式（1）所示。

其中，x k(t)为傅里叶级数中的第k次谐波系数；ωs为开关的角频率（rad／s）；T= 1/fs为开关周期，fs为开关频率（Hz）。

因此，将DAB 变换器的状态变量uC1、uC2、iL代入式（2）和式（3），得到傅里叶分解后的广义状态空间方程为：

其中，ΔxOL、ΔuOL、ΔyOL分别为经傅里叶分解后的状态变量小扰动值、输入变量小扰动值、输出变量小扰动值列向量；AOL、BOL、COL、DOL为广义状态矩阵的系数矩阵［21］。

根据状态方程式（4）和DAB 变换器的控制框图建立其闭环小信号模型控制框图，如图3 所示。图中，GiRd_DAB、GiRi1_DAB、GiRi2_DAB分别为移相角小扰动值Δd、变换器输入电流小扰动值Δiin、输出电流小扰动值Δio到电感基波电流小扰动值ΔiL_1R的传递函数；GiId_DAB、GiIi1_DAB、GiIi2_DAB分别为Δd、Δiin、Δio到电感2 次谐波电流小扰动值ΔiL_1I的传递函数；Gv1d_DAB、Gvli2_DAB分别为Δd、Δio到母线1的直流侧电压小扰动值Δudc1的传递函数；Zoin_DAB为Δiin到Δudc1的传递函数（即开环输入阻抗）；Gv2d_DAB、Gv2i1_DAB分别为Δd、Δiin到母线2 的直流侧电压小扰动值Δudc2的传递函数；Zoout_DAB为Δio到Δudc2的传递函数（即开环输出阻抗）。

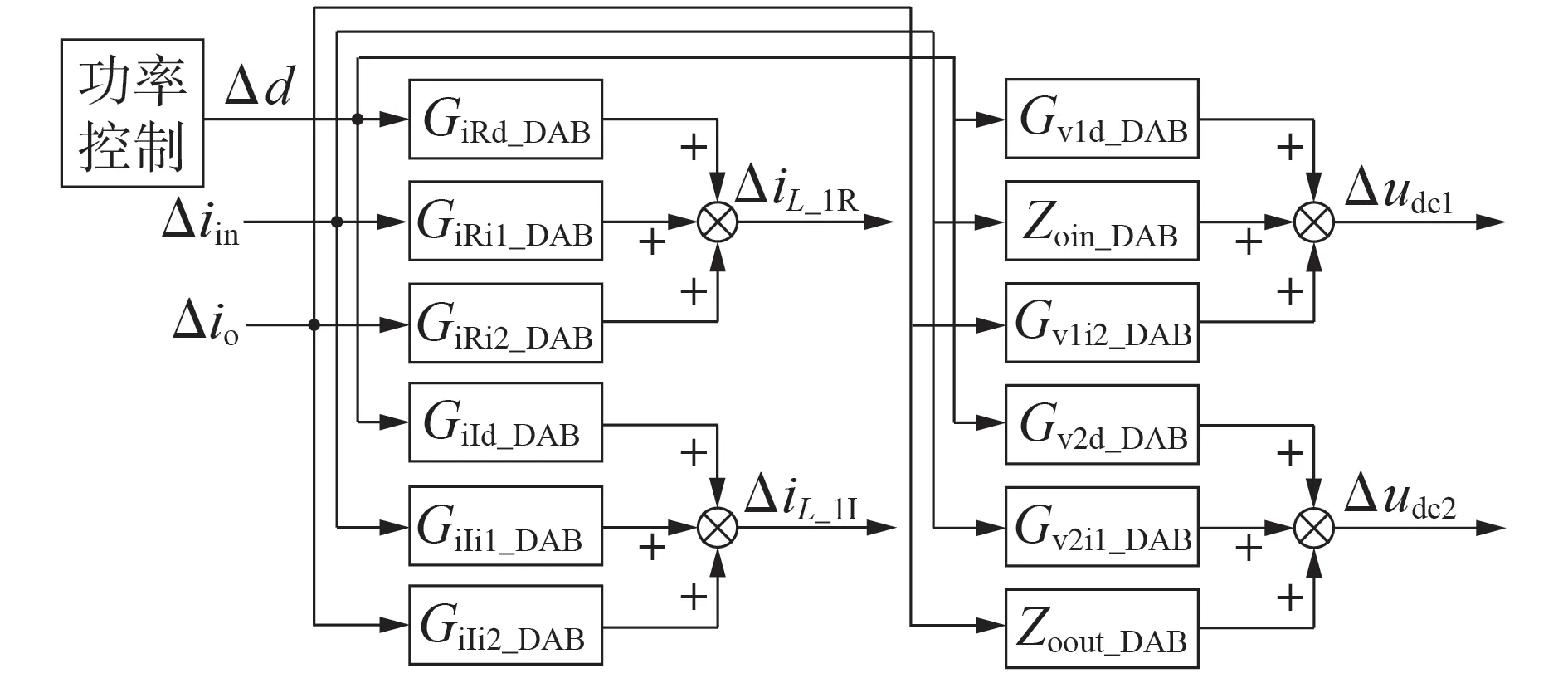
图3 DAB变换器的闭环小信号模型控制框图Fig.3 Control block diagram of closed-loop smallsignal model for DAB converter

由图3可得到功率控制下DAB 变换器的闭环输入阻抗Zcin_DAB和闭环输出阻抗Zcout_DAB分别为：

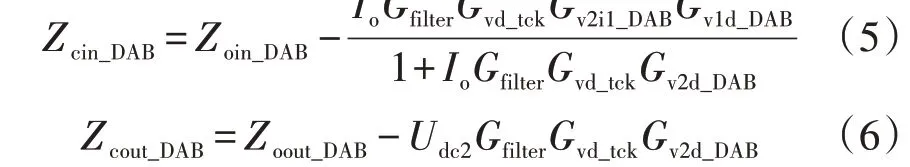
其中，Io、Udc2分别为DAB 变换器输出电流io、母线2直流侧电压udc2的稳态值；Gvd_tck为功率环PI 控制器的传递函数；Gfilter为低通滤波器的传递函数。

DAB变换器采用功率控制实现母线间的功率交换，可看作恒功率微源，即可等效为电流源并联电阻的诺顿等效模型。

1.2 光伏单元Boost变换器的阻抗模型

基于文献［14］中的开环输出阻抗表达式，并加入最大功率点跟踪（MPPT）控制，得到光伏单元MPPT 控制框图见附录中图A2。图中，upv、ipv分别为光伏单元的端口电压、输出电流；dpv为Boost 变换器开关的占空比。则加入MPPT控制后光伏单元Boost变换器的闭环输出阻抗Zcpv为：

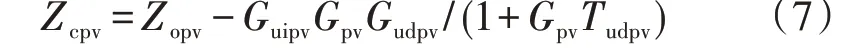
其中，Zopv为Boost 变换器的开环输出阻抗；Gudpv为Boost变换器移相角到母线电压的传递函数；Gpv为电压PI控制器的传递函数；Tudpv、Guipv分别为Boost变换器占空比、变换器输出电流到光伏单元端电压的传递函数。

Boost 变换器采用MPPT 控制实现最大功率输出，可看作恒功率微源，即可等效为电流源并联电阻的诺顿等效模型。

1.3 储能单元Buck／Boost变换器的阻抗模型

基于文献［15］中的开环输出阻抗表达式，并加入下垂控制，得到储能单元下垂控制框图见附录中图A3。图中，udcb、idcb分别为储能单元的输出电压、电流；iLb为电感电流；db为储能单元Buck／Boost 变换器开关的占空比。则加入下垂控制后储能单元的放电输出阻抗Zcout_b、充电输入阻抗Zcin_b分别为：

其中，Zob为储能单元的开环输出阻抗；kb为储能单元的下垂控制系数；Gic为电流闭环传递函数；Gud为移相角到母线电压的传递函数；Gii为变换器输出电流到电感电流的传递函数；Gbu、Gbi分别为电压PI 控制器、电流PI控制器的传递函数。

储能单元Buck／Boost 变换器采用下垂控制维持母线电压的微源变换器，可等效为电压源串联电阻的戴维南等效模型。

1.4 双母线直流微电网的级联形式与切换条件

图4 4种模式的等效阻抗模型Fig.4 Equivalent impedance models of four modes

根据系统中各单元输出、吸收功率的状态，划分其属于微源侧还是负载侧，光伏单元输出功率，则将其划分为微源侧；储能单元、DAB变换器和负载单元吸收功率，则将其划分为负载侧。由此提出如下4种模式，每种模式对应一种级联形式。4 种模式的等效阻抗模型见图4。图中，ubus为母线电压，其左侧、右侧分别为微源侧和负载侧；Ls、Cs、Rload分别为滤波电感、滤波电容、负载电阻，三者组成了负载单元阻抗Zload；idcpv1、icp1、iload分别为光伏单元输出电流、DAB 变换器输入电流、负载电流。4 种模式的微源侧总输出阻抗Zso和负载侧总输入阻抗ZLi见附录中表A1。

（1）模式1：光伏单元输出功率，储能单元充电，子网1 通过DAB 变换器向子网2 输送功率，负载单元吸收功率。

（2）模式2：光伏单元输出功率，储能单元放电，子网1 通过DAB 变换器向子网2 输送功率，负载单元吸收功率。

（3）模式3：光伏单元输出功率，储能单元充电，子网2 通过DAB 变换器向子网1 输送功率，负载单元吸收功率。

（4）模式4：光伏单元输出功率，储能单元放电，通过DAB变换器向，负载单元吸收功率。

然后分析4 种模式的切换条件。模式1—4 之间的差异是由储能单元的充放电状态和DAB 变换器的功率传输方向造成的。因此，关于模式之间的切换条件，一方面是子网1、2 负载总容量的增减（如子网1、2 同时增加同容量负载使储能单元从充电状态逐渐过渡到放电状态）；另一方面是子网1、2 的负载不平衡度增减（如仅子网2 减载，引起子网2 功率冗余，DAB变换器的功率传输方向由子网1向子网2传输逐渐切换为由子网2向子网1传输）。需要指出的是，只有满足切换条件以及一定的负载变化，才会进行模式切换，否则认为仍处于同一模式。4 种模式的切换过程如下。

（1）设定初始状态为子网1与子网2的负载容量相等且总容量为轻载情况，当子网2 的负载增加时，负载不平衡度增加，子网1通过DAB变换器向子网2传输一定的功率。此时对于子网1 而言，其光伏单元输出功率，储能单元充电，DAB 变换器吸收功率，处于模式1。

（2）在保持模式1 负载平衡度不变的情况下，两侧负载同时逐渐增加相同容量，则总容量逐渐增加，储能单元从吸收功率逐渐过渡到输出功率。此时对于子网1 而言，其光伏单元输出功率，储能单元放电，DAB变换器吸收功率，处于模式2。

（3）在模式2 的条件（子网1、2 的负载不平衡且总容量为重载情况）下，子网2 的负载逐渐降低，DAB 变换器向子网2 输送的功率逐渐下降，直至达到0，但此时仍处于模式2 下。当子网2 的负载再次降低时，负载总容量也逐渐降低，储能单元逐渐从输出功率逐渐过渡到吸收功率，到达稳态点。此时对于子网1 而言，其光伏单元输出功率，储能单元充电，DAB变换器向负载输出功率，处于模式3。

（4）在模式3 的条件（子网1、2 的负载不平衡且总容量为轻载情况）下，子网1、2 的负载同时增加相同容量，负载平衡度不变，DAB变换器传输的功率不变，而负载总容量增加，则储能单元从吸收功率逐渐过渡到输出功率，到达稳态点。此时对于子网1 而言，其光伏单元输出功率，储能单元放电，DAB 变换器向负载输出功率，处于模式4。

由上述分析可知，系统中负载总容量大小、子网间的负载平衡度变化都会导致储能单元、DAB 变换器被划分为微源侧或负载侧，从而形成4 种模式，下文将对这4种模式下的级联形式进行阻抗分析。

2 级联小信号稳定性分析

2.1 微电网在4种模式下的输出、输入阻抗分析

结合各变换器的工作模式，针对上述4 种模式在不同稳态点进行小信号稳定性分析。双母线直流微电网的4 种模式在稳态工作点处各微源输出阻抗和负载输入阻抗伯德图见附录中图A4，具体分析如下。

（1）模式1的输出、输入阻抗伯德图见图A4（a），总输出阻抗由基于MPPT 控制的光伏单元构成，在低频段的相位为-180°，呈现负阻抗特性；总输入阻抗由基于下垂控制的储能单元、基于功率控制的DAB 变换器和负载单元构成，其中储能单元的输入阻抗幅值在低频段时最小且相位为-180°，总输入阻抗特性与储能单元类似，呈现负阻抗特性。随着角频率增加以及受LC滤波器影响，总输出阻抗幅值下降且相位由-180°增加至0°，逐渐从负阻抗特性改变为纯阻性；总输入阻抗幅值在200 rad／s 角频率附近出现负谐振尖峰且阻抗特性由容性变为感性。

（2）模式2的输出、输入阻抗伯德图见图A4（b），总输出阻抗由储能单元和光伏单元构成，储能单元的输出阻抗幅值在低频段最小，光伏单元的输出阻抗幅值在高频段最小，总输出阻抗特性在低频段与光伏单元类似，在高频段与储能单元类似，均呈现纯阻性；总输入阻抗由DAB 变换器和负载单元构成，负载单元的输入阻抗幅值在低频段最小且相位为0°，因此总输入阻抗特性在低频段与负载单元类似，呈现纯阻性。随着角频率增加以及受LC 滤波器影响，模式2 在200 rad／s 角频率附近的波形与模式1相似但负谐振尖峰较弱。

（3）模式3的输出、输入阻抗伯德图见图A4（c），总输出阻抗由光伏单元和DAB 变换器构成，呈现恒功率特性，光伏单元的输出阻抗幅值全频段最小，总输出阻抗特性在低频段与光伏单元类似，呈现负阻抗特性；总输入阻抗由储能单元和负载单元构成，其中储能单元的输入阻抗幅值在低频段最小且相位为-180°，总输入阻抗特性在低频段与储能单元类似，呈现负阻抗特性。随着角频率增加以及受LC滤波器影响，总输出阻抗特性与模式1 类似，但整体幅值更小；总输入阻抗特性与模式2 类似，但负谐振尖峰更大。

（4）模式4的输出、输入阻抗伯德图见图A4（d），总输出阻抗由光伏单元、DAB 变换器和储能单元构成，储能单元的输出阻抗幅值在低频段最小，光伏单元的输出阻抗幅值在高频段最小，总输出阻抗特性在低频段与储能单元类似，在高频段与光伏单元类似，全频段均呈现纯阻性，变化趋势与模式2 类似，但整体幅值更小，即级联系统更稳定；总输入阻抗由负载单元构成，其阻抗特性由负载单元决定，呈现纯阻性。

根据上述分析可知，在较低频段且光伏单元采用MPPT 控制、储能单元采用下垂控制以及DAB 变换器采用柔性功率控制时，光伏单元作为微源呈现负阻抗特性；储能单元作为微源时，其阻抗幅值最小，相位为0°，而作为负载时，其相位为-180°，呈现负阻抗特性；DAB变换器无论是作为微源还是负载，其阻抗幅值都最大，且相位均为-180°，呈现负阻抗特性。因此，根据GMPM 判据［12］，双母线直流微电网稳定性的优劣主要由基于MPPT 控制的光伏单元的放电状态、基于功率控制的DAB 变换器的充放电状态、基于下垂控制的储能单元的充电状态以及负载侧输入LC滤波器决定。

2.2 微电网总输出、输入阻抗分析

双母线直流微电网在4 种模式下的总输出阻抗Zso、总输入阻抗ZLi伯德图分别见图5（a）、（b），阻抗比Zso/ZLi的Nyquist 曲线及其局部放大图分别见图5（c）、（d）。由图可知，全频段内模式1 的总输出阻抗幅值最大，总输入阻抗幅值最小；各模式下的阻抗比都在禁止区之外，与禁止区的距离由近及远依次为模式1、3、2、4。

根据GMPM 判据［12］可知，各模式下小信号模型均稳定，并能保证6 dB 幅值裕量和60°相位裕量。其中，模式4的稳定性最高，模式1的稳定裕量最小，抗扰能力最差，故本文选取模式1 的稳定性指标作为系统稳定性指标。

2.3 无源阻抗方案

2.3.1 无源阻抗方案的选取依据

由2.1 节可知双母线直流微电网稳定性的主要影响因素是输入侧LC 滤波器和恒功率单元的负阻抗特性。且LC 滤波器、储能单元和DAB 变换器的输入阻抗相互作用，会导致系统在输入侧产生负谐振尖峰。因此，可通过增加无源或有源阻抗的方法来提高总输入阻抗，以降低负谐振尖峰的影响，从而提高系统的稳定性［8，10］。

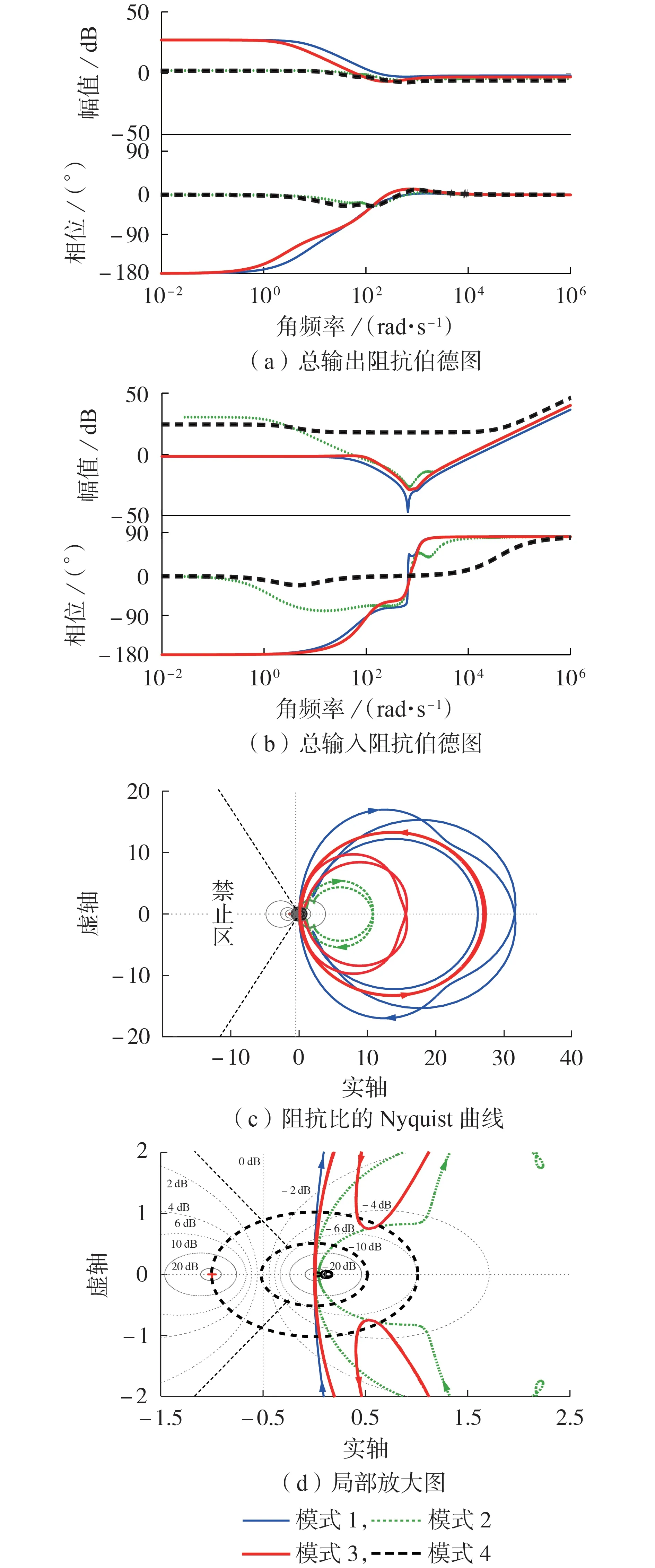
图5 4种模式下的总输出阻抗、总输入阻抗伯德图及阻抗比Nyquist曲线Fig.5 Bode diagrams of total output impedance and total input impedance and Nyquist curves of impedance ratio under four modes

本文选取无源阻抗方案，主要原因如下：①有源阻抗方案需要增加一定的控制回路，这会增加控制复杂度和阻抗建模复杂度，从而影响阻抗分析的准确性；②双母线直流微电网中基于下垂控制的储能单元的输出阻抗在低频段可等效为下垂系数，采用有源阻抗方案改变输出阻抗意味着改变下垂系数，这会影响储能单元的输出功率均分［10］；③无源阻抗方案无需额外的软件，实现简单，其损耗能够通过选取合适阻值大小而维持在合理的范围内。

基于文献［22］中的3 种无源阻抗方案，给出加入无源阻抗后模式1的等效阻抗模型如附录中图A5所示，其负载输入阻抗伯德图如附录中图A6 所示。图A6中，Cs1、Rs1分别为无源阻抗方案1的并联电容、电阻；Ls2、Rs2分别为无源阻抗方案2 的并联电感、电阻；Rs3为无源阻抗方案3 的串联电阻。无源阻抗方案1 设定Rs1=8 Ω，随着Cs1增加，谐振尖峰处负载输入阻抗幅值从-22 dB 改善至-9.4 dB，改善效果小且存在一定的相位偏差；无源阻抗方案2 设定Rs2=8 Ω，随着Ls2增加，谐振尖峰处负载输入阻抗幅值显著提高，但在低频段的阻抗幅值为电感幅值，会产生较大的功率偏差；无源阻抗方案3，随着Rs3增加，谐振尖峰处负载输入阻抗幅值显著提高，负谐振尖峰逐渐消失且低频段的幅值不受阻抗参数影响。综上，本文选取无源阻抗方案3 用于减小输入阻抗负谐振尖峰的影响。

2.3.2 加入无源阻抗后的稳定性分析

以工作在模式1的子网1为例，分析加入无源阻抗方案3 后系统的稳定性，结果见图6。由图可知，当Rs3=0 时，总输入阻抗在645 rad／s 角频率处存在-47 dB 的负谐振尖峰；随着Rs3增大（从0 增大至14 Ω），总输入阻抗幅值增大（负谐振峰值由-47 dB改善至-9.5 dB），直流微电网的稳定性提高，但Rs3过大会增加损耗，因此应合理选取Rs3的大小。设滤波参数Cs=100 μF，Ls=0.2 mH 不变，随着Rs3增大（从0增大至8 Ω），阻抗比的幅值裕量不变，相位裕量由91.3°增加至102.5°，其Nyquist 曲线逐渐远离禁止区，双母线直流微电网的稳定性得到提高。

由上述分析可知，无源阻抗方案3 能够改善负载输入阻抗特性，从而提高系统稳定性，且在一定的范围内，阻值越大则越能改善负谐振尖峰幅值，但增大到一定程度后，改善效果将减弱。因此，综合考虑损耗和改善效果，本文选择Rs3=8 Ω 作为后续的仿真与实验参数。

3 仿真与实验验证

在MATLAB 平台上搭建图1 所示双母线微电网的仿真模型，验证子网1、2母线电压为1∶1时系统的小信号稳定性和无源阻抗方案的有效性。仿真参数见附录中表A2。规定子网1 通过DAB 变换器向子网2 输送的功率为DAB 变换器功率正方向，即DAB变换器功率为5 kW 表示子网1 通过DAB 变换器向子网2 输送5 kW 功率（子网2 通过DAB 变换器向子网1 吸收5 kW 功率）。因稳态运行模式下母线电压恒定，则电流值与功率值基本一致，下文采用电流值表述各单元的功率交互情况。

图6 加入无源阻抗方案3后模式1的仿真结果Fig.6 Simulative results of Mode 1 after adding passive impedance scheme 3

对子网1 和子网2 进行加、减载以验证2.2 节中4 种模式的小信号稳定性，仿真结果见图7（a）、（b）。加入无源阻抗（Rs3=8 Ω）后的仿真结果见图7（c）。加入无源阻抗前、后的母线电压相同。图中，下标1、2分别表示子网1、2；idab为DAB变换器输出电流。

图7 加入无源阻抗前、后的电流波形和母线电压波形Fig.7 Current waveforms and bus voltage waveforms before and after adding passive impedance

由图7（a）、（b）可得如下结论。

（1）0.5 s 时，子网1 与子网2 通过DAB 变换器互联，在（0.5，2）s 时段内，子网1、2 的负载功率分别为9.9、10.10 kW（负载功率平衡），子网1、2光伏单元的输出功率均为19.99 kW，子网1、2 储能单元充电功率均为9.98 kW，DAB变换器输出功率为0。

（2）1 s 时，子网2 负载功率突增至20.10 kW（子网1 与子网2 的负载功率不平衡），经过0.15 s 调节时间后，子网1、2 分别切换至模式1、3。子网1、2 光伏单元的输出功率均为20.1 kW，子网1、2 储能单元充电功率均为5.13 kW，DAB 变换器的输出功率为5.13 kW。模式1下负载电流为13.90 A，纹波系数为14.3%。

（3）1.5 s 时，子网1、2 的负载分别突增至19.98、29.76 kW，经过0.2 s 调节时间后，子网1、2 分别切换至模式2、4。子网1、2 光伏单元的最大输出功率分别为20.10、19.82 kW，子网1、2储能单元的放电功率和DAB 变换器输出功率均为4.91 kW。模式2 下负载电流为28.92 A，纹波系数为5.1%。

（4）2 s 时，子网2 减载至10.10 kW，经过0.2 s 调节时间后，子网1、2 分别切换至模式3、1。子网1、2光伏单元的输出功率分别为20.15、19.85 kW，子网1、2 储能单元的放电功率和DAB 变换器输出功率均为4.95 kW。模式3下负载电流为28.22 A，纹波系数为7.7%。

（5）2.5 s时，子网1、2负载分别变为30、20.10 kW，经过0.25 s 调节时间后，子网1、2 分别切换至模式4、2。子网1、2 光伏单元的输出功率分别为20.25、20.10 kW，子网1、2 储能单元的放电功率均为4.99 kW，DAB 变换器输出功率为-4.99 kW。模式4下负载电流为43.43 A，纹波系数为2.3%。

上述仿真结果验证了功率控制策略的有效性：①任一个子网功率发生突变时都可通过DAB 变换器维持功率均衡，实现子网1、2 中储能单元的功率均分；②功率控制策略能保证2 条母线的电压成恒比例（1∶1）关系。同时上述结果也验证了4 种模式下的小信号稳定性：①系统在4 种模式下均能保证小信号稳定；②子网1 和子网2 在模式1 下的负载电流纹波最大，抗扰性能最差，在模式4 下的负载电流纹波最小，抗扰性能最好，与2.2 节的阻抗分析结果一致。

由图7（b）、（c）可知：相比于加入无源阻抗前，加入无源阻抗后光伏单元、储能单元的电流波形和母线电压波形没有明显变化，但负载电流纹波减小；子网1 在模式1 下的负载电流纹波系数由14.3%降低至1.9%。可见，无源阻抗在保证子网1、2 中微源输出功率和母线电压不变的情况下，可有效抑制因LC滤波器、储能单元和DAB 变换器间相互作用所产生的负谐振尖峰，增强了LC滤波器对负载电流的滤波效果，提高了子网1、2 对负载的供电稳定性，与2.3节的阻抗分析结果一致。

为了进一步验证子网1、2 母线电压比为1∶2 时系统的小信号稳定性和无源阻抗方案的有效性，采用RT-box 半实物仿真平台搭建双母线直流微电网模型。受系统硬件和数字处理器资源限制，设定子网1为1台储能Buck／Boost变换器和阻性负载并联，子网2 为96 V 恒压源和阻性负载并联，且工作于模式2。其中，母线电容为2200 μF，开关频率为10 kHz，下垂系数为0.08，低、高压侧母线额定电压分别为48、96 V。设定以下3种工况进行实验验证：

（1）工况1未加入无源阻抗，初始状态下子网1、2 的负载电阻值分别为20、30 Ω，闭合负载阶跃开关后，子网1、2 的负载电阻值分别为12、30 Ω，持续一段时间后断开负载阶跃开关，恢复为初始状态；

（2）工况2 加入无源阻抗（Rs3=8 Ω），其余设定与工况1相同；

（3）工况3 设定子网1、2 的负载电阻值分别为36、20 Ω，初始时刻稳定运行，一段时间后加入无源阻抗（Rs3=8 Ω）。

3种工况的实验结果见附录中图A7。由图A7（a）可知，工况1 下母线1、2 的电压分别为47.5、95.2 V，负载发生突变后母线1、2的电压分别为46.4、93.2 V；子网1、2 的储能单元输出电流分别约为4.2、2.1 A，子网1的负载电流和DAB变换器输出电流分别约为2.3、1 A，发生负载阶跃后DAB 变换器输出电流减小至0.55 A，子网1、2 的储能单元输出电流和子网1 的负载电流分别增加至5.3、2.6、3.7 A，子网1负载电流纹波系数为11.5%。由图A7（b）可知，与工况1 相比，工况2下子网1的负载电流纹波系数从11.5%下降到2.3%。由图A7（c）可知，工况3下子网1、2的储能单元输出电流分别约为3.8、1.6 A，子网1 的负载电流和DAB 变换器输出电流分别约为1.25、1.3 A，加入无源阻抗后（负载参数不变），各单元电流基本不变，且相较于工况1，子网1 的负载电流纹波系数从11.5%降低为2.3%。

从上述实验结果可知，DAB 变换器的柔性功率传输能实现各微电网内储能单元功率自动均分、母线电压恒比例控制；无源阻抗在不改变储能单元和DAB 变换器功率的情况下，能够降低负载电流的纹波系数，从而提高系统的供电稳定性。