基于椭球拟合的三轴磁强计两步校准法
2021-05-18于向前肖池阶曲亚楠宗秋刚陈鸿飞施伟红王永福宋思宇邵思霈
于向前,刘 斯,肖池阶,曲亚楠,宗秋刚,陈鸿飞,邹 鸿,施伟红,王永福,陈 傲,宋思宇,高 爽,邵思霈
(1.北京大学地球与空间科学学院,北京 100871;2.长沙理工大学物理与电子科学学院,湖南长沙 410114;3.北京大学物理学院,北京 100871;4.山东航天电子研究所,山东烟台 264003)
0 引言
在空间磁场探测中,三轴磁强计是最常用的探测设备[1-4]。彼此正交的3个磁场传感器分别测量沿正交坐标系各个轴向的磁场分量。三轴磁强计由于受自身制造工艺的影响,会存在灵敏度误差、三轴不正交性误差和零位偏差,因此在使用前必须先进行严格的标定[5]。灵敏度误差是由于三轴磁传感器各轴的灵敏度不同、测量信号的放大电路特性不完全相同而引起的测量误差;三轴不正交误差是指由于在制造过程中,3个磁传感器的测量轴无法保证两两完全正交所引起的;零位偏差是由于磁场传感器、模拟电路和 A/D 转换的零点不为0而产生的[6-8]。这些误差通常需要在地面实验室进行校准试验,得到校准矩阵用以修正在轨测量数据。目前公开报道的国内外文献主要集中在椭球拟合法。椭球拟合法需要通过迭代计算来完成参数的非线性优化求解,计算过程较为复杂,计算误差也容易积累[9-10]。本文在传统的椭球拟合的基础上,提出了两步校准法。第一步引入中间变量,采用最小二乘法求解准线性方程来获得最优解,完成对总磁场和零位偏差的校准。第二步通过求解非线性方程组,完成灵敏度误差和三轴不正交性误差的校准。
1 理论基础
当一个理想的三轴磁强计在恒定磁场中任意旋转时,磁场的3个分量应该形成一个球体。如方程(1)所示:
(1)
然而,对于一个真实的三轴磁强计,存在灵敏度误差(3个轴分别为a、b和c)、三轴不正交性误差(定义为磁强计各个轴之间的正交性偏差)和零位偏差(3个轴分别为x0、y0和z0)[11]。不正交性角度定义如图1所示。

图1 不正交性角度定义
假设o-xyz是理想传感器的正交坐标系,o-xsensysenszsens是实际传感器坐标系。假设o-xsens轴与o-x轴完全对齐,平面x-o-y与平面xsens-o-ysens共面。ρ表示轴o-y和o-ysens之间的夹角,λ表示轴o-zsens和平面y-o-z之间的夹角。φ表示轴o-z和轴o-ysens在平面y-o-z上的投影之间的夹角。
因此,用实际磁强计测量的磁场三分量使预期的球体扭曲成球心点不在原点的椭球体。如式(2)~式(4)所示[12]:
(2)
(3)
(4)
由式(2)~式(4)求解出Bx,By和Bz,可得:
(5)
(6)
(7)
将式(5)~式(7)带入式(1)中可得:
(8)
这里引入中间变量a1~a6,其中
(9)
(10)
(11)
(12)
(13)
(14)
本文提出的两步校准法,第1步采用最小二乘法求解准线性方程(8),可以得到中间变量a1~a6和3个轴的零位偏差x0、y0和z0,可以完成对总磁场和零位偏差的校准。第2步通过求解非线性方程组(9)~(14),完成灵敏度误差和三轴不正交性误差的校准。
2 数值模拟
为了验证所提出的基于椭球拟合的三轴磁强计两步校准法的有效性,本节在MATLAB环境下对该方法进行数值模拟。在模拟中,三轴磁强计将在磁场强度为50 000 nT的均匀恒定磁场中旋转,记录不同姿态下的磁场3个方向的测量数据。
预设的误差参数,包括灵敏度误差、三轴不正交性误差和零位偏差,如表1所示。

表1 预设的误差参数
利用球面上的800个随机姿态得到了三轴磁强计的3个方向上的预设测量值。为了使模拟计算更接近实际情况,这里的磁场预设测量值均取小数点一位有效数字。
然后将预设测量值带入准线性方程(8)中,采用最小二乘法求解,可得到中间变量a1~a6和零位偏差x0、y0和z0。求得的参数如表2所示。

表2 第1步求得的校准系数
利用第1步求得的参数可以完成对总磁场和零位偏差的校准。总磁场校准前后的偏差如图2和图3所示。图中实线为磁场真值。校准前的RMS误差为1 642.386 nT(3.28%)。第1步校准后的RMS误差为0.029 nT(0.6×10-6)。

图2 总磁场校准前的偏差

图3 总磁场经过第1步校准后的偏差
然后利用第1步求解出来的中间变量a1~a6通过求解式(9)~式(14),给出灵敏度误差和三轴不正交性误差校准系数。结合第一步得到的零位偏差x0、y0和z0,可得到所有的校准系数。如表3所示。与表1预设的误差参数相比,可以发现,误差主要集中在3个角度,这个误差主要是在第2步的分线性求解过程形成的。
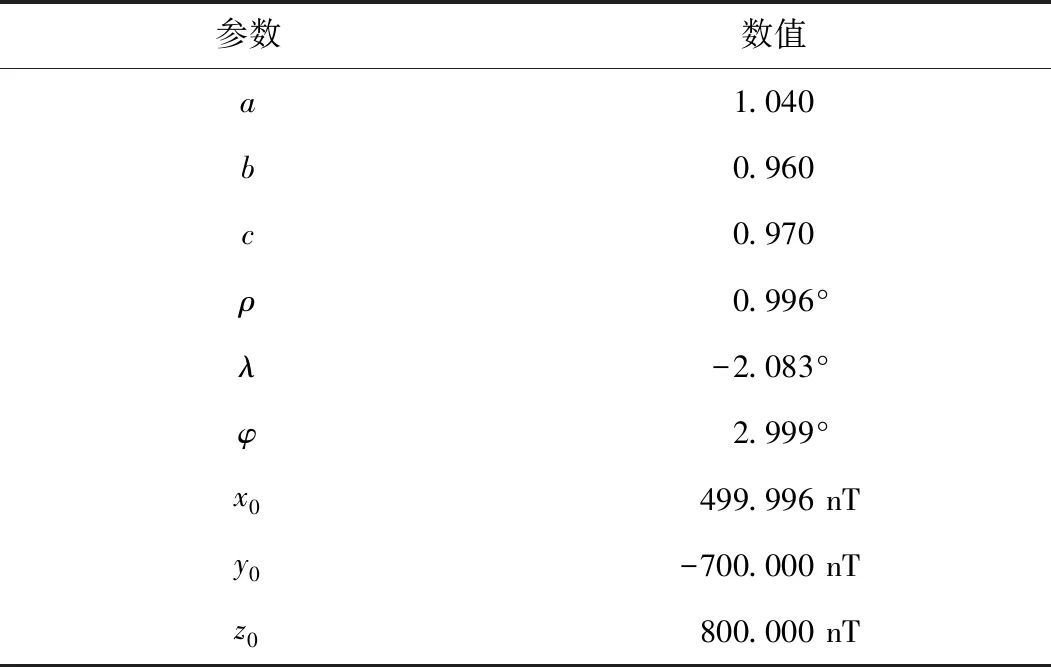
表3 第2步得到的校准系数
将表3中的系数带入式(5)~式(7),即可得到校准后的3个磁场分量。第2步校准前后的磁场的RMS误差如表4所示。
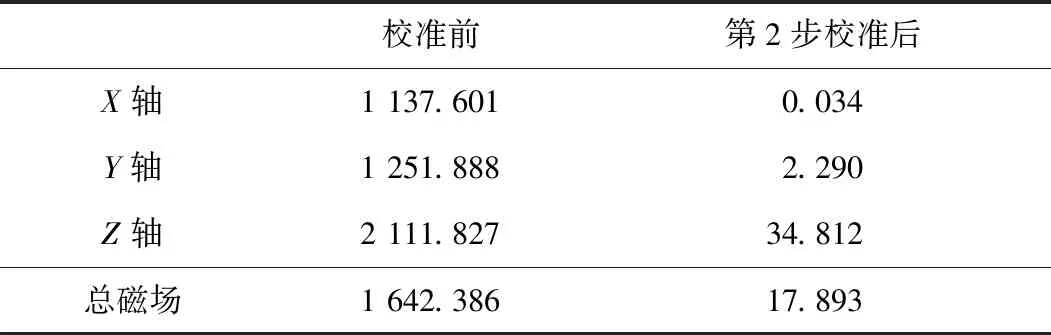
表4 第2步校准前后的磁场的RMS误差 nT
第2步校准后得到的总磁场的RMS误差为17.893nT(0.036%)。要大于第1步得到的RMS误差0.029nT(0.6×10-6)。这说明第1步引入中间变量,通过求解准线性方程寻找最优解,有效避免了计算误差的累积。
3 实验验证
为了验证该误差补偿方法的正确性和有效性,本节以北京大学研制的拟搭载风云三号气象卫星上的三轴磁强计为例进行实验验证。首先将磁场传感器固定在三维无磁转台上,然后将三维无磁转台放置在如图4所示的实验装置的中心位置,该实验装置可以排除地磁场的干扰,同时施加一个标准磁场。实验中施加幅值为50 000 nT左右的恒定磁场。然后将磁场传感器在一个球体上均匀地旋转32个方位角,并在每个方位角处将传感器停留并采集至少100 s数据。然后将3个轴的实际测量值带入式(8)中,采用最小二乘法求解,可得到中间变量a1~a6和零位偏差x0、y0和z0。求得的参数如表5所示。

图4 磁强计性能测试设备

表5 第1步求得的校准系数
利用第1步求得的参数可以完成对测量的总磁场和零位偏差x0、y0和z0的校准。校准前后总磁场的偏差如图5、图6所示。校准前的RMS误差为1 401.274 nT(2.78%)。经过第1步校准后的RMS误差为4.941 nT(0.01%)。

图5 校准前总磁场的偏差

图6 经过第1步校准后总磁场的偏差
然后利用第1步求解出来的中间变量a1~a6,通过求解非线性方程组(9)~(14),给出灵敏度误差和三轴不正交性误差校准系数。结合第一步得到的零位偏差,可得到所有的校准系数,如表6所示。

表6 校准得到的灵敏度误差和三轴不正交性误差校准系数
将表6中的系数带入式(5)~式(7),即可得到校准后的3个磁场分量和总磁场。鉴于实验条件所限,这里仅能给出经过第2步校准后的总磁场的偏差,如图7所示。经过第2步校准后的总磁场的RMS误差为6.797 nT(0.013%)。

图7 第2步校准后总磁场的偏差
第2步得到的总磁场的RMS误差要大于第1步得到的RMS误差。这说明第2步通过迭代计算来完成参数的非线性优化求解,计算误差较大。第1步引入中间变量,采用最小二乘法求解准线性方程获得最优解,完成对总磁场和零位偏差的校准,有效避免了计算误差的累积。如果只关心总磁场的校准,可以只用第1步进行校准。
4 结束语
本文在传统的基于椭球拟合的校准法的基础上,提出了两步校准法。第一步引入中间变量,采用最小二乘法求解准线性方程来获得最优解,完成对总磁场和零位偏差的校准。第二步通过求解非线性方程组,完成灵敏度误差和三轴不正交性误差的校准。该方法通过引入中间变量,有效避免了计算误差的累积。实验结果与理论分析和数值模拟相吻合。从而验证了本文所提方法的有效性。
