隧道式压气机工作轮多场耦合强度分析

黄仕豪，续彦芳，黄 若，郭文杰

(1.中北大学能源动力工程学院，山西 太原 030051)(2.北京理工大学机械与车辆学院，北京 100081)

涡轮增压器利用发动机排出的废气推动涡轮旋转，同时带动同轴的压气机向发动机气缸输送高压空气。压气机工作轮在工作过程中承受高速旋转带来的离心载荷，以及空气气动载荷、压缩空气热量产生的温差热载荷和不均匀流场相互作用产生的振动交变负荷等，受力情况极为复杂。发动机性能的不断增强使得涡轮增压器的压比和转速不断提高，压气机工作轮的机械、气动与热负荷也随之增加。与此同时，寿命要求更长、成本要求更低，使得传统的叶片式工作轮对材料性能的要求大幅度提高。新型隧道式工作轮[1]作为一种闭式旋转机械，其具有强度高、泄漏损失小、流线设计优化空间大、能适应高转速等优势。

压气机工作轮的强度分析和气动分析的结果是相关联的，气动分析所产生的流道内表面压力载荷以及热应力分析结果可以在强度分析中进一步讨论[2]。对于高速、高压比的压气机工作轮，低周疲劳是其主要失效模式[3]。压气机工作时，隧道轮受到气流场、温度场、应力场等多场耦合的综合影响，结构设计不佳与动力学特性耦合也容易造成压气机工作轮一次性强度破坏。为了确保隧道轮在试验阶段以及工作过程中能够保持安全、可靠，那么确定其极限转速、低周疲劳临界转速是十分有必要的。

本文采用全尺寸完整模型，综合考虑压气机工作过程所受的机械载荷、气动载荷与热负荷，对某新型隧道式压气机工作轮进行耦合强度分析。

1 建模与计算方法

文献[4]～[7]主要考虑离心力与气动力，采用不同的简化方法与模型，运用单向流固耦合方法对叶轮强度进行分析，其结果与试验结果相符合，验证了模型与计算方法的正确性。

本文的研究对象为某新设计的单级低压比隧道式压气机轮，其模型如图1所示，主要结构特征与参数如下：1)压气机工作轮采用流线隧道式结构，共有6组18个流道，每组流道分为长流道(第一流道)、中流道(第二流道)与短流道(第三流道)；2)扩压器采用无叶扩压器；3)隧道轮进口直径为54.8 mm，出口直径为71 mm，隧道轮出口宽度为7.2 mm；4)设计点转速为66 232 r/min，压比为1.61，质量流量为0.117 kg/s;5)最大工作转速为110 000 r/min，总压比为3.2，质量流量最大为0.182 kg/s。

图1 隧道轮三维模型

数值计算基于ANSYS Workbench搭建流-热-固耦合平台。由于最大工作转速时隧道轮内部流场最复杂，受到的离心力最大，对隧道轮的强度要求最高，因此本文对比分析隧道轮在最大工作转速下受到离心载荷、离心-气动耦合载荷、离心-热耦合载荷以及离心-热-气动耦合载荷等4种载荷作用下的应力与变形。首先，对压气机全流道进行三维定常数值模拟，得到最大工作转速下隧道轮流道表面的温度和压力分布；然后，将流体分析得到的流道壁面温度分布作为隧道轮热稳态分析的边界条件，得到隧道轮整体的温度分布；最后，将流体分析的气动载荷、热稳态分析的温度分布以及高速旋转产生的离心力作为流固耦合、热固耦合、流热固耦合时的载荷，从而得到不同载荷下隧道轮的应力以及变形的分布情况。具体计算过程如图2所示。

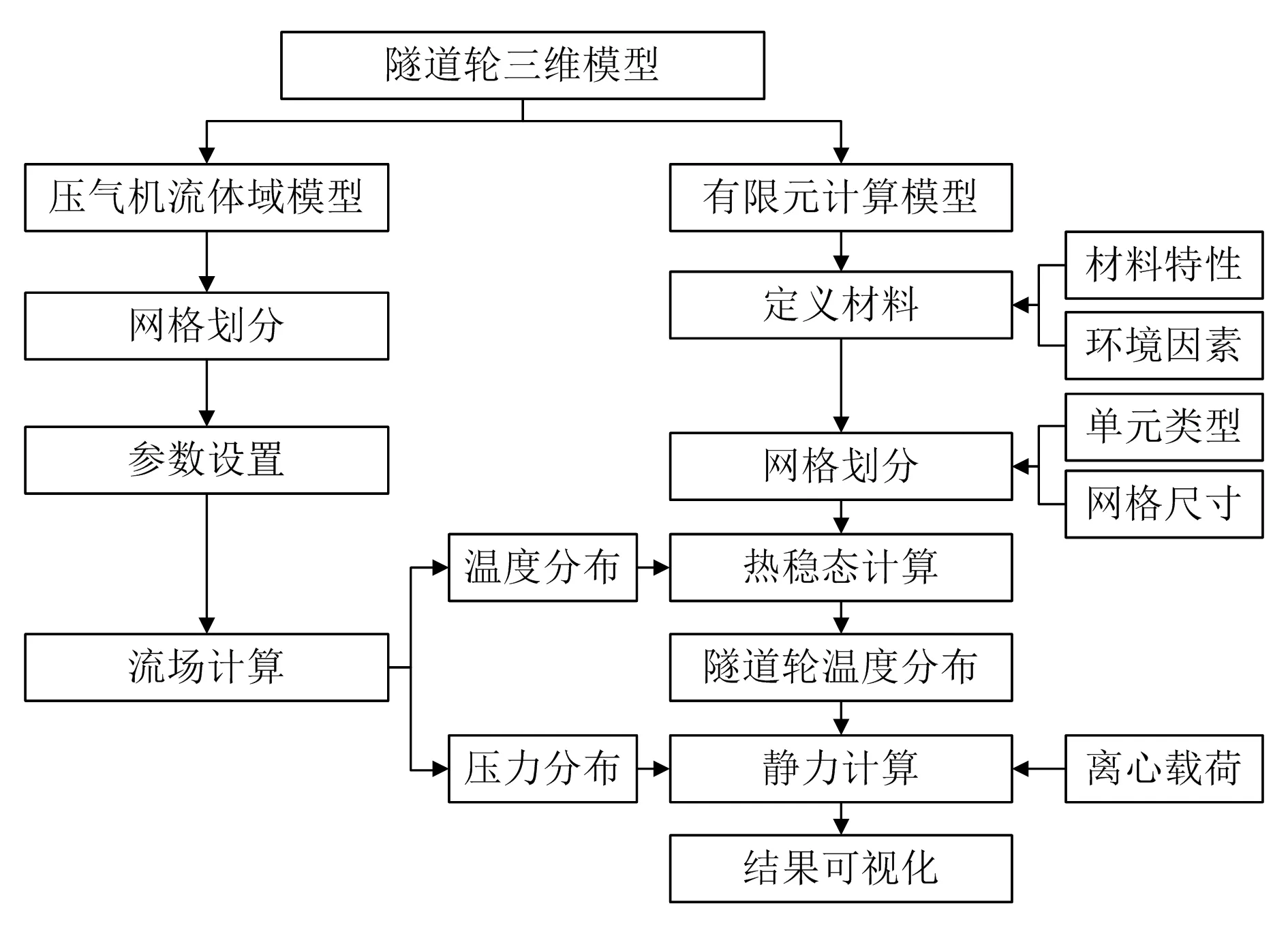
图2 计算流程

2 计算与分析

2.1 压气机流体动力学分析

2.1.1流体计算模型与计算参数设置

压气机流体域模型如图3所示。

由于流道均为管状结构，因此适合采用O形网格对入口流域、隧道轮旋转流域以及出口流域分别划分网格。交界面设置为interface面，用于进行节点数据的传递。经过网格无关性验证后，当各部分网格数量达到表1所示的数量时，满足计算要求，压气机压比和效率随网格数量的变化如图4、图5所示。

图3 压气机流体域模型

表1 流体域网格分布

图4 压比随网格数量变化曲线图

图5 效率随网格数量变化曲线图

在最大工作转速下用Fluent软件对压气机全流场进行计算。工质为理想空气，转速为110 000 r/min，边界条件主要包括进口、出口和固壁。对于进口条件，压气机入口为大气，因此以大气总温和总压作为边界条件，分别为298.15 K和101 325 Pa，气流方向为轴向，即垂直于入口截面；对于出口条件，一般采用给定流量方法，出口处质量流量设置为0.182 kg/s；对于固壁条件，不考虑换热的影响，对转子给定相应转速，其余壁面转速设置为0。另外，采用转子冻结法处理转静交界面，使转、静子内的流动分别在相对、绝对坐标系下求解，最终解取决于转、静子的相对位置。这种方法最适合周向流动变化不能忽略的转静子面，例如隧道轮和扩压器的交界面。求解器设置为稳态Pressure-Based，速度方程采用绝对速度；湍流模型为Spalart-Allmaras模型。采用Fluent中Hybrid初始化方法，迭代50步，压力-速度耦合算法选择SIMPLEC，计算2 500步。

2.1.2流场计算结果

流体动力学分析的结果可作为后续热稳态分析和结构静力学分析的边界条件。隧道轮流域壁面的静压分布和温度分布如图6所示。

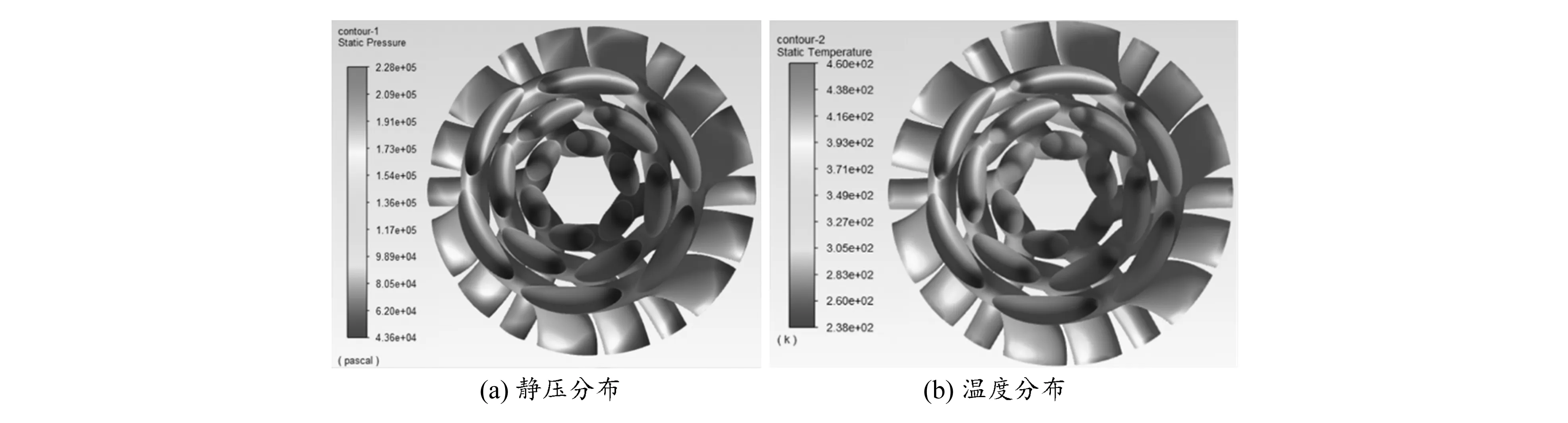
图6 旋转流域壁面静压和温度分布

气体从流道入口进入，随着隧道轮对气体做功，其温度和压力沿着流道逐渐增大，在流道出口处达到最大值，最高温度为460 K，最大静压为0.228 MPa。传递到隧道轮流道表面后的结果如图7所示。

流道表面的压力和温度分布与流固耦合面保持一致，但是由于流体分析和有限元分析采用的不是同一个网格模型，导致压力和温度值有所变化，此时的最高温度为445.58 K，最大压力为0.233 MPa。

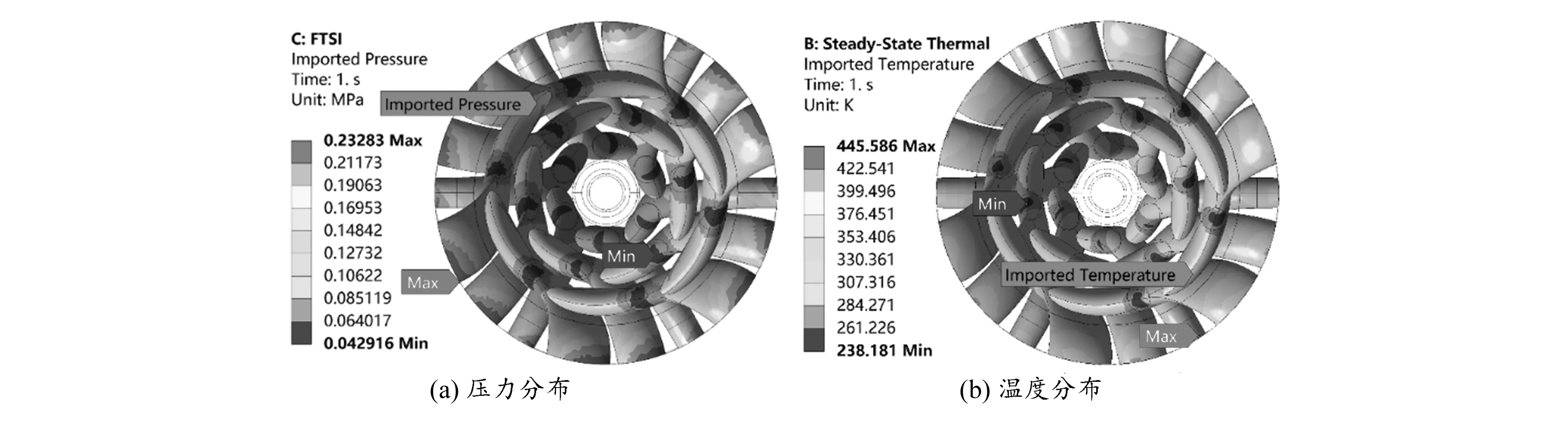
图7 隧道轮流道表面压力和温度分布

2.2 隧道轮热稳态计算

隧道轮所采用的材料为TC11，具体参数见表2。

表2 隧道轮材料性能

在压气机工作一段时间之后，受到流体温度的影响，隧道轮的整体温度分布不再随时间变化，从瞬态热问题变为稳态热问题，各向同性材料的热稳态导热微分方程为：

(1)

式中：λ为导热系数；T为温度；x,y,z为坐标轴的3个方向；s为单位微元体内热源产热。

2.2.1有限元模型网格划分

在ANSYS Workbench搭建的耦合平台中，热稳态分析模块和结构静力学计算模块可以共用网格。由于隧道轮结构较为复杂，因此在划分网格时采用适应性较强的四面体单元，初步划分网格后计算单独考虑离心力时的最大应力，并在得到计算结果之后对应力集中的区域进行更为精细的网格划分，使得应力结果覆盖两层单元。为了确保计算结果的准确与可靠，同时达到最高的计算效率，需要对初步划分的网格模型进行网格无关性检验。从图8中可以看出,当网格单元的数量超过80万后，应力的大小不再随单元数量的变化而变化。因此，最终确定的网格节点数为1 342 747，单元总数为866 538，网格平均质量为0.782。利用上述建立好的网格模型，将2.1.2中得到的隧道轮流道表面温度分布作为热稳态分析模块的初始条件进行隧道轮热稳态计算。

图8 最大应力随网格数变化曲线

2.2.2热稳态计算结果

根据上述网格模型和边界条件计算得到的隧道轮整体温度分布结果如图9所示。该结果可作为结构静力学分析的热边界条件。

2.3 隧道轮最大工作转速下的强度分析

基于在ANSYS Workbench中搭建的流-热-固耦合平台，利用2.2中建立的隧道轮有限元网格模型，采用单向流-固耦合、单向热-固耦合、单向流-热-固耦合方法在最大工作转速下对离心载荷、离心-气动耦合载荷、离心-热耦合载荷、离心-热-气动耦合载荷这4种载荷状态下的隧道轮的强度进行计算分析。其中：1)气动载荷为2.1.2中得到的隧道轮流道表面压力分布；2)热载荷为隧道轮内部温度差异造成的热应力，其热边界条件为2.2.2中得到的隧道轮温度分布；3)离心载荷为隧道轮绕z轴转速度110 000 r/min时产生的离心力Pi：

图9 隧道轮整体温度分布

(2)

式中：mi为单元质量；ω为转速；Ri为单元半径；ρ为材料密度；Vi为单元体积；N为转速。

约束条件：考虑到隧道轮的实际装配情况，对隧道轮轮毂前后端面以及轴孔面施加固定约束。

本文采用Von Mises准则对叶轮强度进行判断分析。图10～图13分别为不同载荷状态下的应力以及变形情况。

图10 离心载荷作用下的隧道轮应力及总变形

4种载荷情况下隧道轮中的最大应力、最大变形以及相对于仅考虑离心载荷时的变化率数据见表3。

由图10～13及表3中的数据可以看出：

1)4种不同载荷下，隧道轮的最大应力点均位于第一流道中部靠近第二流道的区域，其原因主要是，在隧道轮内部，流道的截面形状为圆形或者椭圆形，流道与流道之间的壁厚分布不均匀，导致在高速旋转过程中，隧道轮壁厚最薄的地方会产生较大的应力。

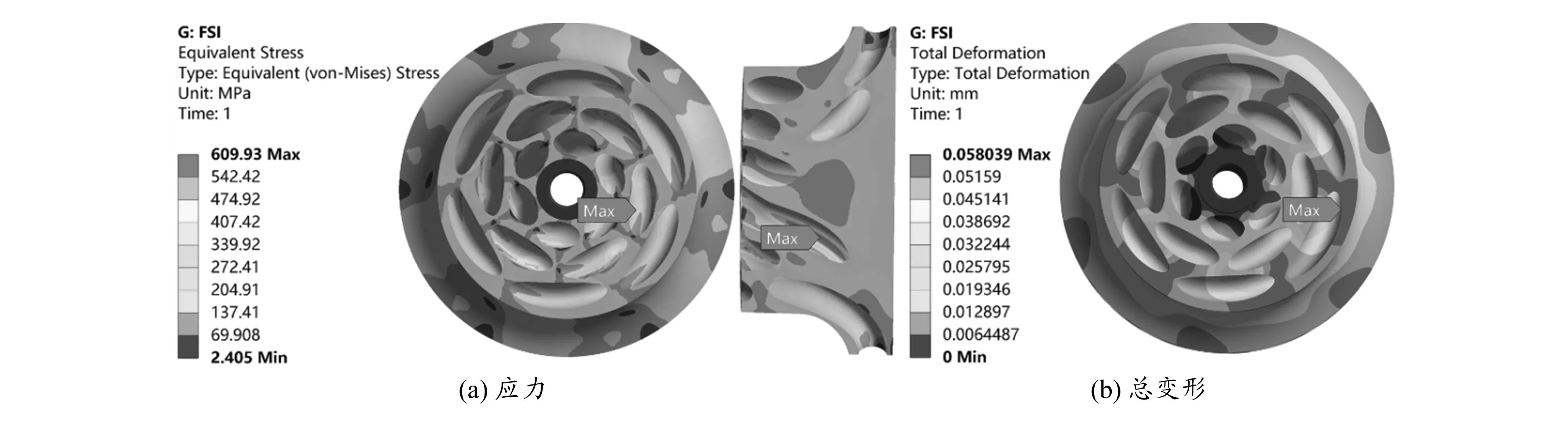
图11 离心-气动耦合载荷下的隧道轮应力及总变形

图12 离心-热耦合载荷下的隧道轮应力及总变形

图13 离心-热-气动耦合载荷下的隧道轮应力及总变形

表3 不同载荷下隧道轮最大应力、变形及变化率

2)在仅考虑离心载荷时，隧道轮的最大变形位置位于第三流道入口处靠近隧道轮边缘以及第三流道出口轮盖处的区域，其原因主要是这两个区域的壁厚较薄、旋转半径大，高速旋转时受到较大的离心力，使得该区域的变形最大；加上气动载荷后，最大变形量有所增加，但是最大变形位置没有发生改变；加上热载荷后，最大变形量增加较为明显，且最大变形位置变为第三流道出口轮盖处，造成这种变化的原因是该位置热应力比入口位置大，加上离心力之后使得最大变形位置以及最大变形量发生了改变。

3)通过对不同载荷下隧道轮应力应变情况的定量对比分析可知，气动载荷对于隧道轮的应力影响较小，在考虑气动载荷与离心载荷的情况下，隧道轮最大应力相比于仅考虑离心载荷时增加了0.12%，最大变形增加了0.33%；热载荷对隧道轮的应力影响也不是很大，在考虑热载荷与离心载荷的情况下，隧道轮最大应力相比于仅考虑离心载荷时增加了6.31%，最大变形增加了29.34%；而在综合考虑气动载荷、热载荷与离心载荷时，隧道轮最大应力相比于仅考虑离心载荷时增加了6.42%，最大变形增加了29.61%。对于小流量低压比的隧道轮，离心载荷是主要的应力来源，气动载荷及热载荷对隧道轮的应力影响较小，但是也不能忽略，尤其是在计算隧道轮的极限强度和低周疲劳临界转速时。

4)在最大工作转速时，综合考虑离心载荷、热载荷与气动载荷，计算得到的最大应力值为648.32 MPa，隧道轮材料为TC11，其屈服极限为910 MPa，在设计转速时取安全系数为1.4，许用应力为650 MPa，隧道轮最大应力在许用应力范围内，满足强度要求。

2.4 隧道轮极限转速、低周疲劳临界转速的确定

针对本文所设计的隧道轮综合考虑离心载荷、气动载荷与热载荷，在ANSYS Workbench中进行了有限元计算，得到了屈服强度以及抗拉强度所对应的转速。屈服强度对应的应力计算结果如图14 所示，抗拉强度对应的应力计算结果如图15所示。当隧道轮的转速达到135 000 r/min时，最大应力值达到917.58 MPa(TC11的屈服强度为910 MPa)，按照低周疲劳的概念，服役的构件中，在某一部分材料(局部)所受应力超过材料的屈服强度时，即进入低周疲劳状态。对于本文所设计的隧道轮，最大应力值已经超过了材料的屈服强度，该转速即为所设计的隧道轮的低周疲劳临界转速。隧道轮的转速达到143 500 r/min时，最大应力值为1 036.8 MPa(TC11的抗拉强度为1 030 MPa)，理论上讲，这种情况下最大应力位置处会产生一次性强度破坏，出现裂纹。对于本文所设计的隧道轮，最大应力值已超过材料的抗拉强度，此转速即为所设计隧道轮的极限转速。

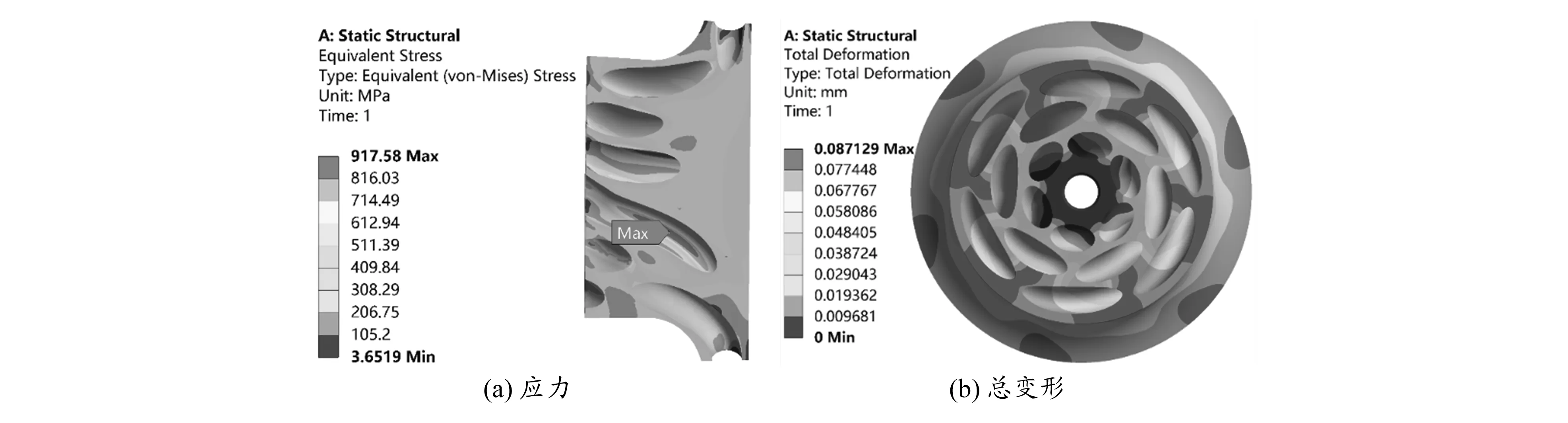
图14 135 000 r/min的应力及变形分布

图15 143 500 r/min的应力及变形分布

3 结论

本文通过建立流-热-固耦合平台，分析了最大工作转速下不同载荷对隧道轮应力及变形的影响，综合考虑离心、气动与热载荷，计算得到隧道轮的低周疲劳临界转速以及极限转速得到如下结论：

1) 对隧道轮应力大小和分布情况影响程度的大小依次是离心载荷、热载荷与气动载荷。

2) 最大工作转速时，综合考虑离心载荷、气动载荷以及热载荷所计算得到的隧道轮最大应力为648.32 MPa，在材料的许用应力范围内，满足强度的要求。

3)最大工作转速时，综合考虑离心载荷、气动载荷以及热载荷所得到的隧道轮的最大变形为0.075 mm，可为压气机设计时确定各个部件之间间隙提供参考。

4)综合考虑离心载荷、气动载荷以及热载荷时，计算得到的隧道轮低周疲劳临界转速为135 000 r/min，极限转速为143 500 r/min，可以作为压气机疲劳试验时最高转速的参考转速。