严重事故熔池关键现象的MPS模型优化

朱影子,熊进标

(上海交通大学 核科学与工程学院,上海200240)

核反应堆发生失水事故后,堆内冷却剂大量丧失,导致燃料元件冷却不足,发生堆芯熔化事故[1-3]。当堆芯熔化过程发展到一定程度,堆芯熔融物将落入压力容器的下腔室,在瞬态熔池形成过程中,未熔化的堆芯材料,包括:锆合金包壳,不锈钢结构件,铟科镍定位格架等在燃料衰变热的加热下继续熔化。熔化后的材料间存在密度差,则会发生密度分层现象,进而影响压力容器下封头热流密度的分布,对其结构完整性造成威胁。因此,有必要探索熔池内的固体块熔化分层的机理,为核反应堆安全分析提供相应的理论支持。

关于固体的熔化现象,已经有很多的研究,其中Guo等[4]运用有限体积粒子法模拟了伍德合金的熔化,并与实验作对比,模拟结果与实验吻合较好。Li 等[5]对两种密度不同、粘性不同的不相容液体的分层做了实验和模拟,二者结果较为吻合。在熔化分层现象的模拟中,固液相界面发生较大的变化,因此选用Koshizuka[6]提出的基于拉格朗日描述的移动粒子半隐式法(MPS),此方法没有网格约束,在计算域使用自由移动的粒子,便于处理大变形流动问题。此方法在核反应堆中[7]已应用于传热相变[8,9],液滴冲击[10],熔融物迁移[11]和熔融物-混凝土相互作用[12]等问题的模拟。

熔化分层现象涉及熔化、分层等多个物理过程,在熔化过程中使用基于焓值相变模型来模拟,并且用黏性模型来计算固、液之间的黏性变化,其中改进黏性显式算法为隐式算法来保证计算的高效性和稳定性,运用PMS模型来实现固液耦合,并将熔化模拟结果和Guo[4]的实验作对比,二者结果吻合较好。同时对两种不同密度、不同黏性的流体做了分层模拟,模拟结果与Li[5]的实验对比,结果显示较好的一致性。最终将熔化现象和分层现象结合起来,模拟了伍德合金固体在密度较大的液体中熔化并分层的现象,并预测其熔化分层过程。

1 MPS方法

熔化过程中的控制方程包括连续性方程、动量方程和能量方程:

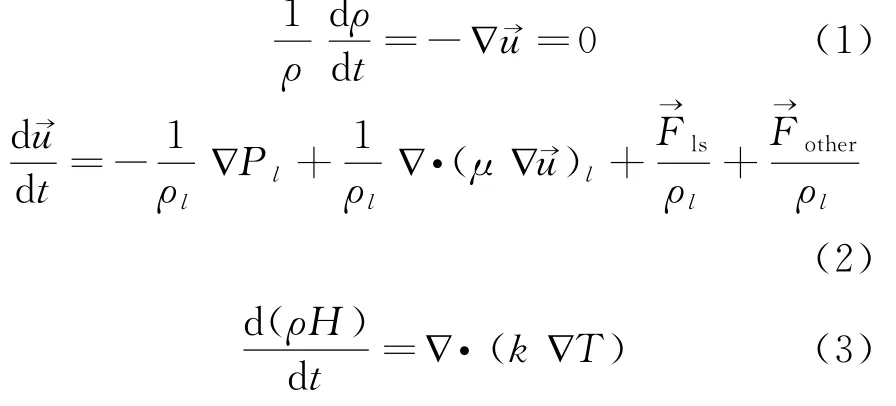
式中:ρ、ν、k——密度、运动黏度、导热系数。

方程(2)中右侧第三项为固体粒子和液体粒子之间的相互作用力,可以通过压力差近似得到:

固体的控制方程为:

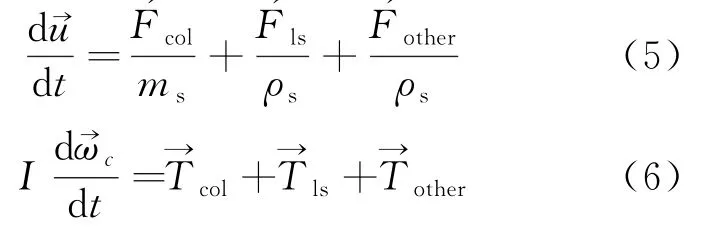
在粒子法中,控制方程的离散是通过粒子间相互作用模型实现的,如图1所示。其中核函数是最基本的模型,如公式(7)所示,是用来计算粒子数密度的一个权重函数,有很多类型,这里采用Koshizuka[6]提出的模型,如图2。

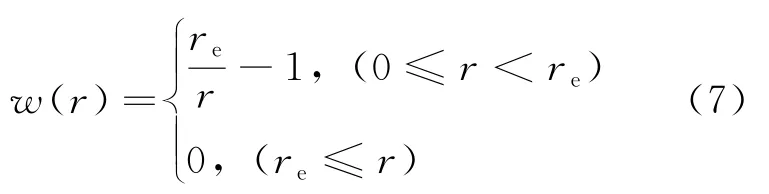
式中:re——有效半径,只有作用域内的粒子之间有相互作用,此值一般取粒子直径的2～3倍。

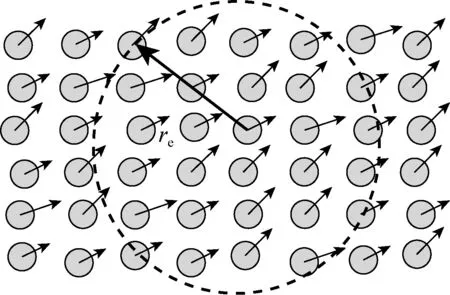
图1 粒子有效半径Fig.1 The cut-off radius

图2 核函数Fig.2 Kernel function

梯度算子基于粒子间梯度权重平均由梯度模型离散,如公式(8)及图3所示。

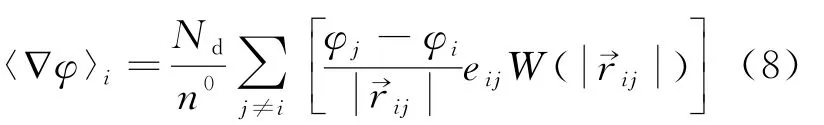
式中:N d——空间维数;

n0——初始标准粒子数密度。

为了计算的稳定性,压力计算采用了Kondo[13]改进后的梯度模型,如公式(9)所示。

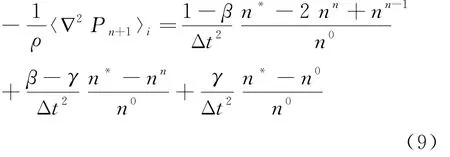
式中:β、γ——与时间步长、粒子大小等有关的修正系数。

β和γ应满足公式(10)的边界条件范围

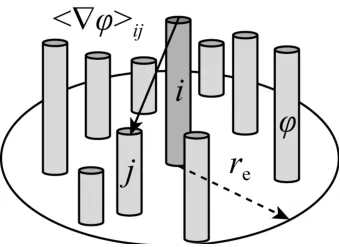
图3 梯度模型Fig.3 The gradient model

拉普拉斯模型的物理示意如图4所示。

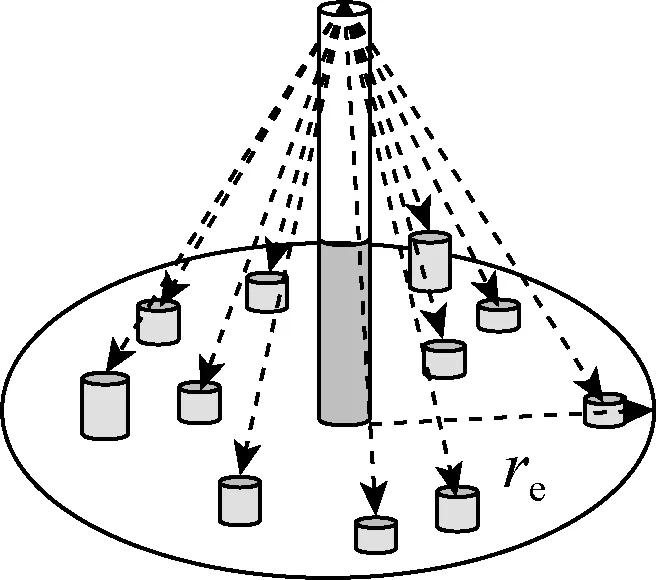
图4 拉普拉斯模型Fig.4 The Laplacian model

其中λ为修正计算结果,如公式(11)所示。

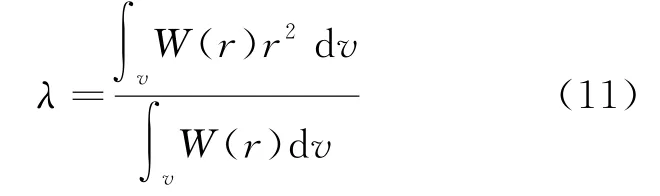
2 熔化模型

熔化是一个涉及相变的复杂物理过程,本文使用基于焓值的熔化模型来计算固-液相变过程,为了计算稳定,使用黏性模型计算固、液相变之间的黏性,应用PMS模型实现固液之间的耦合。

2.1 基于焓的熔化相变模型

固体熔化过程中的相变是由公式(3)计算,温度T和液相份额ε与焓值H的关系如公式(12)～公式(13)及图5所示。

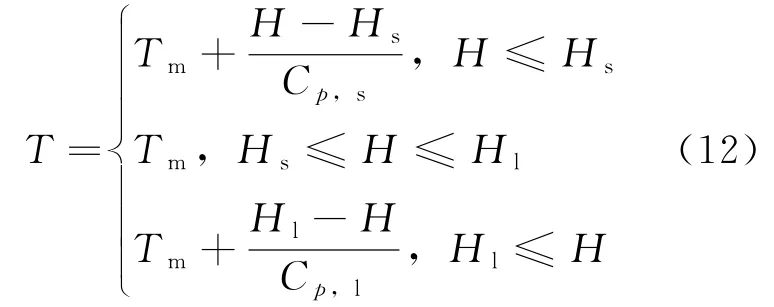
式中:C p,s和C p,l——熔化前后固相和液相的比热。

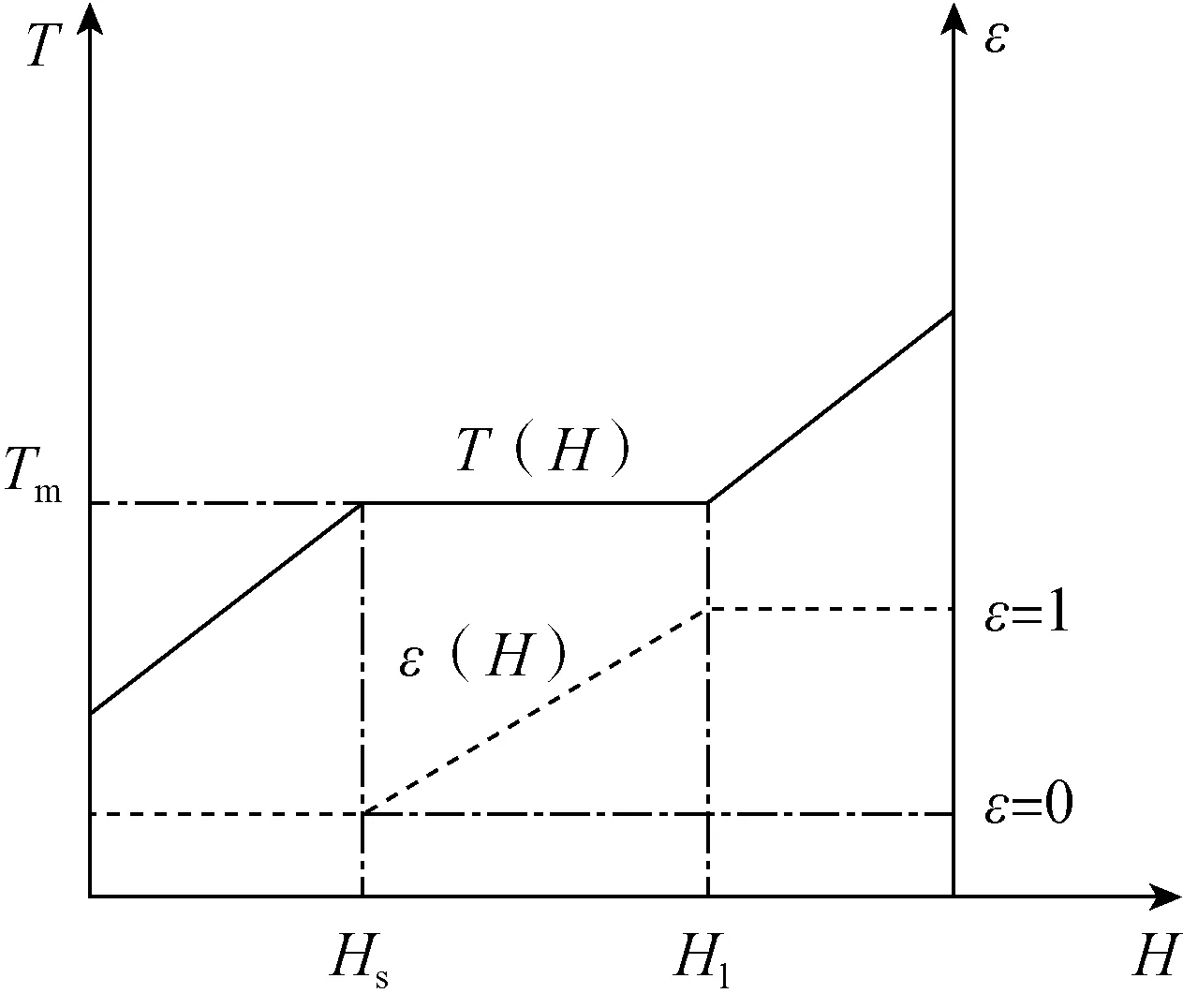
图5 基于焓值的相变模型Fig.5 The phase change model based on enthalpy

2.2 黏性模型

在实际熔化过程,固体的黏性为无穷大,远远大于液体,为了计算的稳定性,引入Ramacciotti[14]的黏性模型。

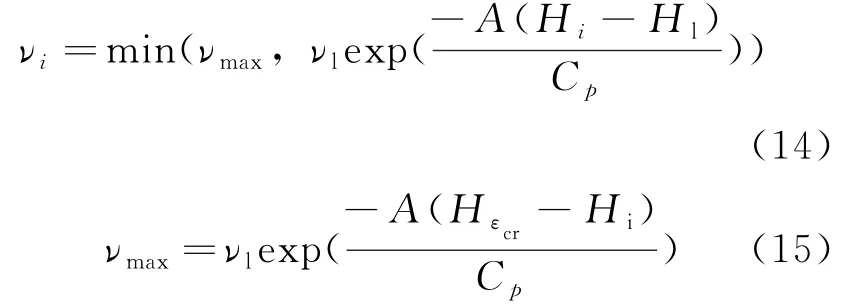
式中:νi——运动黏性;

Hεcr——固体粒子变为液体粒子的临界焓值,一般取εcr为0.375时的焓值;

A——流变 系 数,根 据Guo[4]的 研究,A取值为0.054。

固体的黏性较大,要满足扩散稳定性,计算时间步长非常小,为了提高计算效率,将黏性项的显式计算改为隐式计算:

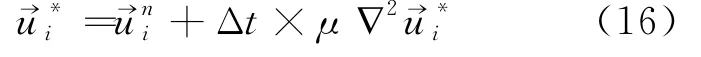
2.3 流固耦合模型

熔化过程中涉及固体向液体的转变,因此要处理流固耦合的问题,使用PMS模型[15]可以模拟此现象。其计算理论是:先将所有粒子视为液体粒子通过公式(1)～公式(3)计算其速度和位置,解能量方程由焓值判定识别固体粒子,计算固体块的速度和重心位置,最后再对固体粒子的速度和位置做修正(见公式(17)～公式(22))。

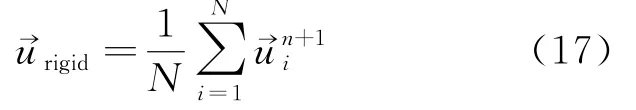
其中N是粒子总数。

粒子的几何重心为:

粒子的角速度:

每个固体粒子具有相同的密度,转动惯量I为:

最后,修正固体粒子的速度和位置:

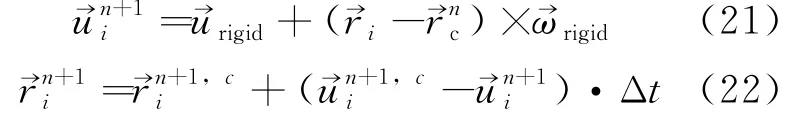
最终,计算的流程图如图6所示。

图6 计算流程图Fig.6 The workflow of the calculation

3 结果

3.1 熔化模拟

为了验证基于焓值的熔化模型的准确性,模拟了伍德合金的熔化,并与Guo[4]的实验作对比,将伍德合金置于恒定温度的加热板上,并监测熔化过程中固体块的高度和液膜扩展长度的变化。伍德合金的物理性质如表1所示,计算中忽略固、液之间密度的变化。

表1 伍德合金物性Table 1 Properties of the Wood alloy

续表

初始几何设置如图7所示,开始所有粒子均为固体粒子,初始温度均匀分布,为27℃,进行了底部加热板的温度分别为250℃,300℃和350℃的模拟。其他物理量设置均与实验相同。熔化过程持续2 s,以导热为主,此熔化过程持续时间较短,计算中忽略与空气的对流换热和辐射换热。模拟结果如图8和图9所示,与实验值相比固体块的高度变化和液膜的扩展均偏低,除了计算本身的误差以外,主要为计算中忽略辐射和对流换热。

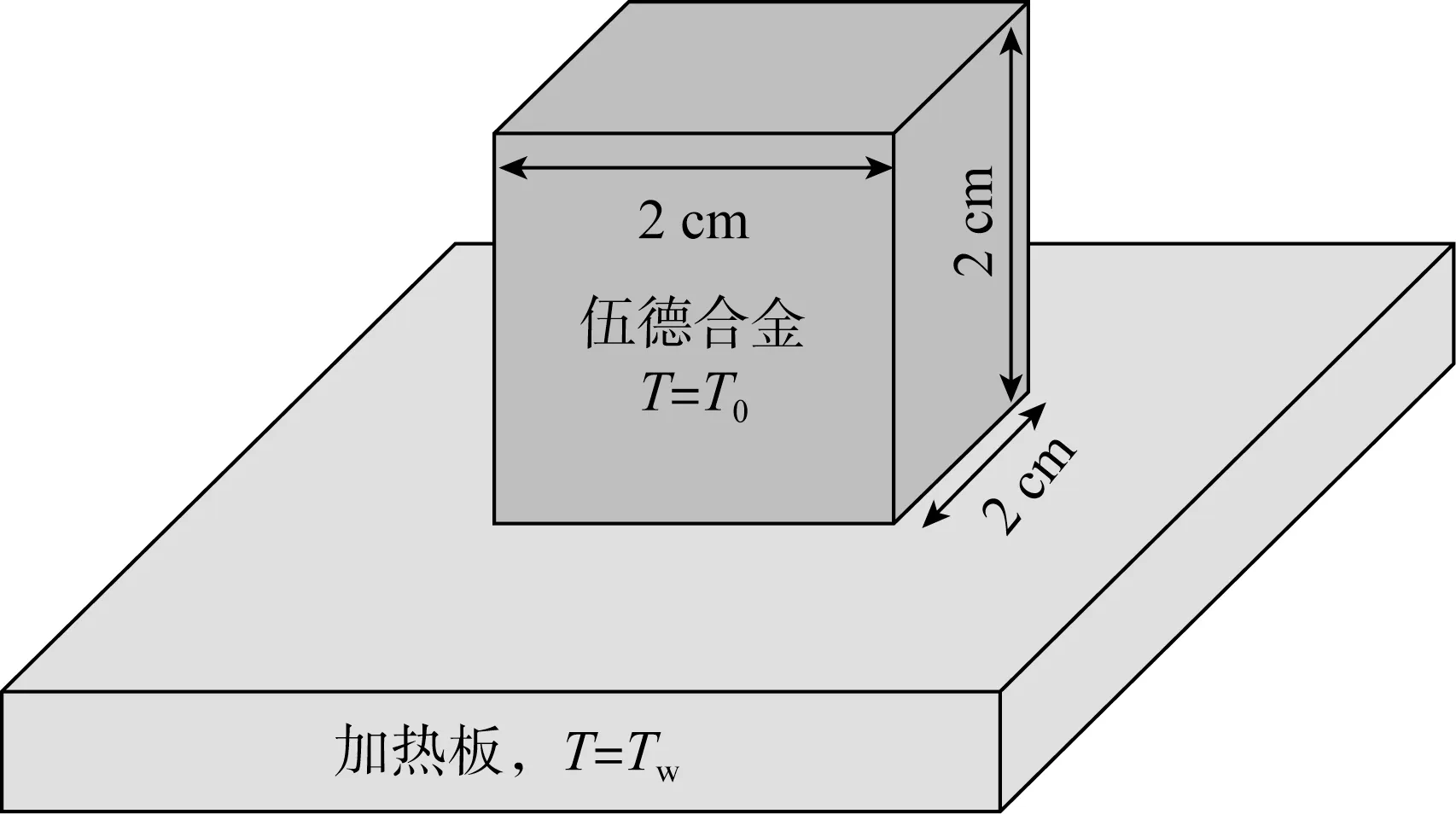
图7 熔化模拟几何Fig.7 Geometry of the Wood alloy

图8 液膜扩展长度的变化Fig.8 Variation of the spreading width

图9 固体高度的变化Fig.9 Variation of cube height

3.2 分层模拟

由于密度差产生分层是熔池形成行为中重要现象。Li[5]针对两种互不相溶的液体做了分层实验。实验描述如图10所示,初始时刻,中间有一块隔板将两种液体隔开,实验开始后,隔板以0.2 m/s 的速度向上运动。盐水的密度和黏性由其浓度决定,两种液体界面处的密度和黏性由二者的算数平均值获得。

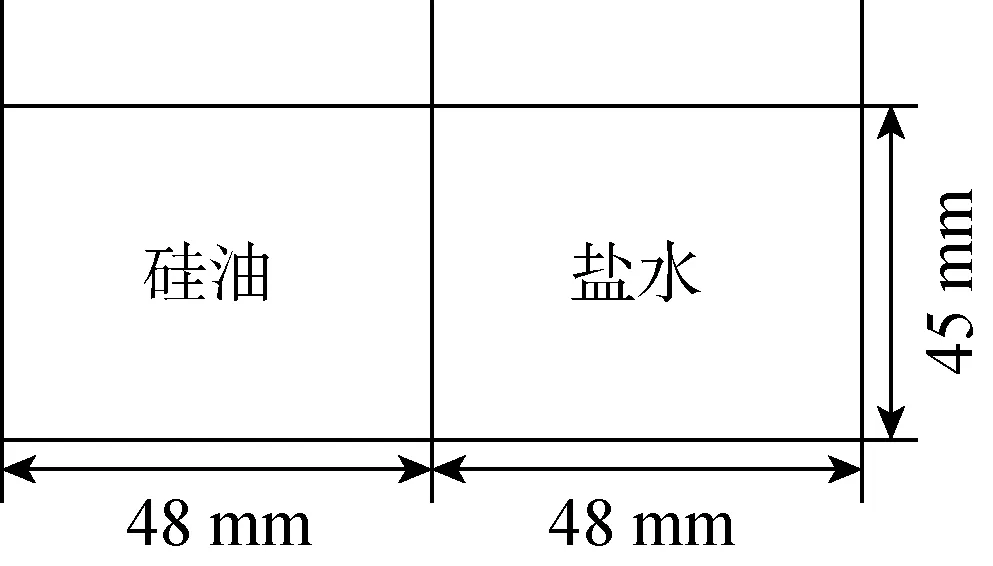
图10 分层模拟几何Fig.10 Geometry for stratification

实验分为两组,A组使用黏性较大的硅油(5000 mm2/s)和10%(质量分数)的NaCl水溶液,B组使用黏性较小的硅油(200 mm2/s)和20%(质量分数)的NaCl水溶液。实验中为了区分二者,在NaCl水溶液中添加了亚甲蓝染色剂,具体参数如表2所示。

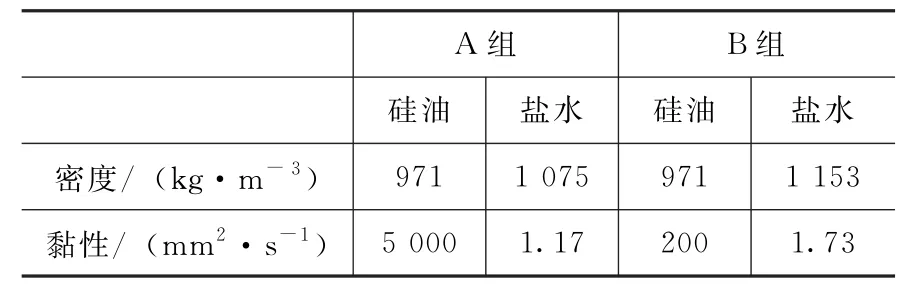
表2 两种分层液体的参数Table 2 Properties of the fluids in stratification

图11 分层实验与模拟结果对比Fig.11 Comparison of the simulation and experiment

模拟结果如图11(a)显示了黏性比较大的硅油和盐水的分层实验与模拟的对比结果,图中密度较小的硅油上浮,密度较大的盐水下沉,并最终产生稳定分层的结果。在前5 s,液体流动较快,且在容器底部出现一层硅油层,之后液体流动较为缓慢,分层形状基本不变。这是因为隔板初始抽出之后,两种液体界面有较大的压力差驱动产生较大的动能,此能量随着时间而衰减。图11(b)显示了黏性比较小的两种液体的分层结果,与A组相比,B组实验中硅油的黏性较小,盐水的密度较大,当隔板抽出后,两种液体的界面处产生瞬时震荡现象,模拟中也将这种趋势预测出。

3.3 熔化分层模拟

将熔化现象和分层现象结合起来,模拟伍德合金固体在密度较大的液体(称为背景液体)中熔化并分层的现象。其中伍德合金固体密度为8 528 kg/m3,并且固体熔化前后密度保持不变,背景液体密度为9 528 kg/m3。初始几何如图12所示,设计固体在背景液体中的位置处于其所受浮力和其重力刚好抵消,固体和液体的相对速度较小,计算中简化固体在液体中的熔化现象,忽略固、液之间的对流换热,以导热为主。假设伍德合金熔化后的液体和背景液体有相同的比热、导热系数、粘性等物理参数。初始条件:背景液体温度为350℃,固体温度为27℃;边界条件:几何左右两侧为绝热边界,底部为定温350℃。伍德合金固体熔化后的液体和背景液体的界面处,密度为二者的平均值。

图12 熔化分层模拟初始几何Fig.12 Geometry for melting and stratification

伍德合金在背景溶液中熔化分层结果的预测如图13所示,固体在63.876 s完全熔化,并稳定分层。在0～60 s中,使用不同相态区分粒子,观察固体形状的变化,浅蓝色为固体粒子,深蓝色为液体粒子,固体被加热,并逐渐熔化。65 s时,固体完全熔化并稳定分层,使用不同物质区分粒子,其中上层红色为密度较小的伍德合金熔化液体,下层蓝色为密度较大的背景液体。最终液体的压力分布符合静压分布规律,如图14所示。图15为最终的温度分布,固体熔化后的液体处温度最低,以熔化后的液体为中心,周围温度逐渐升高,底部边界维持350℃的恒温。模拟结果符合熔化分层的物理规律。

图13 熔化分层模拟结果Fig.13 Process of melting and stratification

图14 在65 s时的压力分布Fig.14 Pressure distribution at 65 s

图15 在65 s时的温度分布Fig.15 Temperature distribution at 65 s

4 结论

为了探索核反应堆严重事故后,在瞬态熔池形成过程中,燃料元件等在熔池中的熔化及分层现象。将原始的移动粒子半隐式法(MPS)进行改进,首先将压力源项改为混合源项提高压力计算的稳定性,并将黏性显式计算改为隐式算法,提高计算的效率。然后加入能量方程并对熔化过程进行建模,结合基于焓值的熔化/凝固相变模型、黏性模型、流固耦合模型等模拟了三维伍德合金的熔化现象,模拟结果与实验结果较为吻合。通过模拟互不相溶的硅油和盐水验证算法对分层现象的有效性,并与实验结果进行对比,显示较好的吻合度。最终将熔化和分层现象结合,模拟了伍德合金在背景液体中的熔化分层现象,并预测其过程,通过对结果的分析,表明该模拟符合熔化分层的物理规律。