基于运动恢复结构的无规则植物叶片面积三维测量方法
2021-05-18王婷婷代作晓黄云峰
陈 辉 王婷婷 代作晓 黄云峰
(1.上海电力大学自动化工程学院, 上海 200090; 2.中国科学院上海技术物理研究所, 上海 200083)
0 引言
叶片是植物进行光合作用、制造氧气、合成营养物质的主要器官,是进行蒸腾作用进而为根提供从外界吸收和运输水分动力的主要途径[1-2],在植物生长过程中不可或缺。叶片面积影响光截获[3]、表面蒸发以及生长量等,是研究植物生长最常用的指标之一,快速、准确、无损伤的植物叶片面积三维测量对指导现代农业生产具有重要意义。传统的植物叶片面积测量方法一般基于单个叶片进行接触式面积测量,如方格作图法、称纸重法、打孔称重法、回归方程法和数字图像处理法等[4-5],这些方法易对叶片表面造成损伤,影响三维测量结果。文献[6]提出一种基于Android手机的植物叶片面积快速无损测量系统,该系统可测量多种不同形状的植物叶片面积,由于生长形态和变形等因素使叶片不可能是一个绝对的平面,直接采用二维图像进行测量,其叶片卷曲部分将会导致测量误差。文献[7]利用不同方位光源照射下的图像明暗特征来拟合叶片空间平面,恢复叶片空间倾斜信息,虽然该方法利用了叶片在三维空间中的形态特征,但仅对于叶片无遮挡条件下的测量精度较高。文献[8]利用超体素分割和KD-tree纹理映射的贪婪投影三角化算法结合三维激光扫描点云对树木枝叶进行分割和三维重建,但三维激光扫描点云数量巨大,数据处理复杂,且所需成本高。文献[9]应用结构光视觉测量技术,利用体素滤波实现降采样,并进行平滑处理,对分割后的不同类别点云进行线性拟合,实现了棉花幼苗叶片性状解析,但基于结构光的深度图像系统对光照环境的配置要求较高。
植物叶片面积测量的难点主要是:在不接触叶片时恢复叶片的三维结构,从繁杂的背景中提取叶片结构,以及从重叠叶片中分离出单个叶片。基于上述问题,本文提出一种基于智能手机的非接触式植物叶片面积三维测量方法,从多个角度对自然生长条件下的多类别植株进行拍照,通过运动恢复结构(Structure from motion, SfM)进行三维重建,利用特征点匹配算法得到植株叶片的三维点云模型,采用颜色特征空间阈值分割对三维点云去噪,利用模糊C均值(Fuzzy C-means, FCM)聚类算法分割重叠叶片中的单个叶片,以期实现叶片面积三维测量。
1 材料与方法
1.1 植株样本材料
实验样本植株信息如表1所示,主要以四季青幼苗植株作为实验对象,分别从叶片数量及重叠率两方面分析方法可靠性,另外选择杨树、银杏树、梧桐树3类叶片完全不同的植物进行采样,从叶片形状复杂性的角度来进一步验证本文方法的有效性。
1.2 总体框架
本文方法总体结构如图1所示,主要分为图像采集、三维点云模型重建、叶片面积计算3部分。
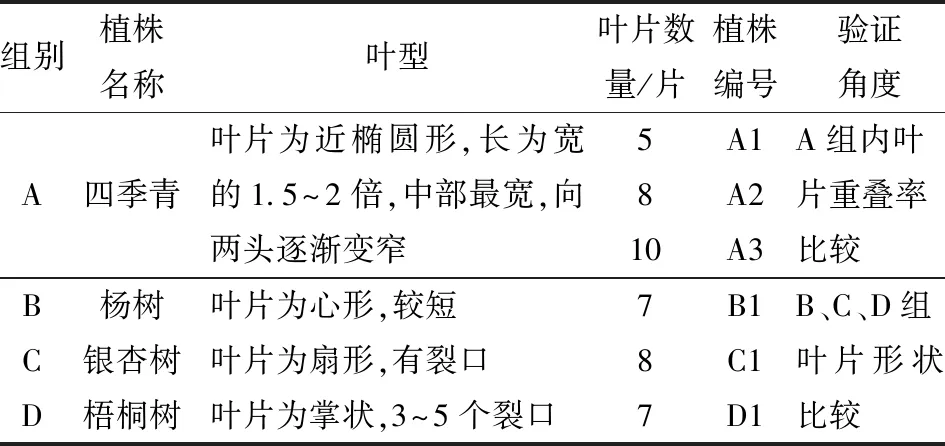
表1 实验样本植株信息Tab.1 Plant information of experiment materials
1.2.1图像采集
使用智能手机相机作为采集设备,为保证平台采集的稳定性和可行性,整个采集过程中手机相机设置为自动对焦模式,禁止闪光灯及获取HDR图像。在距离植株0.5 m范围内采集植株图像,确保相机中心共线以完成全景拼接。以植株为中心,旋转一周,每隔10°~20°拍摄一幅图像。采集的图像尺寸均为4 032像素×3 024像素,保存为JPG格式。
图2为实验采集的植株样本,A组为四季青幼苗样本,其中,A1号植株采集55幅图像,A2号植株采集86幅图像,A3号植株采集100幅图像;B1号植株为杨树苗植株样本,采集74幅图像;C1号植株为银杏树苗植株样本,采集78幅图像;D1号植株为梧桐树苗植株样本,采集79幅图像。
1.2.2三维点云模型重建
基于1.2.1节中采集的图像集,利用SfM方法进行三维重建。通过尺度不变特征转换算法(SIFT)在已建立的图像尺度空间中寻找极值点,检测其潜在的特征点[10-11],并选择最稳健点作为最终特征点。计算特征点之间欧氏距离可决定匹配度,欧氏距离越短,匹配度越高。然而,SIFT匹配在搜索相似特征时会产生错误匹配对点,对后续稀疏点云重建造成影响,本文采用随机抽样一致性算法[12-13]对匹配点进行筛选,以剔除错误匹配对。由于在计算位姿时易存在噪声干扰,在此采用光束平差法[14]进行参数优化。
SfM方法获得的三维点云具有稀疏性,采用基于面片的三维多视角立体视觉算法[15]进一步扩展,获取稠密点云的三维重建结果(图3),其中A1号植株得到2 411 949个密集点云,A2号植株得到2 657 958个密集点云,A3号植株为2 993 183个密集点云;B1号植株为2 089 776个密集点云,C1号植株为2 873 681个密集点云,D1号植株为2 067 818个密集点云。
1.2.3叶片面积计算
基于三维点云模型进行叶片面积计算,主要分为点云去噪、单个叶片分割、叶片表面网格重建、叶片面积计算。
(1)点云去噪
点云获取过程中,由于人为扰动或设备本身缺陷易产生噪声点云,使所测数据与实际物体之间存在偏差,因此,需对原始三维点云模型进行去噪与平滑,主要分为背景分离和植株去噪。对于存在大片背景点云的植株,使用Meshlab软件中的滤波器工具从背景点云中提取植株,得到去除背景和树干的完整植株叶片点云,如图4所示。
从图4中可以看出,植株叶片部分由于表面反光或叶片遮挡产生了白色噪点,难以去除。以噪点颜色与叶片点云颜色特征不同为依据去除噪点。典型的颜色空间[16]有RGB颜色空间、YUV颜色空间、HSV颜色空间,其中HSV颜色空间类似于人类感知颜色的方式,可直观表达色彩的色调、明暗,更利于颜色提取。因此,选取HSV颜色空间作为特征,提取叶片的颜色阈值创建掩膜函数,在Color Threshold可视化界面中,提取叶片颜色特征边界值[17]。通道1的阈值为[0.175,0.413],通道2的阈值为[0.164,0.829],通道3的阈值为[0.121,0.641],输出掩膜矩阵,利用掩膜矩阵生成去噪后的植株叶片光滑点云,如图5所示。去噪后,点云数量发生明显变化,其中A1号植株点云数为325 289个,A2号植株点云数为492 496个,A3号植株点云数为585 366个;B1号植株点云数为536 566个,C1号植株点云数为129 783个,D1号植株点云数为1 058 048个。
(2)单个叶片分割
根据叶片在三维空间中的分布情况,任意两片叶片之间存在空隙,为单个叶片分割提供了前提条件。为减少运算时间,先对叶片点云按比例采样再分割。本文采用FCM聚类[18]进行单个叶片分割,通过隶属度矩阵和聚类中心把x个样本点划分为C个不同的类别,即利用拉格朗日乘数法最小化目标函数,进而得到聚类中心和隶属度矩阵的迭代公式,不断更新聚类中心和隶属度矩阵,直到满足迭代终止条件输出聚类结果,叶片点云聚类分割结果如图6所示。
(3)叶片表面网格重建
由于植物叶片表面存在不平整现象,直接使用离散点云求取面积,会造成最终结果不准确,为解决该问题,本文采用Delaunay三角网格剖分[19-20]重建叶片表面网格模型,以有效识别曲面边界,完成表面网格重建。
Delaunay三角网格剖分基本步骤[21]为:①首先构造一个包含所有点的超级三角形。②再插入散点,根据空圆特性找出其外接圆包含插入点的三角形,删除影响三角形的公共边。③循环执行步骤②,直到没有多余的散点能够形成三角形,图形化结果如图7所示。图8为叶片表面网格重建效果图。
(4)叶片面积计算
叶片点云表面网格重建后,表面形成多个小三角形,计算所有三角形的面积总和可得出叶片的总面积。叶片点云中的各点可作为各个三角形的顶点,而各点坐标已知,以图7d中单个三角形PBC为例,根据3个顶点的坐标可确定各边边长为
(1)
(2)
(3)
式中DPB、DBC、DCP——三角形PBC的各边边长
(xB,yB,zB)——三角形顶点B的坐标
(xP,yP,zP)——三角形顶点P的坐标
(xC,yC,zC)——三角形顶点C的坐标
根据海伦公式可得该三角形的面积[22]为
(4)
其中
p=(DPB+DBC+DCP)/2
式中SPBC——三角形PBC的面积
在整个点云模型表面网格中
(5)
式中r——叶片点云表面网格重建的三角形数量
Si——第i个三角形的点云面积
S——叶片的点云面积
借鉴二维图像计算面积的方法[23],求解叶片真实面积。为与植株点云颜色区别以及减小误差,制作一黑一红两个边长为4 cm的正方形小方块作为参照物。
(6)
式中SC——参照物点云面积
Sy——叶片的实际面积
2 结果与讨论
为验证所提出叶片面积三维测量方法的有效性,进行实验分析,同时与二维图像法以及网格作图法计算面积进行对比分析。图像采集设备为iPhone 6s手机,后置摄像头为1 200万像素,光圈为f/2.2,运行内存2 GB。
二维图像法计算面积是基于所求叶片区域的图像像素数与整个图像像素数的比值等于所求叶片面积与整个图像面积的比值,再通过比例尺计算出叶片实际面积。利用PhotoShop软件得到相关区域像素数并用标尺工具测量图像与实际物体间的比例尺,计算出叶片面积[24-25]。在网格作图法实验中,要求叶片展平并按压平整,在单位为1 mm×1 mm标准的网格纸上用细笔勾画出叶片轮廓,然后统计网格个数,求和即可得叶片面积。
对比实验采用离体叶片,从植株上收割叶片,在充分按压平整的条件下进行实验。由于最小网格面积为1.00 mm2,网格数对叶片面积影响微乎其微,因此只要作图和统计过程较为精准,可将其视为真值参照。对于植株A1、A2、A3、B1、C1、D1,3种方法的叶片面积计算结果如图9所示。
四季青组内误差对比和植株组间误差对比结果分别如表2和表3所示,A组中,本文方法与网格作图法相比,3次实验的平均绝对误差为0.99 cm2,相对误差为5.96%;二维图像法与网格作图法相比,3次实验结果的平均绝对误差为1.16 cm2,相对误差为6.94%,从计算结果可知,本文方法较二维图像法准确度提高了0.98个百分点。在B1、C1、D1组中,本文方法与网格作图法相比,3次实验结果的平均绝对误差为2.74 cm2,相对误差为4.81%;二维图像法与网格作图法相比,3次实验结果的平均绝对误差为2.59 cm2,相对误差为4.38%。相较A组实验样本,B、C、D组样本叶片形状复杂度提高,但由于叶片面积的增大,本文方法与网格作图法的相对误差的平均值和二维图像法与网格作图法的相对误差的平均值都有一定程度的降低,说明本文方法和二维图像法都更适合较大的叶片面积测量。
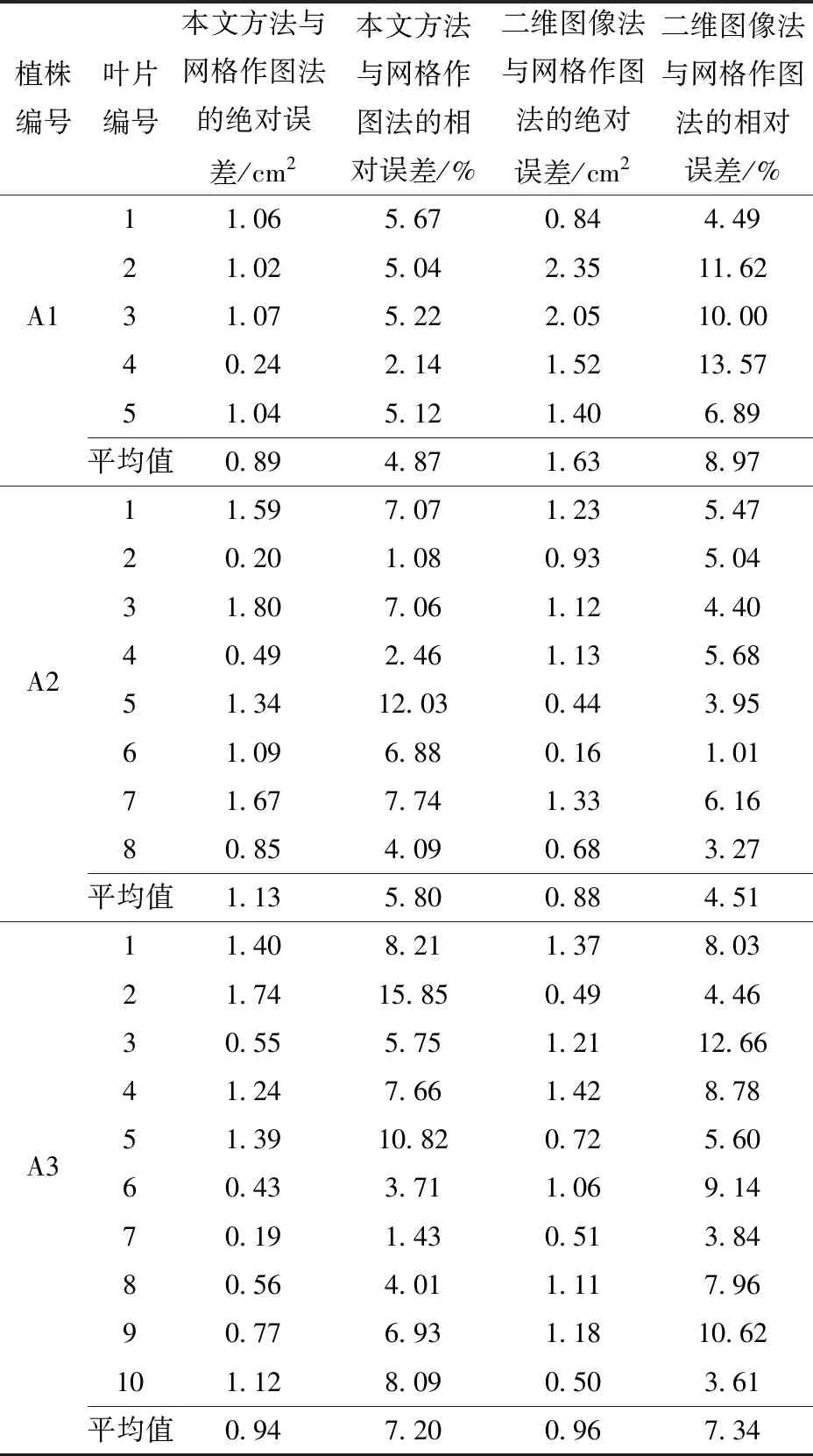
表2 四季青组内误差分析结果Tab.2 Analysis results of within error of Sijiqing group
另外,对A2、C1、D1的测量结果分析可知,本文方法误差平均值略高于二维图像法,其原因为:对于植株A2,由于底层叶片被遮挡而无法重建,叶面积误差会略微增大,但该误差在重建过程中是可预见、可处理的(为简化实验以及保证实验的真实性,本文中未做多余补全缺失点云处理);对于植株C1、D1来说,其叶片类别复杂度较高,不仅存在叶片卷曲、不平整等普通叶片的常见问题,还会出现裂口、倒刺等其他问题。二维图像法需要人工进行叶片预处理,即需要整理并按压平整等,本文方法不需要搭载复杂的系统及人工干预,简单便捷,且不会对植株造成不可逆转的伤害,具有一定的可靠性和稳定性。
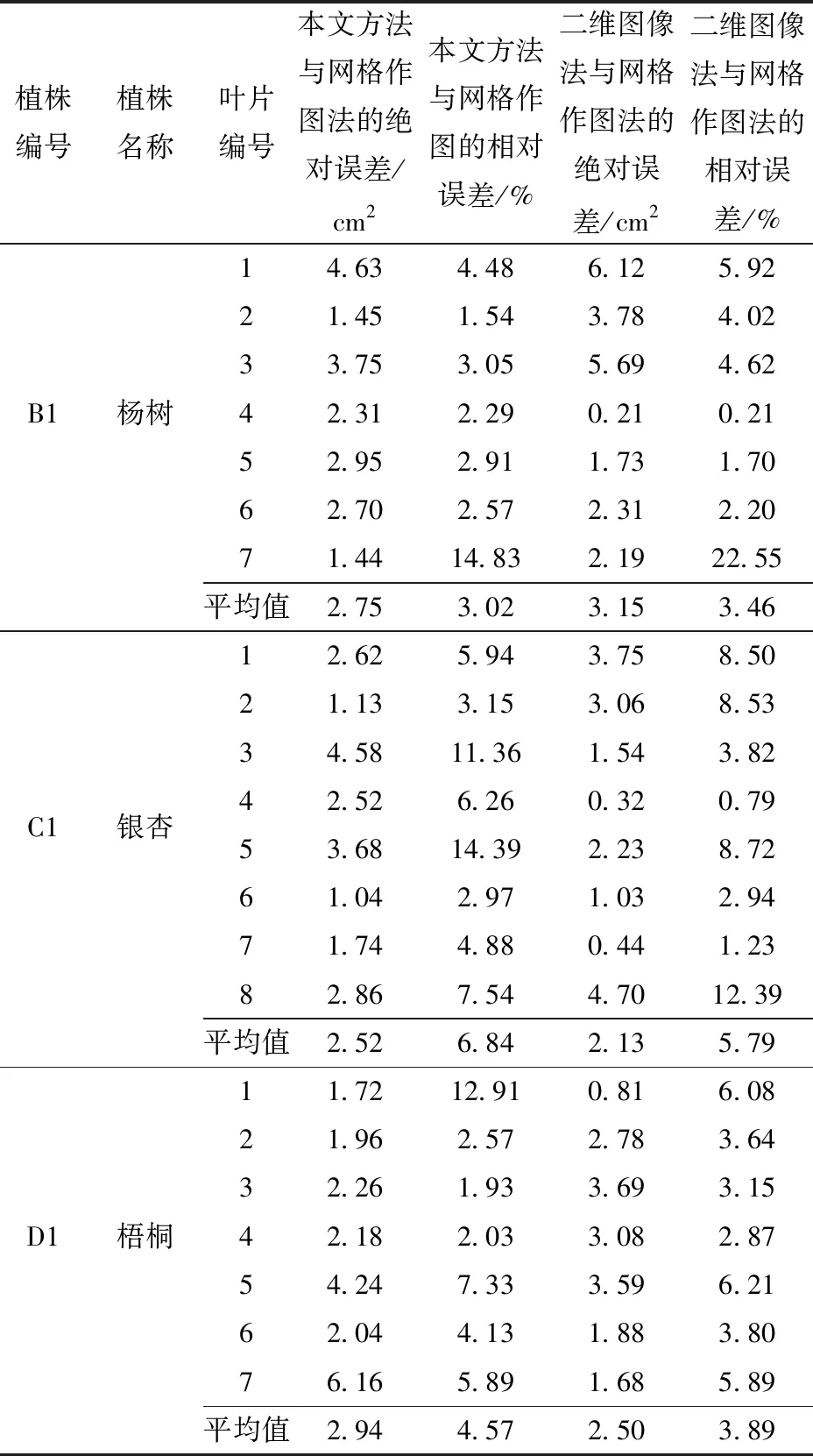
表3 组间误差分析结果Tab.3 Intergroup error analysis results
为进一步验证本文方法的有效性,选取枝叶茂密的香樟树苗,如图10a所示,在该植株中选择树叶重复率和遮盖率较高的部分作为本次验证实验的主体样本,共28片树叶,具体叶片细节如图10b所示,经过去噪处理(图10c)后,由FCM聚类分割叶片,如图10d所示。由图10d可知,叶片能被大致分割,但在个别相交部分,存在混杂情况,对于该情况采用手动删除已聚类部分后再重新聚类剩余部分,直至全部分割完成,叶片面积计算结果如图11所示。叶片误差分析见表4,本文方法与网格作图法相比,实验结果的平均绝对误差为0.64 cm2,相对误差为6.25%;二维图像法与网格作图法相比,实验结果的通过上述实验结果分析可知,除了形状复杂的叶片之外,本文方法计算所得的叶片面积比二维图像法计算所得的叶片面积精确度更高,操作更加简单、成本低廉,且具有不破坏植株的优点。从数据结果来看,相较于网格作图法,本文方法测得的叶片面积存在部分数据偏大或偏小的情况,这是由于叶片面积测定结果与点云面积关联较大。测定结果偏大原因为:由于获取点云时并非利用高精度的设备,故点云会存在微小的错位情况,植物叶片的卷曲度可能在一定程度上变大,导致点云面积增大;某些叶片产生反射或噪点颜色与叶片颜色接近,在点云去噪过程中不能完全去除,导致点云面积增大。测定结果偏小原因:叶片在按压过程中,由于叶片较软且参差不齐,叶片边缘部分存在内折无法展开,导致用二维图像法或网格作图法所测叶面积结果偏小;在相机绕植株一周时,存在某些叶片被其他叶片遮挡的情况,相机无法捕捉该部分叶片,在重建过程中该部分点云缺失,导致点云面积减小。
平均绝对误差为0.72 cm2,相对误差为7.02%,根据表4可知,相比二维图像法本文方法准确度提高了0.77个百分点。
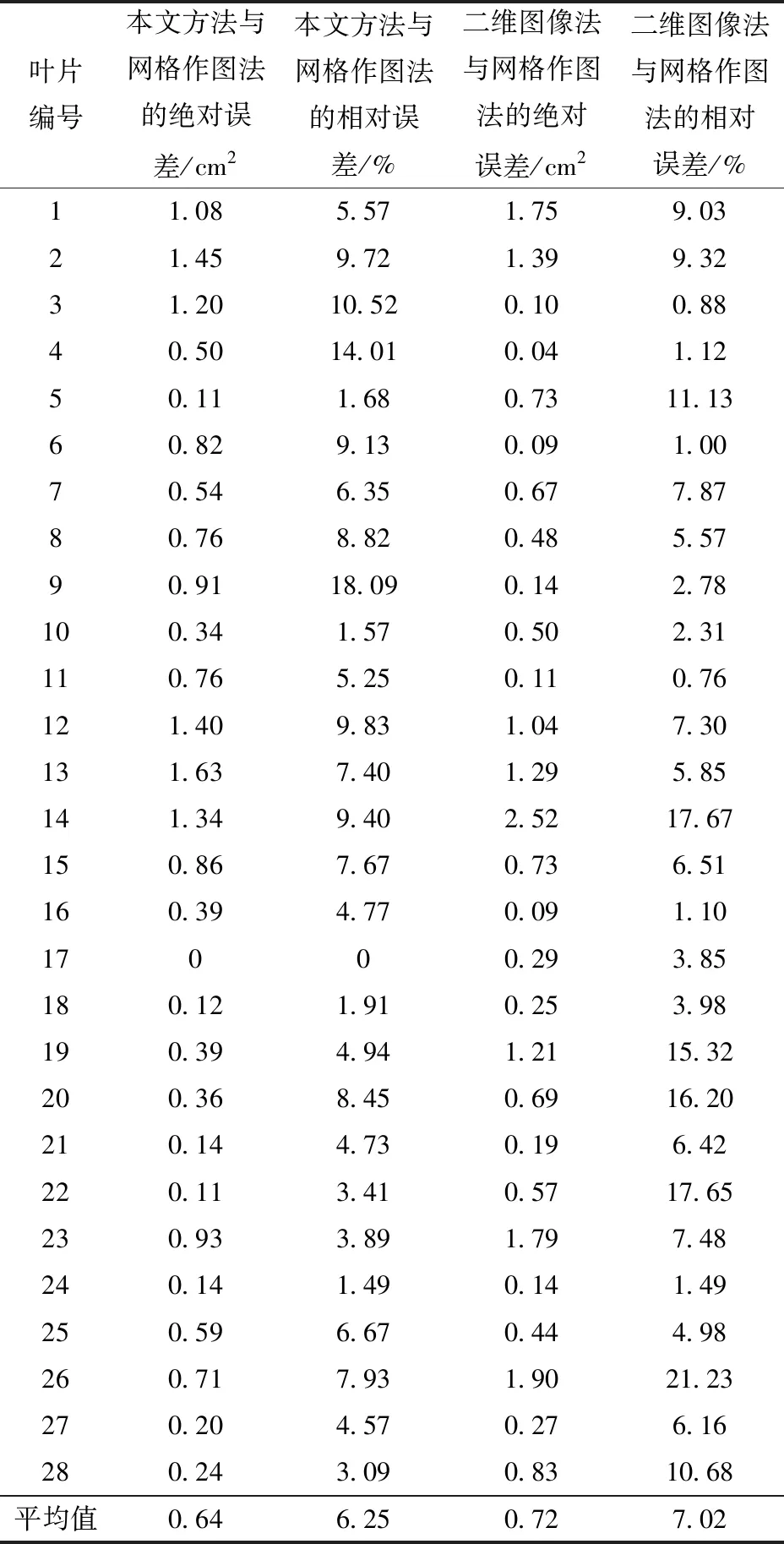
表4 叶片误差分析结果Tab.4 Blade error analysis result
3 结束语
提出了一种在普通环境下利用智能手机相机和运动恢复结构获取三维点云的叶面积测量方法。以四季青、杨树、银杏、梧桐植株为实验对象进行了叶片面积测量,结果表明,在叶片重叠率和复杂性角度上,本文方法面积测量的平均相对误差分别为6.25%和4.81%。本文方法更适合于处理普通形状叶片,对于普通重叠率的整个植株叶片总面积测量结果比采用二维图像法的面积测量结果精确度提高0.98个百分点,对重叠率高的叶片提高了0.77个百分点。相较二维图像法和网格作图法而言,本文方法测量工作量大大降低,成本低,可操作性强,且不会对植物造成不可逆转的伤害,能够满足实际农业生产的测量需要。
