基于CSA-SIM-LSSVM的不同时间尺度参考作物蒸散发估算研究
2021-05-18王文川赵钊张磊
王文川, 赵钊, 张磊
(1.华北水利水电大学 水资源学院,河南 郑州 450046; 2.华北水利水电大学 水利学院,河南 郑州 450046)
自2012年我国实行最严格水资源管理制度以来,如何更高效地管理、利用好水资源一直是热门问题[1]。农业用水作为用水大户,其中针对作物进行需水量精准把握是决策者的必修功课。参考作物蒸散发(Reference Evapotranspiration,ET0)是计算作物需水量的关键环节,以往该值的估算大多依赖于各种基于实验的经验公式,如Blaney-Criddle公式[2]、Irmak-Allen公式[3]、Ritchie模型[4]、Priestley-Taylor公式[5]和Penman-Monteith公式[6]。其中的Penman-Monteith公式在全球范围内得到了广泛应用,且能在不同类型地区取得较好的计算效果[7]。但该公式需要较为全面的气象参数,而相关参数在有些区域是难以获得的[8]。随着人工智能和机器学习的发展,诸多新型技术得以在ET0估算上应用并取得了一定的效果。侯志强等[9]将ET0视作为各种气象因素影响下的复杂非线性问题,利用最小二乘支持向量机(Least Square SVM,LSSVM)对河套地区日ET0进行了模拟研究。该研究显示,在同等输入气象因子条件下,LSSVM的表现好于传统的Priestley-Taylor公式和Hargreaves公式。但是LSSVM模型的性能高度依赖其控制参数,在此基础上,一些智能优化算法展示了较高的客观性和效率。鞠彬和王嘉毅[10]利用粒子群算法(Particle Swarm Optimization,PSO)与LSSVM耦合进行月尺度ET0的预测模拟,但是在全气象要素输入情况下其精度仍然不高,平均相对误差高达13.52%。张育斌等[11]则采用耦合模拟退火算法(Coupled Simulated Annealing,CSA)优化LSSVM模型参数形成CSA-LSSVM模型,该模型的日尺度ET0预测的平均均方根误差RMSE为0.39 mm/d,精度得到较高提升。与此同时,其他类型的机器学习模型诸如极限学习机[12]、极限梯度提升算法[13]、高斯回归过程[14]等在ET0估算模拟领域也取得了一定的研究成果。
综合上述研究成果可以看出,模型自身的结构对ET0模拟精度起着基础性作用,对于模型参数的调整也是至关重要的一步。上述文献中关于模型调整参数全局优化的PSO算法和CSA算法能力有限,十分有必要进一步平衡算法以提高全局寻优和局部挖掘能力。鉴于此,本文采用LSSVM为基础预报模型,从优化算法的角度首先采用CSA算法为全局探索算法,利用多个起始点进入第一阶段的寻优确定多个可能极值点,第二阶段再利用擅长局部挖掘的单纯形法进一步提供更可靠的候选解。此外,针对日尺度和月尺度ET0估算工作的不同特性,尝试引入其他新兴技术和特殊农时知识,例如LASSO回归法筛选因子[15]、小波包分解降噪技术[16]和旬序数[17]。以此降低ET0估算对气象数据的要求和进一步提高ET0估算的模拟精度,为水资源管理的决策提供更多的方法参考。
1 基本原理
1.1 耦合模拟退火-单纯形(CSA-SIM)组合算法
1.1.1 耦合模拟退火算法
经典模拟退火算法(Simulated Annealing,SA)在寻优过程中引入了Metropolis准则,即以一定的概率接受较差目标函数值,从而避免算法掉入局部最优。伴随着温度的不断收缩,SA寻优半径逐渐减小趋于0以达到全局最优。但是,该算法在使用过程中受初始温度和温度收缩规则的影响,往往寻优精度不高。由此,Souza等提出了耦合模拟退火算法(CSA)[18]。不同于传统的模拟退火——每次只生成一个解的寻优过程,CSA在解决方案空间的探测过程中引入了多次启动初始化以提供更多的先验信息,在各个退火过程中利用一个耦合能量(代表接受概率)和温度等信息的公式实现信息的交互以提高多样性,这种改进策略在一定程度上减少了寻求全局最优过程的迭代计算量。耦合模拟退火算法主要包括搜索向量的生成和接受两个主要过程,公式表达如下:
(1)
式中:x为启动器;Ω为搜索域;θ为当前超参数的集合;n为CSA初始启动器数量;rand为[0,1]均匀分布上产生的随机数;Tk为k时刻的温度;k为迭代次数。因此,y的分布半径会随着Tk越大而更大,反之变小,最终值也会逐渐收敛于0。本文采用下式的温度更新规则:
(2)
CSA算法可看作为多个SA算法的耦合算法。对最小化问题而言,单个启动器的候选解的接受概率函数令为A(xi→yi),即:
(3)
式中:xi为当前状态;yi为新状态;Tac为当前接受温度,其更新规则参阅文献[18];E指整个系统的能量。
利用Boltzmann参数求解仅有两个状态(i=1、2)的系统在第i个状态的概率Pi:
(4)
式中:kB为Boltzmann常数;Ei为i状态下当前系统的能量值;T为i状态下的温度;Z为当前系统所有状态的能量和。
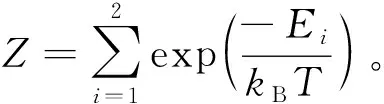
(5)
在状态yi和温度T已给定的情况下,状态yi被接受的概率值由式(6)近似表示。为了实现耦合模拟退火,先初始化一个多状态系统,x为状态的集合,xi为当前的第i个状态,yti为第i个当前状态将要转移的新状态。设x∈(x1,x2,…,xn),式(3)转换为式(6):
A(xi→yti)=
(6)
此时,当前状态x∈(x1,x2,…,xn)对应新状态yt∈(yt1,yt2,…,ytn)的接受概率为A(x→yt)∈[A(x1→yt1),A(x2→yt2),…,A(xn→ytn)]。状态集合x内各个状态接受对应的转移状态yt的概率,除了考虑自身外,还要考虑其它状态的耦合。特殊情况下,当状态总数n=1时,方法将退化为传统的模拟退火求解问题。因此,CSA在接受精度高的解的同时能够接受拟合较差的候选解,并以此实现信息的共享,促进增强单启动SA算法。详细的求解过程可参阅文献[18]。
1.1.2 单纯形法
单纯形算法(Simplex Algorithm)是Nelder和Mead提出的一种擅长局部优化的方法[19]。单纯形是具有n+1个顶点的几何图形,算法步骤主要有初始、准备、反射、延伸、收缩、棱长减半和程序出口。对于给定经度ε的最小化问题,单纯形法过程简便,详细的求解步骤可参阅文献[19]。
1.1.3 耦合模拟退火—单纯形优化算法
首先利用耦合模拟退火算法进行全局寻优以获得质量较好的数个局部最优点,再将其结果当作单纯形优化的初始点进行局部挖掘,进而减少计算资源,提高效率。
1.2 最小二乘支持向量机(LSSVM)
最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)是一种在经典机器学习模型——支持向量机基础上发展的改进算法[20]。原始支持向量机(Support Vector Machine,SVM)可用来解决分类和回归问题[21]。对于回归问题,SVM的基本思想是通过核函数把低维空间中的非线性问题变换到高维特征空间中的线性回归,对应地在这个高维特征空间中寻求一个最优超平面或最优超曲面来寻求问题的解。假设某训练样本的集合为(xi,yi),i=1、2、…、N;xi∈RM,yi∈R,其中xi为输入向量,yi为对应xi的输出向量,N为样本个数,M为维数。设经过变换后的非线性回归函数为f(x)=
(7)
式中:γ为正则化参数;δi为第i个松驰变量。
引入拉格朗日因子αi和KKT条件, Lagrange函数L可写为:
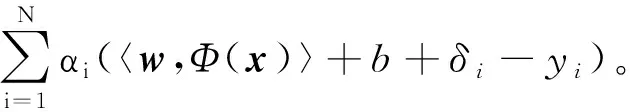
(8)
分别对w、b、δ和α求偏微分可得:
(9)
消去(9)中的w和δ,可得:
(10)
式中:E=(1,1,…,1)T;Z=[Φ(x1),Φ(x2),…,Φ(xN)]T;A=(α1,α2,…,αN)T;Y=(y1,y2,…,yN)T;I为单位矩阵。经高维空间映射后计算量巨大,选用满足Mercer条件的核函数K(x,xi)=<Φ(x),Φ(xi)>,那么LSSVM模型的回归方程最终确定为:
(11)
由以上可以看出,合适的核函数是保障LSSVM模型的预测精度的必要条件。常用的核函数有:
(12)
式中:g、r、d均为核函数的参数,即需要调整的参数。
一般而言,线性核函数适用于线性可分的情况,比较适合特征数量很多,与样本数相差不大的情形;多项式核函数和径向基核函数均能将低维问题映射到高维特征空间,由前述公式不难看出,多项式核函数参数更多。对于参考作物蒸散发预测问题,特征数与样本数均不大,综合考虑,本文采用径向基核函数。
确定了核函数之后,由公式(11)可知LSSVM模型最终的回归方程与正则化参数γ和核函数参数g有关,也即算法欲优化的目标函数为:
error=f(x|γ,g)。
(13)
式中error为在参考作物蒸散发预测模拟问题中的各种误差形式。由公式(13)知,在确定的输入训练矩阵x下,优化算法的目的在于寻找合适的γ和g使得error最小。
2 CSA-SIM-LSSVM估算模型实现
按照上述的CSA-SIM算法以及LSSVM模型的原理,本文提出的CSA-SIM-LSSVM模型旨在:搜寻一组最优的向量(γ,g),在模型训练过程中采用十折交叉检验法[22],使得模型训练代表误差的目标函数值最小。针对确定的实验样本、输入因子集合和输出,CSA-SIM-LSSVM的实现流程如图1所示。
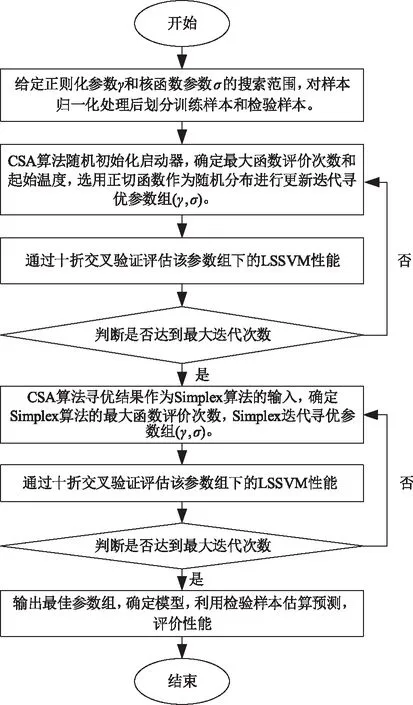
图1 CSA-SIM-LSSVM模型流程图
3 应用实例
3.1 研究区域和数据特征
研究区域为华北平原(112°30′E~119°30′E,34°46′N~40°25′N),北起燕山,南至黄河,东临渤海,西以太行山为界,南北方向长约630 km,东西方向长约640 km,总面积约为13.92 km2。该地区是我国重要的农业基地,主要种植作物有小麦、玉米、棉花等。多年平均降水量为539.0 mm,降水季节分布不均匀,多集中在7—9 月份,且年际变化较大;年平均气温约为13.0 ℃;年平均日照时数约为2 430 h;年平均风速可达2.27 m/s。选取平原外围4个不同方位的气象站点作为研究对象(如图2所示),分别是密云(116°52′E,40°23′N)、灵寿(114°23′E,38°18′N)、延津(114°11′E,35°9′N)和沾化(118°7′E,37°41′N)。这4个站点具有较好的代表性,包含有1970年1月至2019年11月期间的每日气象资料,气象资料来源于中国气象局国家气象信息中心(http://data.cma.cn)地面气象资料,数据质量可靠,总体正确率接近100%。收集的日尺度常规气象因素包括相对湿度RH、日照时数n、2 m高处平均风速u2(由10 m高处平均风速换算得到)、平均气温Tmean、最高气温Tmax和最低气温Tmin,少数缺失的数据采用线性插补或往年同期数据进行移植,使其完整。
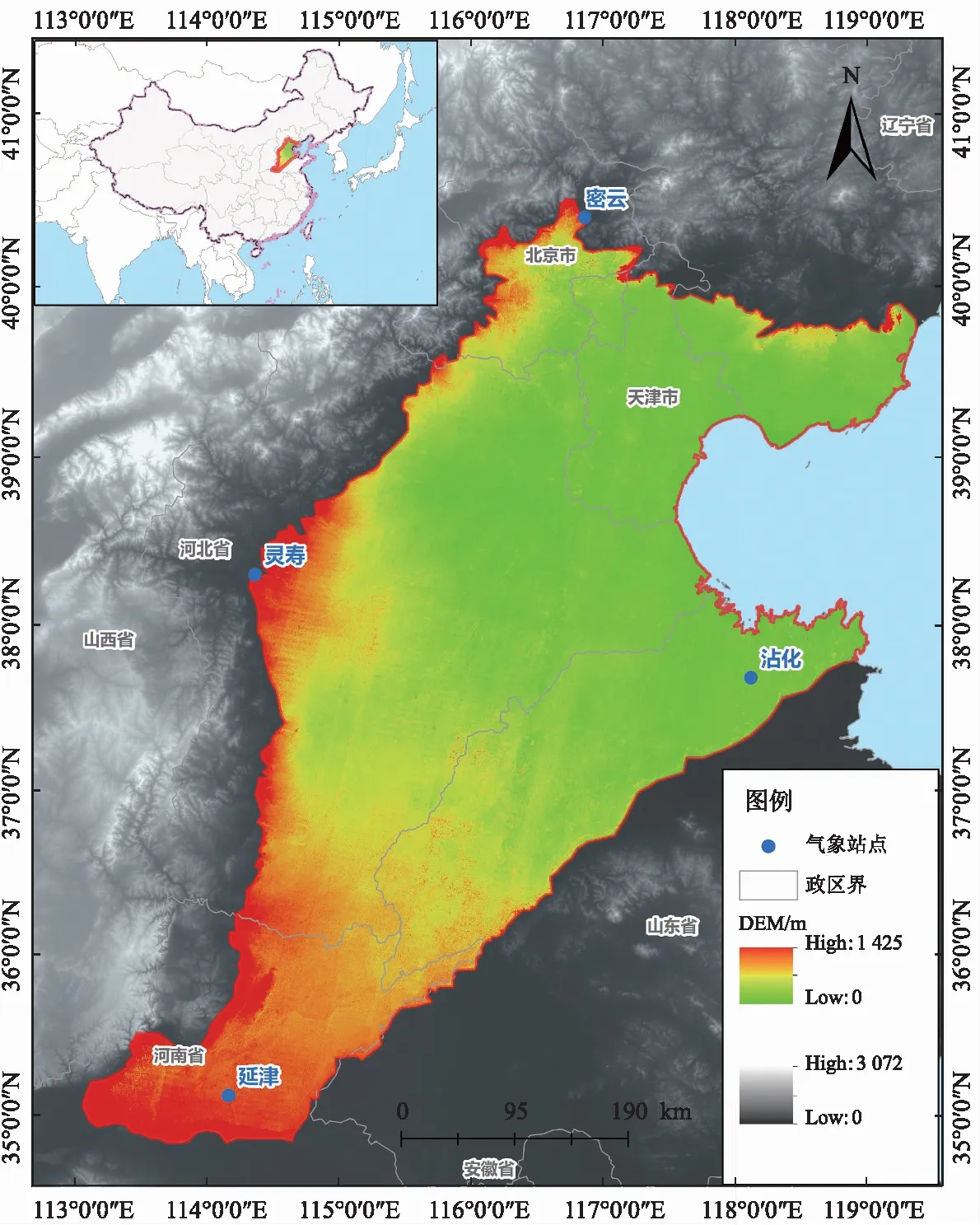
图2 研究站点分布图
3.2 研究准备
3.2.1 对照模型设置和相关参数
分别从算法和模型2个角度设置对照模型,包括PO-LSSVM模型、LSTM模型和RF模型。其中,PO算法是一种新型算法,已被相关实验证实其具有较强的竞争力[23]。LSSVM模型γ和g的上下限范围设为[e-10, e10],e为自然对数。其余相关模型算法参数设置见表1。

表1 各模型有关参数设置
3.2.2 日尺度ET0模拟
选择2015年1月份至2019年11月份(共1 795份样本)的4个气象站的日度气象数据,包括相对湿度RH、日照时数n、2 m高处平均风速u2、平均气温Tmean、最高气温Tmax和最低气温Tmin,以及旬序数共7种影响因子作为输入样本。将Penman-Monteith
公式计算ET0值作为标准值,并将样本数据的前2/3(1 197 份)作为训练样本,剩余1/3(598 份)作为检验样本。利用LASSO回归法确定不同要素组,可设置为:①全气象数据和旬序数;②RH、n、u2、Tmean和旬序数;③n、u2、Tmean和旬序数。
3.2.3 月尺度ET0模拟
以密云站为例,利用自相关系数和偏自相关系数确定前期ET0序列对当前时间ET0的影响程度。图3给出了原始月度ET0序列和8个基于db4小波函数的小波包分解子序列,8个子序列的直接叠加等于原始序列。
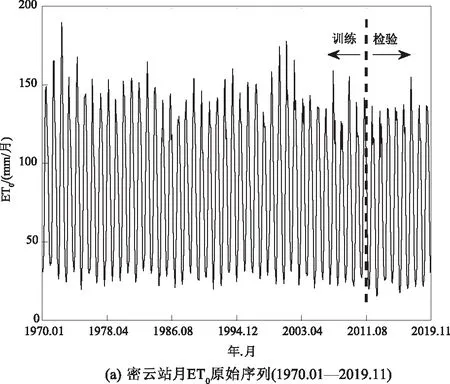

图3 密云站ET0序列及其基于小波包分解的结果
每个子序列将利用提出的CSA-SIM-LSSVM模型独立运行10次取平均值,8个子序列分别预报完毕后直接叠加得到预报结果。本次模型采用1970.01—2019.12序列末尾的100个月ET0作为检验样本,训练样本由总样本数和延迟预报月数确定。
3.2.4 评价标准
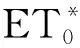
(14)
(15)
(16)
3.3 日尺度ET0估算结果对比及分析
以FAO Penman-Monteith公式为标准,按照3种不同影响因子输入组合,为减小随机性对本次研究的影响,对本节涉及的4种模型进行10次独立运行输出平均检验估算结果,记录带有模型优化过程的CSA-SIM-LSSVM模型、PO-LSSVM模型及LSTM模型的平均运行时间。3个模型的平均运行时间分别为9.16、25.85、14.99 s。4个站点上的相关平均评价结果见表2。从表2中可以得到以下结论:
1)从整体表现看,各个模型检验期的表现相比训练期绝大多数有略微的下降,总的来看,没有出现“过拟合”现象。
2)从不同类型模型之间来看,CSA-SIM-LSSVM模型表现最好,LSTM模型次之,RF模型表现最差。从算法角度进行对比,PO算法虽然更加新颖,但是本次研究证明其在优化LSSVM模型参数问题上相对于组合优化算法CSA-SIM较弱,不仅直观上表现较差,而且运行时间更长,效率较低。
3)从影响因子组合来看,CSA-SIM-LSSVM模型、PO-LSSVM模型及LSTM模型的表现从好到差为因子组合①>因子组合②>因子组合③。但值得注意的是,对于RF模型,表现次序则为因子组合②>因子组合①>因子组合③。基于CSA-SIM-LSSVM模型,LASSO回归法剔除系数为0或影响程度极低项后误差增加不明显,相较而言可缩短模型训练时间。对于LSSVM模型和LSTM模型整体而言,加入“旬序数”这一具有农业指导意义的因子项是有效合理的。
4)从其他文献提出模型的日尺度ET0模拟结果来看:张育斌等提出的CSA-LSSVM模型的误差为RMSE=0.39 mm/d[11];陈晟提出的基于多气象特征融合的RF模型的误差为RMSE=0.17 mm/d[17];邢立文等利用LSTM对华北地区ET0模拟的日度平均误差为RMSE=2.753 mm/d[24]。相比较而言,本文提出的CSA-SIM-LSSVM模型在前两种要素组合下的平均误差RMSE仅为0.061 mm/d,体现了该模型的优越性。

表2 各模型日度ET0平均拟合与检验结果评价
3.4 月尺度ET0估算结果及分析
图4给出了基于小波包分解的CSA-SIM-LSSVM(WPD-CSA-SIM-LSSVM)模型在4个站点上测试样本的预报结果曲线图,用圆圈表示Penman-Monteith公式计算值,模型的预测结果用星号表示。整体上4个站点的预报结果较为可靠,模型很好地捕捉了月ET0序列的局部变化趋势,在4个站点的ET0突变处、“双峰”处均能提供较准确的预报值。
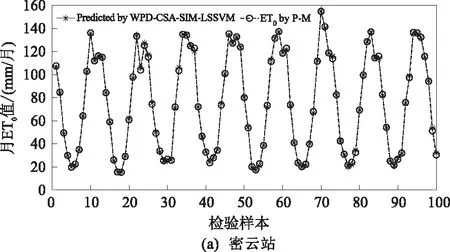

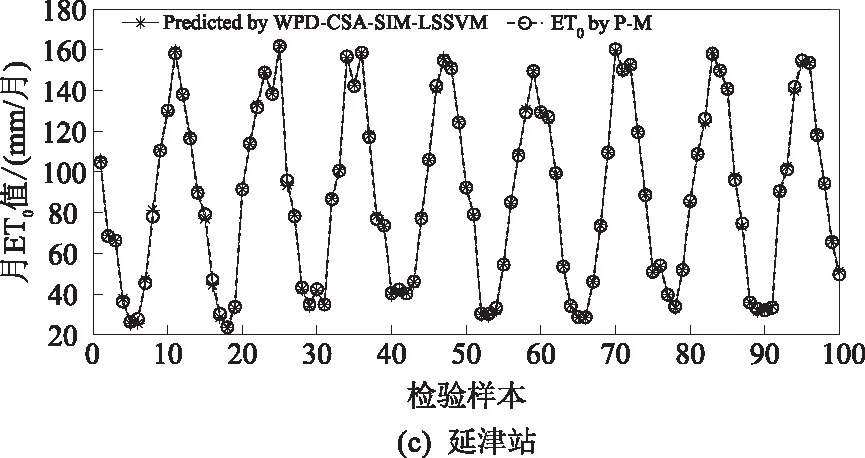

图4 各站点测试样本预报结果
表3记录了WPD-CSA-SIM-LSSVM模型在4个站点上检验与测试的平均评价结果。与其他文献提出模型的月尺度ET0模拟结果对比来看:侯志强等对于河套地区临河气象站的测试误差为MRE=11.69%[9];鞠彬等对于哈巴河气象站的模拟最小误差为MRE=13.52%[10];邢立文等利用LSTM对华北地区ET0模拟的月度平均误差为RMSE=1.460 mm/d[24]。本文提出的WPD-CSA-SIM-LSSVM模型月度模拟平均误差MRE=1.13%,RMSE=0.028 mm/d,进一步体现了提出模型的优越性。

表3 各模型月度ET0平均拟合与检验结果评价
4 结论
利用耦合退火算法的全局寻优能力,配合单纯形法良好的局部挖掘能力,并利用两者耦合算法进行LSSVM模型的参数寻优以进行华北平原的日尺度和月尺度ET0的预测估算。评价结果显示,提出的CSA-SIM-LSSVM模型在日尺度ET0估算上的表现明显好于其他对照模型,展示了其提出的合理性。配合小波包分解技术,后续月尺度ET0的预报估算进一步展示了其可行性。本文提出的CSA-SIM-LSSVM模型具有较好的模拟效果,可为实际生产工作提供参考。
