二钼酸铵母液循环中钾的数模研究与浅析
2021-05-17郝绍鹏
郝绍鹏
(金堆城钼业股份有限公司化学分公司,陕西 渭南 714000)
0 引 言
杂质钾的含量严重影响钼产品的性能,如在金属制品中影响合金的物理性能,在高温电光源原件中气化后粘结导致原件污损或腐蚀[1]。从钼产品的加工过程分析,用钼焙砂加工二钼酸铵的生产过程,是钼产业链降钾的重要环节[2]。目前国内的二钼酸铵湿法工艺,普遍采用母液循环工艺,即将蒸发结晶后剩余的母液返回氨浸工序,以减少钼金属的损失,提高金属回收率并降低运营成本[3]。在此过程中,包括钾在内的杂质也随母液的循环而返回到前端工艺,在生产体系中循环和富集。
与不使用母液循环的工艺相比,母液循环使钾的流向趋于复杂,由单向去除的过程,变为带有局部富集的总体去除过程。单向的生产过程中,投入原料的钾量直接决定本次产品钾含量,蒸发母液带走的钾量越大越有利于产品中钾含量的减少。母液循环生产过程,母液带走的钾量返回前端并最终回到蒸发环节,同时也把每次投入原料的钾量与最后一次产品的钾含量联系起来。面对钾流向分布的改变,有必要进行产品中钾含量的计算研究,探索关系式中的内在联系,补充和完善生产数据统计中分析出的实际结果。初步研究产品中钾含量的计算方式,有助于明确除杂规律、原料影响规律,也有益于探索产品钾含量控制的宏观方向和生产运营的宏观调控。
1 母液循环工艺中钾的流向梳理
1.1 钾的循环流程
二钼酸铵生产中,原料三氧化钼经过预处理、氨浸、净化、过滤等分离程序后进行蒸发结晶,结晶母液返回氨浸工序重新使用,预处理废水、氨浸渣等排出生产体系。二钼酸铵生产流程见图1。
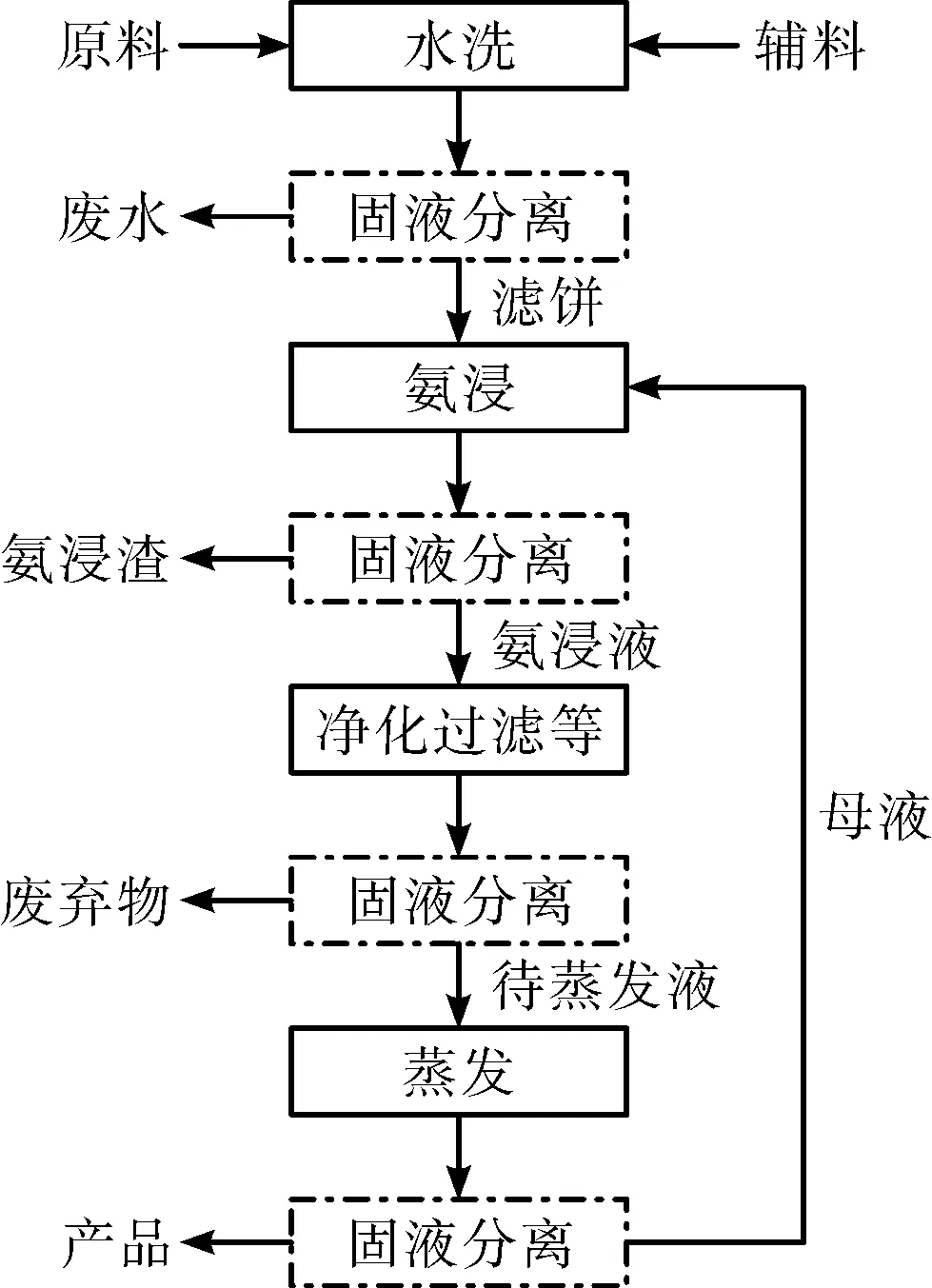
图1 母液循环生产二钼酸铵流程
二钼酸铵产品中的钾由原料带入,存在于体系中的液相和固相,不进入气相[4]。部分钾随废水、废渣和产品排出生产体系,其余的钾在体系中循环,且循环集中在氨浸及其后续的生产过程中。
1.2 钾流向分布规律浅析
根据钾的循环流程,钾流向的总体规律是在所有固液分离环节均会出现分流。根据物质守恒,每个分流环节的钾量分配规律虽然不同,但任一支流的钾量必然不大于分流前的钾量;根据生产实践,每个单一分流环节的规律或许不能准确描述,但支流的钾量随分流前钾量的增大而增大。
由于工业控制、检测精度以及数据分析工具的限制,各环节的分流分配规律一般拟合成一次函数曲线和一次函数关系式;在实际应用中,一般简化为比例关系[5]。
2 数学建模
2.1 钾流向分布抽象为数学模型
所有含钾的物料如原料、氨浸液、渣、母液、产品等,均抽象为钾量;所有工序如预处理、氨浸、蒸发等,抽象为加入物料的钾量之和;所有涉及钾分流的分离过程,假定其分流分配规律不随钾量增减而改变,即计算规则不变,将分流分配规律抽象为函数,以分离前钾量为自变量,分离后某一支流的钾量为因变量,如氨浸工序中钾量为x,固液分离后的溶液中的钾量为y,则有y=f(x)。任一固液分离的分流分配规律为一次函数关系时f(x)=kx+b,分配规律为二次函数关系时f(x)=ax2+bx+c,分配规律为对数关系时f(x)=lnx,以此类推。
2.2 数学模型优化
根据上述模型,对各环节分别立式:滤饼钾量=f1(原料钾量),氨浸液钾量=f2(氨浸钾量),待蒸发液钾量=f3(氨浸液钾量),母液钾量=f4(待蒸发液钾量)。母液循环所导致的氨浸钾量的变化,对于氨浸钾至氨浸液的钾分配规律,仅是自变量的变化,分配规律即运算规则不变亦即f2函数不变,故可将上述各关系依次带入得:母液钾量=f4(f3(f2(滤饼钾量)))。
根据函数的传统定义,可将嵌套函数的运算规则整合[6],即有:母液钾量=f(滤饼钾量),其中函数f为f2、f3、f4嵌套运算后所得的新函数,其现实意义是以滤饼钾量为自变量,以母液钾量为因变量,在变化过程中所构成的关系式。由此可知,可将各个固液分离过程根据需要进行整合,选取关键节点进行讨论。如从氨浸至蒸发之间,可将各净化分离过程的函数整合为:待蒸发液钾量=f(氨浸钾量),亦可整合为:母液钾量=f(氨浸钾量)。
本文选取滤饼及其后物料和流程为研究对象,整合氨浸至蒸发液之间的变化关系,优化后的模型流程如图2。
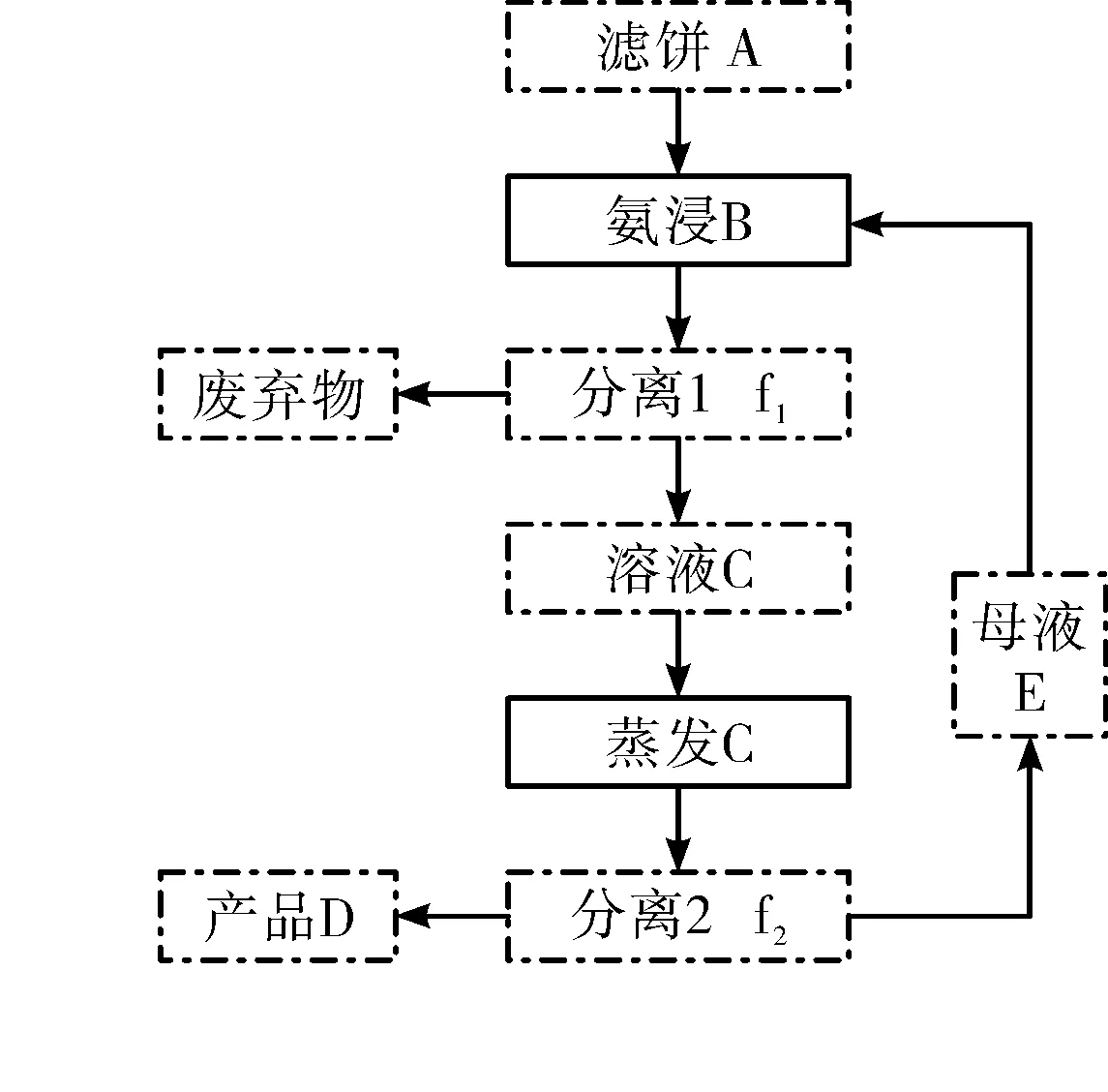
图2 核心流程及其对应符号
A、B、C、D、E分别表示滤饼钾量、氨浸钾量、溶液钾量、产品钾量、母液钾量,函数f1、f2分别表示分离1和分离2中钾在液相中的变化规律,函数f由函数f1、f2嵌套获得,表示钾在氨浸至母液过程中的变化规律。n为母液循环次数,以大写字母与下标组合代表第n次母液循环时某物料或环节的钾量,如An代表第n次母液回用时投入滤饼的钾量,A0代表母液未回用时所投入滤饼的钾量;En代表母液循环使用第n次所产生母液的钾量,E0代表母液未回用所产生母液的钾量。值得注意的是,以原料至产品的方向去描述,f1代表氨浸至待蒸发液过程中钾的残留规律,f2代表浓缩结晶过程中钾的去除规律。
2.3 函数的简化
(1)将钾分流规律浅析的结论抽象为函数表达,支流钾量随分流前钾量增大而增大,即限定了f(x)在x≥0时单调递增;(2)支流钾量不大于分流前钾量,即限定了f(x)≤x(x≥0),即函数y=f(x)的图像在第一象限内始终在直线y=x下方。(3)另外,考虑极端情况,分流前钾量可以为0,则x取值范围包含0;此时支流钾量必然为0,即x=0时,y=f(0)=0,即函数图像经过直角坐标系原点。
根据上述3个函数条件,一般函数图像在第一象限上的直观描述为:该函数图像为与x轴夹角小于等于45°的直线;或为“凸”型逐渐上扬的曲线,且其任意一点上的切线与x轴的夹角小于45°。其代数表达为:x≥0时f(x)单调递增,且f′(x)≤1。其图像具有共同特征:x=0时,图像切线斜率最大,但不超过1;0≤x≤1时,图像曲度较大;x>1时,图像近似直线,且近似后所得直线的斜率k∈(0,1)。

图3 函数示意图
在生产实践中,检测误差一般在数量级内正负5个单位,所以1个单位以内的变化规律对总体研究的影响及其微弱。取x>1时图像的近似直线作为计算基础,将难以准确描述的复杂函数简化成一次函数或比例关系,精度几乎不受影响,计算难度大大下降。对于有可能存在的更复杂的曲线,如斜波纹形式的曲线,由上述3个条件限制,其总体趋势仍然可以近似为直线。
这说明在生产实践中选择使用比例描述钾流向的分布,在客观上具有一定的科学性。本文以一次函数为基础进行关系式整理,以比例关系为基础展开主要讨论。
3 关系式整理
3.1 计算原理
根据钾的流向模型可知:初始投入即无母液循环时B=A,有母液循环时B=A+E,C=f1(B),E=f2(C)=f2(f1(B))=f(B),D=C-f2(C)=f1(B)-f(B)。以此计算规律为原则,按照母液循环顺序逐次计算B、E的值,并代入下一轮,利用数学归纳推导出Bn、En的表达式,再利用Dn=f1(Bn)-En=f1(Bn)-f(Bn)计算出Dn的表达式。
3.2 推 导
钾分流规律均为一次函数,即f1(x)=k1x+b1,f2(x)=k2x+b2,f(x)=f2(f1(x))=kx+b(k=k1k2,b=k2b1+b2);每次投入的滤饼钾量不同,以An=A+hnA(其中hn为实数)表示。如初始投入为A0=A+h0A,第一母液循环时的投入为A1=A+h1A,以此类推。
初始无母液:
B0=A0=A+h0A,
E0=f(B0)=f(A+h0A)=k(A+h0A)+b=kA+kh0A+b,
第1次母液循环:
B1=A1+E0=A+h1A+kA+kh0A+b=A(1+k)+A(h1+kh0)+b,
E1=f(B1)=A[k+k2]+A[kh1+k2h0]+b(1+k),
第2次母液循环:
B2=A2+E1=A[1+k+k2]+A[h2+kh1+k2h0]+b(1+k),
E2=f(B2)=A[k+k2+k3]+A[kh2+k2h1+k3h0]+b(1+k+k2),
……
第n次母液循环
Bn=A[1+k+k2+k3+…+kn-1+kn]+A[hn+khn-1+k2hn-2+…+kn-1h1+knh0]+b[1+k+k2+k3+…+kn-2+kn-1],
En=kA[1+k+k2+k3+…+kn-1+kn]+A[khn+k2hn-1+k3hn-2+…+knh1+kn+1h0]+b[1+k+k2+k3+…+kn-1+kn],
整理得:
由Dn=f1(Bn)-En=f1(Bn)-f(Bn)得:
(1)
4 关系式的分析、简化与近似
4.1 投入钾量浮动的分析
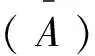
构建一个常数组成的多项式An+kAn-1+k2An-2+…+kn-1A1+knA0,将An=A+hnA代入得等式:
An+kAn-1+k2An-2+…+kn-1A1+knA0
=A(1+k+k2+…+kn-1+kn)+A(hn+khn-1+k2hn-2+…+kn-1h1+knh0)
整理得:

将此结果带入(1)式得:
(2)

(3)
(4)

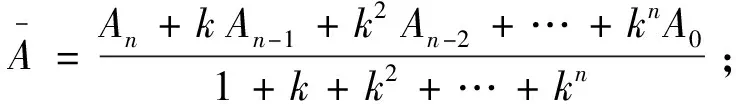
4.2 常数项的取舍
由于0 (5) (6) Dn≈(k1-k)(An+kAn-1+k2An-2+…+kn-1A1+knA0) (7) 在A值不变且除杂、蒸发等工艺水平相同时,不使用母液循环的产品钾量为:D单=(k1-k1k2)A=(k1-k)A。对比得D单=(1-k)Dn,由于0 由式(7)可知,产品钾量为两个因式的乘积。将k=k1k2代入式(7),当k2不变、历次投入钾量为常数时,第一个因式随k1的减小而减小,第二个因式同样随k1的减小而减小,即产品钾量Dn随k1的减小而减小。 当k1不变、历次投入钾量为常数时,Dn是k2的高次函数,且两因式增减性相反。从数学理论不易确定k2对Dn的影响,从生产实践中难以实现k2的线性调整,故在Excel表格中以式(7)为算法进行数据模拟计算[10]。 图4 数据模拟趋势图 表1 趋势模拟的投入钾量 此时规律与A值不变时以及不使用母液循环时的规律相同,即氨浸至待蒸发液过程中的除钾比例越大,或者蒸发母液带走的钾量越大,都有利于产品中钾量的减少。 上述权重性质结合式(6)、k=k1k2、D—k1趋势、D—k2趋势进行分析可知,k1值越小,影响产品钾量的原料最后投入次数越少,而k2不具备这种必然关系。 实践生产中,k1、k2确定,前期投料钾量和次数可统计,借助计算机软件以式(7)以及k=k1k2为算法,可以预先计算出后期投入几次、钾量多大的原料,产品钾量能达到何种水平,再结合库存原料的钾含量水平,可以判断产品钾量调整的可行性和预期水平,有助于及时对生产进行研判和科学的计划生产。这个性质和方法,可以衡量生产线对原料的适应能力,也可以估算生产线原料的供应标准,对实现产品钾含量满足客户需求的调控和研究具有指导意义。 (1)同等原料和除杂工艺水平,母液循环工艺较单向工艺的产品钾量有所增高,增高幅度取决于k值(即氨浸至待蒸发液过程钾残留率与蒸发过程钾去除率的乘积),且k值越小增幅越小。 (2)母液循环生产二钼酸铵,不改变投入产出比例的前提下,提高所有工段包括蒸发工段的除杂能力,均对降低产品钾量有益,此规律与不适用母液循环时的规律相同。 (3)相对于单向工艺,原料对产品钾量的影响,由单次投入的钾量变为历次投入钾量的加权平均值。历次投入钾量对产品钾量的影响,以投入顺序的逆向顺序递减,最后一次投料对该次产出的产品钾量影响最大。 (4)条件允许或时机适当,控制最后几次投入可以有效实现产品钾量的转变;亦可利用5.2中所述变量对加权平均值的影响,通过排列不同钾量原料的投入顺序,分段产出不同钾含量的产品。 (5)整理出的(1)至(6)式适合于用投入钾量简单计算氨浸钾量、母液钾量、产品钾量,式(7)更适合于产品钾量调控。需要特别说明的是,本文中提到的“钾量”指如质量、物质的量等为单位的数量,并非检测所得的浓度、百分比等“钾含量”,实际使用中必须根据相应的投入产出比例进行换算。 母液循环应采用尽可能少量、多次的均匀回用,其中均匀回用尤为重要。均匀回用一方面可以减少工艺过程中的变量,有利于工艺稳定,便于摸索运行规律、异常查找和工艺改进,另一方面,对产品含钾量市场适应性的调控尤为重要。 提高产品市场适应性,或提高生产线对原料钾含量的容纳范围,应注重进行待蒸发液之前各环节除钾能力的研究和优化。 作为实现上述建议的基础,生产经营控制和技术改进方面,应注重收集氨浸至待蒸发液、蒸发工段的钾量分布、变化规律,研究和明确这些过程中的微观规律。

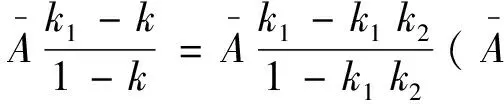

5 综合讨论
5.1 工艺系数初步讨论及不循环对比
5.2 工艺系数影响趋势



5.3 权重与工艺调节能力的探讨

6 结论与建议
6.1 结 论
6.2 建 议
